改进综合标识指数法在地下水方面的应用
——以赵川盆地为例
谢 川,李子君,王 滨,刘 禄,曹文洁
(1.河北地质大学 水资源可持续利用与开发重点实验室, 石家庄 050031; 2.吉林大学 地下水资源与环境教育部重点实验室,长春 130021)
地下水质量的综合评价是地下水资源保护和管理中不可缺少的部分,也是采取相应防御措施及制定科学有效的治理的必要前提[1]。因此,如何客观、科学合理的研究地下水的质量问题变得尤为重要。目前,常用的水质评价方法有单项指标法[2]、因子分析法[3]、BP神经网络法[4]、灰色关联法[5]、模糊综合评价法[6]等。杨永鹏等[7]在2017年采用灰色关联法对海口市地下水质量进行评价,确定了地下质量的现状情况;杨青春等[8]在2016年采用集对分析法对鄂尔多斯盆地东南部的地下水质量空间分布进行了研究。上述方法均确定了地下水水质类别,即定量的分析了地下水的质量,并未定性的表明地下水是否符合当地要求的质量标准。
徐祖信[9]提出的综合标识指数法不仅可以完整的表达单因子的水质类别,还可以定性、定量的评价出在综合水质状况。在各指标权重的计算过程中,为使评价结果更加准确、合理,本文在确定各权重的时,采用AHP和因子分析法相结合的方法,该方法不仅结合了研究区域的实际情况,而且充分考虑了采样数据的客观性。鉴于此,本文以赵川盆地2017年地下水环境调查数据为依据,采用AHP-因子分析法的综合标识指数法,对研究区的水质情况进行评价和分析。
1 基于AHP-因子分析法的综合标识指数法
1.1 评价方法
1.1.1 单因子水质标识指数评价法
单因子水质指数Pi是由一个整数、一位小数点和小数点后两位或者三位有效数字组成,形式可以表示为:
Pi=X1+X2+X3/1 000
(1)
式中:X1为某一样本中第i项水质指标的级别;X2为某一样本某一指标在类水X1标准下限值与X1类水标准上限值变化区间中所处的位置;X3为某一样本某一指标水质类别与功能区划(本文规定为Ⅲ类水)设定类别的比较结果。
(1)X1的确定。X1反映地下水中某一单一污染物的情况。评价指标根据《地下水质量标准》(GB/T14848-1993)将水质分为五类,见表1。当同一指标的不同类别具有相同的限值时,从优不从劣。

表1 地下水质量标准分级
(2)X2的确定。根据《地下水质量标准》中,一般水质指标随着水质级别的增大而逐渐增大,除水温、pH和溶解氧外,因此单因子水质标识指数Pi按溶解氧指标与非溶解氧指标分别计算。
①对于水质介于Ⅰ~Ⅳ类之间的水质指标(除了溶解氧、pH、水温等外):
(2)
②对于Ⅴ类地下水的水质指标(除了溶解氧、pH、水温等外):
(3)
(3)X3的确定。X3要通过判断得出,其主要意义是判别该单项水质类别是否劣于水环境功能区划的类别。①如果水质类别好于或达到功能区划类别时则X3=0;②如果水质类别差于功能区类别且X2不为零,则有X3=X1-fi;③如果水质类别差于功能区类别且X2为零,则有X3=X1-fi-1。fi为水环境功能区类别,当X3>9时取最大值9。
1.1.2 综合水质标识指数
综合水质标识指数法表示为:
IWQ=Y1Y2+Y3/1 000+Y4/1 000
(4)
(5)
式中:n为评价指标的个数;ωi为监测样本中第i个评价指标的权重;Pi为单因子水质标识指数;Y3某一监测样本的评价指标中,劣于水环境功能区目标的单项指标数目(小数点后第二位);Y4为监测样本综合水质类别是否劣于水环境功能区类别(小数点后第三位或小数点后的三位和四位)。
通过综合水质标识指数IWQ的整数位和小数点后的第一位(X1+X2),可以判断出监测样本综合水质级别,判断关系见表2。

表2 基于综合水质标识指数的综合水质级别判定
1.2 确定评价指标的权重
在地下水质量的评价中,各指标相对权重反映了各指标对于地下水质量好坏的贡献率的大小,从某种程度上来说,直接影响着地下水质量的评价结果。权重的计算方法有很多,而AHP-因子分析法在计算权重时,即考虑了研究区域实际情况,又结合了实际检测数据的客观存在性。因此,本文采用层次分析法和因子分析法相结合的方法计算指标的权重。
1.2.1AHP法
AHP法是由美国学者Saaty最先提出来的一种灵活、便捷的多准则的决策方法。该方法可以将人的主观依据用数量的形式表示出,使之条理化、科学化[10]。其计算过程大致分为三步:首先确定指标的标度值(见表3),并建造判断矩阵;其次,对所构建的判断矩阵进行一致性检验;最后,计算各指标的权重。

表3 判断矩阵的比例标度表
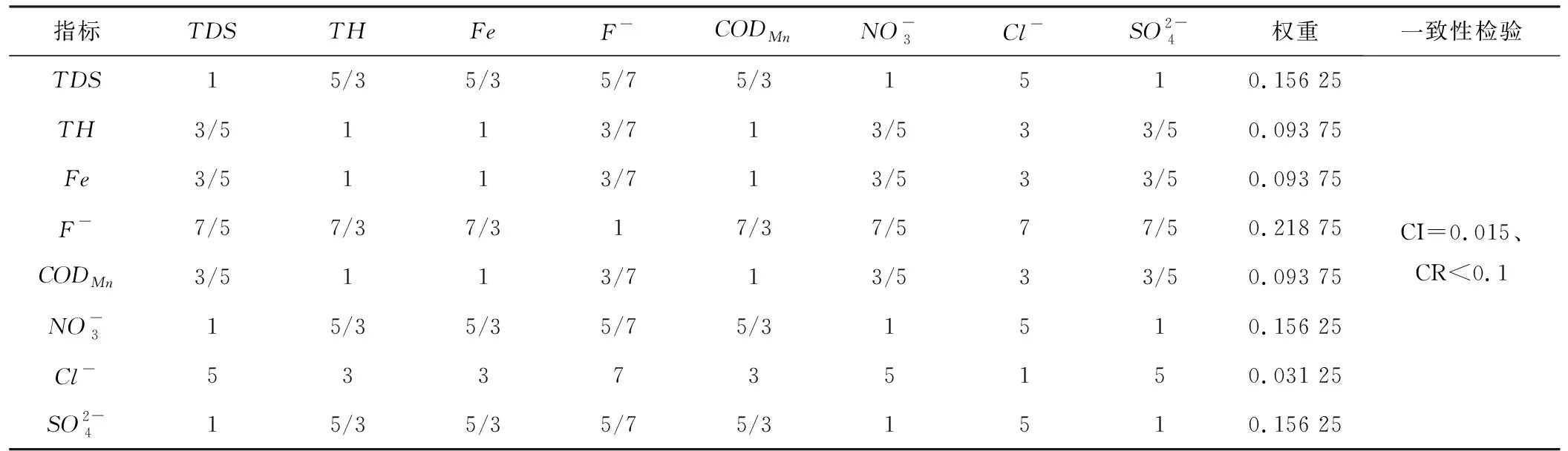
表4 层次分析法的判断矩阵
1.2.2 因子分析法
因子分析法属于多元统计分析中一种,是从资料的信息量和资源效应的角度确定地下水评价指标的权重,可以很好地克服人为的主观因素。它是通过降维的思想将大量具有相关性的指标整合为少数几个互不相关的新的指标,这几个新的指标可以表示原始数据信息的大部分信息(占原始数据信息的80%以上)[11]。
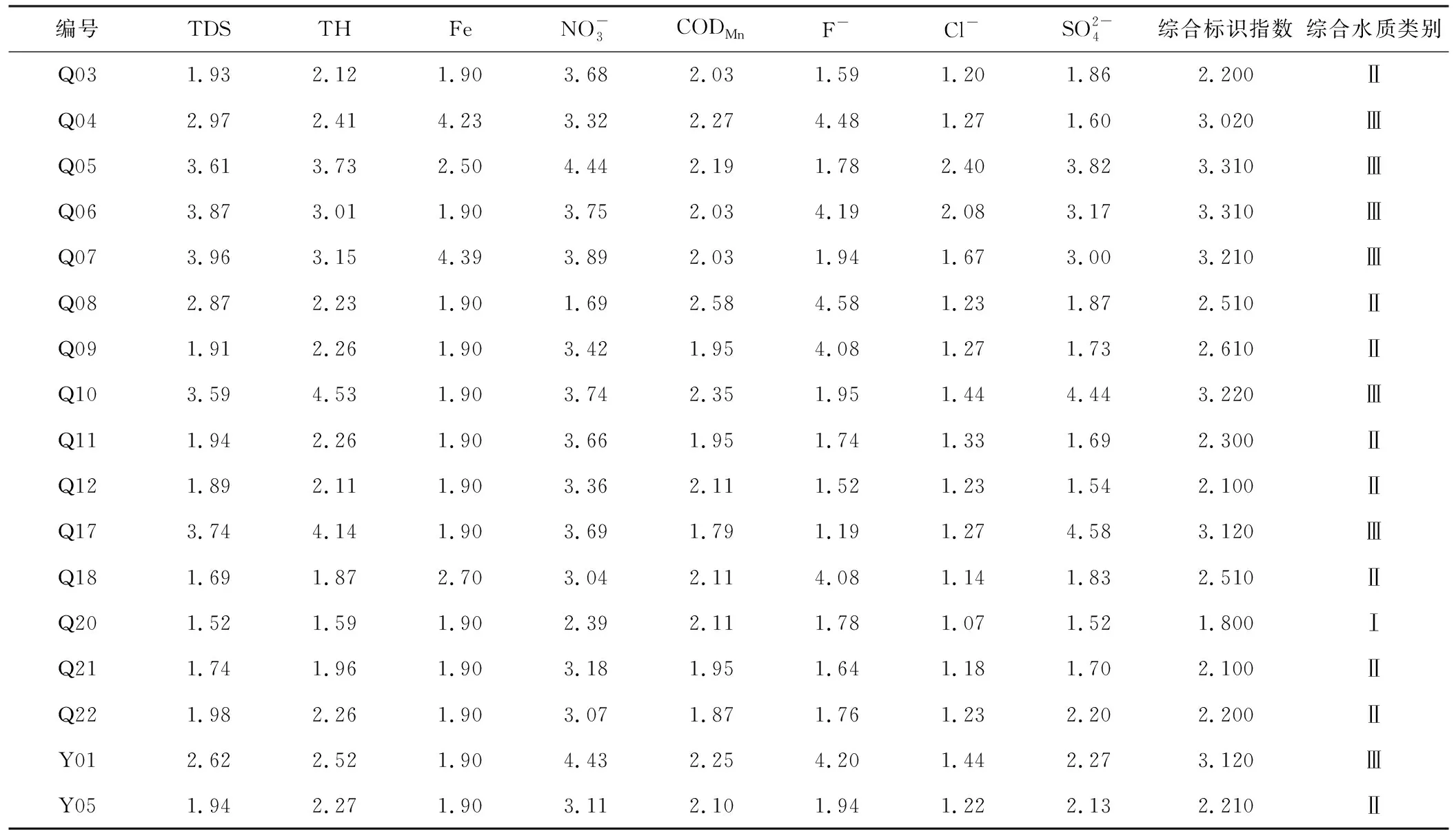
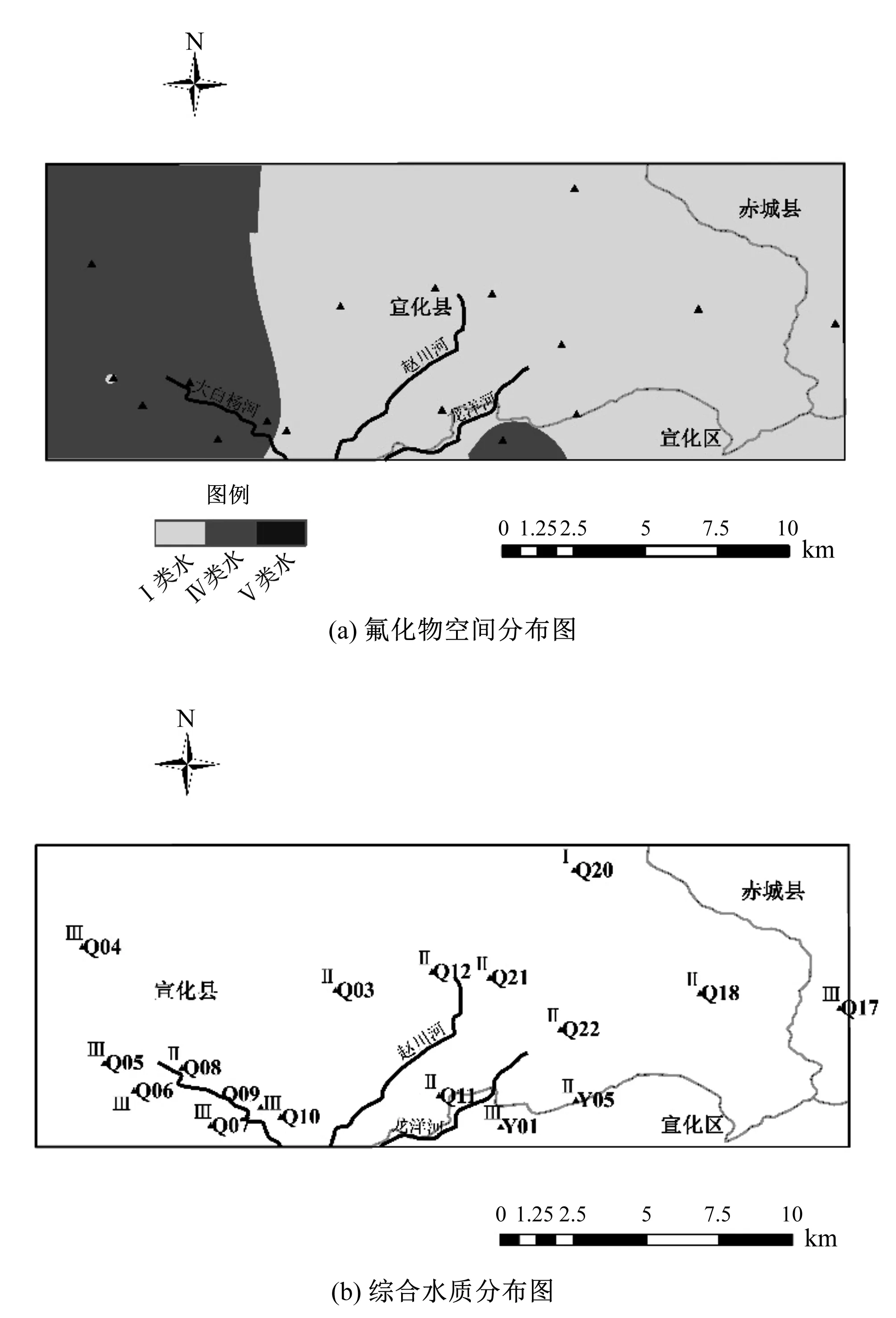
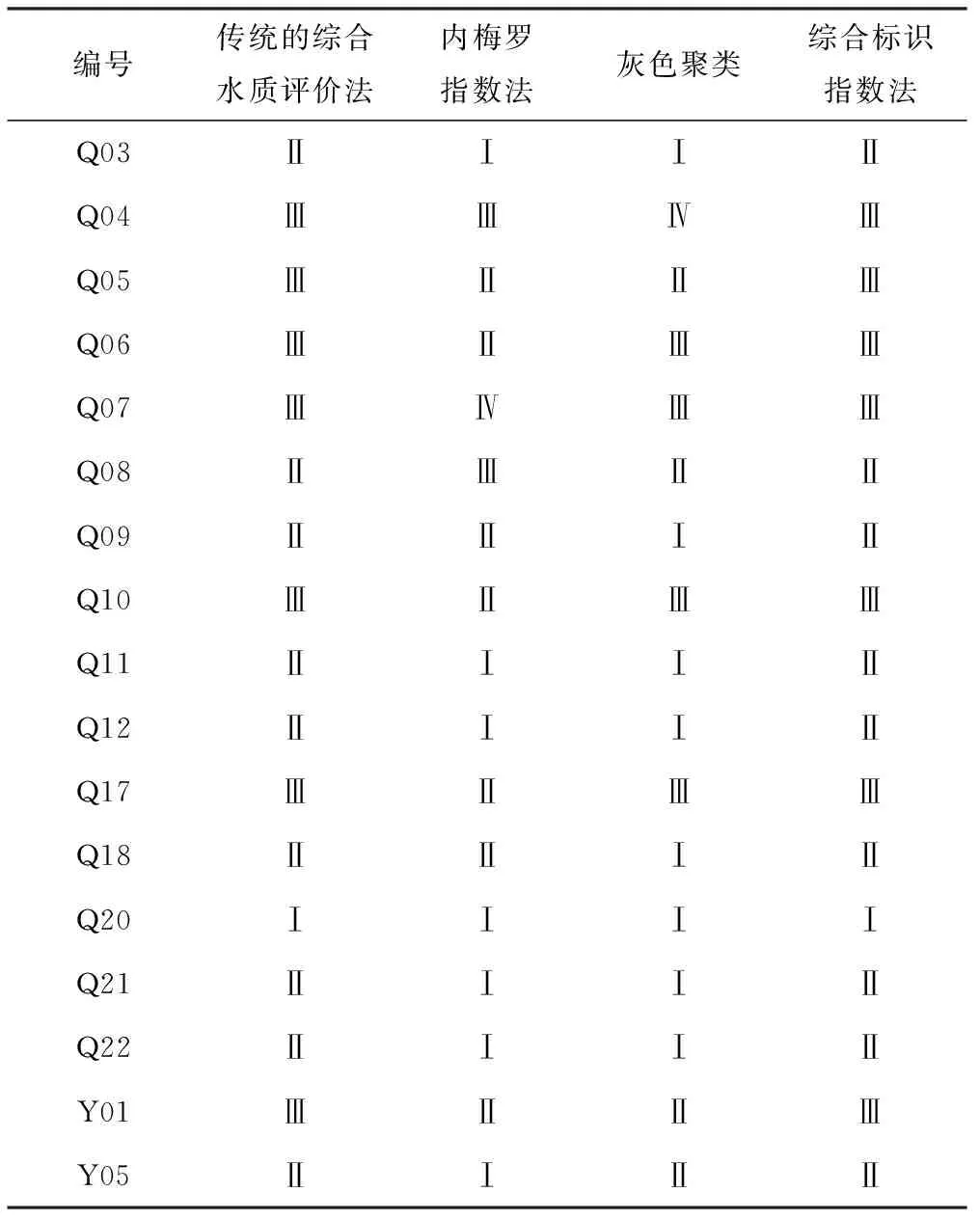
因子分析过程在SPSS软件中完成的,采用归一化矩阵T作为因子分析的输入数据。在计算过程中首先要进行KMO检验和Bartlett球型检验法以判断其是否适用于研究区域。之后,计算因子变量的方差贡献率Ei及因子得分系数矩阵β。根据因子得分系数矩阵β可建立k个主因子fi与 个评价指标(k (6) 由于新的指标fi(i=1,2,,k)包含了原始数据的大部分信息且各指标之间互补相关。因此,可以用主因子变量来描述要评价的指标L: L=E1f1+E2f2++Ekfk (7) 其中,方差贡献率Ei能直观地反映出i个因子对原始变量总方差的解释能力。其值越高,说明该因子在评价对象L中的重要程度越大。 L=E1(β11x1+β21x2++βt2xt)+ E2(β12x1+β22x2++βt2xt)++ Ek(β1kx1+β2kx2++βtkxt) (8) L=(E1β11+E2β12++Ekβ1k)x1+ (E1β21+E2β22++Ekβ2k)xt++ (E1βm1+E2βm2++Ekβmk)xm (9) 在计算因子得分系数矩阵β时会有负数,但在地下水实际评价中不可能产生负值的影响,因此,在计算时取因子得分的绝对值,可得各指标的权重,其计算结果见图1。 (10) 1.2.3 综合权重 采用因子分析法求的权重ai对相应的层次分析法所得的初始权重gi进行适当的修正,可得到第j个指标的综合权重ωi: (11) 综合权重计算结果见图1。采用层次分析法和因子分析法计算得到的综合权重很好的考虑了客观因素和主观因素对水质评价的贡献程度,是一种相对合理的水质指标赋权方法。 图1 赵川岔地评价指标权重计算 研究区位于河北省西北部,张家口东南部的赵川盆地,地理位置见图2。研究区属于寒温带大陆性季风气候,夏季炎热短暂,冬季寒冷漫长,干燥少雨,多风沙;多年平均气温7.6 ℃,冬季最低气温为-25.4 ℃,夏季最高气温39.1 ℃;多年平均降水量为394.7 mm,降水多集中在七八月,且多为短时暴雨,占全年降水量的50%左右;地下水类型主要由第四系全新统-上更新统冲积含水层潜水、第四系全新统-上更新统坡洪积含水层潜水和蓟县系白云岩裂隙岩溶水含水层潜水;主要的补给来源为大气降水补给,基岩山区侧向径流补给,地表水入渗补给及灌溉回归。 图2 研究区地理位置 表5 研究区域地下水单因子及综合标识指数评价结果 通过计算可知,大部分监测点的单因子水质评价值能满足Ⅲ类水要求,适合人类饮用。少数检测点的个别指标评价结果不能满足要求,Q02、Q04、Q10、Q17和Y01共5个监测点有2个超标指标。 图3 氟化物空间分布及综合水质分布图 本文采用了APH-因子分析来确定综合标识指数法的权重,为了检验这种方法的适用性与准确性,将评价结果与传统的水质评价方法、内梅罗指数法和灰色聚类法的评价结果进行比较,计算结果见表6。结果显示, 4种方法的评价结果几乎是Ⅰ、Ⅱ和Ⅲ类水,其评价结果相近,说明使用其方法对地下水质量进行评价具有一定的适用性。 表6 评价方法结果比较 综合标识指数法与传统的综合水质评价结果一致性很高,达到了94%,但是传统的综合水质评价结果虽与实际结果相近,但其不能对水质的综合类别进行定性的描述;与内梅罗指数法的相似度达64.7%,内梅罗指数法采用的是等权重,其忽略了研究区的各因子之间的差异性对研究区综合水质的影响,也未侧重考虑到指标对身体的危害性;灰色聚类的水质评价结果实际有一定的差异性,其方法对各污染物的危害性反映在变化幅度不同的分级标准中,其忽略了超标污染物对水质的损害,评价结果容易偏轻,从表6中的Q03、Q09、Q11、Q12、Q20、Q21和Q22可以看出,同时其计算过程相当复杂,存在明显的缺陷。由此可知,综合标识指数法更优。 (2)为了避免层次分析法中的主观性对水质评价结果的影响,采用客观的因子分析法与主观的层次分析法对数据进行加权,具有主客观相结合的优点。既考虑了研究区的实际情况,又充分体现了不同的指标在地下水水质评价中的差异性和整体性,使得其结果更加更合理、准确的。 (3)通过对赵川盆地地下水的水质进行评价,并采用传统的水质评价方法、内梅罗指数法和灰色聚类法的评价结果与本文研究方法对比,验证了综合标识指数法的可行性和优势。综合水质标识指数法能直观的判断水质类别及对水质的综合类别进行定性描述是否符合当地要求的质量标准,计算过程简单。
2 实例应用

2.1 评价结果及分析
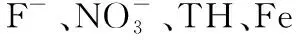
2.2 各方法的评价结果对比
3 结 语


