高中数学化归思想及其应用研究

（吉林省松原市实验高级中学 吉林 138000）

引言

1.化归思想简介

数学思想方法是科学思想、科学方法的一个重要组成部分。化归思维，是一种重要的数学思想方法，化归思想即把未知问题转化为已知问题、把陌生问题转化为熟悉问题、把繁杂问题转化为简单问题，化归思想是解决数学问题的常用方法之一[1]。在数学解题中转化思维的运用极其重要，数学的问题总离不开转化， 化归思想在早期解决数学问题中就有很广泛的应用，如纳皮尔的对数法、笛卡尔的万能方法、著名的哥尼斯堡七桥问题等等[2]。化归的实质就是以运动变化发展的观点，以及事物之间相互联系，互相制约的观点看待问题，善于对所要解决的问题进行变换转化，使问题得以解决。我将高中数学问题所应用到的化归方法进行归纳总结，以便大家可以更直观更具体的解决数学问题，这是我所要研究的重点。本文通过对化归思想的研究和总结，使大家更好的掌握这种解题方法。

一、化归方法与代数

化归思想的实质是揭示联系、实现转化。以下将从二个方面来展示在代数问题中所应用的转化思想。

1.数及代数式的运算

范例1.40颗棋子放在6×8=48个方格中（每格只能放一个棋子），要求各行各列的棋子数均为偶数。试问这样的放法是否可能？[3]

解析：由于每行每列方格数均为偶数，则问题等价于使每行每列空格数均为偶数是否可能，这显然可以办到。如令左上角2×4=8个方格空着即可。

范例2.两人轮流在一张圆桌上摆放大小相同的硬币，每次只能摆放一个，不能重叠，在桌上放下最后一枚硬币者为游戏的胜利者。试问是先放者取胜，还是后放者取胜？[4]

解析：我们先考虑极端情况。假设硬币恰与圆桌一样大小，则先摆必胜。这是因为只要把硬币摆在桌子中心即可。从极端情形中我们可以获得启示；摆的人可以把第一枚硬币占据桌子中心，由于桌面为中心对称，以后不论对方把硬币放至何处，先摆的人总可以把硬币摆在与其成中心对称的位置，故必先摆者取胜。

该例题直接考虑显得比较困难，但是通过把问题极端化，通过对极端位置或状态下问题特性的考察，从而把问题化为比较容易的解决方法，从中引出一般位置或状态下的性质，从而获得解决问题的思路。

2.方程、函数、不等式

法国著名数学家笛卡儿在研究思维原则时曾提出过一个期望，即所谓的能用以解决各种问题的“万能方法”：

第一，把一切问题化归为数学问题；

第二，把一切数学问题化归为代数问题；

第三，把一切代数问题化归为方程式的求解[5]。

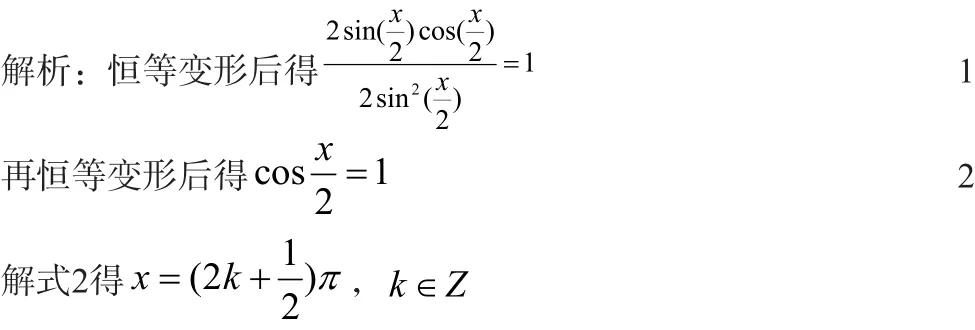
由于与方程式、1式、2式的定义域相同（均为不等于2kπ的所有实数），故此化归为等价化归，即是方程的解。

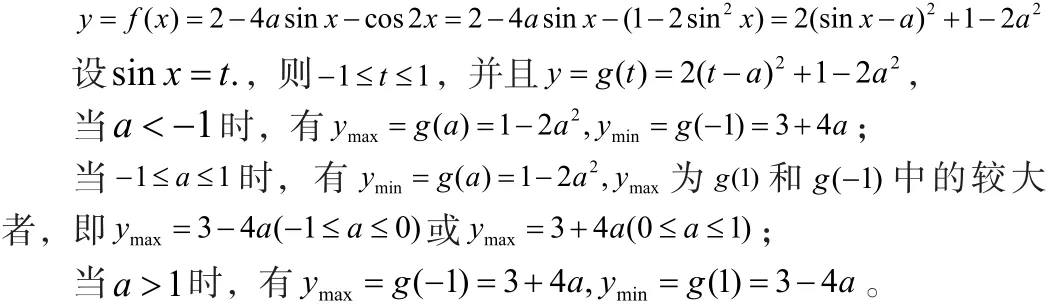
二、化归方法与几何

化归由繁到简目标原则是指化归应朝着目标简单化的方向进行，即复杂的待解决的应向简单的较易解决的问题化归。这里的简单不仅是指问题结构形式上的简单，而且还指问题处理方式、方法上的简单。

1.化归方法与解析几何

解析：如所知，求圆内接三角形面积之最大值是很容易解决的。对于本例而言，我们就可运用压缩变换的方法把椭圆转化为圆。用过圆内接三角形面积的最大值去研究椭圆内接三角形面积的最大值，

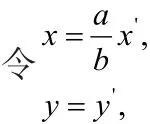
（正三角形），由于在压缩过程中椭圆各点的纵坐标没有变化，因而其内接三角形面积的之高不会变动，只有三角形之底边长变短了，如此，椭圆内接三角形面积的最大值是。

结语

博利亚曾经强调指出：“中学数学教学的首要任务就是加强解题训练”。然而，他所大力提倡的“解题”完全不同于“题海战术”。他主张，与其穷于应付繁琐的教学内容和过量的题目，还不如选择一道有意义但又不太复杂的题目，去帮助学生深入挖掘题目的各个侧面，使学生通过这道题目，就如同通过一道大门而进入崭新的天地。他认为解题应作为培养学生的数学才能和教会他们思考的一种手段和途径，由此可见，加强解题教学，不是搞题型训练，更不是搞题海战术。他的准确含义是通过解题和反思活动，在解题基础上总结和归纳解题的方法，并提炼上升到思想的高度。同时，通过解题活动，充分发挥数学思想方法对发现解题途径的定向、联想和转化功能，突出数学思想方法对解题的指导作用。

通过解题研究，我们可以充分意识到化归思维在解题中的意义。在解题过程中，我们总是将问题由未知向已知转化、由难到易、由繁到简转化，使问题转化为我们已经解决了或者容易解决的问题。