程序配电器减振器结构动力学性能分析

吴泊成 王 镇 姜 晖

（北京航天光华电子技术有限公司，北京 100039）

程序配电器作为箭载控制系统电子设备的重要结构，其工况大多为各种恶劣的振动环境，对安全性和可靠性的要求较高。为保障其在强振动环境下正常工作，通常采用减振器装置降低其振动，并通过振动试验验证其动力学特性。在地面振动试验和研究中，程序配电器及减振器的结构动力学特性仍不明确，还需要分析总结系统动力学响应与激励的关系；需要开展程序配电器振动试验，分析减振器的动力学性能，研究其结构的应力强度及薄弱环节，以确保程序配电器减振器的正常服役。

因此，本文从有限元仿真分析角度出发，进行程序配电器减振器的相关动力学特性及动强度的研究，并且以程序配电器为对象，使用ANSYS Workbench仿真软件对其进行有限元建模和结构动力学分析。所开展的振动试验的动力学仿真分析过程是：预应力下的模态分析→谐响应分析→谱分析（PSD分析）；仿真分析的激励完全按照真实产品试验条件给定。之后，在仿真计算结果的基础上，最终获得了程序配电器及减振器结构在振动试验下的动力学性能和应力强度分布。

程序配电器及减振器的有限元动力学仿真分析，有助于提前寻找出产品设计中的重要缺陷，选择、优化结构设计方案，提高产品可靠性，并由此缩短产品开发时间，降低样机制造及试验成本，为今后程序配电器的研发、设计、生产等工作提供理论性指导。

1 动力学振动试验和分析

对程序配电器及其减振器进行工作环境的模拟振动试验，振动条件分别为5～100Hz的低频段正弦扫描试验和20～2000Hz的高频段随机振动试验，具体试验条件如表1、表2所示，试验外激励频谱曲线如图1所示。

表1 低频段正弦扫描振动试验条件

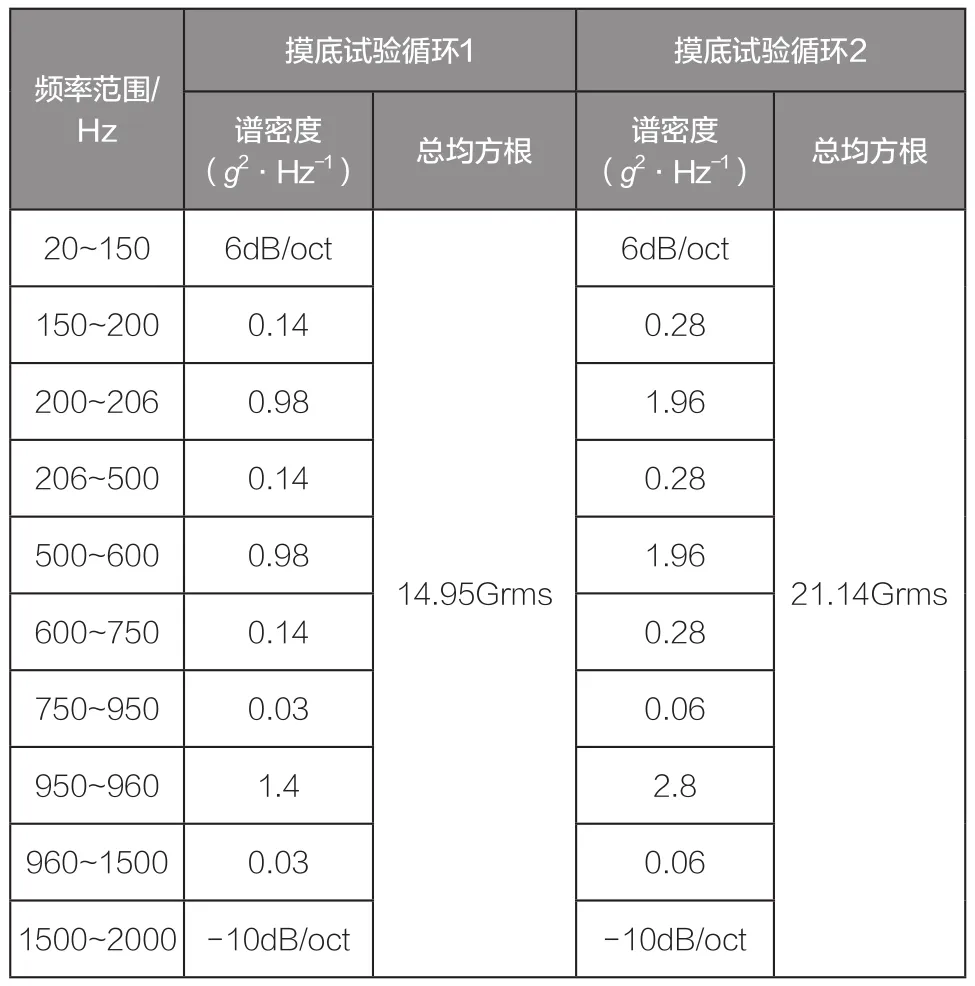
表2 高频段随机振动试验条件

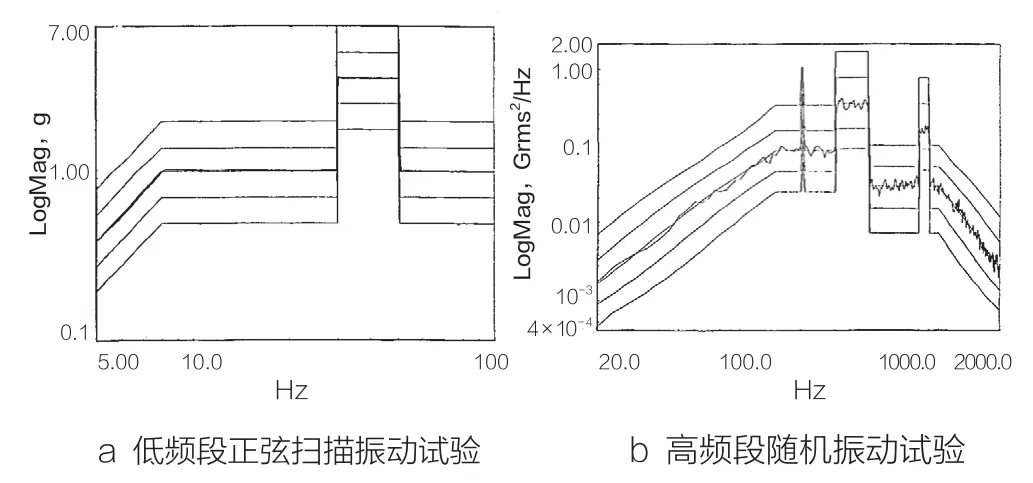
图1 振动试验外激励的频谱曲线图

扫描率：摸底试验循环1R=4.0 oct/min，摸底试验循环2R=2.0 oct/min；振动方向：试件的3个垂直方向。

试验时按试件3个垂直方向，试验时间：每个方向2min。

在程序配电器产品上选取4个测点，测试振动试验中的动力学响应。4个测点位置和振动试验的3个垂直方向见图2。减振器装置在大部分振动工况下能够起到减小振动响应、提高安全性和可靠性的作用，但是在某些特殊振动工况下，会发生失效情况。因此，有必要为程序配电器建立准确的有限元模型，研究产品的动力学特性和减振器结构应力强度，为程序配电器的减振器结构设计提供理论支撑。

图2 程序配电器的4个测点位置和垂直方向示意图

2 程序配电器有限元建模

针对程序配电器结构动力学的有限元分析，首先利用成熟的三维造型软件并根据程序配电器的工程图进行三维几何建模；之后，在ANSYS Workbench软件平台中根据项目情况，分别建立预应力模态分析模块、谐响应分析模块和随机振动分析模块。

本文的模型全部使用ANSYS软件中的Solid185/186实体单元，在软件自适应的网格划分方法的基础上，对不同零部件等结构采用人为控制网格划分方法。从经过软件网格划分后的显示情况可以看出，模型网格划分良好，单元质量度量系数为0.79。对于分析的关键环节，如减振器和机壳等零部件模型，网格划分均匀、细密，以保证后续得到更精确的结构动力学响应结果；对于分析的相对次要环节，如试验振动台平板模型，网格划分规整、粗糙，在不影响计算结果的前提下优化了计算效率，图3为整体和局部模型的网格划分情况。

图3 整体和局部模型的网格划分情况

3 振动试验力学环境仿真

3.1 预应力模态分析

建立有限元模型之后，首先进行螺栓预应力的模态分析。经计算本结构存在减振器螺钉的预紧力为15000N。由于自然状态下振动台静止不动，所以在模型振动台底面施加固定约束。之后，开始进行静力学分析，从而得到结构上的螺栓、螺钉预应力。模型所施加的基本载荷示意图（螺栓、螺钉预紧力和底面固定约束）如图4所示。

图4 模型基本载荷示意图（螺栓、螺钉预紧力和底面固定约束）

带有预应力的模态分析是进行后续分析的基础，在得到各阶模态频率和振型之后，分别开展结构的谐响应分析和随机振动分析。由于后续的谐响应分析的频率范围为5～100Hz，随机振动分析的频率范围为20～2000Hz，为了确保计算的准确性，该模态分析设定的最大频率为1.5×2000=3000Hz，即5～3000Hz，并计算前20阶模态的振动频率和振型。经模态分析得到程序配电器整体结构的前六阶固有振动频率和振型描述，如表3所示。

表3 程序配电器整体结构模态分析的固有振动频率

从模态分析结果和试验实际情况考虑，第一阶模态固有的频率对结构的振动响应影响最大，而且振型为沿X轴水平晃动，直接影响减振器装置的动力学特性。

3.2 谐响应分析

谐响应分析用于模拟程序配电器的正弦振动扫频试验，试验参数见表1，分别对应不同频率范围输入相应的外载激励，从而将试验循环1、试验循环2的外载荷激励分别从X、Y、Z三个方向加载到模型上，并进行程序配电器整体结构的谐响应分析。

由图5中的响应曲线可知，在频率范围为5～8Hz，位移幅值分别固定为4.38mm、8.76mm的外激励下，整体结构的X方向应力最大值针对同一位移幅值激励，其随频率的增长而增大；在频率范围为8～30Hz、加速度幅值分别固定为1.12(g)、2.24(g)的外激励下，整体结构的X方向应力最大值基本均呈恒定状态，未出现任何峰值响应；在频率范围为30～50Hz，加速度幅值分别固定为4.2(g)、8.4(g)的外激励下，整体结构的X方向应力最大值针对同一加速度幅值激励，其随频率的增长而增大；经模态分析可知，整体结构的第一阶固有频率为69.35Hz，所以在频率范围为50～100Hz，加速度幅值分别固定为1.12(g)、2.24(g)的外激励下，整体结构的X方向应力最大值针对同一加速度幅值激励，在固有频率69.35Hz处达到峰值。另外，通过对比试验循环1、试验循环2两条不同曲线可知，整体结构的X方向应力最大值针对同一振动频率，其随量级的增长而增大。

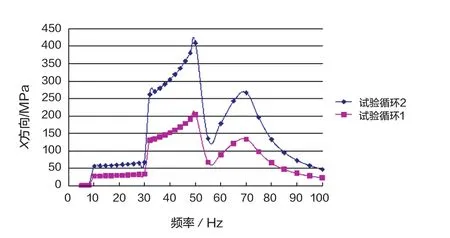
图5 整体结构在X方向载荷下的频率-应力响应曲线图

同理，从图6、图7的曲线可以看出，在固定的外激励载荷下，整体结构的Y、Z方向的应力最大值均未发生明显变化，如在 5～8Hz、8～30Hz、30～50Hz、50～100Hz频率范围内，Y、Z方向应力最大值基本均呈恒定状态，未出现任何峰值响应。分析原因可知，在所涉及的频率范围内，仅包含结构的第一阶固有频率69.35Hz，而第一阶固有频率下的阵型仅为X方向的变形，所以Y、Z方向在第一阶固有频率处不产生峰值响应。同理，对比试验循环1、试验循环2两条不同曲线可知，整体结构的Y、Z方向应力最大值针对同一振动频率范围，其随量级的增长而增大。所以，程序配电器整体结构在Y、Z方向上的动力学响应主要受到来自外激励量级方面的影响。

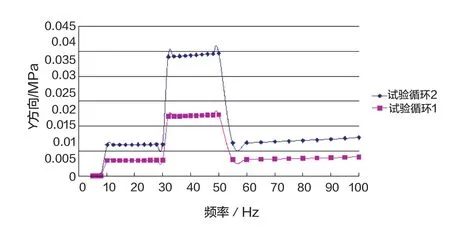
图6 整体结构在Y方向载荷下的频率-应力响应曲线图

图7 整体结构在Z方向载荷下的频率-应力响应曲线图

因此，程序配电器整体结构的X、Y、Z 这3个方向的应力响应，在相同振动频率下均随量级的增长而增大。而在相同的振动外激励量级下，X方向应力响应随正弦振动频率的增长而增大，在结构的固有频率69.35Hz处达到峰值，通过固有频率后结构的应力响应随之减小；Y、Z两方向应力响应，均不受结构第一阶固有频率69.35Hz的影响，没有产生响应峰值。

3.3 随机振动分析

随机振动分析应加载表2的功率谱密度载荷，并分别从X、Y、Z这 3个方向进行3次该激励载荷的加载。通过随机振动分析结果可以得到程序配电器针对不同频率范围和不同激励谱密度量级的动力学响应，进而可以获得减振器动力学性能与外激励频率、量级之间相互影响的规律。

3.3.1 程序配电器随机振动的动力学应力响应分析

对于随机振动分析的动力学响应结果，针对程序配电器的整体结构可以获得等效应力的分布云图。如图8所示，1σ水平的概率分布，即68.269%的时间范围内，整体结构最大等效应力在272.5MPa以下。

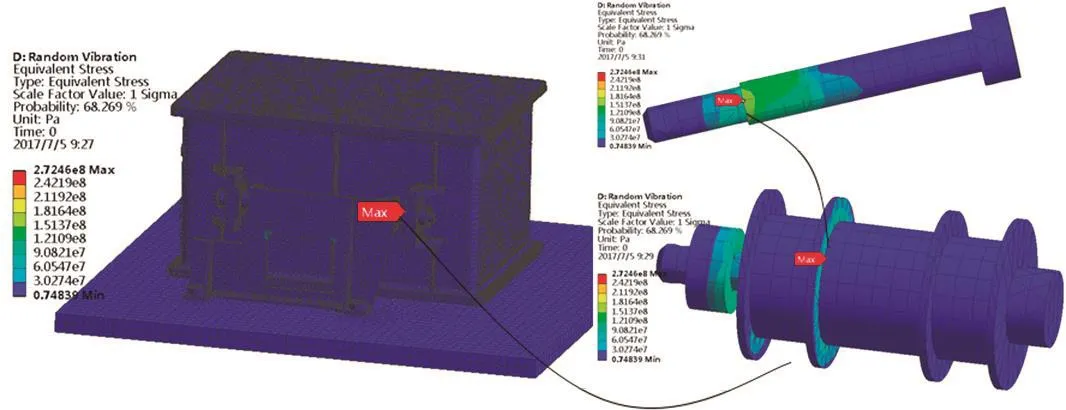
图8 整体结构等效应力1σ水平概率分布云图

3.3.2 减振器螺钉测点4处的随机振动响应分析

同时，通过随机振动分析等效应力概率分布云图可以得到，在随机振动试验时，程序配电器整体结构的等效应力最大值点出现在减振器安装螺钉处。故在随机振动下，减振器装置同样为整体结构的薄弱环节。此时，在减振器螺钉测点4处可以获得该薄弱环节处的频率—加速度的响应谱密度曲线图形，如图9～图11所示。

从图9可以看出，试验循环1、试验循环2在相同随机振动频率范围内，外激励的量级成倍数关系，即试验循环2的激励量级是试验循环1的2倍；试验循环2对应的加速度谱密度响应也大约是试验循环1的2倍。所以可知，在相同的随机振动频率下，程序配电器的动力学响应随着外激励量级的增长而增大。

图9 减振器螺钉探测点处试验循环1、试验循环2激励下的响应谱密度曲线图

另外从图10中可知，在20～150Hz范围下，加速度谱密度响应在69.35Hz附近出现峰值；对应结构的固有频率可知，该响应峰值出现在结构的第一阶固有频率69.35Hz处。从图11中可知，在150～500Hz范围内，由于外激励在200～206Hz频率处出现了一个载荷量级的激增，故加速度谱密度响应曲线出现尖峰。

图10 测点4处在20～150Hz激励下的响应谱密度曲线图

图11 测点4处在150～500Hz激励下的响应谱密度曲线图

3.4 程序配电器减振器动力学特性总结

综上所述，程序配电器及其减振器在低频率正弦扫描振动试验中，对于相同量级（位移或加速度）、不同的频率范围，其应力动力学响应在结构的第一阶固有频率69.35Hz处达到峰值;对于相同频率范围、不同的量级（位移或加速度），其应力等动力学响应随外激励量级的增长而增大。

在高频段随机振动试验中，对于相同量级（位移或加速度）、不同的频率范围，其加速度谱密度响应在结构的第一阶固有频率69.35Hz处出现峰值。对于相同频率范围、不同的量级（位移或加速度），其加速度谱密度响应随外激励量级的增大而增大。

同时，通过实际的振动试验结果和计算机有限元仿真分析可知，程序配电器的薄弱环节在于减振器。尤其在振动试验中，减振器安装螺钉处易发生断裂失效；同时，有限元分析的结果也显示，程序配电器结构的最大应力点均出现在减振器安装螺钉处。所以，减振器安装螺钉的断裂失效等问题需要重点研究和关注。

4 结束语

对程序配电器分别进行谐响应和随机振动的有限元动力学仿真，基本获得了其在低频段正弦扫描振动和高频段随机振动两种振动试验下的动力学特性，基本掌握了程序配电器减振器整体结构的应力分布及薄弱环节，结论总结如下：

（1）获得了程序配电器及其减振器的动力学性能，即在外激励频率方面，主要受结构的固有频率影响较大，在固有频率69.35Hz处动力学响应出现峰值，即产生共振。所以在实际工况下，应避免程序配电器结构的固有频率，或改变相应结构，使其固有频率改变，以达到不影响程序配电器安全服役等目的。

（2）在相同振动频率范围下，振动的外激励量级增大，程序配电器的动力学响应也随之增大。本文中，试验循环2相比试验循环1的外激励量级增大100%，则低频段正弦扫描振动的应力响应也随之平均增长100%；高频段随机振动的应力响应随之平均增长30.8%。所以尽管未达到结构的共振频率，程序配电器及减振器仍有可能因为量级较大而产生失效；应改变相应结构，以提高程序配电器及减振器的动力学承载能力。

（3）明确了程序配电器整体结构在振动工况条件下的薄弱环节，即减振器相关零件部位，尤其是减振器螺钉处，需要重点分析改善，其余部位均安全可靠。