不确定因素理论在阿克苏电网规划中的应用

(中国能源建设集团新疆电力设计院有限公司,新疆 乌鲁木齐 830001)

电网规划作为地区电网发展的顶层设计,是对某地区未来电网蓝图的一种合理谋划。科学的电网规划能切实指导电网的发展建设,起到“经济发展、电力先行”的引领作用。

随着电网发展的智能化与复杂化,电力系统中的不确定因素愈发突出,例如电力需求侧管理技术的采用、电动汽车充电站的接入导致负荷预测的不确定性,分布式电源以及大规模间歇式可再生能源接入导致的发电不确定性,电力市场环境下系统潮流的不确定性以及规划目标的不确定性等。相较于电网设备故障等传统的不确定因素,可再生能源发电、电动汽车充放电等新型不确定因素的不确定程度更大、预测难度更高,对于电力系统的影响也更加明显。为了降低不确定因素对电力系统的影响,有必要从电网规划阶段就开始考虑日益显著的不确定性。针对目前电力系统中各种不确定因素,本文采用最为成熟且应用最广泛的概率模型来表征,并将不确定因素理论应用于阿克苏电网规划。

1 电网规划的不确定因素及其模型

1.1 电源的不确定模型

1.1.1 风电的不确定模型

目前模拟风速随机分布的模型有瑞利分布、Γ分布、耿贝尔分布、Weibull分布等。其中,Weibull分布被公认为是描述风速分布最好的模型。本文采用风速的双参数Weibull分布模型,其概率密度函数为：

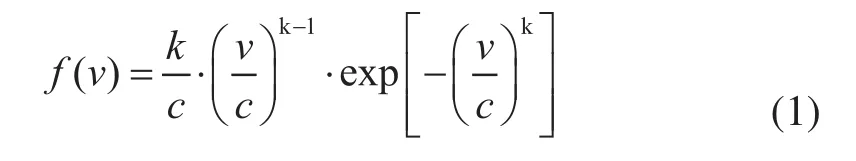
式中：v为风速；k为Weibull分布的形状参数,反映风速分布的特点；c为Weibull分布的尺度参数,反映该地区平均风速的大小。

首先得到风速的随机分布,继而通过风电机组的输出功率与风速之间的关系得到输出功率的随机分布。风电机组有功出力Pw与风速之间的函数表达式如下：

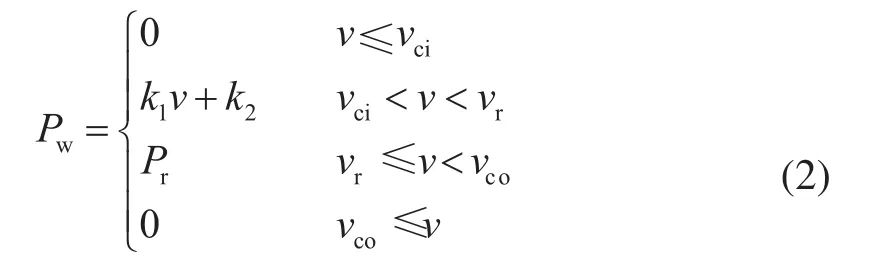
式中：Pr为风电机组额定功率；vci为切入风速；vr为额定风速；vco为切出风速。

风力发电系统通常采用并联补偿器保持功率因数不变,因此,将风电机组简化为PQ节点,无功功率Q为：

式中：P为风电机组有功功率；φ为功率因数角。

1.1.2 光伏的不确定模型

研究表明一定时间内太阳光照强度近似服从Beta分布,其概率密度函数表示如下：

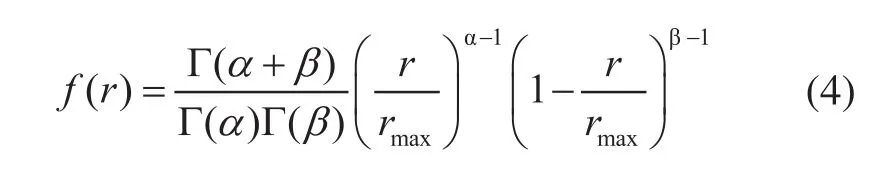
式中：r为某时刻的实际光照强度(W/m2)；rmax为这段时间内的最大光照强度(W/m2)；α和β均为Beta分布的形状参数；Γ为Gamma函数。

然后由光伏发电系统的输出功率与光强的近似关系求出输出功率的随机分布PM：

式中：PM为电池方阵的最大输出功率；A为某一太阳能电池方阵的总面积；η为方阵总转换效率。

通常由并网逆变器自动投切来使光伏发电系统输出功率为单位功率因数,因此,在潮流计算中可将光伏发电系统看作无功出力为零的PQ节点。

1.1.3 常规发电机组的不确定模型

常规火电、水电等发电机组通常处于正常运行状态,当故障或者需要检修时会处于停运状态。因此,本文中的常规发电机组出力的不确定性概率模型设定为服从离散型的二项分布,表示如下：

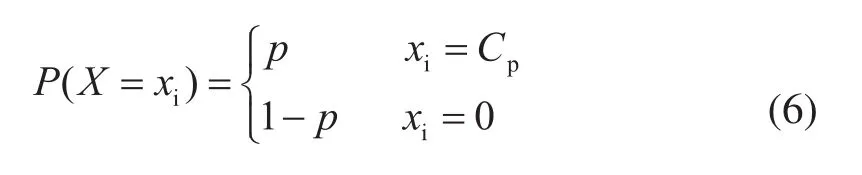
式中：p为发电机组的可用率；Cp为发电机组的额定容量。

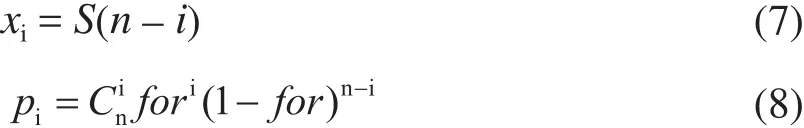
式(7)～(8)中：n为发电机组台数；for为强迫故障停运概率；S为发电机组的单位容量。

1.2 设备故障的不确定模型

表征单一设备故障不确定性的概率模型通常为0－1两状态模型,见公式(9)：

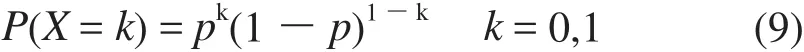
考虑N个设备同时故障不确定性的概率模型服从二项分布：

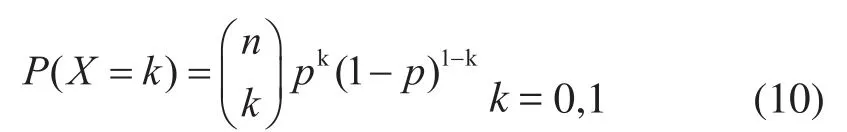
因此,表征设备故障不确定性的数学期望μ=np。

1.3 负荷的不确定模型

随着电力需求侧愈加多样化,负荷的不确定性也大为增加,负荷预测面临更加复杂的情况。目前应用最广泛的考虑不确定性的负荷预测研究结果是近似服从正态分布。对于服从正态分布的负荷,其有功与无功的概率密度函数表达式分别见公式(11)、公式(12)：

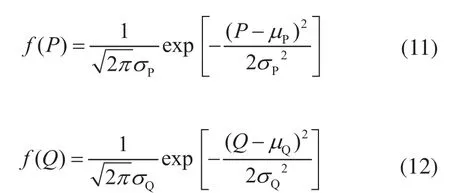
式(11)～(12)中：μ为负荷的数学期望；σ2为负荷的方差。它们可以由文献[6]所介绍的符合正态分布的负荷预测算法求出。

2 阿克苏地区电网存在的问题

2.1 电源存在的问题

阿克苏地区的电源规模远大于用电负荷,电源分布在空间上不均衡,新能源装机规模大幅增加,新能源出力较强的随机性和较弱的可控性,使得电网面临巨大的调峰压力,大量弃水、弃光、火电机组按最低技术出力运行的问题将长期存在。

2.2 网络结构存在的问题

2.2.1 220 kV电网存在问题

阿克苏地区220 kV电网存在的主要问题包括以下三个方面。

(1)220 kV网架结构薄弱。220 kV电网围绕库车750 kV变、阿克苏750 kV变初步形成辐射和链式网架,但目前仍是以110 kV、35 kV电压等级为主体的输、配电网络。

(2)220 kV变电站布点不足,导致局部电网供电可靠性低,运行风险大,经济性差。

(3)220 kV变电站之间负荷转带及互供能力不足。

2.2.2 110 kV电网存在问题

阿克苏地区110 kV电网存在的主要问题包括以下三个方面。

(1)网架较薄弱,电网供电可靠性低,运行风险大。

(2)仍存在一定比例的单线单变、小截面线路、小容量主变和供电半径过长的问题。

(3)110 kV变电站布点不足,配网网架结构优化困难,造成部分电站负荷较重,主变负载率较高。

3 考虑不确定因素的阿克苏电网规划

3.1 电网规划中不确定因素的数学模型处理

针对地区电网中风电出力、光伏发电出力的不确定性,常规发电机组故障停运出力的不确定性以及负荷功率波动的不确定性等,本文采用基于线性化的潮流方程计算模型,并将各节点视为相互独立的随机变量。系统的潮流方程可表示为：

式中：W为各节点有功、无功注入量；X为各节点电压幅值和相角等状态变量；Z为各支路潮流。

考虑到节点注入功率波动的随机性,将式(13)在基准运行点处线性化可得：

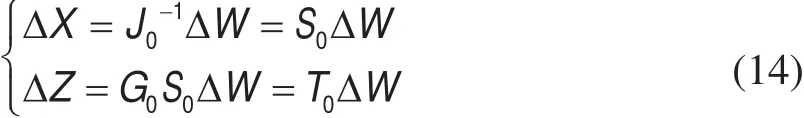
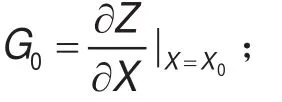
式(14)的状态变量可通过卷积运算求得,为减少计算量,本文采用半不变量法和Gram－Charlier展开级数相结合算法来取代卷积计算。

3.2 不确定因素模型的相关概率理论和算法

针对电力系统中的不确定因素模型,目前主要采用基于半不变量的随机潮流算法。半不变量法具有重要的可加性,能够避免复杂的卷积运算。随机变量的各阶半不变量与其原点距满足以下关系：

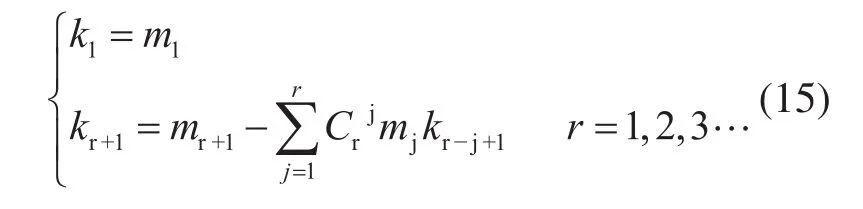
式中：kr、mr分别为随机变量的半不变量和原点矩；r为阶数。

因此,只要根据随机变量的原点矩就能求出其各阶半不变量,反之亦然。

Gram－Charlier级数展开式把随机变量的分布函数表达为由正态随机变量各阶导数组成的级数,而级数系数则由该随机变量的各阶半不变量组成。

根据Gram－Charlier级数展开理论,随机变量的概率密度函数f(x)和累积分布函数F(x)可分别表示如下：

式中：表示规格化后的随机变量μ和σ分别为随机分布的期望与标准差；分别为服从标准正态分布随机变量的概率密度函数和概率分布函数；gv为v阶规格化后的半不变量。

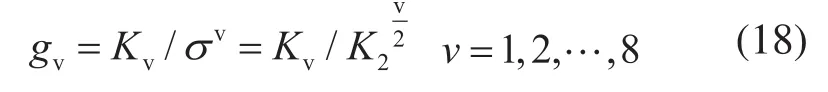
式中的Hγ(x)表示Hermite多项式,它是对φ(x)求γ阶导后的系数,满足以下递推关系：

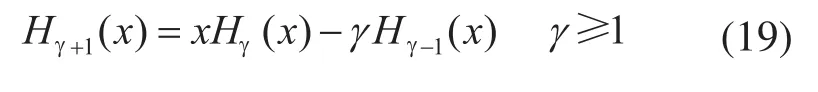
3.3 阿克苏地区电网规划流程及思路

首先在充分了解阿克苏地区电网现状的基础上收集相关资料,综合运用人均电量法、电力弹性系数法、回归分析法、项目法等进行负荷预测；然后对地区电源投产计划进行分析,针对电网存在的问题,综合考虑电力系统“源－网－荷”等不确定因素；在此基础上进行电力电量平衡、变电容量平衡、调峰容量平衡等计算,确定电网电力盈亏情况、规划期需要新增的变电容量及其分布,从而对电网结构进行优化设计,确定电网建设项目与时序；最后对规划方案进行技术校核评估。考虑不确定因素的阿克苏地区电网规划基本流程见图1。

针对阿克苏地区柯坪县、乌什县、阿瓦提县等光伏基地光伏出力波动较大的特点,根据本文提出的概率潮流算法,求出其出力期望及系统中各节点电压与支路潮流的概率分布及越限概率,从而选择对应的变电容量规模及导线型号,配置合理的无功补偿装置,保证新能源出力对主电网的影响最小。针对电网中网架薄弱环节,分析其N－1甚至N－2通过率,通过科学合理增加变电站布点,优化梳理网架结构,满足网络结构的不确定对电网的影响。同时,加强对电力负荷的预测,综合考虑电采暖、电动汽车充电设施等“电能替代”负荷的不确定性,为电力调度部门提供合理的参考价值。

3.4 阿克苏地区电网规划方法

本文结合阿克苏地区电网实际,分别从电源、网架、负荷三个方面阐述考虑不确定因素的规划方法在阿克苏地区电网规划中的应用。

(1)电源方面

阿克苏地区新能源以光伏为主,以阿瓦提光伏基地为例,规划至“十三五”末光伏装机达300 MW。考虑其光伏出力特性,结合本文提出的不确定性理论,进行系统方案的对比分析见表1。

通过考虑光伏实际平均出力水平,可以有效减少工程建设规模,减少投资,同时分析得出节点电压越限概率,为控制系统电压提供有价值的参考。

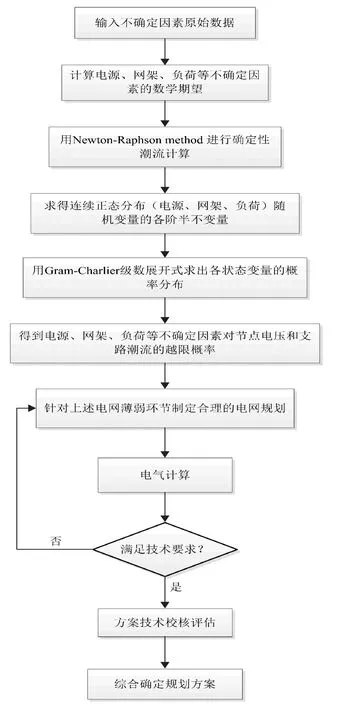
图1 考虑不确定因素的电网规划基本流程

(2)网架方面

以阿克苏地区220 kV主网架为基础,分析220 kV电网重要节点电压及支路潮流越限概率,找出电网薄弱环节,从而提出可行的解决方案。

以温宿变与阿克苏市电网补强方案为例,考虑温宿区域小水电装机较多,夏季水电大发期间通过温宿变上网电力,使得节点电压偏高,线路潮流较重,一旦现有温宿变至白水变I回线路故障,将造成温宿区域解网,为此需考虑网架补强。

方案一：补强温宿－白水Ⅱ回线；方案二：新建温宿－棉城I回线。运用基于半不变量法和Gram－Charlier展开级数的不确定理论计算分析两种规划方案：方案二即本文考虑网架不确定性的规划方案,节点电压与支路潮流越限概率均较低,不仅能够形成环网加强网架结构,提高供电可靠性,而且较方案一中温宿－白水线路发生N－2概率更低,解决断面受限问题,提高清洁能源送出能力,实现电力在更大范围内优化配置。两个方案对比详见表2。

(3)负荷方面

考虑电采暖、电动汽车等不确定性负荷影响,分析其负荷特性,运用概率理论求得负荷期望值。假设至“十三五”末阿克苏市新增电采暖、电动汽车等夜间负荷与电能替代等白天负荷报装容量各150 MW,常规方案考虑新建1座主变为2h180 MVA的220 kV变电站。本文从负荷特性综合分析,几种不确定负荷同时率较低,实际最大负荷将维持在150 MW左右,实际上一期工程只需新建1台主变。系统方案对比见表3。

表1 规划电源系统方案对比

表2 规划网架系统方案对比

表3 规划负荷系统方案对比

(4)综合分析

综合考虑各种不确定性负荷特性,运用概率理论预测负荷期望,本文规划方法能够提供切实可靠的规划方案,实现协调发展,避免不必要的投资。

综合分析电力系统中“源－网－荷”等不确定因素,考虑电源、负荷的不确定性评估将有效降低工程建设规模,减少不必要的工程投资；考虑网架结构的不确定性评估方案较常规规划方案供电可靠性更高,有效解决断面受阻问题,提高清洁能源送出能力。综合考虑“源－网－荷”等不确定因素的电网规划,不仅能够减少不必要的投资,而且有效降低系统节点电压以及支路潮流越限概率,构筑坚强网架结构,提高供电可靠性。

通过考虑阿克苏地区电网中的各种不确定因素,科学合理规划地区网架结构,至2020年阿克苏电网将形成坚强智能的220 kV电网,满足阿克苏东西部电网解列运行,分区供电,逐步形成结构简明、清晰合理的220 kV网架结构。同时进一步强化周边110 kV电网的建设,优化梳理110 kV网架结构,使阿克苏地区电网成为网架健全、经济合理、安全可靠、运行灵活的和谐、统一电网。

4 电网规划方案校核

4.1 电网潮流及调相调压计算

综合考虑电力系统“源－网－荷”等不确定因素,运用概率理论,求得各不确定因素的数学期望。由于主电网的系统电抗X远大于系统电阻R,不同于低压配电系统间的阻抗关系,考虑采用牛顿－拉夫逊法进行潮流计算。通过对阿克苏地区电网规划水平年正常解环运行方式下的潮流计算,系统各线路均未出现过载现象,系统各点电压均在合理范围之内,电网的输送能力显著提高,电源送出压力得到缓解,潮流分布更加合理,输、配电能力得到显著加强。

4.2 电网静态安全稳定分析

应用N－1准则校验本电网内各单一元件无故障断开或单一元件故障断开后的电力系统安全稳定问题,结果表明,系统各节点电压合理,线路无过载现象,电网结构强度和运行方式满足安全运行要求。

4.3 电网暂态稳定分析

本文采用瞬时三相短路扰动估算电网承受短路故障冲击的能力,同时还包括计算重要线路发生三相短路故障不重合和重要线路发生单相短路故障重合成功的情况。故障地点选择在对稳定影响最不利的母线和线路出口处。本次计算稳定判别条件为发电机功角差不超过150°,1 s内电压波动不低于额定值的0.75 p.u.,1 s内发电机频率不低于49.5 Hz。通过对规划水平年网架的暂稳计算,系统稳定水平较好,可以满足安全稳定需要。

4.4 电网短路电流水平校核

水平年内规划项目全部实施后,网架结构联系更加紧密,通过短路电流校验,发现对系统的短路电流影响不大,系统短路电流水平较好,并且对电气设备选择无特殊要求。

5 结语

本文在考虑了当今电力系统中“源－网－荷”等不确定因素的基础上对阿克苏地区电网规划进行了分析评价,综合考虑各种不确定因素对电网规划带来的影响,对阿克苏地区主电网进行统筹规划,合理布局,解决电网薄弱环节,校验考虑电力系统中不确定因素的电网规划的科学合理性。结果表明,不确定因素理论能够客观全面地反映当今电力系统普遍存在的不确定性问题,有效指导地区电网规划。