中子时空动力学内瞬态热工反馈计算的分析

明平洲,李治刚,潘俊杰,安 萍,芦 韡,刘 东,余红星,孙玉发

(1.中国核动力研究设计院核反应堆系统设计技术重点实验室,四川 成都 610213;2.中国核动力研究设计院,四川 成都 610213)

事故分析以及瞬态工况分析是反应堆堆芯计算的重要组成部分。随着计算机软硬件的演变,多学科代码的耦合能够更真实地模拟反应堆行为。中子物理和热工水力是广为研究的耦合计算方案,在堆芯尺度内,它能够对堆芯复杂的瞬态工况进行细致描述,为设计或系统安全分析提供多种参数。中子时空动力学在扩散计算近似条件下可以提供堆芯内部瞬态过程中重要中子学参数随时间的变化,通过耦合热工反馈计算功能,提升计算准确度,且瞬态工况下在数值求解时包含时间变量的离散和空间变量的离散。论文基于核动力院现有的研究条件和计算方案[1],提取和集成自研软件CORTH[2]内的瞬态热工反馈计算功能,为完整的堆芯耦合计算方案提供原型参考。除开对瞬态热工反馈计算功能的解读,福清机组的插棒提棒问题也将用于实际堆芯问题的数值验证。

1 计算方案简介

中子时空动力学模型如式 (1)所示。式中,下标g代表能群,能群数为G;下标i代表缓发先驱核组,组数为ND。ϕg(→r,t)为g群中子通量密度;ci(→r,t)为第i组先驱核浓度;vg为g群中子速度;Dg为g群扩散系数;Σr,g和Σf,g分别为g群移出截面和裂变截面,Σs,g′→g为g′群到g群的散射截面;ν为每次裂变释放的中子数;χg为瞬发中子裂变谱;χg,i为缓发中子谱份额;λi为先驱核衰变常数;βi为缓发中子份额。

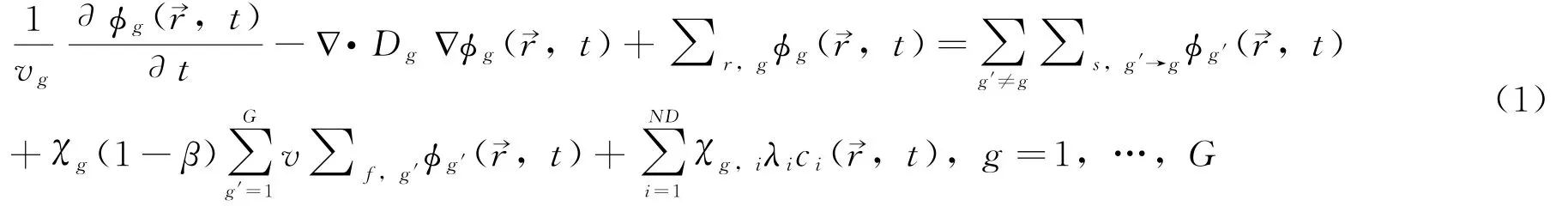
整个中子时空动力学计算方案现阶段以瞬态中子学计算为主干,获得堆芯的三维功率分布信息。热工反馈计算根据相应信息计算得到堆芯内部的温场分布,从而引起堆芯各个位置处的截面数据变化,再影响瞬态中子学计算的结果。由于这些非线性关系,总的数值方法采用源迭代方法来消除非线性关系,获得各个瞬态时刻的堆芯内参数分布。相应计算方案如图1所示。

图1 计算方案的流程图Fig.1 Flow chart of the calculation scheme

时间离散方面,龙格库塔方法是精度较高的常微分方程数值解法。相关研究在隐式欧拉格式基础上采用精度从1阶到4阶的对角线隐式龙格-库塔方法 (DIRK),并利用Richardson外推和嵌入低阶方法实现了时间步长的自适应,该方法具有良好的稳定性和较高精度[3]。根据式 (1),相应的数学模型可以简化为式 (2)。式 (3)则是利用式 (2)推导得到的一阶龙格库塔数值形式,即向后欧拉格式。实际计算方案可以采用更精确的二阶DIRK方法进行时间离散。每一级的求解与向后欧拉格式时间离散后的求解形式是相似的,区别只在于替换每一级的时步和初值。

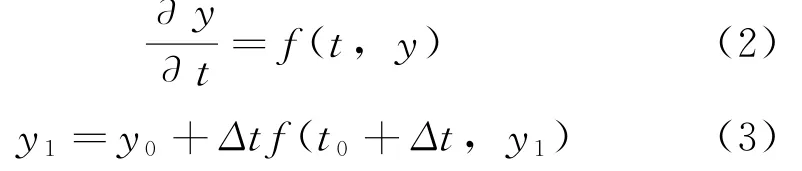
中子学计算方面主要分为扩散计算和截面更新计算两部分。其中扩散计算在时空动力学中主要指代瞬态扩散计算,它可以通过固定源问题下的格林函数粗网节块法进行求解[3]。截面计算则采用读表插值的方法,利用组件程序提供的截面库,根据各个瞬态时刻的状态参数来更新堆芯内部的截面数据。现阶段计算方案中根据计算问题的性质和侧重点,选定冷却剂密度和燃料有效温度两个状态参数。瞬态计算在进入之前通过稳态计算或读取状态数据库来提供初始时刻的通量、先驱核的分布,对应的热工反馈计算从图1可以明确,位于每个瞬态时刻的扩散计算与截面更新计算之间,该内容将在论文中进行详细解读和分析。

2 热工反馈计算的分析

2.1 概述

热工反馈计算主要根据三维全堆芯的功率分布或通量分布,计算得到堆芯内部的温场分布。与中子学部分耦合之后,相应的热工参数将作为状态点,用于截面计算,反过来影响堆芯的功率分布。通过多次数值迭代计算达到平衡。这里热工反馈计算从CORTH程序中进行提取,这里将对相应的计算进行解读和分析。

2.2 热工反馈计算

考虑到工程计算的易用性,选择单通道模型来进行热工反馈计算,此时热工反馈计算部分的轴向分段应与中子学部分保持一致,但仅仅考虑活性区;径向上也与中子学的粗网格保持相同大小,例如中子学瞬态扩散计算按照组件进行粗网格的划分。由于按照组件进行了通道划分,因此整个热工反馈计算由两层循环进行数值计算,如图2所示。

图2 热工反馈计算的伪码描述Fig.2 Pseudo code description for the thermal feedback calculation

这里遍历各个组件进行热工参数计算,从计算机编程角度进行解释:首先根据中子学代码提供的功率信息对每个组件的各个轴向分段求解表面平均热流密度dens,然后调用Cal FuelSig函数求解各个网格处 (由组件与轴向分段进行划分)冷却剂的密度和燃料有效温度。由于区分了热工反馈计算过程内的数值变量和中子学单学科代码所依赖的数值变量,所以最后在反馈计算完成之后需要进行耦合数据的赋值操作。

2.3 冷却剂密度和燃料有效温度的计算

瞬态单通道模型不考虑横向流动,因此按照燃料组件遍历时各个通道内的质量流速和压降比较明确,不需要求解动量守恒方程便可完成热工反馈所需参数的计算。瞬态单通道模型从燃料元件中心开始将通道在径向上分为6个控制体,所以某个通道的各个分段冷却剂温度信息需要保存6个,与商业软件PRINA类似。其中,燃料芯块划分为4个控制体,包壳和外部慢化剂分别作为1个控制体。

图3中燃料棒径向分为6个控制体,其中1,2,3为燃料芯块,4为燃料芯块和气隙 (如果存在),5为包壳,6为冷却剂。按照各个控制体生成三对角矩阵,求解得到冷却剂温度等信息。此时瞬态单通道模型中采用的假设为:不考虑轴向导热,不考虑流体势能,动能为常数且均匀,且流体流速方向在同一高度共线。因此瞬态单通道模型中只需要求解能量守恒方程便可完成反馈计算。

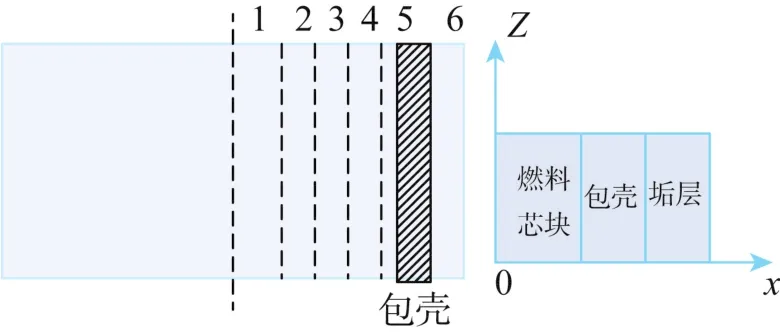
图3 燃料元件的控制体划分Fig.3 Mesh partition of fuel element

芯块控制体:

气隙控制体:

包壳控制体:

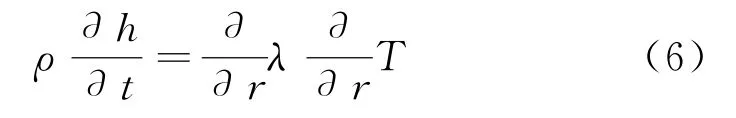
慢化剂控制体:

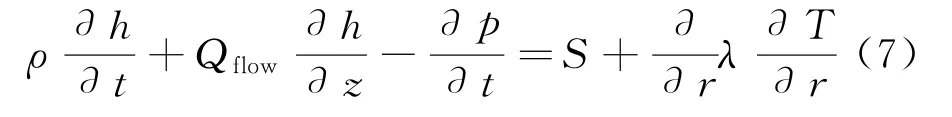
以上能量守恒方程中S为内热源,离散化之后可得到相应的三对角形式方程:

相关系数A、B、C、α均使用已知量计算,涉及到控制体相关的几何参数、热物性和换热系数等内容。对于棒状燃料元件,瞬态当前时刻的冷却剂温度为前一时刻与当前时刻冷却剂温度的平均值。冷却剂密度可以通过物性函数的转换,将冷却剂温度转化为密度信息。

瞬态情况下需要考虑上一时刻的燃料温度信息来计算导热系数以及当前时刻燃料有效温度的初始状态。计算燃料芯块温度常常包含有芯块外表面温度、中心温度以及有效温度等内容,同时求解燃料芯块温度时需要区分板状燃料元件 (军用)和棒状燃料元件,然后按照轴向分段对各个分段进行遍历求解。计算方案中集中在棒状燃料元件的求解,在径向上将燃料元件进行分区,如图2所示分为三个分区,整个芯块温度的计算便围绕这些分区展开,径向上利用一维热传导方程进行求解。

最终燃料芯块的中心温度计算得到后,利用加权方法,联合燃料芯块的外表面温度获得燃料芯块的有效温度值,计算公式为:

3 数值实验

使用福清5&6号机组第1循环寿期初的瞬态例题对整个计算方案进行数值验证。该例题为热态零功率的初始工况 (零功率条件下热工反馈较小,但可以观察数值稳定性和敏感性等内容),其中N1棒组以1.2步每秒的速度插入,183.3 s时再以1.2步每秒的速度提出,366.6 s离开真实堆芯的活性区,统计堆芯500 s的瞬变过程。实验中真实堆芯的轴向分为20段,并利用商业SMART软件进行对比验算。

固定步长运行方式主要指代龙格库塔时间离散的计算步长取为固定,实验中取为0.1 s;而自适应步长运行方式表明采用嵌入低阶格式以估计当前时步的计算误差,在计算过程中可能放大或缩小计算步长,减少计算次数。整个计算过程中输出模拟瞬态时间500 s内的相对功率变化趋势,反映该物理问题的瞬变过程。

分析一:由于相对功率值偏小,纵坐标的数值取对数,便于对比数值的变化趋势。从图4中可以看到,在瞬态时间200多秒时SMART计算结果出现了相对功率先降低后升高的波谷情况,子通道模型下固定步长或自适应步长的计算结果与SMART参考解的趋势一致,相对功率均经历了先降后升的过程。利用数据处理工具比较单通道模型下固定步长与自适应步长的相对功率值差异,两者的相对偏差最大为0.98%,说明两者吻合较好;比较单通道模型下固定步长与SMART计算结果的差异,相对功率值的相对偏差最大为17.5%,最小为10.3%,即计算结果存在一定偏差。值得注意的是相对功率的波谷处SMART计算结果与论文内子通道模型的计算结果偏差约为1%左右,说明瞬态模拟的关键事件位置不存在较大误差,这里考虑计算结果在其他瞬态时刻的偏差可能来源于商业软件SMART内置的部分参数与数值实验中使用的控制参数不一致导致。

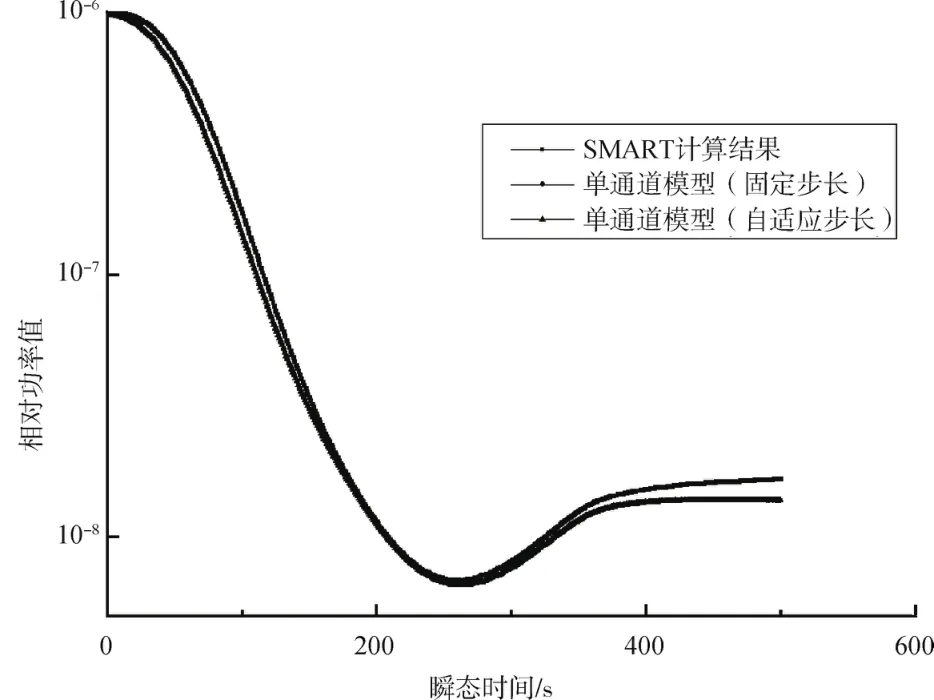
图4 瞬态过程的相对功率变化图Fig.4 Relative power trend of transient process

分析二:统计在工作站服务器HP Z800a上的计算时间,固定步长的计算时间为5 353.78 s,自适应步长完成计算则耗时为314.38 s。实验中记录得到固定步长情况下热工反馈计算次数为50 000,自适应步长情况下热工反馈计算次数为236。这表明自适应步长在本例题中能够较多减少离散计算的时间点个数,所以串行情况下本瞬态例题自适应步长的计算效率优于固定步长的计算效率,且正确性上两者几乎保持一致。

分析三:瞬态时间250 s左右相对功率值达到波谷,但实际上控制棒组在180 s左右插入到堆芯底部再提出。统计瞬态时间范围内热工参数的数值大小,整个瞬态时间区间内冷却剂密度的变化和燃料有效温度的数值变化在本例题中并不明显,但变化趋势与插棒提棒动作比较吻合。这里以轴向第十层的组件为例,其坐标为 (6,6)和 (8,8),(8,8)位置对应堆芯径向正中心组件。绘制对应节块在计算过程中冷却剂密度和燃料有效温度的变化趋势图,图5表明冷却剂密度变化比燃料有效温度更为剧烈,180 s左右降到最低,且径向上控制棒组附近的热工参数变化幅度比堆芯正中心组件更大;从参数敏感性上来看,燃料有效温度受控制棒组在轴向上的移动较小,其中一段瞬态时间的数值未明显变化,符合本例题代表的物理问题特点。

综上所述,本文阐述的计算方案具备在中子时空动力学计算过程中提供瞬态热工反馈计算功能,且通过真实堆芯例题可以初步归纳,现阶段在计算结果上符合该例题对应真实瞬态过程的变化趋势。尽管热工参数的影响遵循堆芯内部的物理过程,但计算精度上与SMART商业软件存在着少量偏差,这些偏差可能来源于多个因素,并不影响原型方案的有效性。

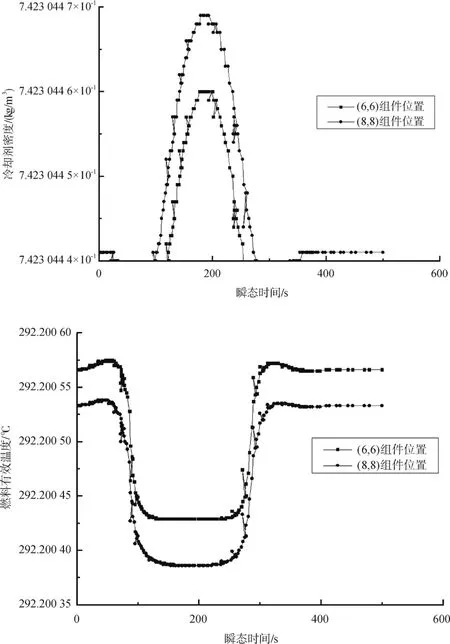
图5 热工反馈参数的变化图Fig.5 The variation of thermal feedback parameters

4 结论

本文在中子时空动力学的计算过程中引入了瞬态热工反馈计算功能,通过对热工反馈计算内容的解读和分析,说明了整个计算方案在堆芯问题域内的求解流程,为中国核动力研究设计院相关专业软件的研制提供原型参考。与此同时,真实堆芯的数值实验初步论证了整个原型计算方案的正确性和有效性。随着研究的进一步深入和拓展,子通道模型以及CFD方法将对热工反馈计算进行替换和对比验证,同时先进的并行计算等内容也将引入到计算方案中进行计算效率的增强。