CO2中激波脱体距离的弹道靶实验测量和数值计算
廖东骏, 柳 森, 黄 洁, 简和祥, 谢爱民, 王宗浩
(中国空气动力研究与发展中心, 四川 绵阳 621000)
0 引 言
21世纪以来,火星探测活动的日益频繁,需要大量的气动数据为火星探测器设计提供依据和验证。目前,火星探测器高超声速气动特性研究主要采用地面实验和数值模拟相结合的方式,地面实验的主要目的之一是为数值计算方法提供可靠验证数据。 激波脱体距离是验证数值模拟准确性的常用依据之一。圆球或球头模型是研究激波脱体距离的标准模型之一,无法正确预测圆球激波脱体距离意味着无法正确预测飞行器的激波形状和压力分布,从而影响飞行物体总体气动特性的预测[3]。国内外开展过大量激波脱体距离测量实验,但主要在空气条件下进行[4-6]。而火星大气由95.3%的CO2、2.7%的N2、1.6%的Ar和其他微量气体组成[7],与地球大气成分存在显著差异。进行CO2条件下的激波脱体距离测量实验对相关数值计算方法的验证有重要意义。
高焓脉冲设备如激波风洞等常用于开展激波脱体距离的测量实验。MacLean等[8]和Doraiswamy等[9]在反射式激波风洞中测量了CO2条件下,速度V=1.91~3.37km/s、压力p=1.01~1.62kPa的火星科学实验室缩比模型头部的激波脱体距离,采用2种模型计算了激波脱体距离,包括基于类似Millikan-White半经验公式得到的修正的松弛时间和双温度模型的CV-pτ模型和将化学-振动耦合分为2步、考虑16组分间每种可能反应的CV-16模型,但数值计算结果显著低于实验数据。MacLean等进一步的研究表明,在膨胀风洞中开展同类实验,数值计算得到的激波脱体距离则可与实验数据较好地吻合[10]。反射式激波风洞自由来流气体的离解程度高于膨胀风洞/管[11],一般数值计算难以描述其自由来流状态,采用反射式激波风洞实验数据验证数值算法将增加计算的复杂性。因此,需要获得自由来流与真实飞行环境更为接近状态下的激波脱体距离实验数据,才可有效验证相关数值计算方法。
弹道靶通过发射器将模型加速到所需速度并在试验段自由飞行,可模拟真实的飞行速度、雷诺数及高焓的飞行环境[12],不存在自由来流化学反应问题[4],是进行CO2条件下激波脱体距离测量的理想设备。
Park的双温度非平衡模型[13]在高超声速非平衡流计算中被广泛采用。对火星大气CO2条件,也有很多研究采用双温度模型计算探测器的气动力热特性[14-16]。但双温度模型是基于空气条件提出,其转动温度等于平动温度的假设在CO2条件下适用性如何,需要获得更多的CO2条件下激波脱体距离实验数据加以验证。
在中国空气动力研究与发展中心超高速所超高速弹道靶上进行了CO2条件下的激波脱体距离测量实验,以积累实验数据,研究验证Park双温度非平衡模型在不同实验状态下的适用性与准确性。实验在纯CO2条件下进行,模型为直径D=10mm的均质圆球和头部半径Rn=12.5mm的火星着陆巡视器缩比模型。实验获取了上述模型的激波脱体距离和激波形状数据并与双温度模型计算结果进行了对比。
1 实验方法与状态设计
1.1 实验设备
实验在中国空气动力研究与发展中心超高速所超高速碰撞靶和气动物理靶[17]上进行,图1给出了弹道靶实验布置示意图。2个靶主要由发射器、测速控制系统、靶室、真空系统、靶室压力/温度测量系统和成像系统等构成。其中,发射器为二级轻气炮,用于发射模型到预定速度;测速控制系统采用激光探测器测量模型飞行速度并为成像系统提供触发信号;靶室由爆震段和试验段组成,分别用于模型/弹托分离和激波脱体距离的测量;真空系统可为实验提供所需的靶室压力;靶室压力/温度测量系统采用电子真空计和温度计测量试验段靶室压力和温度;成像系统采用瞬态激光阴影成像方法拍摄实验流场,所用光源为脉宽10ns的YAG激光,波长为532nm,能量为150mJ,有效测试区域直径为100mm,分辨率为100线对/mm,成像光路布置如图2所示。当模型飞行速度为2~4km/s时,脉宽10ns的光源对应运动模糊量b=0.02~0.04mm,对驻点激波层厚度δ为0.4mm的情况,b/δ=5%~10%。运动模糊量会影响测试精度,造成判读误差,具体的误差分析见1.3节。
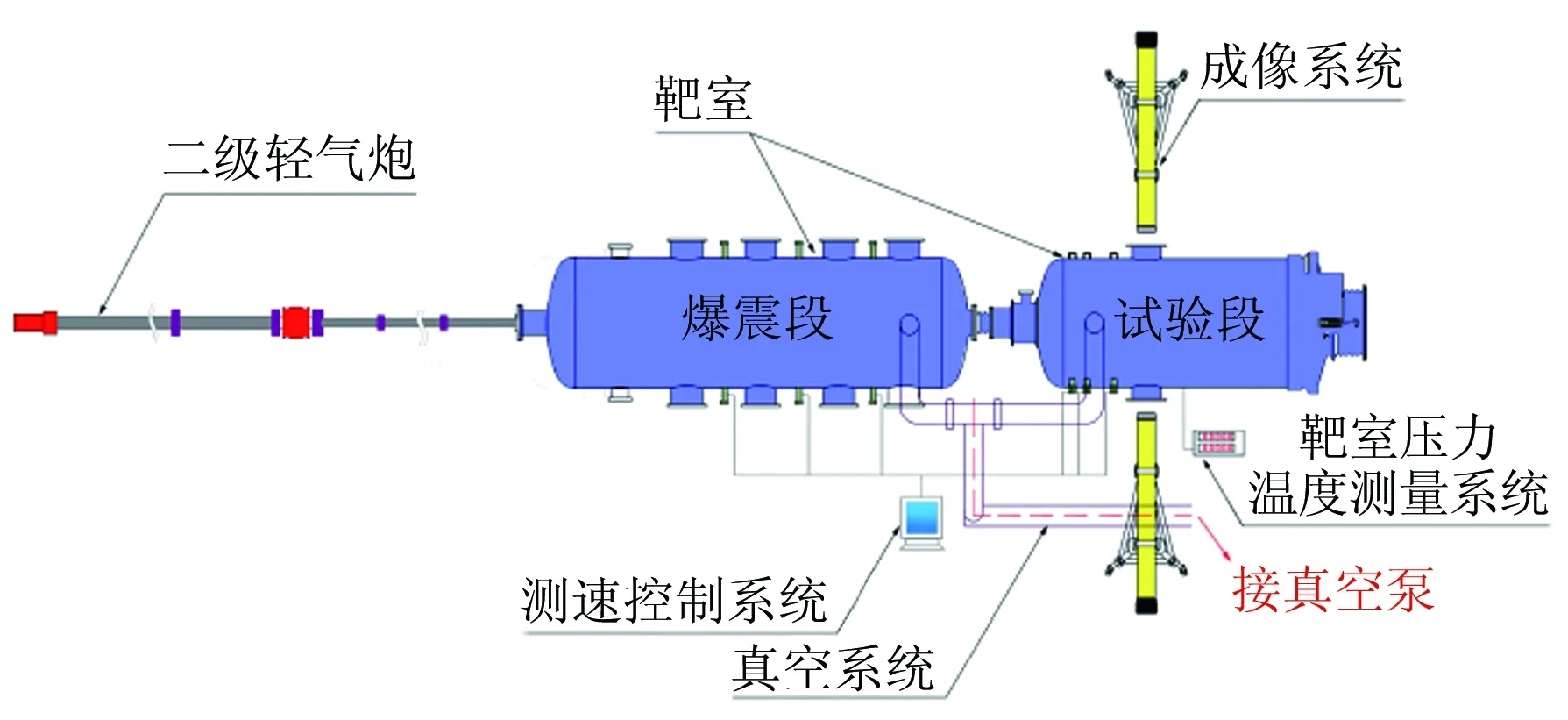
图1 弹道靶实验布置示意图
1.2 实验模型与状态设计
圆球模型为均质Al2O3球,直径为10mm,质量约2.1g,如图3所示。着陆巡视器模型由大底(钢)和尾端(聚碳酸酯)2部分装配而成,大底直径为25mm,头部半径为12.5mm,质量约19.2g,如图4所示。2个模型均由4瓣弹托包裹发射。

图4 着陆巡视器模型与弹托
实验的模型飞行速度主要参考海盗号进入器进入段25~40km高度的速度范围(约2~4km/s)[23],实验靶室压力选取为约2~12kPa。
1.3 数据测量方法
实验基于阴影图像测量模型激波脱体距离。以圆球阴影图像图5为例:沿模型垂直轴线(VL)测出图像上模型直径的像素Px1,沿模型水平轴线(HL)测出图像上模型头部激波层外边缘到模型表面之间距离,即激波脱体距离的像素Px2,则圆球模型头部的激波脱体距离δ与模型直径D存在如下比例关系:
(1)
即圆球模型头部的激波脱体距离δ为:
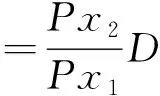
求得δ后,除以对应圆球模型的半径即得到无量纲化的圆球头部激波脱体距离δ/R。着陆巡视器模型的激波脱体距离数据测量方法与圆球类似,主要测量模型头部激波脱体距离δ,并除以模型头部半径Rn得无量纲激波脱体距离δ/Rn。根据误差传递公式,可由(2)式得到激波脱体距离δ的测量误差E:
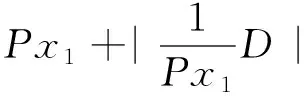
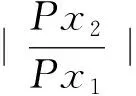
式中ΔD为模型的直径误差;ΔPx1和ΔPx2分别为测量时由于图像质量和运动模糊量等原因引起的模型直径像素和激波脱体距离像素的判读误差。ΔD根据模型实际测量的直径误差确定,ΔPx1和ΔPx2根据对同一图像的多次判读确定。着陆巡视器模型激波脱体距离数据测量与误差计算方法与此类似。
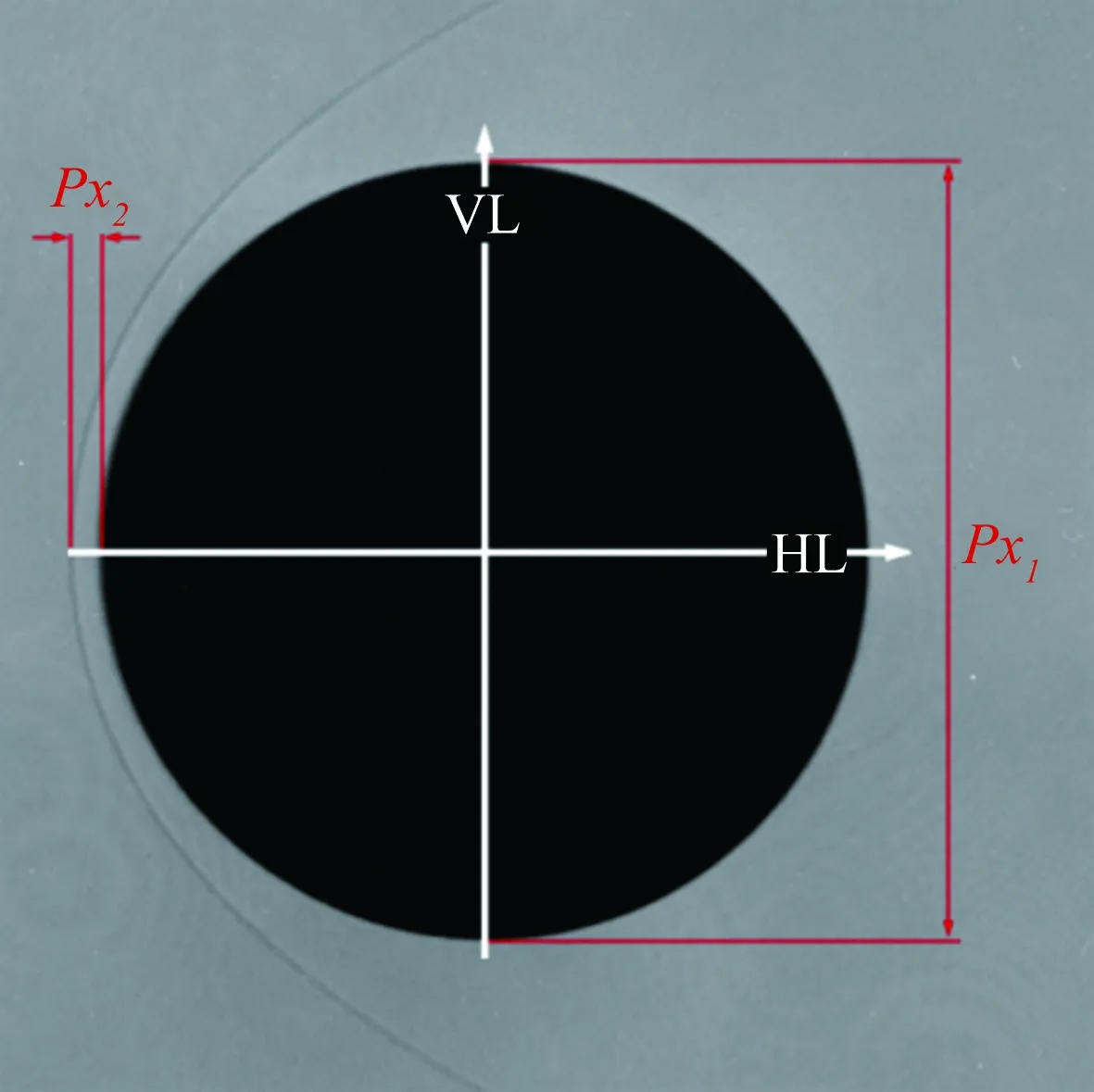
图5 圆球激波脱体距离测量方法示例
Fig.5Schematicofthemeasurementmethodoftheshockstandoffdistance
2 数值方法与模型
2.1 控制方程与状态方程
非平衡流动控制方程采用带化学反应源项的二维轴对称N-S方程组,在计算坐标系(x,r,θ)下,其无量纲形式表达为:
(4)
式中Q为守恒量矢量,F、G为对流项矢量,Fv、Gv为粘性项矢量,H、Hv为有粘、无粘部分源项矢量,W为化学反应和振动源项矢量,Re为雷诺数。对双温度非平衡模型,有:
Q=(ρi,ρu,ρv,ρE,ρev)T(5)
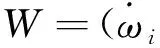

状态方程为:
(7)
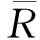
对控制方程(4)对流项采用对称型TVD格式离散,粘性项采用中心差分格式离散,化学反应和振动源项采用一阶精度的隐式处理。
2.2 化学反应动力模型
采用Park的5组分(CO2,CO,O2,O,C)8反应化学反应动力模型[18]描述CO2条件下的非平衡流动,其反应方程为:
其中m1和m2为催化体,分别为m1:O2,CO2,CO;m2:C,O。上述反应具体反应常数见参考文献[18]。
2.3 振动-离解耦合模型
采用Park的耦合模型[19],对于本文涉及的化学反应分别有:
(1) 离解反应如AB+M↔A+B+M,正、反向反应控制温度为:Tf=(TTV)0.5,Tb=T;
(2) 置换反应如AB+C↔A+BC,正、反向反应控制温度为:Tf=Tb=T。
上述T为输运温度,Tv为振动温度。
2.4 计算网格与边界条件
本文计算网格为二维轴对称结构网格,网格数目为100(Inflow)×120(Outflow),并根据实验结果在激波位置处加密,如图6所示。计算时,入流边界条件根据自由来流条件给出,出流边界条件直接由内点外推插值得到,壁面边界为粘性无滑移等温壁,对壁面组分计算采用完全催化壁条件,壁面组分质量分数取来流组分质量分数。
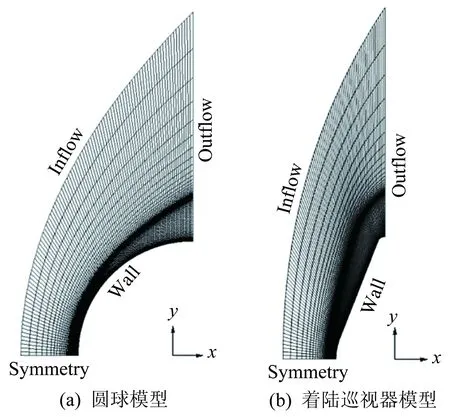
图6 计算网格示意图
3 结果分析与讨论
实验共获得4个有效数据(圆球3个,着陆巡视器1个)。图7和8分别给出了1次圆球(C10-1)和1次着陆巡视器模型(C10-4)实验的阴影图像,可见对本文实验状态,采用阴影成像可以捕捉到清晰的模型脱体激波图像。表1和2分别给出了圆球和着陆巡视器模型头部激波脱体距离测量数据和对应的实验状态。

图7 实验C10-1阴影图像(D=10mm,V=2.122km/s,p=12.300kPa,ρR=1.1×10-3kg/m2)
Fig.7ShadowgraphofthetestC10-1

图8 实验C10-4阴影图像(Rn=12.5mm,V=2.802km/s,p=1.836kPa,ρRn=4.1×10-4kg/m2)
Fig.8ShadowgraphofthetestC10-4
图9给出了根据实验C10-1和C10-4来流状态计算的驻点附近密度分布云图和实验阴影图像的对比。可见计算得到的激波脱体距离与实验图像基本吻合。
图10对比了各次实验模型头部激波脱体距离的实验数据和对应计算结果,同时给出根据冻结模型和双温度非平衡模型计算的ρR=1.0×10-4kg/m2时的圆球激波脱体距离随速度的变化曲线作为参考。表3

表1 模型头部激波脱体距离测量数据和对应实验状态Table 1 Shock standoff distances at the spheres’ nose under various test conditions
* 雷诺数以直径10mm计。

表2 着陆巡视器头部激波脱体距离测量数据和对应实验状态Table 2 Shock standoff distances at the entry vehicle models’ nose under various test conditions
* 雷诺数以大底直径25mm计。

表3 模型头部激波脱体距离实验数据与计算结果对比Table 3 Comparison between tested and the calculated shock standoff distances at the models’ nose

图9 计算密度云图与实验阴影图像对比
Fig.9Comparisonbetweentheshadowgraphandthecalculateddensitycontour
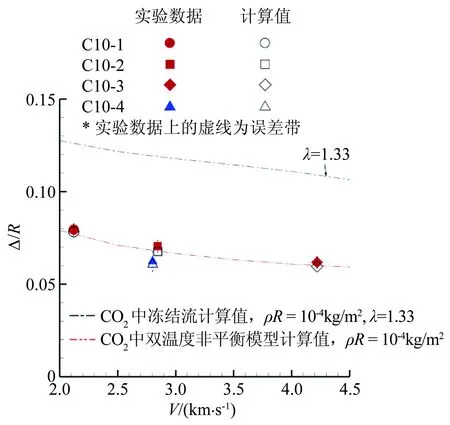
图10 模型头部激波脱体距离实验数据与计算结果的对比
Fig.10Comparisonbetweenthetestedandthecalculatedshockstandoffdistancesatthemodels’nose
给出了详细的实验和计算结果,以及计算结果相对实验数据的偏差。采用双温度非平衡模型计算的结果相对实验数据的偏差均小于对应实验数据的测量误差。由此认为,采用双温度非平衡模型能够较准确地再现本文CO2条件下的模型头部激波脱体距离。图11对比了实验C10-1的脱体激波形状和采用双温度非平衡模型计算得到的结果,可见计算结果与实验数据基本吻合。图12对比了按照实验C10-1状态计算的模型驻点线上的平动温度T和振动温度Tv分布,可见在激波后靠近激波一侧的区域,T与Tv有显著差别,非平衡现象显著。对本文其他实验也存在类似结果,由此推测,本文CO2条件下绕模型的流动主要为非平衡流动。
需要注意的是,本文实验条件下,模型的飞行速度低于5km/s,而现有的火星探测器进入速度最高可达7.6km/s[20]。在更高的流动速度下,双温度非平衡模型是否继续适用,需要更多的实验数据加以验证。
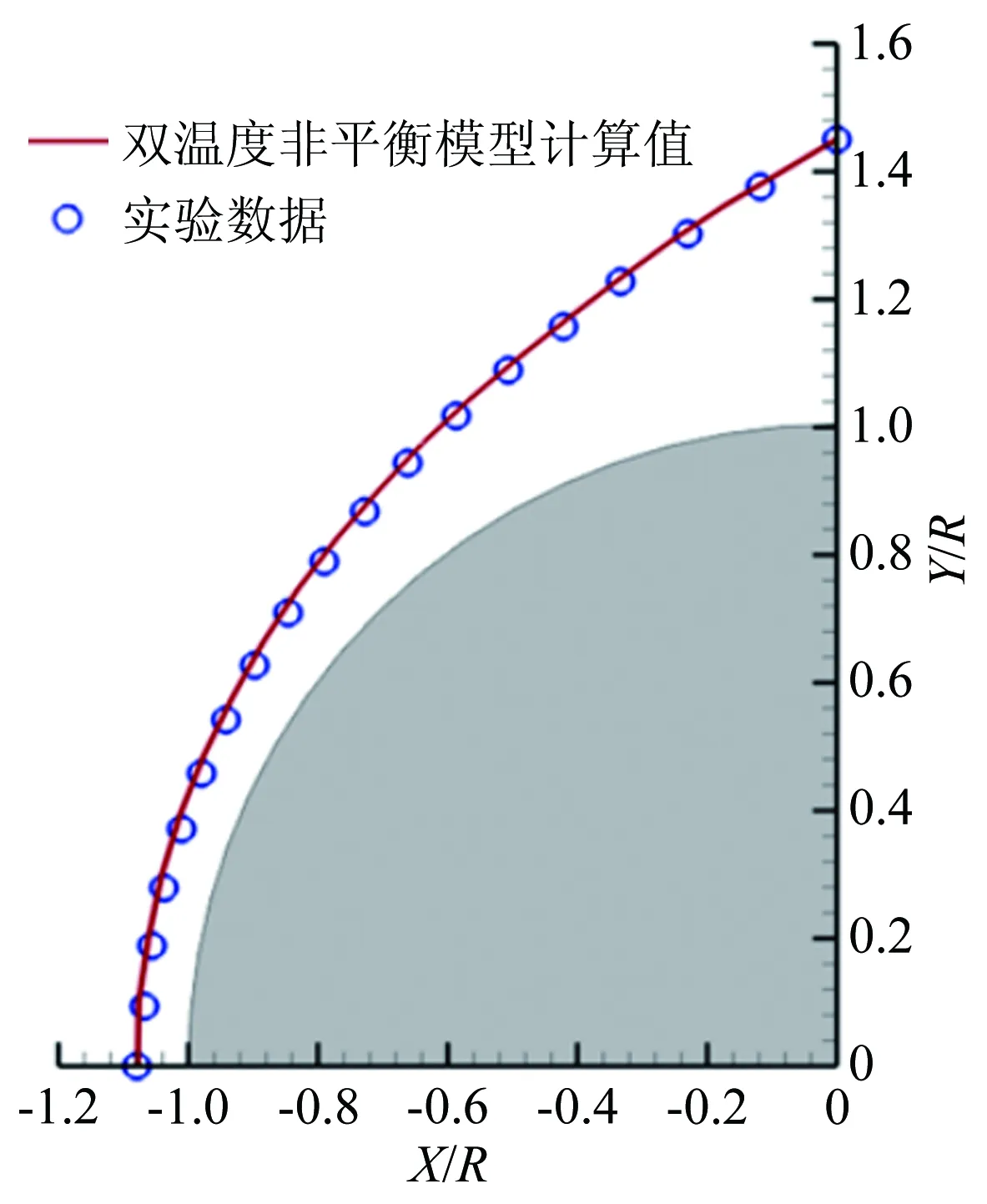
图11 实验C10-1脱体激波形状和对应的计算结果对比
Fig.11ComparisonbetweenthetestedandthecorrespondingcalculatedshockshapeofthetestC10-1
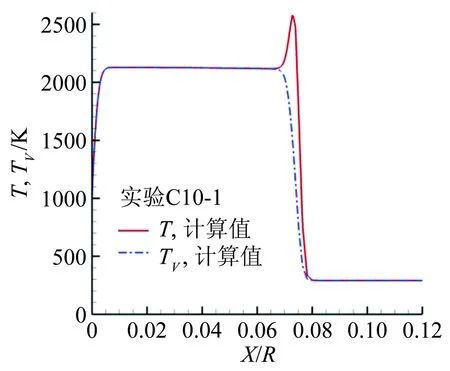
图12 C10-1状态下模型驻点线上平动、振动温度分布计算结果
Fig.12CalculatedtranslationalandvibrationaltemperaturedistributionsalongthestagnationlineofthemodelundertheconditionofC10-1
同时,本文研究的热力学温度模型和化学反应动力模型是比较单一的,在双温度非平衡模型适用性与准确性充分研究的基础上,可进一步开展CO2条件下多温度模型(如同时考虑平动、振动和转动温度)和不同化学反应动力模型对数值计算准确性影响的研究工作。
4 结 论
在中国空气动力研究与发展中心超高速弹道靶上进行了CO2条件下圆球和着陆巡视器模型的激波脱体距离测量实验,获取了CO2条件下靶室压力为2.42~12.30kPa、飞行速度为2.122~4.220km/s的圆球和靶室压力为1.836kPa、飞行速度为2.802km/s的着陆巡视器模型头部激波脱体距离实验数据。实验数据与双温度非平衡模型计算结果进行了对比,得到如下结论:
(1) 采用双温度非平衡模型能够较准确地再现本文CO2条件下模型头部激波脱体距离;
(2) 根据计算结果推测,本文实验状态下绕模型流动主要为非平衡流动;
(3) 需补充更高模型飞行速度(>5km/s)的实验数据,验证CO2中更高流速状态下双温度非平衡模型的适用性与准确性,并进一步研究多温度模型和不同化学反应动力模型对CO2下非平衡流数值计算准确性的影响。

