对应县木塔1962年实测数据的再分析*

张毅捷 叶皓然 韩 效 ZHANG Yijie, YE Haoran, HAN Xiao

0 引 言

应县木塔位于山西省应县县城西北的佛宫寺境内，又名佛宫寺释迦塔。该塔建造于辽清宁二年（1056年）①，总高约67.31 m[1]，是世界上现存最古老，也同时是最高大的木结构古建筑。

前学研究表明，东亚的很多木结构古建筑的实测数据中存在着“模数控制”现象【[1-7]，因此用“模数制”理论分析古建筑实测数据是深入了解东亚古代木结构建筑设计手法的基本方法之一。

近代对应县木塔的调查研究始于1933年，当时由梁刘两位先生带领莫宗江、纪玉堂进行了实测，并于1935年完成了1∶50的实测图（莫图），后因战争原因，这些最初的研究成果保存得并不是很好，1942年又由陈明达在莫图的基础上完成了1∶20的实测图（陈图）。1954年路鉴堂指导井庆升等按照陈图制作了缩尺模型。1962年文物出版社再次组织实测，并于1966年将研究成果出版专著《应县木塔》[8]。这本书既是应县木塔里程碑式的研究成果，同时其中收录的实测图纸（陈图）、实测数据和历史文献的摘要是应县木塔最基础的研究资料，因此这本专著是应县木塔研究重要的基础文献。对应县木塔的建筑设计手法的第二个重要研究出现于20世纪90年代：张十庆[3]，新世纪还有傅熹年[5]和肖旻[6]的研究，2013年张十庆又对此前的研究进行了修正【[7]。这四位先生的研究无一例外都是从分析《应县木塔》中所公布的实测图和实测数据出发，探讨其中的“模数制”问题。通过四位学者的研究，应县木塔的建筑设计手法的基本情况已较为明了，但其中仍有一些不够完善之处，本文将尝试沿着前学的思路继续深入这些问题。

1 应木塔中的模数制

1.1 回顾过往的研究

陈明达早在20世纪60年代初就发现了应县木塔中的“大模数”现象——在应县木塔的高度实测值中频繁出现一个尺度：883 cm，这个数值同时与应县木塔的第三层外檐柱头总开间尺寸一致，结合《营造法原》的相关记载，陈先生认为这个883 cm即为应县木塔设计中的一个较大的模数——这个模数同时与高度和平面尺寸相关（图1）[1]。傅熹年也注意到了相似的规律，并进一步结合日本古代楼阁式木塔的实例，认为这个“大模数”的设计手法体现了楼阁式木塔设计手法由“底层柱高法”向“中间层总面阔法”转变的一个中间过程[5]。

而更为细致的“模数法”则由张十庆首倡于1990年，在其博士论文中不仅从整数尺的角度分析应县木塔的实测数据，他认为陈明达所发现的大模数883 cm即为30辽尺，他的另一个重大的学术贡献在于发现了存在于这些实测数据中次一级的“模数”（基准长）现象，并指出这一模数恰好是前述“大模数”的二十分之一，即1.5辽尺（44.2 cm），同时还指出0.75辽尺（22.1 cm）也可能是模数；之后他又对应县木塔的用材进行分析，发现这一模数与建筑用材之间没有明显直接的关系[3,7]。2002年肖旻在其博士论文中也曾对应县木塔的设计手法进行研究，他认为应县木塔的模数（基准长）并非1.5辽尺（44.2 cm），而应该是0.75辽尺（22.1 cm）[6]。肖旻也没有就这一“模数”与材分制的关系进行深入。

1.2 本文的研究

傅熹年在1992年的研究中发现：日本学者在法隆寺五重塔中找到的模数与该建筑的栱木用材尺度一致，而药师寺东塔、室生寺五重塔中的模数则精细至“分”的尺度②，也就是说此时建筑的模数不是孤立存在的，它除了控制空间尺度之外，还控制着标准构件的尺度。于是这里就产生了一个问题：应县木塔中所发现的模数是否也存在着更为精细的分值？答案是肯定的。

陈先生和傅先生在应县木塔中发现的大模数为883 cm，这个尺度后为张十庆先生证为准30辽尺[3]。张十庆在这个基础上又发现了更次一级的模数：883÷20=44.2 cm=1.5辽尺；而肖旻在此基础上论证“44.2÷2=22.1 cm=0.75辽尺”是更为精确的模数尺度。

根据《应县木塔》可知，该塔的分值为1.7 cm③，22.1÷1.7=13，即肖旻所找到的模数22.1 cm刚好是13“分”，而张十庆找到的模数44.2 cm则为26“分”，约略相当于一材两栔④。

据《应县木塔》，该塔各层材栔大小不一，但是其中用材使用最多的是25.5 cm×17 cm⑤，这个尺度换算成“分”值刚好是15“分”×10“分”，而栔使用最多的是11 cm，差不多是6.5“分”。普拍方的尺度为32 cm×17 cm≈19“分”×10“分”，阑额的尺度为36 cm×17 cm≈21“分”×10“分”。另外，替木厚和驼峰厚亦为17 cm=10“分”。显然从构件用材来看1“分”=1.7 cm是一个更次一级的模数值。

在陈明达20世纪70年代的研究中，曾将应县木塔几个主要的尺度用1“分”=1.7 cm折算，其结果也非常漂亮[8]59-60（表1）。再次证明1“分”=1.7 cm这个最次一级的模数的存在，并且这个最次一级的模数参与控制一些大的空间尺度。

图1 应县木塔高度设计规律（陈明达案）Fig.1 design law of size of height in Pagoda of Yingxian Muta (scheme speculated by Mingda Chen)

表1 应县木塔部分大尺度列表（陈明达案，1“分”=1.7 cm）Tab.1 list of large real measurements in Pagoda of Yingxian Muta (scheme speculated by Mingda Chen, 1 “fen”=1.7 cm)

其中特别值得注意的是，每层外檐间广（柱头尺寸）的递减值为25“分”。《营造法式·看详·取径围》中有八棱的尺度设定方法：“八棱径六十，每面二十有五，其斜六十有五”[9]，也就是说每面缩减25“分”，就可以根据这种“八棱”的计算方式，快捷地确定八棱径和斜长方便施工。这也从另一侧面说明“分”对空间尺度的控制作用。

也就是说，在这座塔中存在着从大到小三级模数：883 cm、22.1 cm、1.7 cm。这样的模数体系也是符合实情的，在决定建筑中比较大的尺度的时候采用883 cm作为大模数，可以很方便地确定建筑大的比例关系；而22.1 cm模数的存在，可以对中等规模的空间尺度进行调整；最后1.7 cm的模数的存在则可以方便地统一处理数量庞大的各种构件尺度之间的协调，也可以辅助空间尺度的微调。

2 应县木塔的分高度设计

2.1 回顾过往的研究

陈明达在分析应县木塔的总高度设计的时候，发现了该建筑的“大模数”=883 cm，并拿这个大模数和实测图相对应，结果发现普拍方的断面高度都应该算在每层普拍方下的柱子的设计高度之内[1]48；之后在建筑的分高度设计分析中，陈先生将每层塔身的高度又分为两段：下层檐柱普拍方上皮至平坐普拍方上皮和平坐普拍方上皮至上层檐柱普拍方上皮，而每层的两个分高度分别对应高度值一致[1]48；在此基础上陈先生发现了高度设计中的一些尺度节奏规律[1]48-49（图1）。从该图可见，应县木塔的高度设计中的确存在着某种尺度规律和节奏，但是这个尺度的规律性还不够漂亮、简洁。

张十庆1990年的研究中也探讨了应县木塔的分高度设计问题，他是将应县木塔的分高度换算成其所推测的辽尺，数据比较简洁，分高度的分界方式同陈明达[3,7]，这从另一个侧面证实了陈明达案的正确性。但是这两个分高度尺度的节奏分别是14.5辽尺（427 cm）和15.5辽尺（457 cm）（图2），和张十庆所发现的基准长1.5辽尺（22.1 cm）之间没有简洁的数学关系。

肖旻在2002年的研究中对普拍方的归属问题提出了质疑，他认为“普拍方和铺作同属横向构件，而柱子为竖向构件，从结构逻辑来说，其分层不太合理”，之后他将各层普拍方计入其上方的分高度中，发现高度构成更合理，唯一的不足是底层檐柱柱高（不含普拍方）的推定吻合性有所降低，误差达到6 cm[6]190-191。

综合上述三位学者的研究可以发现以下两点：第一，应县木塔的高度尺度构成中的确存在着规律和节奏；第二，但是上述三家的规律和节奏分析都不太理想，于是就为本次研究提供了思路和继续深入的空间。

2.2 本次的研究

笔者在对日本古代楼阁式木塔的实测数据进行分析时，提出了“柱间高”的概念[10]。所谓柱间高，就是在中国传统木结构古建筑立面三分的概念（单栋建筑由台基、屋身和屋架构成）的基础上认为，楼阁式木塔是将每层的平坐部、柱额部、斗栱部和屋架部反复重叠而上形成构架主体；由于日本古代的楼阁式木塔的斗栱部和屋架部有很多斜材，不能简单地进行水平分层，而平坐部往往只有柱脚方一个构件；因此最终将日本的楼阁式木塔在高度方向上分为柱高和柱间高两种高度构成（图3）。所谓柱间高就是，下层柱子顶部到紧邻的上层柱子的底部的高度值。根据对日本12世纪末之前的11座楼阁式木塔的实测数据的分析可知，法隆寺五重塔和净琉璃寺三重塔的柱高和柱间高应该都是经过设计的结果⑥。于是就产生了一个疑问：应县木塔的柱间高是否也同样经过了设计？遂分析如表2。

由表2可见：

底层柱高≈A=40N=520a=884 cm（30辽尺）

第一段柱间高≈第二段柱间高≈第三段柱间高≈二层柱高≈三层柱高≈四层柱高≈0.5A=20N=260a=442 cm（15辽尺）

第四段柱间高≈17N=221a=375.7 cm（12.75辽尺）

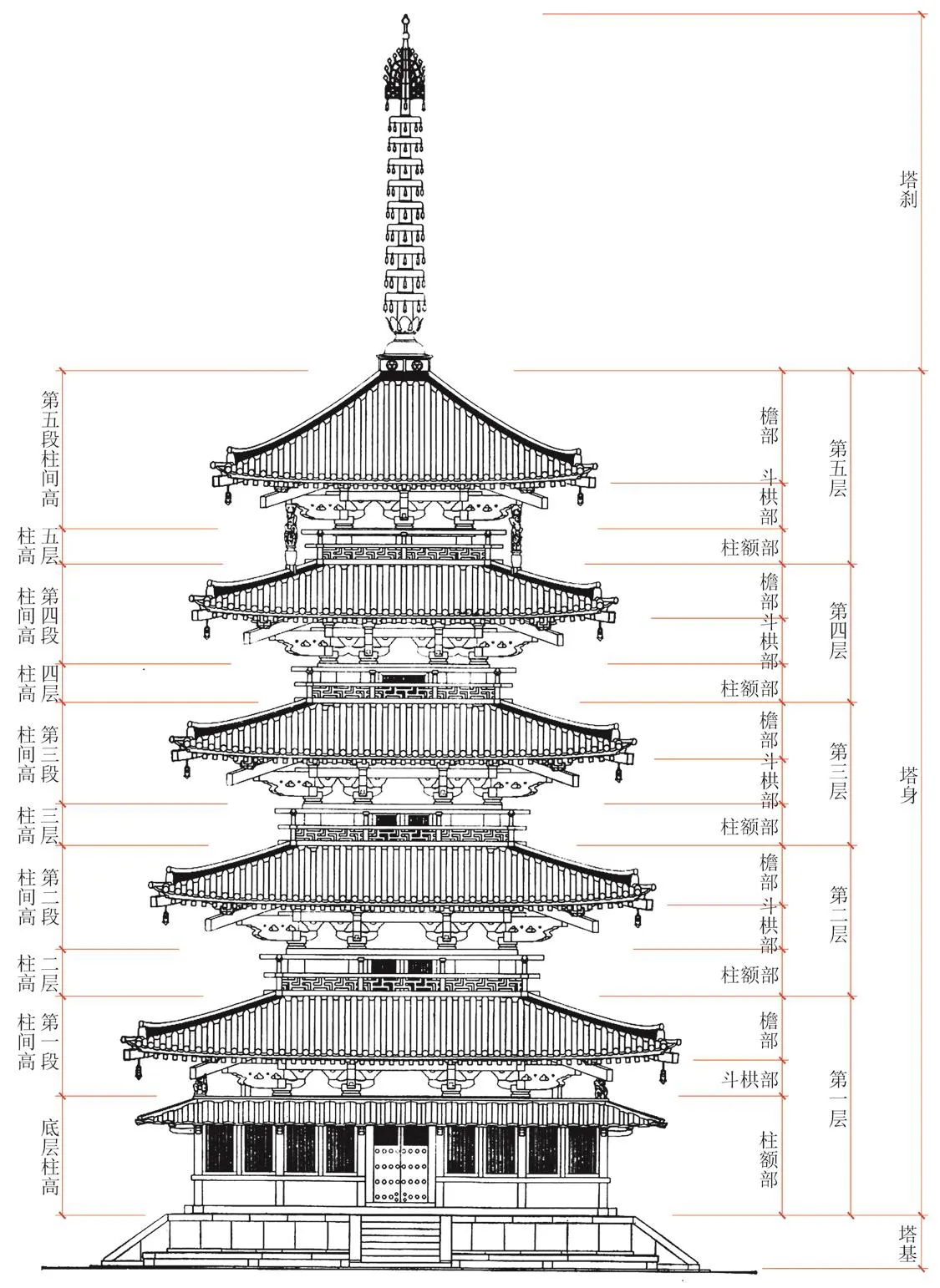
图3 日本古代楼阁式木塔高度构成分析·法隆寺五重塔Fig.3 analysis on composition of height in multi-storied wooden pagoda in Japanese ancient period ( fi ve-storied wooden pagoda in Horyuji Temple)

第五层柱高≈18N=234a=397.8 cm（13.5辽尺）

第五层屋架高≈45N=585a=994.5 cm（33.75辽尺）

这一方面表明前述对本建筑“三级模数制”的分析思路的正确性，同时也表明上述针对普拍方的归属划分是合理的。也就是说不能简单地把普拍方都划归其下方的柱额部，而应该区别平坐部的普拍方和屋身部（柱额部）的普拍方，即除了底层屋身部之外所有的普拍方都应该计在平坐部，而二到五层的屋身部（柱额部）则都不包含普拍方。

表2 应县木塔分高度实测数据分析（“柱高—柱间高”法）Tab.2 analysis on real measurement data of size of height in Pagoda of Yingxian Muta (method of height of column and height between columns in adjacent layer)

3 应县木塔的总高度设计

3.1 回顾过往的研究

陈明达在20世纪60年代初的研究中指出，应县木塔塔身高加塔刹高为第三层外檐总面阔（柱头尺寸）的7倍；塔基高为第三层外檐总面阔（柱头尺寸）的倍，因此塔总高为前述标准尺度的7倍。并且该塔塔总高大致为第三层外檐柱头外接圆直径的3.157倍，而3.157≈π，也就是说塔总高约为第三层外檐外接圆的周长[1]46-49。张十庆在20世纪90年代初的研究中将上述塔身高、塔基高、塔刹高和塔总高都分别折算成辽尺，数据都比较漂亮，显示出整数尺法在该建筑总高度设计中得到应用的可能性[3]89。傅熹年在2001年的研究中发现，应县木塔的总高度不仅是第三层外檐总面阔的整数倍，同时是底层柱高或底层副阶柱高的整数倍，结合其对日本古代楼阁式木塔的研究，这两种模数控制现象（“中间层总面阔法”和“底层柱高法”）也先后出现于日本的古代的楼阁式木塔中，遂指出“大约中国盛唐以前之塔以一层柱高为模数，中国中唐以后，塔高兼以中间之面阔为模数。应县佛宫寺释迦塔之设计可能属中唐以后的设计特点。”[5]173-174肖旻在2002年的研究中指出，应县木塔“塔身+塔基”“塔身+塔刹”可能分别作为整体以“标准高度”（底层檐柱高=第三层外檐总面阔）为模数进行设计，同时塔身高约为塔刹高的4倍[6]。

上述四家的研究形成了一些重要的结论，对笔者在他们的研究思路的基础上继续深入产生了重要的启发作用。

3.2 本次的研究

根据陈明达20世纪60年代的研究，从一层外槽地平到塔刹砖座上皮刚好是6个标准高度（883 cm），同时塔基为这个标准高度的一半[1]46，因此塔身高刚好是塔基高的12倍。无独有偶，笔者在对日本12世纪末之前的楼阁式木塔的分析中发现这一比例关系同时存在于室生寺五重塔和净琉璃寺三重塔中[10]：

室生寺五重塔

塔身高⑦=38.26日本曲尺（1159 cm），塔基高=3.2日本曲尺（97 cm）

塔身高：塔基高=38.26∶3.2≈12∶1

净琉璃寺三重塔

塔身高⑧=33.6日本曲尺（1018 cm），塔基高=2.761日本曲尺（84 cm）

塔身高∶塔基高=33.6∶2.761≈12∶1

4 余 论——模数制的再分析

在张十庆1990年的研究中，对该塔各层的平面尺度也同样采用整数尺的方法进行了分析，同时他还发现各层平面间广同时也是他所找到的基准长N'=44.2 cm的整数倍，但是在我们进行核算时，发现这两组数据都存在着一定的误差（表3）。

表3 应县木塔平面尺度分析（张十庆案）Tab.3 analysis on size of plan in Pagoda of Yingxian Muta (scheme speculated by Shiqing Zhang)

从前文的分析可知，平面尺度设计时很有可能是以第三层总面阔的柱头尺寸为基准，而每上、下一层总面阔递减或递增25“分”，也就是说：

某层总面阔的柱头尺寸

=884±25×1.7n（n=0，1或2）

=1.7×13×5×8±1.7×5×5n

=1.7×5（13×8±5n）

也就是说，每层总面阔基本为（1.7×5=8.5）cm的整数倍，同时每层总面阔的递增或者递减也为8.5 cm的整数倍。于是可以看出，应县木塔的平面总面阔尺寸是以NP=1.7×5=8.5 cm为模数的。

而8.5÷29.46=0.29辽尺，8.5÷44.2=0.19基准长=0.19N'，也就是说这个平面尺度的模数并非整数倍的“辽尺”或“基准长”（N'），即张十庆发现的规律是一个近似的结论。

再来看该塔的高度尺度，很明显在该塔的高度尺寸中A=884 cm是一个基本的模数，其构成如下：884 cm=8×5×13×1.7 cm，同时第四段柱间高为378 cm≈17×13×1.7 cm=375.7 cm，第五层柱高=395 cm≈18×13×1.7 cm=397.8 cm。也就是说高度方向上的尺寸是以NE=13×1.7 cm=22.1 cm为模数的。因此在这座塔中平面尺度和垂直尺度的二级模数是相分离的，但是这两个二级模数之间的数学关系却值得注意：

NP∶NE=平面尺度的二级模数∶高度尺度的二级模数=（5×1.7）∶（13×1.7）=5∶13

结合前引《营造法式》中八棱的记述可知，八棱的边长∶八棱的对边距∶八棱的外接圆直径=5∶12∶13。因此在这座塔中虽然平面尺度的二级模数（Np=8.5 cm）和垂直尺度的二级模数（NE=22.1 cm）相分离，但是它们之间存在着理想的比例关系，而这个比例关系和当时八棱的简便计算公式存在着密切关系。

另外，高度方向的大模数884 cm刚好是8×5×13×1.7 cm，也就是说，大模数A恰好是D=（5×13×1.7） cm的8倍（八边形的边数），而D∶各层总面阔递减值=(5×13×1.7)∶(25×1.7)=13∶5，这也和《营造法式》中所载八棱几何尺度的简便算法的尺度比例关系相一致。同时标准高度=884 cm，恰好是平面尺度二级模数NP=5×1.7=8.5 cm和垂直尺度二级模数NE=13×1.7=22.1 cm最小公倍数D的8倍。

最后NE=22.1 cm≈0.75辽尺，也就是说NP= NE一定不会是整数尺或整数尺的理想倍数，而A=40NE=884 cm=30辽尺。这就说明这套模数系统和整数尺之间存在一定的数学比例关系，此即整座塔的部分尺度呈现整数尺现象的原因。

5 结 语

综合以上可知，应县木塔在创建前必定经过了建筑设计，这个设计由一套模数系统控制。这个模数系统包含三级：大模数A=884 cm（30辽尺）控制着塔总高和标准层总面阔的尺度大小；二级模数N分为平面尺度二级模数NP=8.5 cm和垂直尺度二级模数NE=22.1 cm（0.75辽尺），A为上述两个二级尺度的最小公倍数的八倍，同时NP∶NE=5∶13，这一比例关系准《营造法式》中所载八棱的边长与斜径的比例关系；三级模数a=1.7 cm，相当于“分”值的大小。NP=5a、NE=13a、A=520a。这个尺度一方面控制着构件的尺度大小，另一方面也是对空间尺度进行微调的模数值。

另外通过对应县木塔分高度的分析可以看出，将整个木塔区分为柱高和柱间高的提法是可取的，而普拍方这个构件的断面高统一被归于柱间高的分高度中，这也验证了肖旻对陈明达高度分层方式质疑（2002年）的正确性。

最后应县木塔塔身高∶塔基高=12∶1，这一比例关系同样见于室生寺五重塔（创建于781—793年之间）和净瑠璃寺三重塔（创建于1178年之前不久），因此这一比例关系也许是古代进行楼阁式木塔设计时的手法之一。

注释：

① 陈明达. 应县木塔[M]. 北京： 文物出版社,1966： 26-28. 应县木塔建成于辽清宁二年（1056年）。

② 傅熹年. 日本飞鸟、奈良时期建筑中所反映出的中国南北朝、隋、唐建筑特点[C]//傅熹年. 傅熹年建筑史论文集, 北京： 文物出版社, 1998. 见149-156，158-160和162-165页。药师寺东塔的“分”值为栱厚的十分之一，室生寺五重塔的“分”值为足材广的二十一分之一计。

③ 陈明达. 应县木塔[M]. 北京： 文物出版社,2001： 59. 据陈明达统计，应县木塔每层材栔大小不一，其中使用最多的是25.5 cm×17 cm，则1“分”=25.5÷15=17÷10=1.7 cm。

④ 一般情况下一材两栔=15+2×6=27“分”，而根据后述对应县木塔材栔尺度的分析可知，1栔=6.5“分”，则26“分”恰好是四栔。

⑤ 陈明达. 应县木塔[M]. 北京： 文物出版社,1966： 10. 使用这种标准方材的有：泥道栱、瓜子栱、令栱、慢栱、翼形栱和耍头。

⑥ 张毅捷. 日本古代楼阁式木塔研究[D].上海： 同济大学, 2011： 80-86. 法隆寺五重塔的各层柱间高均为7高丽尺；净瑠璃寺三重塔的柱间高自下向上依次为9.5N和10.5N（N为该塔的基准长）。

⑦ 室生寺五重塔的塔身高和塔基高数据来自奈良県教育委員会奈良県文化財保存事務所, 国宝室生寺五重塔修理工事報告書[M].奈良： 奈良県教育委員会, 1979. 中所载实测数据。

⑧ 净瑠璃寺三重塔的塔身高和塔基高数据来自京都府教育庁文化財保護課. 国宝浄瑠璃寺本堂·三重塔修理工事報告書[M].京都： 京都教育委員会, 1967. 中所载实测数据。