贵州省城市规模分布及异速生长特征——基于分形理论的研究

， ，

(1.贵州师范大学 喀斯特生态文明研究中心， 贵州 贵阳 550001； 2.山东工商学院 工商管理学院， 山东 烟台 264005)

城市体系规模分布的定量分析是城镇化研究中的一项基础性工作。城市规模分布就是城镇人口在不同层级城市的分布，反映了地区城镇化过程，而城市规模和分布结构则直接关系到城镇体系功能的发挥和竞争力的提升。异速生长是城市地理学理论研究中一个非常重要的规律，有助于分析城市的时空演变和等级体系。运用分形理论探讨国内平原地区城市体系的文献已相当丰富，但对“人—地”关系矛盾突出、喀斯特石漠化问题较为严重的高原山区城市体系研究则较为鲜见。贵州是我国典型的喀斯特石漠化地区，造就了不同于其他地区的城市体系和发展过程。故本文选取贵州作为案例地，探讨其城市规模分布规律及城市人口—城区面积的异速生长，这既是对分形理论应用的拓展，又可为贵州未来城镇化路径优化提供理论基础和实践参考。

一、学术背景与研究进展

一般来说，一个地区城市规模的大小，容易直接观察得到，但对一定时期内城市规模的演变特征及其规模分布，则需要充分论证。20世纪以来，国内外学者从经济学和城市地理学的视角对这一系列问题开展了深入研究，针对城市位序—规模有许多具有代表性的观点。而城市规模效益最大化需要有合理的城镇规模分布，因此，城市规模分布的相关研究就显得非常重要。国外学者利用城市分形理论，主要研究城市个体的属性，即其形态、结构、演化机制等问题。B.B.Mandelbrot较早直接运用分形理论来研究城市位序—规模法则的分维数性质〔1〕。M.Batty，A.S.Fortheringham等利用受限扩散凝聚模型(DLA)和电介质击穿模型(DBM)模拟了英国Cardiff市和美国Taunton市的分形生长和空间扩散，开辟了城市模拟研究的新途径〔2～3〕。R.White，G.Engelen利用图式细胞自动机(CA)揭示了城市化过程中空间结构的分形演化及其混沌动力学〔4〕。Frankhouser对全世界主要城市的空间结构进行了分形研究，较为系统地探索了分形理论在城市规模分布中的实践效果〔5〕。自20世纪90年代中期Batty，Frankhouser等分别出版有关“分形城市”研究的理论专著之后，国外的相关成果逐渐减少〔6〕。

在国外分形城市研究进入低潮之际，国内城市地理学分形理论研究崛起。陈彦光等讨论了城市位序—规模问题的分形性质和退化形式，探讨了Zipf定律的理论基础〔7〕；随后，又提出等级规模结构的分形维数及其地理意义〔8〕，并证明了城市体系二倍数规律与位序—规模法则的等价性〔9〕。以分形理论为基础，有学者对地区城市体系规模的分形结构和分形特征、城市人口规模变化规律等进行了实证研究〔10～12〕。孙在宏等借助城市体系位序—规模法则和异速生长定律，对江苏省城市规模分布的相关问题进行了探讨〔13〕。李茂等提出并利用分布偏离度的概念，认为中国城市系统分布偏离度较高，位序—规模分布对中国的情况相对不适用〔14〕。戚伟等借鉴城市位序—规模理论，提出城市流动人口服从类似规律的假设，并对城市流动人口与城市人口位序规模分布进行耦合分析〔15〕。周晓艳等根据2000～2012年我国地级及以上城市的建成区面积数据，利用位序—规模法则及分形理论，对我国城市用地规模分布的变化趋势及不同区域城市用地规模分布变化的差异性进行了研究〔16〕。

已有研究成果不仅印证了分形理论的逻辑科学性，而且还运用分形理论实证探究过区域城市体系规模分布、人口—面积异速生长、流动人口分布等，为研究区域城市体系规模结构及分布提供了有益借鉴。

二、研究方法及数据来源

(一)研究方法

分形理论的探讨对象是自然界和社会活动中无序而又具有自相似性的复杂系统〔17〕。由于分形体系的局部与整体是相似的，分形体系内的局部在一定程度上是其整体的再现和缩影〔18〕。分形是大自然的优化结构，运用分形理论规划城市体系的等级结构，可以优化区域城镇化进程〔8〕。

1.城市规模分布法则

在一个城市体系中，城市与城市之间在功能上的相互依存倾向于导致整个等级体系内部人口规模与其位序之间的特定关系。这种关系就是位序—规模法则，该法则描述了一个国家或区域中的城市规模分布规律。假设一个区域内有若干城市的分布，由于城市与乡镇之间没有明确的界限，设定一个人口尺度r来进行度量〔19〕。当人口尺度改变时，区域城镇的数目N(r)也会相应改变，即当r由大变小，N(r)就由小变大。刘继生等认为当满足下列关系式时：

N(r)∝rD，

区域城镇累积数与人口尺度成负幂律分布，城市规模分布具有分形特征〔20〕。该式为城市规模分布的Pareto公式，类比Hausdorff维数公式，D是分维。可以证明，它与Zipf公式等价〔21〕。Zipf公式为：

P(k)=P1k-q，

(1)

式中k表示城市位序(k=1,2,…,n；n为区域中的城市总数)；P(k)是位序为k的城市人口数；p1为区域最大城市的人口数；q=1/D为Zipf维数，具有分维意义。当q=D=1时，有P1/Pn=n，即最大城市与最小城市的人口数之比恰为整个城市体系的城镇数目，Carroll称此种形态为约束型位序—规模分布〔22〕。当q<1，即D>1时，P1/Pn1，即D<1时，城市规模分布较为分散，城市体系的人口分布差异较大，此时首位城市的垄断性较强。

2.异速生长模型

异速生长，一般理解为“与整个机体的绝对尺寸的变化相关的比例的差异”〔23〕，异速生长定律用于测度生物体的局部与整体的几何关系〔24〕。类比于生物现象，城市地理系统中也会存在这种关系。基于这一思想，Beckmann提出城市体系异速生长方程〔24〕。据Nordbeck的研究，异速生长并不限于刻画系统局部与整体的关系，一个生长体的两个相关变量也可以满足异速生长方程〔25〕。这种观念在后续的研究中得到推广，如城—乡人口关系、人口—面积关系、城市—城市相互作用关系等〔26〕。

因篇幅有限，本文省略异速生长方程的推导过程，该方程的一般形式为：

式中的标度指数αij隐含有维数意义，xi表示要素Pi的某种测度(i=1,2,…,n)，该式具有广义的分形性质。若设xi=A表示城区面积，xj=P表示城区人口，将参数α、β分别用b、a表示，该式可以表示为：

A=apb。

(2)

式中的标度指数b具有维数性质，在早先经过Dutton、Lee等人的实证之后〔27～28〕，Batty， Longley对城市人口—城区面积的异速生长关系作了分形几何学的解释〔29〕。大量的实证观测数据表明，b值处于2/3～1之间，平均值约为0.85〔26，28～29〕。异速生长关系可能会退化，退化实质就是分形结构的退化〔30〕，尽管异速生长的最初定义是幂指数形式，但现实的地理现象还可能退化为指数、对数形式，甚至完全退化为线性关系〔28,30〕。刘继生等认为越接近线性关系，系统的结构越退化〔31〕。

(二)数据来源及说明

本文采用城市城区人口和城市建成区面积作为模型构建的基础数据，数据来源于《中国城市建设统计年鉴(2002～2015年)》，选取贵州省13个城市(贵阳市、六盘水市、遵义市、安顺市、铜仁市、毕节市、兴义市、都匀市、凯里市、清镇市、赤水市、仁怀市、福泉市)作为样本。城区人口是在该区域生活、工作和活动的经常性群体，更能反映城市现实的人口规模。探究一个区域的城市规模，考量的主要对象是城区人口。因此，本文在探究贵州省城市规模分布中，并未选取市区人口或市区非农业人口作为基础数据。建成区面积是指城市行政区内实际已成片开发建设、市政公用设施和公共设施基本具备的区域(《中国城市建设统计年鉴》指标解释)，本文在探究贵州省人口—面积异速生长特征中采用该指标作为城市面积的基础数据。

三、贵州省城镇规模分布

(一)城市规模分布演化规律

据城市规模分布分形性质，城市规模分布一般满足Zipf位序—规模法则。在数理推导中，幂函数关系可以转换为对数线性关系。本文将式(1)两边进行对数转化，利用SPSS 22.0对2002～2015年贵州省13个主要城市的人口规模和位序进行线性关系拟合，即将InPk、InK进行线性回归(结果见图1)。拟合结果显示，2002～2015年模型拟合的决定系数R2的最小值为0.929，表明拟合度较好(见表1)；各年份模型拟合的Sig值均小于0.05，表明线性关系显著。拟合结果还表明，Zipf指数q值均大于1，即D值均小于1，表明全省城市规模分布较为分散，城市体系的人口分布差异较大，首位城市——贵阳市的垄断性较强，在全省城市体系中占据主导地位；但从q值的趋势来看，q值总体逐年在减小，并不断在向理想指数1靠拢，说明全省城市体系的人口分布在逐年趋于均匀化，中间位序的城市在不断发展(见图2)。

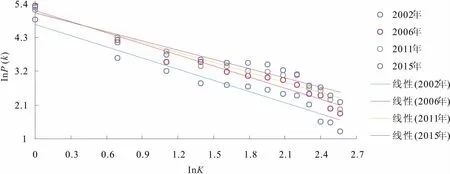
图1 2002～2015年贵州省城市位序—规模双对数坐标关系

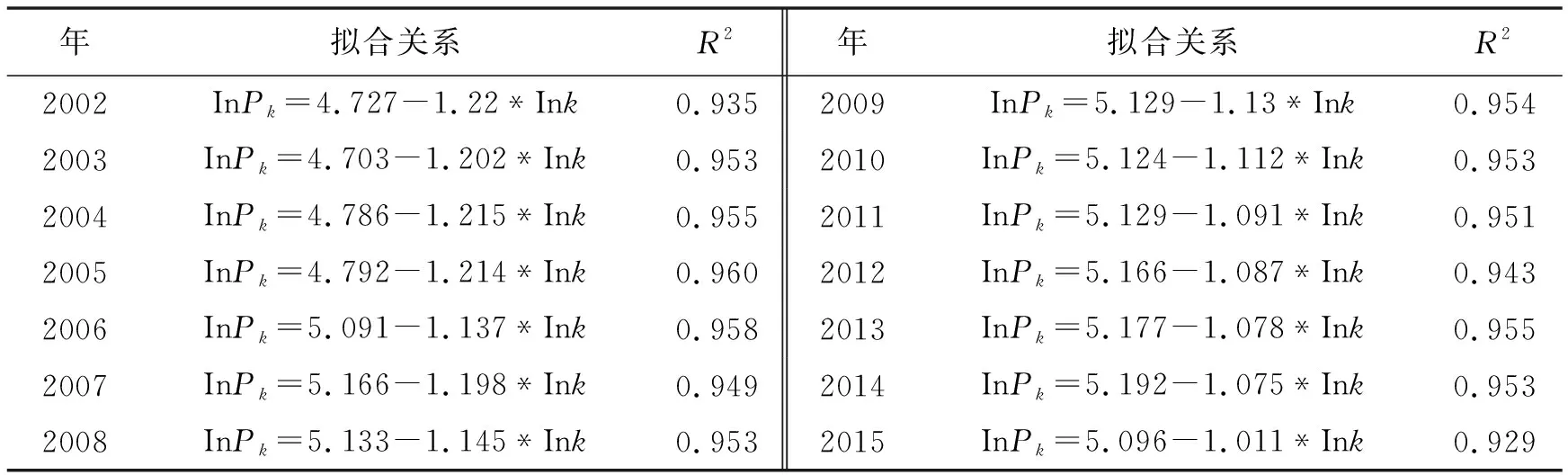
年拟合关系R2年拟合关系R22002InPk=4.727-1.22*Ink0.9352009InPk=5.129-1.13*Ink0.9542003InPk=4.703-1.202*Ink0.9532010InPk=5.124-1.112*Ink0.9532004InPk=4.786-1.215*Ink0.9552011InPk=5.129-1.091*Ink0.9512005InPk=4.792-1.214*Ink0.9602012InPk=5.166-1.087*Ink0.9432006InPk=5.091-1.137*Ink0.9582013InPk=5.177-1.078*Ink0.9552007InPk=5.166-1.198*Ink0.9492014InPk=5.192-1.075*Ink0.9532008InPk=5.133-1.145*Ink0.9532015InPk=5.096-1.011*Ink0.929

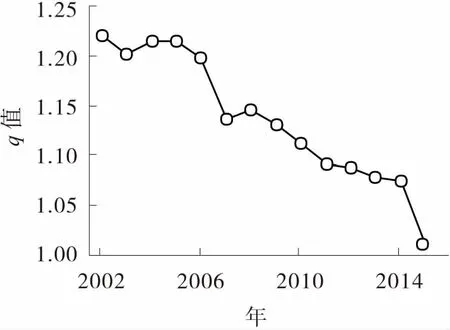
图2 2002～2015年贵州省城市规模分布Zipf指数变化曲线

图2反映了贵州省城市体系Zipf指数的变动轨迹。2002～2015年，q值增减起伏，除了在2004、2008两年有小幅增长外，其余年份的q值均在减小，2002～2015年，q值下降17.13%。“十五”期间，q值维持在高位，减幅仅有0.49%，说明在“十五”期间，全省城市体系规模分布较为分散，城市体系的人口分布差异大，而且向理想值靠拢的速度非常缓慢；“十一五”“十二五”期间，q值向理想值1靠拢的速度比较快，说明在此期间全省城市体系规模分布在快速地均匀化，中间位序的城市在崛起，首位城市的垄断性优势在逐步减弱(见图3)。“十五”期间是西部大开发的开局时期，政策性的影响力还处于“预热”阶段，贵州发达城市首先享受到政策红利，此时城市规模分布的集中力量高于分散力量；“十一五”期间，西部大开发的战略思路得到进一步明确和巩固，公共服务均等化取得新成效，此时城市规模分布的分散力量较为明显；“十二五”期间，尤其在《国务院关于进一步促进贵州经济社会又好又快发展的若干意见》(简称“国务院2号文件”)出台以后，全省走向“后发赶超”的高速发展期，城镇化的战略重要性进一步凸显。贵州省人民政府提出全省高速公路三年建设会战的战略部署，使得全省的资源、资本和劳力逐渐向欠发达城市扩散，城市规模分布的分散力量高于集中力量，城市规模分布的Zipf指数越来越接近理想值，这反映出自然环境和社会环境共同作用于城市体系的演化〔32〕。

图3 2002～2015年贵州省Zipf指数下降趋势

(二)贵州省各城市人口规模演化规律

全省各城市人口规模的演化轨迹，呈现这样一种现象：尽管贵阳市的首位垄断性优势一直处于高位，但中等位序和后位序的城市人口规模发展较快，且其人口规模位序处于不稳定状态。

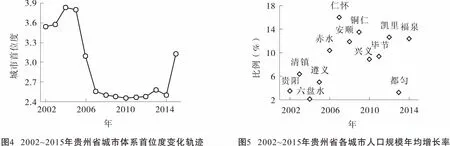
据城市首位度的概念及方法〔33〕，得到图4所示的贵州省城市体系首位度2002～2015年间变化轨迹。2002～2015年，贵阳市首位度的最低值为2.46，按照马歇尔(Marshall)对城市首位度的量化标准〔34〕，贵阳市在全省属于“高度首位分布”。从长期来看，贵阳市的首位垄断性不断受到中等位序及后位序城市快速发展的挑战，表现出城市首位度曲线下滑。

此外，贵阳市、遵义市、六盘水市初始城区人口规模较大的地区，在2002～2015年间人口规模年均增长率比较低；而除都匀市以外的其他中等位序及后位序的城市，人口规模年均增长率都比较高(见图5)。这与图2所示的贵州城市规模分布的Zipf指数在不断变小、并逐年向理想值1靠拢的趋势遥相呼应。

从表2和图6所示的全省各城市人口规模位序的横向对比分析来看，存在两种现象：一是城市人口规模排名前两位的贵阳市和遵义市，与排名后四位的清镇市、赤水市、仁怀市和福泉市，它们的位序比较稳定，其位序的变异数均低于5%，有的甚至为0；二是中等位序的六盘水市、安顺市、铜仁市、兴义市、毕节市、凯里市、都匀市，位序波动比较大，其位序的变异数均在15%及以上。

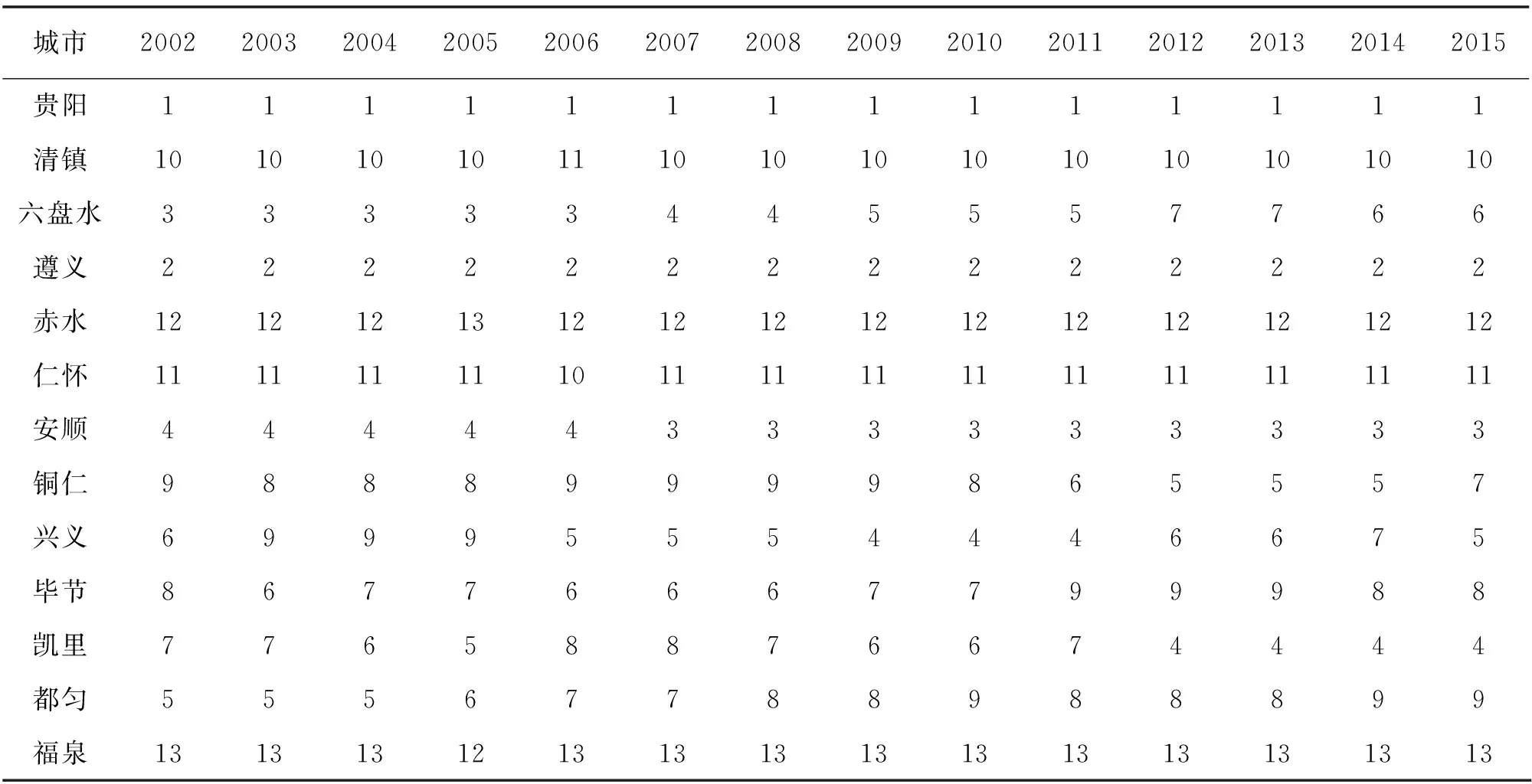
表2 2002～2015年贵州省各城市人口规模位序

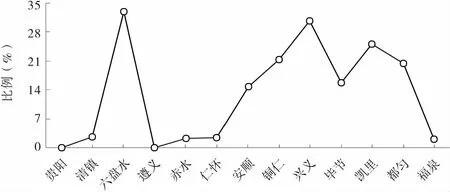
图6 2002～2015年贵州省各城市人口规模位序变异系数对比

另外，贵阳市、遵义市在全省各城市中的垄断性地位还未被撼动，而位序为后四位的城市尽管在2002～2015年间人口规模年均增长率较高，但皆非地级市，其规模发展受到地缘和行政的限制，难以扭转位序靠后的局面。人口规模中等位序的城市整体波动幅度较大，参差不齐，有三种表现：一是城市人口规模增速较快，如铜仁市、凯里市、兴义市，其城市规模位序在波动上升；二是城市人口规模发展缓慢，其位序下降，如六盘水市和都匀市；三是城市人口规模发展平稳，位序几乎保持不变，如安顺市、毕节市。这表明，在全省城镇化的战略推动下，中等位序的城市既迎来了发展机遇，但在经济、社会和环境方面又避不开结构性调整的问题，在这些因素的综合影响下，城市在发展的过程存在着一段“缓冲期”和“适应期”。

四、贵州省城市人口—面积异速生长特征

(一)全省人口—面积异速生长模型

城市用地形态已被证明具有分形结构，城市系统的异速生长与分形演化具有密切的梳理关系〔29〕，异速生长定律适用于描述城市人口—建成区面积的关系〔30〕。在异速生长的模型推导中，由于异速生长的原始定义表现为幂指数形式，而现实中的地理现象并非始终坚持服从幂指数规律，若幂函数的拟合优度小于其他曲线的拟合优度，则两者的异速生长关系退化。表3和图7显示，全省城市人口—面积异速生长关系整体上已有退化的现象，直接表现为幂函数拟合优度整体小于线性拟合优度。

表3 2002～2015年贵州省人口—面积异速生长拟合模型

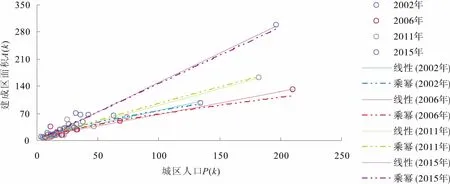
图7 2002～2015年贵州省人口—面积异速生长线性和幂函数拟合关系

退化迹象表明全省城市体系整体性在减弱，这可能与全省城市体系尚未形成理想的规模序列结构、首位城市的强势垄断以及资源分配过于集中于少数城市等因素有关。另外，全省大多数城市的人口—面积异速生长关系表现出以指数函数拟合较高的半退化形式，并且除个别城市以外，其他城市的人口—面积异速生长模型拟合优度都不高(见表4)。这说明全省大多数城市的发展还存在一定的盲目性，人口规模与建成区面积之间的关系规律性不明显，城市发展存在诸多不协调因素。

(二)贵州省城市体系人口—面积的异速生长关系分析

城市“人—地”的异速生长关系具有幂函数关系，可以用标度指数来解释。如前所述，式(2)的标度指数b表示异速生长关系，具有维数性质。关于人口—面积异速生长关系的维数，学界存在争议：有学者认为两者之间具有二维的地理意义〔29〕；有学者认为，类比于生物发育的“表面—体积”约束，城市面积是二维变量，人口是三维变量〔27〕；还有学者认为，式(2)就已经隐含了三维空间的思想〔26〕。当b<1时，人口增长速度比城区面积增长速度快(文中称为负异速)，城市向高层纵向发展，此时除了增加建筑物的密度以外，就是增加建筑物的高度；当标度指数b=1时，城市人口数量与城区面积同速变动，城市高度没有变化；当b>1时，人口增长速度比城区面积增长速度慢(文中称为正异速)，城市向扁平化横向发展。

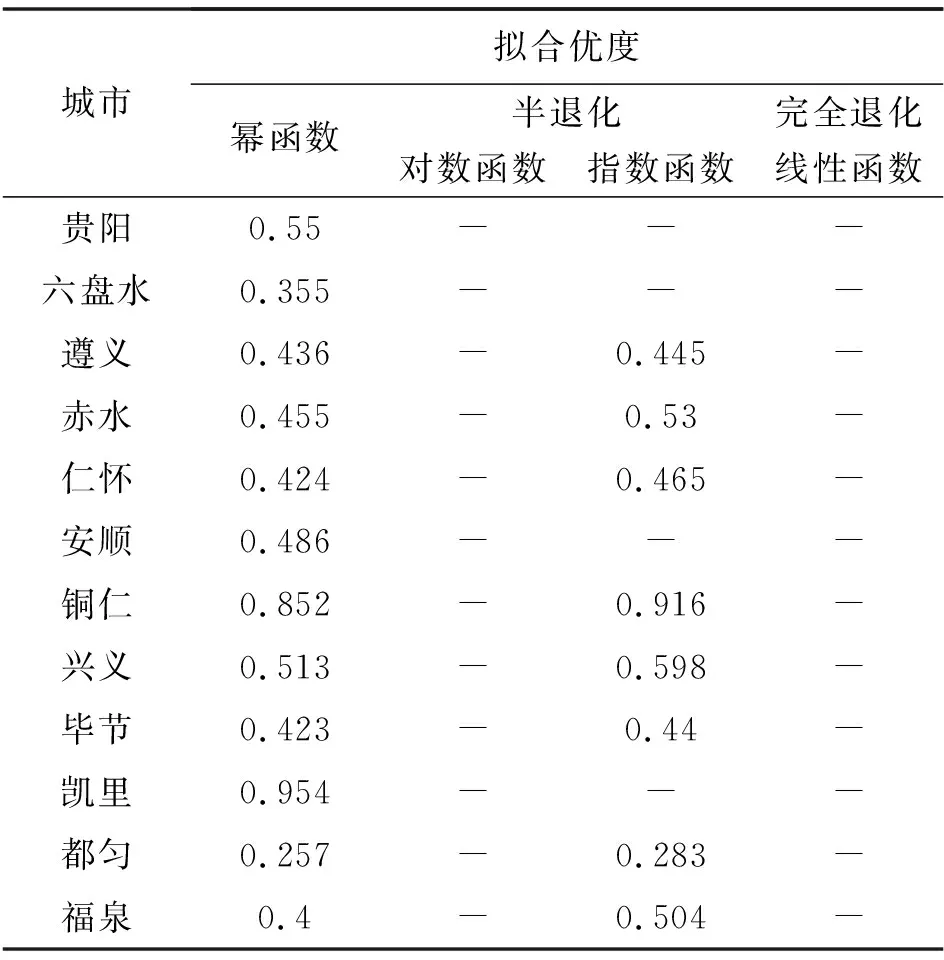
表4 贵州省各城市人口—面积异速生长模型拟合优度比较

人口—面积异速生长关系的维数之争，不是本文的研究目的，因而不做详细考究。就标度指数b的合理性而言，b<1符合发达城市的普遍法则〔13〕，即城市人口越多，在城市面积扩张受限的情况下，城市越向纵向的高层发展。

据表5，全省城市人口—面积异速生长的标度指数平均值为0.8515，与前文所述标度指数的经验平均值0.85相当；且标度指数整体呈现逐渐增长的趋势，两者之间由负异速转变为正异速，尽管在2014年该指数有所回落，但回落的幅度不大，仍然接近1。而拟合优度更高的线性拟合的系数同样如此，只是由负异速转为正异速的时间节点比幂函数拟合的标度指数早一年。由此可见，全省城市人口—面积之间正异速生长是城镇化发展中的一个重要趋势。即近年来，全省在城镇化的过程中，城市面积的增长速度比人口要快，表现为城市面积在扩张，城市是扁平化的横向发展。

表5 2002～2015年贵州省城市体系人口—面积异速生长系数及其关系演化

无论是幂函数拟合，还是线性拟合，全省城市人口—面积异速生长关系的转折节点都在2012年(见表5)，这个时间节点不难解释。2012年1月12日，针对贵州发展的国务院2号文件出台。文件指出，贵州要“大力实施工业强省和城镇化带动战略”。在城镇化战略的带动下，贵州城镇化表现为城市空间扩张为先，再产生集聚的城镇。换言之，当前贵州城市人口—面积正异速生长关系是未来人口集聚的前提和基础。由于贵州还处于城镇化的建设期，人口—面积正异速生长关系维持在何种水平为合理，并将持续多久，还需要进一步的观察和探讨。

五、结论及讨论

本文探讨了贵州省城市体系规模分布及城市人口—面积异速生长特征，得到下述结论：

(1)贵州省城市规模分布较为分散，贵阳市在全省仍属于高度首位分布，但从整体趋势来看，中等位序及后位序的城市崛起速度较快，城市规模分布的集中力大于分散力，城市体系规模分布的Zipf指数逐年向理想值1靠拢。

(2)全省城市人口整体增长，但不同城市增幅有所不同，大城市和小城市的人口规模序列比较稳定，中等城市人口规模位序有增有减。从空间分布来看，贵阳、遵义、都匀、凯里、安顺、毕节等黔中经济区的城市是全省城市人口规模增长的中坚力量，贵阳市、遵义市的人口增长仍然是贵州人口城镇化的主要拉力。

(3)全省城市体系人口—面积的异速生长整体上存在退化现象，城市体系整体性呈现减弱。此外，除铜仁市和凯里市以外，其他城市的人口—面积异速生长模型拟合优度不高，表明在城镇化的过程中全省大多数城市人口规模增长与建成区面积之间具有“无律”性特征，两者之间协调度较差，人力资源和地理空间资源未能得到有效开发；且全省人口—面积异速生长关系由负向正转变，城市面积增长速度快于人口增长。

贵州省城市体系规模分布的Zipf指数q均大于1，即D均小于1，城市规模分布由分散向集中过渡，这与平原地区的浙江省和江苏省Zipf指数q演化规律相反〔10,13〕。而不同类型地域空间的城市体系规模分布的演化方向是否相反，以及造成这种相反演化规律的原因，值得学术界进一步深入探讨。本研究选取贵州省13个城市作为样本，研究的空间尺度相对较大，未来可以缩小空间尺度，将范围扩大至县域城镇，更能全面地摸清贵州省城镇规模分布的规律和人口—面积异速生长的关系。