我国PPI与CPI正向传导与反向倒逼机制分析

张小宇，刘永富

（吉林大学a.数量经济研究中心；b.商学院，长春 130012）

0 引言

对于测度生产领域价格水平的PPI指数和测度消费领域价格水平的CPI指数，一直以来深受经济学者和货币政策部门的高度关注。然而，有关PPI和CPI二者的影响机制和传导渠道，无论是理论层面还是实证层面均存在显著的争议。因此在我国经济发展处于新常态的特殊阶段、经济政策调控由需求侧刺激转化为供给侧结构性改革的关键时期，厘清PPI与CPI之间的动态传导机制不仅影响着供给侧结构性改革的实施，也影响着货币政策调控模式的选择。近几年我国价格传导机制出现了一些新的特征，一是PPI与CPI指数整体水平不断上涨；二是PPI涨跌幅度远大于CPI的涨跌幅度；三是二者间的关联弱化甚至出现“正负背离”[1-3]。传统的价格传导理论侧重于供给冲击的角度分析问题，认为上游价格（PPI）向下游价格（CPI）传导，即PPI是CPI的先行指标[4-6]。PPI向CPI传导的途径主要有三种：PPI（煤炭、成品油、电力）→农业生产资料→CPI；PPI（采掘业）→水电燃料→CPI；PPI（原料加工、加工工业）→工业消费品→CPI。基于需求视角的研究则认为下游价格（CPI）向上游价格（PPI）传导，即CPI是PPI的先行指标[7-9]。其传导路径为CPI的变化通过引致需求和生产成本传导至PPI。另外，近几年也有学者发现PPI与CPI的作用机制出现了双向传导的途径[10，11]。

尽管上述众多文献对我国PPI与CPI的动态传导机制、现实的静态关联进行了大量的理论分析和实证研究，但均缺乏对二者之间的关联机制随时间推移以及在经济周期不同阶段下的动态演化机制的分析。鉴于此，本文通过构建滚动视窗动态相关系数以及滚动视窗Granger因果关系检验统计量对我国PPI与CPI之间的动态演化机制进行实证检验，以期给出现阶段我国PPI和CPI是否出现背离、PPI和CPI是正向传导还是反向倒逼的清晰判断，为供给侧结构性改革和需求侧货币政策调控给出明确的政策建议。

1 PPI与CPI相依性的动态演化机制检验

关于PPI与CPI之间的关联机制，无论从正向传导还是反向倒逼理论，无论从短期冲击还是从长期均衡视角，均认为二者之间应存在显著的正向相关关系。然而，随着时间的推移，商品生产方式的转变，商品流动链条的优化，商品定价机制也将随之发生改变。因此在经济周期的不同阶段，PPI和CPI之间的动态相关关系也会发生改变，这不仅表现在二者之间传导机制的转变，也可能出现相关关系强弱的变化。为考察二者之间相依性的上述时变特征，本文拟构建滚动视窗动态相关系数进行识别和检验。设x和y分别表示PPI和CPI，则x和y的滚动视窗动态相关系数可表示为：

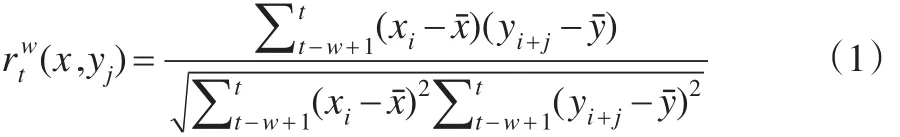
其中，j=0，±1，…，±d表示计算动态相关系数时变量x和y的滞后和超前阶数，d为最大超前和滞后阶数。w为视窗宽度，考虑到视窗宽度太小将影响动态相关系数的稳定性，因此本文视窗宽度设定为180，对应样本时间跨度为15年①本文也尝试更改视窗宽度，适当增加和减少w的取值，结果发现更改视窗并不影响本文的结论。。

为了计算上述动态相关系数，选取1996年10月至2017年1月生产者价格指数和消费者价格指数①由于生产者价格指数能够获得的最早数据为1996年10月，故本文样本数据的起始时期设定为1996年10月。，见图1和图2所示，数据来源于中经网统计数据库。

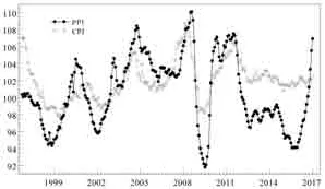
图1 PPI与CPI指数曲线图

从图1给出的PPI与CPI指数曲线可以看出，我国PPI与CPI的波动模式是一致的，但也存在一定的差异。首先，与CPI相比，PPI波动幅度更大，这一点从PPI和CPI序列的样本标准差也可清晰地反应出来，其中PPI序列的样本标准差为4.2，而CPI序列的样本标准差为2.3；其次，随着时间的推移，特别是现阶段，我国CPI与PPI出现了背离的倾向。吕捷和王高德（2015）[2]构建三部门动态随机一般模型研究了CPI与PPI相背离的结构性原因，并且定性和定量地考察了货币冲击对CPI与PPI的影响。研究发现，当正向的货币冲击来临时，因为劳动力由基础农业部门向基础加工服务部门流动，基础农业部门逐渐收缩但加工服务部门逐渐扩大，这种结构性变化导致基础农产品价格下降，基础工业品价格经过短暂上升后持续下降，而加工服务部门生产的最终消费品价格不断上升，导致CPI与PPI出现了背离的倾向。

利用1996年10月份至2017年1月份数据，计算出PPI与CPI滚动视窗动态相关系数，最大超前滞后阶数d设定为2，并按照超前和滞后阶数的不同分别绘制了动态相关系数曲线，如图2所示。

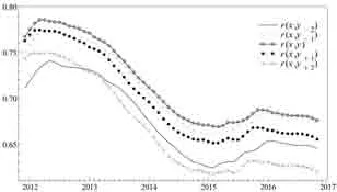
图2滚动视窗动态相关系数

从滚动视窗动态相关系数的计算结果可以看出，随着时间的推移，我国PPI和CPI序列相依性逐渐降低，无论是PPI与滞后CPI、PPI与超前CPI，还是PPI与同期CPI的动态相关系数，均具有递减的趋势（尽管近两年该趋势趋于平缓）。

2 PPI与CPI动态传导机制分析

为进一步考察我国PPI和CPI相依性的动态转变特征，本文构建了包含PPI和CPI的P维二元向量自回归模型：

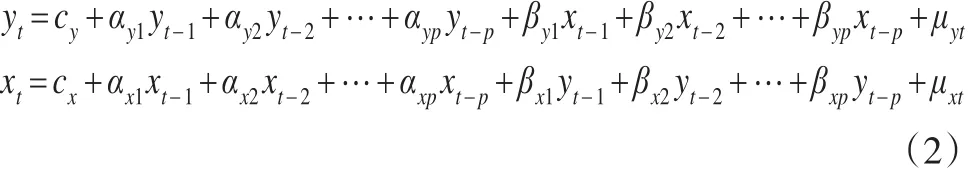
x和y仍然表示PPI和CPI，ci、αij、βij，i=x，y，j=1，2，…，p为模型回归系数，μit～i.i.d.N(0，σ2i)，为扰动项。对于上述向量自回归模型，如果βy1=βy2=…=βyp=0，表明xt的滞后值不能为预测yt提供任何信息，因此称xt非 Granger影响yt。同理，如果βx1=βx2=…=βxp=0，表明yt的滞后值不能为预测xt提供任何信息，因此称yt非Granger影响xt。对于上述向量自回归模型，若检验xt非Granger影响yt，可以通过估计式（2）中的第一个方程，构建拉格朗日乘子检验统计量进行检验：

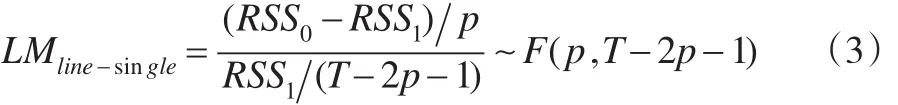
RSS1是式（2）中第一个方程的残差平方和，RSS0为该方程约束回归的残差平方和，T是样本容量。LMline-single检验统计量服从F分布。上述检验方法被称为Granger因果关系的单方程检验方法。Bewley(1986)[12]认为Granger因果关系的单方程检验方法通常单独估计系统方程中包含内生变量的结构式方程，存在随机解释变量问题，导致模型的参数估计量是有偏的或非一致的，进而影响Granger因果关系检验的结果。为克服上述问题，应采用系统检验方法，即将向量自回归模型作为一个系统同时估计。构建的检验统计量为：

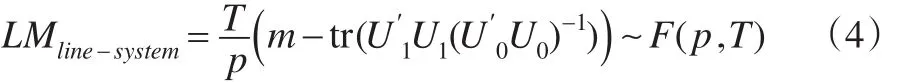
m为系统方程组中结构方程的个数，tr(·)为矩阵的迹，U1是系统方程残差矩阵，U0则为约束的残差矩阵。LMline-system渐近服从自由度为(p，T)的F分布。

为考察我国PPI和CPI之间的传导机制是否发生了结构性变化，本文采用系统检验方法，对PPI和CPI序列进行了滚动视窗的Granger因果关系检验，按照AIC、SIC信息准则，向量自回归模型中内生变量的滞后阶数设定为3，对应为1个季度②为避免因非平稳时间序列建模导致伪回归问题，本文对PPI和CPI序列进行了单位根检验，检验结果表明无论是采用ADF单位根检验、PP检验还是采用KPSS检验，上述序列均不包含单位根，为平稳时间序列，检验结果略。。与计算滚动视窗的动态相关系数一致，滚动视窗的Granger因果关系检验中视窗宽度同样设定为180。

图3给出了基于系统估计的我国PPI和CPI之间的滚动Granger因果关系检验结果，图中两条曲线分别基于系统估计得到的Granger因果关系检验拉格朗日乘子统计量（LM统计量）对应的显著性概率（即P值）序列。

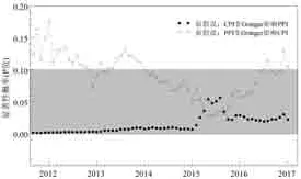
图3滚动视窗Granger因果关系检验显著性概率

从滚动视窗Granger因果关系检验显著性概率曲线图可以看出，在全部视窗内，基于系统估计的Granger因果关系检验统计量均能在5%的显著性水平下拒绝CPI非Granger影响PPI的原假设，表明在全部视窗内我国PPI与CPI的反向倒逼机制是成立的。而对于PPI与CPI的正向传导机制检验（即检验PPI非Granger影响CPI），在滚动视窗的前半部分，即2014年之前（个别样本视窗除外），对应的检验均不能在10%的显著性水平下拒绝PPI非Granger影响CPI的原假设；在滚动视窗的后半部分，即2014年之后（个别样本视窗除外），相应的LM检验统计量对应的显著性概率均小于10%，这表明此阶段我国PPI与CPI的正向传导机制是有效的。上述实证检验结果表明在滚动视窗的前半部分，我国PPI与CPI动态传导机制中只有反向倒逼机制是有效的，而在滚动视窗的后半部分，PPI与CPI的正向传导和反向倒逼机制均是有效的。

3 结论

本文通过构建滚动视窗动态相关系数对我国PPI与CPI之间的动态相依性进行了检验，在此基础上，通过构建基于系统估计的滚动视窗Granger因果关系检验，对我国PPI与CPI之间的传导机制及其时变特征进行了识别，得到如下结论：

（1）尽管我国PPI与CPI总体波动模式还比较相似，但波动幅度已出现异化，特别是近期PPI与CPI出现了背离的趋势。美国次贷危机之前我国PPI与CPI序列无论在趋势上、波动模式上，还是波动幅度上都十分相近。这为利用生产要素与消费品价格的协同变动趋势预测通货膨胀提供了思路。然而随着我国对外开放水平的不断提高，生产要素市场和商品市场受国际市场冲击的影响日趋严重，这意味着过去在相对封闭条件下考察PPI与CPI的传导机制已不再适用，必须在开放经济视角下考察二者之间的复杂传导关系。

（2）我国PPI与CPI之间的相依性正逐渐减弱。通过计算滚动视窗的PPI与CPI动态相关系数，发现无论是同期相关系数、PPI与CPI超前期以及PPI与CPI滞后期的相关系数均随着时间的推移而减小，这与现阶段我国PPI与CPI走势出现分化的事实一致。

（3）我国PPI与CPI的传导机制发生了由反向倒逼单驱动阶段变为正向传导与反向倒逼双驱动阶段的结构性转变。因此现阶段对通货膨胀进行调控时，除利用货币政策的需求管理方法之外，还可采用基于供给侧的价格管制方法实现消费品价格稳定、通胀温和的目标。