塔里木河生态水流情势分析及其适应性利用
杨 帆,薛联青,,3,张洛晨,杨昌兵,魏光辉,陈新芳
(1.河海大学水文水资源学院,江苏 南京 210098; 2.德克萨斯大学奥斯汀分校水文地质系,美国 奥斯汀 TX78705;3.河海大学文天学院,安徽 马鞍山 243000; 4.新疆塔里木河流域管理局,新疆 库尔勒 841000)
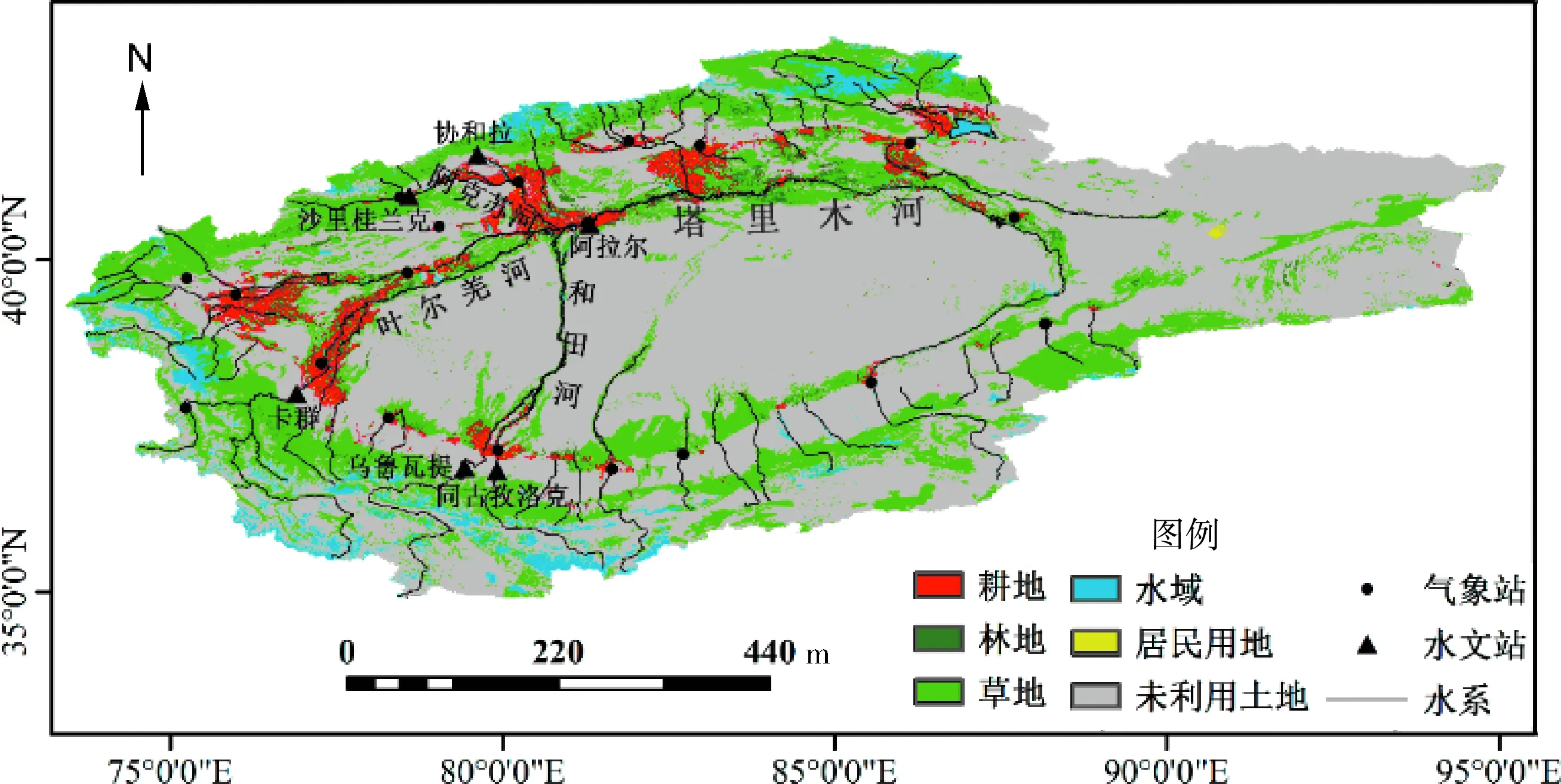
图1 2015年塔里木河流域植被覆盖及水系
引水灌溉、筑坝蓄水等水资源开发利用行为所引起的自然水流情势改变,是导致许多河流生态问题的主要原因之一[1-3]。生态水流适应性利用是指在保证河流生态系统良性循环的前提下,在水资源开发利用过程中考虑人类活动、气候变化、陆面变化等环境变化对水文过程的影响,调整水文过程以适应生态变化的水流利用模式[4]。生态水流适应性利用概念的提出正是为了缓解河流水资源开发利用与生态环境保护的矛盾。国内外学者对生态水流的理论研究从最早阶段的最小保证生态需水量[5],到在不同季节或不同月份维持阶梯式变化的标准流量[6],再到形成一种具有季节性涨落变化的动态水文过程[7]。随着河流水文、水质、泥沙和生物研究的深入,基于生态-水文响应关系的生态水流评估得到广泛关注[8-9]。Wang等[10]采用整体法针对单项生态目标分别建立了水文指标与生态指标之间的量化关系, 结合生态保护目标和人类需水综合估算了环境水流。薛联青等[11]采用改进的变化范围法定量评估了水库兴建对下游河流生态水文情势的影响。这些生态水流评估研究一般假设自然水流情势是生态水流的最佳状态[12],然而,近几十年来,气候和下垫面条件的变化已经导致生态水流情势发生显著改变,鉴于此,生态水流情势的适应性利用应基于相似的动态水流变化基础,并且有必要重新确定水资源开发利用的理想水流状态[13]。本文以干旱区塔里木河流域为研究对象,从不同水平年的角度分析源流及干流的生态水流情势,基于逐步回归和自回归滑动平均的组合回归模型,构建适应于生态变化的不同利用方式的水流变化方程,以期为流域构建适宜的生态水文条件及水资源适应性利用提供科学参考。
1 研究区概况
塔里木河流域位于东经73°10′~94°05′,北纬34°55′~43°08′,总面积102万km2,是我国第一大内陆河流域[14]。受高山环绕影响,塔里木河流域形成了典型的大陆性干旱气候,具有降水稀少、蒸发强烈、昼夜温差大的气候特征。流域多年平均地表径流量为398.3×108m3,干流区径流补给主要来源于阿克苏河(73.2%)、和田河(23.2%)及叶尔羌河(3.6%)。塔里木河流域以水养农业经济为主,经济发展高度依赖水资源分布。随着流域内工农业生产的发展和人口的不断增加,流域生态水文过程变化显著,尤其是20世纪70年代以来,塔里木河干流下游长期断流,生态环境严重恶化。2015年塔里木河流域植被覆盖及水系情况见图1。
2 研究方法
2.1 生态水流情势分析方法
在生态水流情势分析中,一般采用滑动T检验法[15],在此不做详细介绍。根据GB/T50095—98《水文基本术语和符号标准》,利用P-Ⅲ频率分析法确定源流及干流水文过程的统计参数和各频率设计值,采用对应10%、25%、50%、75%、90%的保证率作为划分径流量丰、平、枯水年的标准[16]。
2.2 组合回归模型
选择ARMA(auto-regressive and moving average)模型和组合回归模型进行对比分析,从而确定组合模型与单个模型在塔里木河流域的适用性。根据生态水文过程的水量平衡关系,源流来水量一般由河道渗透量、生态变化天然补给量、生态变化周期性水量和生态变化随机性水量组成,而地表径流量为源流来水量与河道渗透量的差值,表达式为
L(t)=S(t)+T(t)+P(t)+R(t)
(1)
X(t)=L(t)-S(t)
(2)
式中:L(t)为源流来水量;S(t)为河道沿程渗透量;T(t)为生态变化天然补给量,表示水文过程因水文或气象因素引起的季节性或多年变化趋势;P(t)为生态变化周期性水量,表示水文过程按年、月等呈现的周期性变化;R(t)为生态变化随机性水量,表示临时性、偶然性的因素引起水文过程的随机变化水量;X(t)为地表径流量;t为时间变量。
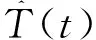
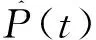
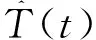
2.2.1T(t)的分离方法
借助SPSS19.0软件,采用非平稳序列逐步回归分析法选择水文过程的预报因子,对预报因子进行统计检验,若所有回归系数为0的假设不成立,则能够认定该水文过程存在T(t);反之,该水文过程不存在T(t)。T(t)是预报对象和预报因子之间的函数。对于剔除渗透量后的地表径流过程,T(t)的近似值可表示为
T(t)=b0+b1t+b2t2+b3t3+b4t4+b5t-1+
b6t-2+b7t-1/2+b8t1/2+b9et+b10lnt
(3)
式中b0、b1、…、b10为系数。
逐步回归模型将时间变量t组成的t、t2、t3、t4、t-1、t-2、t-1/2、t1/2、et、lnt等作为预报因子,年径流量序列作为预报对象,回归计算中对预报因子进行筛选,在信度α=0.05时选择预报因子,直到引入所有合格的预报因子,回归结束,计算各被选变量的回归方程及模拟精度。若方程对应的显著性水平小于0.05,可以拒绝原假设,表明回归方程预报因子整体上对预报对象有显著性的线性影响,回归方程显著。
2.2.2P(t)的分离方法
将X(t)剔除T(t)后的序列作为P(t)的预报序列y(t)。y(t)依次按长度l(2≤l≤m)进行分组:
(4)
式中:n为原序列样本长度,n0为满足i+(n0-1)l≤n的最大整数,m=int(n/2)。对各组求平均,则得到一个长度为l的平均值序列,称之为长度为l的试验周期序列。按不同长度分组为(m-1)个试验周期序列。将各试验周期序列按其周期性外延,时期长度为n,并将这m-1个新序列视为因子x1、x2、…、xm。则回归方程P(t)可以表示为
(5)
式中:i为周期数,i=2,3,…,m;t为时间(t=1,2,…,n)。利用逐步回归方法,对x1、x2、…、xm-1进行变量的引入和剔除,直到既无变量可剔除又无变量可引入为止,记下被选变量的序号i。计算各被选变量的回归方程及模拟精度。若方程对应的显著性水平小于0.05,可以拒绝原假设,表明回归方程预报因子整体上对预报对象有显著性的影响,回归方程显著。
2.2.3 利用ARMA模型的R(t)分离方法
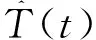
R(t)=φ0+φ1yt-1+φ2yt-2+…+φpyt-p+
εt-θ1εt-1-θ2εt-2-…-θqεt-q
(6)
式中:φp为自回归模型的系数;θq为滑动平均模型的系数。
2.2.4 模拟精度评价标准
根据水文情报预报规范(GB/T 22482—2008)中长期预报精度评价方法,当一次预报的误差小于许可误差(20%)时,视为合格[18]。合格预报次数与总次数的百分比为合格率,表示预报总体精度水平。预报项目的精度按照预报合格率的大小分为3个等级。合格率超过85%为甲等;合格率在70%~85%为乙等;合格率在60%~70%为丙等。预报精度达到甲、乙两个等级者,可用于发布正式预报;精度达到丙级者,可用于参考性预报; 精度丙级以下者,只能用于参考性估报。
注:滑动T检验中,P<0.01表示特别显著变化; ↑*(↓*)P<0.05表示显著上升(下降); P≥0.05表示变化不显著。图2 塔里木河源流及干流径流变化过程
3 塔里木河生态水流情势分析
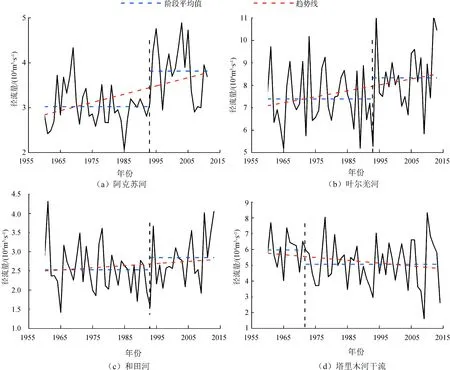
水流情势是河流生态过程的重要驱动力, 水流季节性涨落、年际变化过程与河流水质、泥沙及水生生物的更替过程之间存在着天然匹配的契合关系[10]。图2为1960—2011年塔里木河源流及干流径流变化过程。由图2可知,源流和干流的径流年际变化趋势不一致,总体上源流来水量呈增加趋势,干流来水量呈减少趋势。采用滑动t检验对源流及干流年径流变化趋势进行检验发现,源流地表径流在1993年前后变化明显,阿克苏河、叶尔羌河和和田河的趋势系数分别为0.018×108m3/a(p<0.01)、0.027×108m3/a(p<0.05)和0.006×108m3/a(p=0.12),呈现增加趋势。干流地表径流在1972年前后变化显著,趋势系数为0.018×108m3/a(p<0.05),呈现减少趋势。1960—2011年区间耗水量呈增加趋势,最主要原因可能与源流区农业灌溉面积扩大和无序开挖引排等有关。随着塔里木河流域气候在20世纪80年代开始明显地“增暖变湿”[19],源流区地表径流呈现不同程度的增加,但由于人类活动规模和强度的持续增加,干流生态环境逐渐退化。2000年以后,流域生态环境在各项治理措施的实施下有所改善,但仍然处于极其脆弱的局面。
流域生态状况与自然水文过程是可自由流动河段生态水流情势评估的参考。根据1960—2011年塔里木河源流及干流的水文频率曲线,查得10%、25%、50%、75%和90%对应的径流量,并计算出不同频率对应的源流区间耗水量(表1)。由表1可知,随着保证率的增加,源流区间耗水量呈减小趋势。当源流来水频率小于50%(偏丰)时,干流径流的增加幅度小于源流,源流区间耗水量的增加幅度较为明显,这是由于丰水期源流地表水资源被大量灌溉引水利用,以及河道漫溢、水面蒸发等加剧导致水流损耗严重;当频率大于50%(偏枯)时,干流径流的减小幅度小于源流,区间耗水量减小幅度较为平缓,这是由于在枯水期,管理措施的实施保障了流域水资源的空间均衡,与已有研究结果一致[20]。
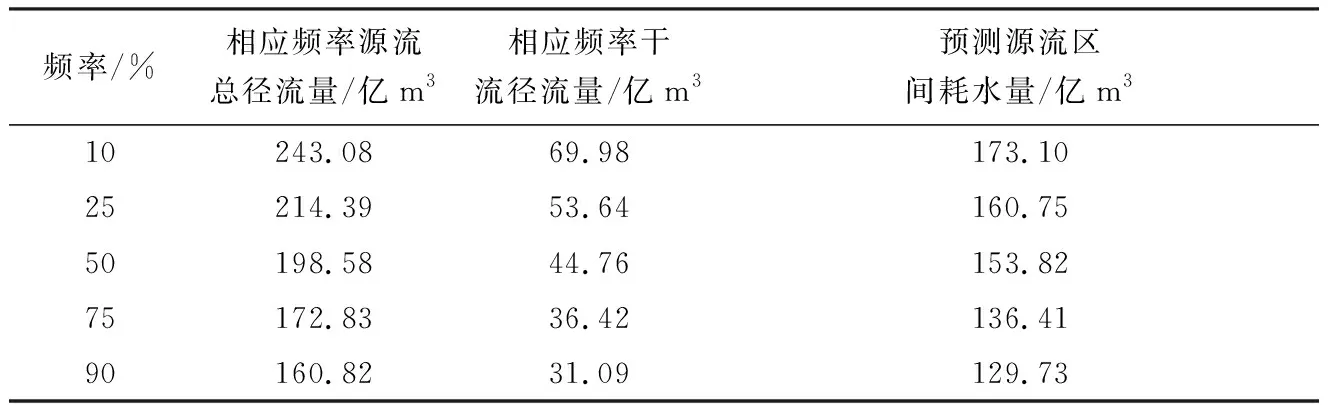
表1 不同频率下源流区间耗水量的预测
图3为塔里木河1960—2011年源流及干流的年径流丰枯变化过程,可见源流区水文过程呈现显著的“由枯转丰”的趋势,干流区水文过程呈现“由丰转枯”的趋势。结合表1的耗水量数据,预测未来一段时间,源流区间耗水量仍保持的明显的增加趋势。可依据生态水流情势特征,开发适宜的生态功能区,如高流量过程适合于乔木类植物生长和生物的繁殖与迁徙,低流量过程有利于灌木、草地的生长和生物越冬。
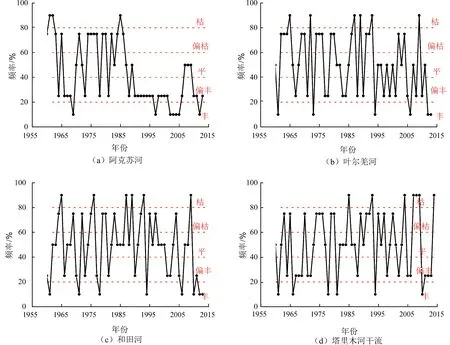
图3 1960—2011年塔里木河年径流丰枯变化过程

河流名称b0b1b3b4b5b6b10相关系数统计量显著性水平阿克苏河-82287.5-7903.95.4-0.1155341.8-36673.576590.00.7779.5810叶尔羌河-518694.5-17596.76.9-0.11189403.9-575698.1282662.60.3811.0650.402和田河-310594.0-9692.43.60.0695332.2-346012.6158345.80.4972.0630.068塔里木河干流-346583.4-14305.26.7-0.1815811.1-397146.2201885.50.4221.3580.247
4 生态水流适应性利用分析
当前生态调度遵循总量控制原则,在水资源长期匮乏的干旱区适用性较差,而生态水流适应性利用无疑是一种更有效的生态调度方式。生态水流适应性利用是根据不同水平年的生态水流的周期、趋势和洪峰低谷等变化特征,在时间上和空间上实行定期和不定期水量分配,从而更有效的利用有限的水资源。因此,生态水流适应性利用是适应环境变化和保障水资源系统良性循环的水资源利用方式。
针对塔里木河流域源流及干流年径流序列,将研究时段分为率定期(1960—2000年)和检验期(2001—2011年),分别采用ARMA模型和组合回归模型进行适应性的对比分析。ARMA模型直接对生态水流序列进行预测,而组合回归模型将流域生态水流按照不同利用方式分为生态变化天然补给量T(t)、生态变化周期性水量P(t)和生态变化随机性水量R(t)进行预测。
4.1 T(t)的预测
利用前文中介绍的方法建立T(t)方程,方程对应的回归系数、相关系数、统计量和显著性水平见表2。图4为径流量实测值与T(t)的变化过程,由图4可知,源流的T(t)呈增加趋势,干流的T(t)呈减少趋势。这是由于20世纪80年代以来,新疆气候持续变暖,温度升高引起冰川融雪补给的径流量增加,而干流径流呈不显著的减少趋势,说明人类活动的增强已影响到干流T(t)的变化过程。
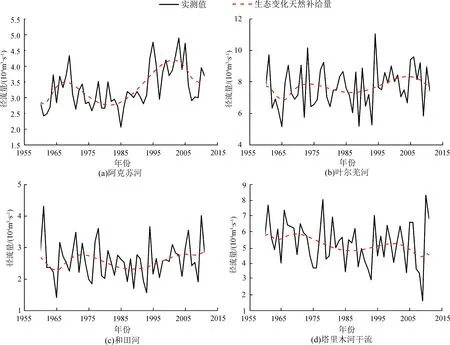
图4 径流量实测值与T(t)变化过程

流域名称P(t)方程相关系数统计量显著性水平阿克苏河P^1(t)=-2483.42+0.16x2,t-0.015x3,t+1.16x7,t-4.34x17,t0.59617.3210 叶尔羌河P^2(t)=-88.25-0.004x3,t+0.344x8,t-0.21x9,t-1.21x17,t0.39232.2850.071和田河P^3(t)=-38.2+2.03x7,t-12.49x13,t+2.01x17,t0.31525.8170.033塔里木河干流P^4(t)=-2210.2-0.10x3,t-1.15x9,t-0.165x17,t0.45220.2470
4.2 P(t)的预测
根据前文介绍的方法分别得到源流及干流的P(t)方程及相应方程的相关系数、统计量和显著性水平(表3)。由表3可知,阿克苏河、叶尔羌河、和田河和塔里木河干流对应的生态水文过程周期分别为2、3、7、17年、3、8、9、17年、7、13、17年和3、9、17年。根据生态水流的周期变化特征,制定不同地区的定期水量配置方案,即在丰水年存储富余水量,平水年存储洪峰流量,从而在枯水年进行利用,改善枯水年的缺水现状。
4.3 R(t)的预测
根据前文介绍的方法,计算地表径流过程中剔除T(t)和P(t)后的序列,对得到的序列应用ARMA模型进行估计得到径流R(t)的模拟序列(表4)。由表4可知,阿克苏河、叶尔羌河、和田河和塔里木河干流的R(t)方程的显著性水平均小于0.05,回归方程显著。掌握R(t)变化趋势,可以确定洪峰和退水低谷期的水资源配置方案,在时间和空间上实现分段和分地区存储或补给水量,实现有限水资源的高效利用。
4.4 模拟精度评价
表5为ARMA模型和组合回归模型预测合格率和误差分析,图5为ARMA模型与组合回归模型预测结果对比。由表5和图5可见,组合回归模型的模拟效果良好,ARMA模型模拟效果很差。组合回归模型在率定期合格率为80.49%~90.24%,检验期合格率为63.64%~81.82%,可见精度均达到丙级以上,可用于参考性预报。经源流和干流对比发现,源流区组合回归模型模拟效果相对较好,基于组合回归模型,在确定不同利用方式的水流预测方程的情况下,可以基于实时预报的水文年特征,从时间和空间角度出发,建立研究区生态水流适应性利用方案。在丰水年,将生态变化随机性水量一部分用于补给生态用水量,一部分进行存储;在平水年,将洪峰期的生态变化随机性水量用于存储和补给生态用水量;在枯水年,利用前期存储的水量进行补给。根据生态天然补给量的变化趋势进行不定期分段水量补给,根据生态变化周期性水量进行定期分段水量补给,根据不同水平年的配置原则对生态变化随机性水量进行定期和不定期的分段水量分配。塔里木河流域水资源开发利用程度较高,致使周边生态环境严重恶化,结合生态水流情势制定的水量调度方案可以保障塔里木河生态系统的健康发展。

表4 R(t)方程及统计检验结果
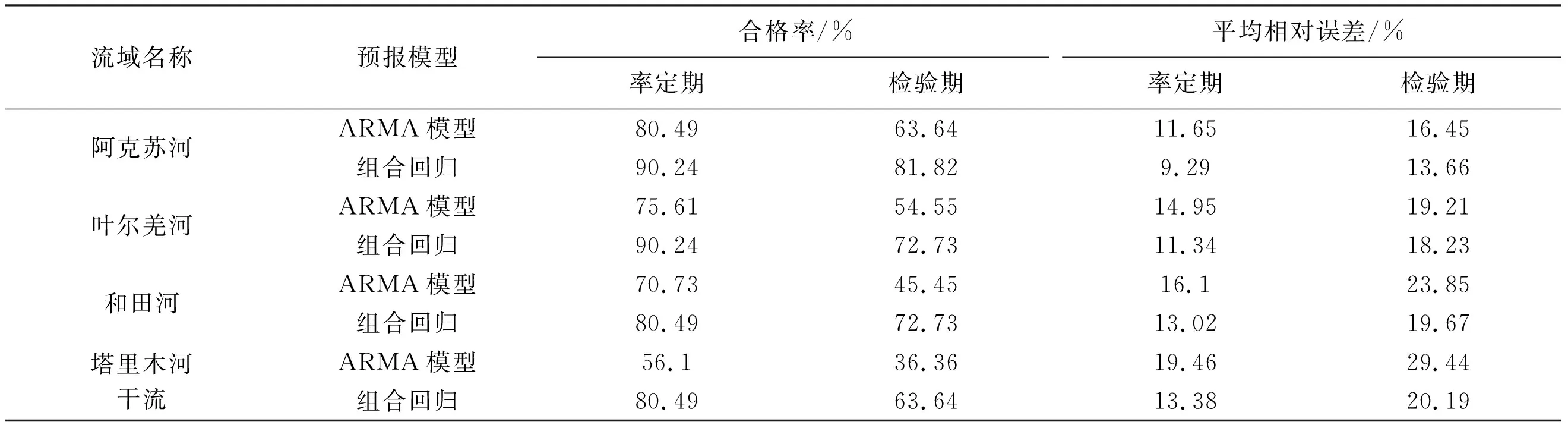
表5 ARMA模型与组合回归模型预测合格率及误差分析
注:ARMA模型的模型阶数为(1,1)。
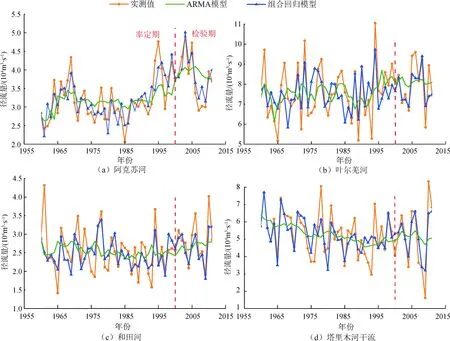
图5 ARMA模型与组合回归模型预测结果对比尤其是在阿克苏河流域,干流区预报相对误差较大,达到了20.19%,这是由于20世纪70年代以来,为满足农业发展需求,干流区生态水闸引水和水库调节灌溉的发展改变了天然的生态水流过程,错综复杂的人类活动干扰进一步增加了干流生态水文过程的随机性,致使干流生态水流序列趋近非平稳序列,模拟难度较大。
5 结 论
a. 源流区与干流区生态水流变化趋势不一致,呈现源流区径流增加、干流区径流减少的情势。20世纪70年代以来,源流区间耗水量呈现增长趋势,当源流来水频率小于50%时,源流区间耗水量的增加幅度较为明显,当频率大于50%时,区间耗水量减小幅度较为平缓。
b. 相对于ARMA模型,组合回归模型模拟效果比较理想,率定期、检验期的合格率分别为80.49%~90.24%和63.64%~81.82%,可作为参考性预报。根据研究区生态水流情势分析,建立不同水平年的生态水流适应性利用方案,在丰水年,将生态变化随机性水量一部分用于补给生态用水量,一部分进行存储;在平水年,将洪峰期的生态变化随机性水量用于存储和补给生态用水量;在枯水年,利用前期存储的水量进行补给。根据生态天然补给量的变化趋势进行不定期分段水量补给,根据生态变化周期性水量进行定期分段水量补给,根据不同水平年的配置原则对生态变化随机性水量进行定期和不定期的分段水量分配。

