基于TOF和RSSI的融合测距算法实现

李 波，马 恒，王彦本

(西安邮电大学通信与信息工程学院，陕西西安710121)

随着物联网和人工智能的快速发展，无线传感器网络正在逐步改变人与物、物与物之间的交互方式。对于大多数应用场景，获取节点自身位置信息是无线传感器网络应用的基础和前提。而获得节点的距离信息及距离信息的准确度直接影响位置信息的准确度。

无线测距的方法，主要有基于接收信号的接收信号强度指示(received signal strength indicator，RSSI)法［1-3］，该方法测距功耗低、成本低、实用性高，但是在远距离测距中误差大;基于信号达到时间的信号到达时间(time of arrival，TOA)法［4-5］和信号到达时间差(time difference of arrival，TDOA)法［6-7］，使用这两类方法测距需要节点间精确的时间同步，实现的复杂度高;基于信号到达角度的信号到达角度(arrival of angle，AOA)法，但AOA测距需要高精度的天线阵列，成本高［8］;基于飞行时间的飞行时间(time of flight，TOF)法，但TOF方法由于时钟偏移量的影响，在近距离测距中测距误差较大，适用于较远距离测距［9-10］等。这些单一的测距手段在多变的传感器网络中已不在适用，测距技术的融合应用是无线测距技术发展的趋势［11-12］。

基于RSSI测距在近距离段和TOF测距在远距离段有良好的测距性能。为了满足在不同距离段对测距的需求，且保证测距的精度和稳定性，本文拟在TOF测距技术和RSSI测距技术的基础上，提出并实现一种基于TOF和RSSI的多融合测距算法。该算法首先进行TOF测距和RSSI测距，得到多个初始测距值;其次，将初始值经过高斯模型得到测距最优值;最后，在不同距离段中，选择不同的加权因子，将TOF测距最优值和RSSI测距最优值进行融合，得到最优距离的估计值。

1 算法设计

在TOF测距技术和RSSI测距技术的基础上，本文算法将TOF远距离测距精度高和RSSI近距离测距精度高的优点相融合，以期实现一种更高精度的测距手段。算法原理，如图1所示。

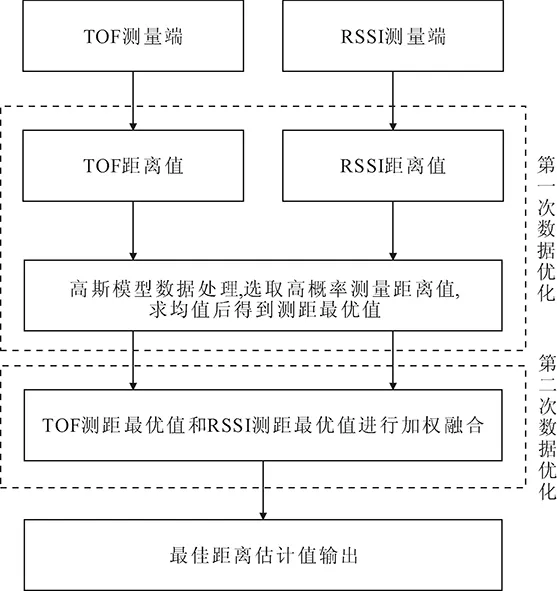
图1 融合测距算法原理

步骤1 应用TOF测距技术、RSSI测距技术得到测距初始距离值;

步骤2 应用高斯模型对初始距离值做预处理，得到测距最优值;

步骤3 应用加权模型在不同距离段中对测距最优值做不同加权因子的融合，得到最佳距离估计值。

1.1 基于TOF和RSSI的初始距离测量

RSSI距离测量采用的理论模型为渐变模型(shadowing model)［10］，在与发射端距离为 d 处的接收端得到的接受信号功率

其中，d0为基站与参考节点之间的距离;pr(d0)是参考节点在距离d0处的接受信号功率;X是一个平均值为0的高斯随机变量，其反映当距离一定时，接受信号功率的变化;n为路径损耗指数。

在实际应用中，采用简化的公式［10］

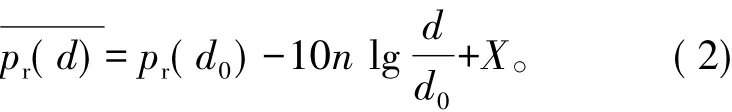
取d为1 m，从而得到实际应用中的RSSI测距公式测量的RSSI的值

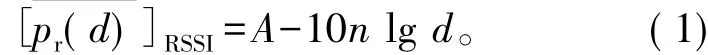
其中，A为信号传输1 m时接受信号的功率。

TOF距离测量过程中，发射端发送数据包到接收端，接受端收到后返还确认信息回应该数据包，其过程中飞行时间［10］

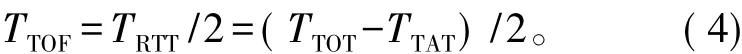
其中，TRTT为数据包实际飞行的往返时间，TTOT为发射端的总消耗时间，TTAT接收端用于接收数据和返还数据消耗的时间。

则发射端与接收端之间的距离

其中，c代表光速，取值为3×108m/s。

为了有效控制人为因素和环境因素对初始距离测量产生的影响，初始距离值的测量时选用空旷环境。信标节点端和未知节点端均固定在1.5 m的高度，在测量过程中，信标节点端始终固定，未知节点端移动。根据硬件实现，在每次移动2 m后分别记录保存20次TOF和RSSI的初始距离数据。在未知节点移动后，等待节点静止，然后采集下一次数据，测量值的选取应该具有广泛性。

1.2 基于高斯模型的最优值求解

在测距过程中，由于多变的环境、噪声的差异和测量误差等因素，导致直接测量得出的距离值中存在由于小概率事件引起的较大误差值。为了降低这种误差值对系统的影响，目前普遍采用多次测量后的统计平均值作为距离最优值。这种方法虽然在一定程度上减小了误差，但是，较大误差值依旧会严重影响测距精度。高斯模型的实现是选取系统中发生在高概率区的测量值，然后再取其统计平均值。这样可以避免测距过程中一些因小概率事件导致的较大误差值参与最优值的计算，从而提高系统的测距精度。

将测距过程中同一位置不同时间的测量值存储下来，利用高斯分布函数对测量值进行处理，得到随机测量值x的高斯分布函数

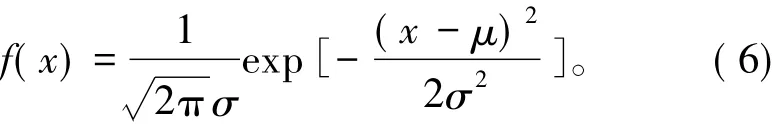
其中，σ为标准差，x为未知参数，μ为数学期望值，σ2为方差。

测量数据的均值m和方差σ2分别为

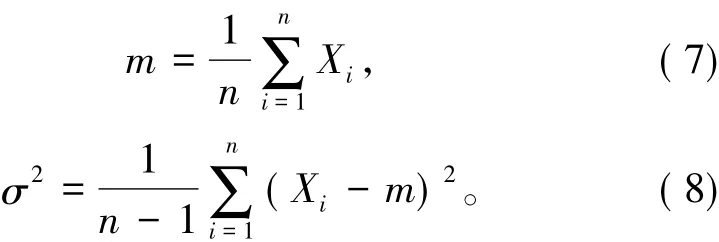
其中，Xi为第 i个初始测量值，i=1，2，…，n，n 为测试总个数。

确定可选值范围，高斯分布函数的临界值

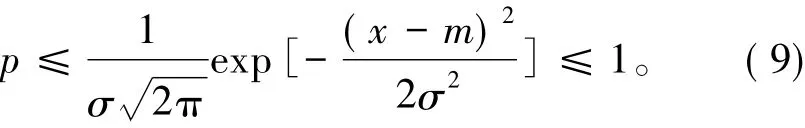
根据多次实验的经验，选择p的值为0.65。当高斯分布函数的值大于0.65时认为测量值为高概率发生值;当高斯分布函数的值小于0.65时认为测量值为小概率误差值。

从测距初始值中选取满足要求的值Di，满足高斯模型值的个数为z。得到测距最优值

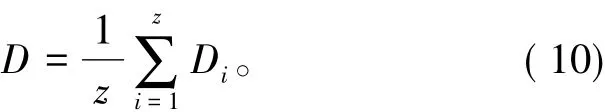
其中，Di为第i个满足要求的值，i=1，2，…，z，z为满足要求的个数。

高斯模型解决了在测距过程中由于小概率事件导致的误差值对整体测距精度的影响，提高了系统的测距精度和稳定性。

1.3 最优值的加权融合

单一的测距手段只能满足规定情景下的测距，为了保证多种环境下测距的有效性，将RSSI近距离测距精度高和TOF远距离测距精度高的优点相融合，形成不同距离段中不同加权因子的RSSI和TOF动态融合测距方法，得到最佳距离估计值

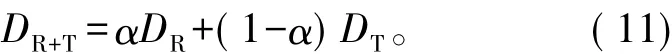
其中，DR为RSSI测距得到的最优值，DT为TOF测距得到的最优值，α为加权因子，α在不同的距离段取值有差异。

加权模型用TOF远距离测距精度高的优点弥补了RSSI远距离测距信号强度不稳定的缺点;用RSSI近距离测距精度高的优点弥补了TOF近距离测距易受时钟偏移量影响的缺点。在中间距离段，两种方法的测距精度相当，但是为了提高了测距的稳定性，采用动态加权因子将RSSI测距和TOF测距相融合。

2 系统实现

研究平台基于SEMTECH公司的LoRa 2.4 G射频集成模块，该射频模块可以提供2.4 G的扩频通信调制，是一款高性能无线收发器。其内部集成了TOF测距引擎，同时其数据帧中提供了RSSI参数。

2.1 硬件实现

系统硬件由TI公司生产的MSP430F4152微控制器作为主处理器、SEMTECH公司生产的LoRa 2.4 G模块作为无线收发器，以及其他外围控制电路组成。

系统控制器的主要功能是无线收发器的初始化和控制，以及数据的存储和计算。系统控制器与无线收发器之间的传输接口为全双工的高速串行外设接口(serial peripheral interface，SPI)。

无线收发器负责数据的收发。控制器可以通过SPI总线对无线收发器的扩频因子(spreading factor，SF)、带宽(band width，BW)、编码率(coding rate，CR)进行配置。在不同的环境中选用适用环境的配置，可以更优的获取测距信息。

2.2 软件实现

系统软件部分由信标节点端和未知节点端组成，不同端的软件算法流程，如图2所示。

从图2可以看出，信标节点端软件运行流程分为3个阶段:首先发送普通数据包用以搭建无线通信链路;其次进行测距数据包传输，得到多个测距初始值;最后对测距初始值进行算法优化，计算出最佳测距估计值。

未知节点端软件运行流程分为2个阶段:首先等待信标节点发送普通数据包，进行地址校验后回复确认字符(acknowledgement，ACK)数据包表示无线通信链路搭建完成;然后在收到测距数据包后，回复测距相关信息，输出最佳测距估计值。

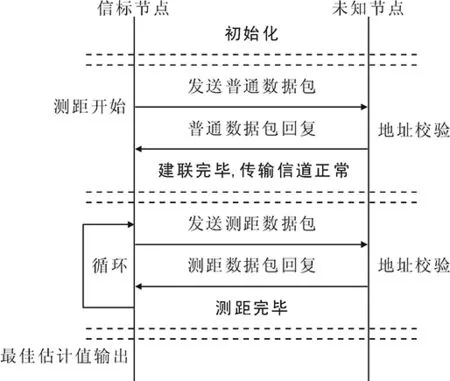
图2 软件算法流程

3 实验结果及分析

在空旷的环境下，使用基于LoRa 2.4 G搭建的测距系统对所述融合算法进行有效性验证。

基于RSSI方法的测距结果，如图3所示。由图3可知，较于传统的直接采用均值模型测距，基于高斯模型的测距误差更加稳定、测距精度更高。在近距离测距中，RSSI测距有误差小、测距精度高的优点。尤其体现在0～10 m的距离段，测距误差在1 m以内。

基于TOF方法的测距结果，如图4所示。从图4中可以看出，基于高斯模型的测距在误差和精度方面较基于均值模型的性能更优，其抑制了小概率事件引起的误差对整体系统的影响。在远距离测距中，TOF测距的误差小、测距精度高。尤其体现在25～50 m的距离段，测距误差在2 m以内。

基于TOF、RSSI和本文所提融合算法的测距结果，如图5所示。从图5可以看出，不同测距手段的优势体现在不同的距离段，采用本文提出的融合算法可以将RSSI测距和TOF测距的优势相结合。该融合算法在0～10 m的距离段，针对RSSI近距离测距精度高的优点，取α的值为1;在25～50 m的距离段，针对TOF远距离测距误差小的优点，取α的值为0。在10～25 m的距离段，两种测距方法测距精度相当，但稳定性较差，为此将两种测距方法融合，依据实验测试得出的经验值，在10～17 m的距离段内，取α的值为0.536，在17～25 m的距离段内，取α的值为0.303。从图5中可以看出，在近距离段和远距离段中应用RSSI和TOF融合算法时，测距精度优于采用单一算法的测距精度;在中间距离段中应用RSSI和TOF融合算法时，测距稳定性有了提升。

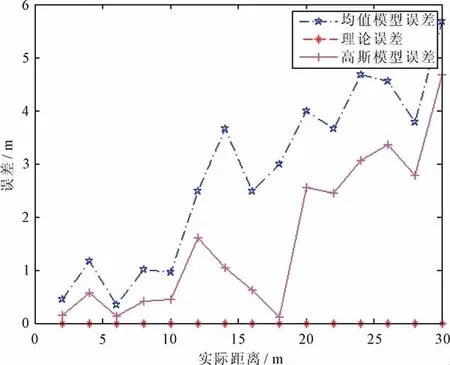
图3 基于RSSI方法测距结果

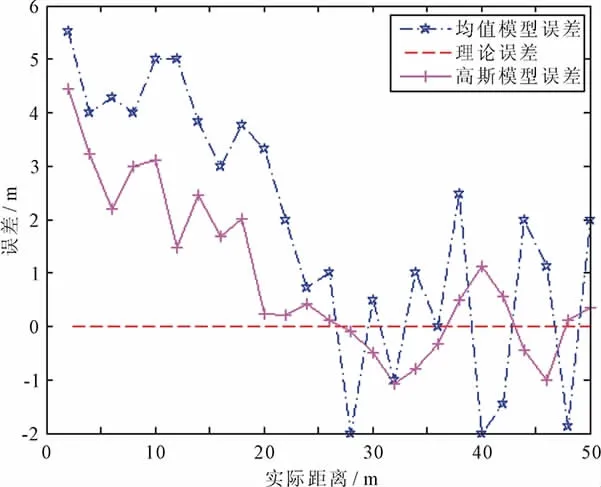
图4 基于TOF方法的测距结果

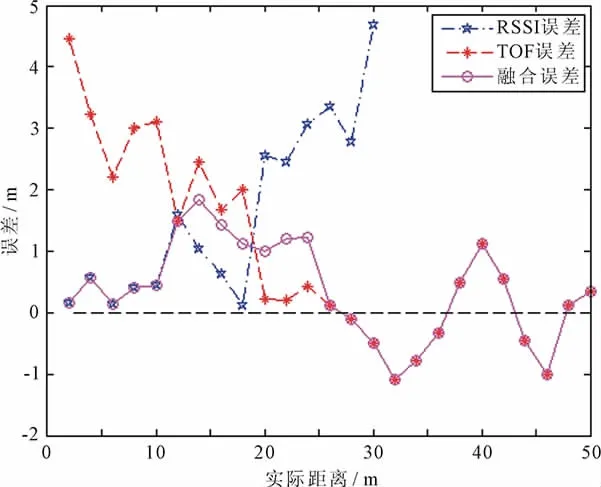
图5 不同算法的测距结果

4 结语

为了提高无线测距的精度和稳定性，在RSSI测距和TOF测距的基础上，提出了一种基于TOF和RSSI的多融合测距算法。该算法首先使用了高斯模型方法，将测距初始值中由小概率事件影响的测距误差值剔除，降低了初始值的不稳定性对系统的影响;然后基于加权模型融合了RSSI测距和TOF测距，在不同的距离段中选用不同的加权因子，使得整体系统在测距中都有良好的精度和稳定性。对比于其他单一算法，本文所提的融合算法既减小了测距过程中误差对整体系统的影响，提高了测距的精度;也弥补了采用单一测量方法时无法满足不同距离段的劣势，提高了测距的稳定性。