显著信息引导的直觉空间模糊聚类图像分割

赵 凤，郝 浩

(1.西安邮电大学通信与信息工程学院，陕西西安710121;2.电子信息现场勘验应用技术公安部重点实验室，陕西西安710121;3.陕西省无线通信与信息处理技术国际合作研究中心，陕西西安710121)

图像分割指的是根据像素的灰度、颜色、纹理、形状等一些特征信息，将图像划分成一些具有特殊性质的区域，这些区域的交集为空集，并集是整幅图像，并且这些特征在不同区域之间表现出明显的差异性，在同一区域内表现出较高的相似性［1］。目前，具有代表性的图像分割算法主要有基于边缘检测的分割法［2］、基于阈值的分割法［3］、基于区域的分割法［4］和基于聚类的分割法［5-8］等。

模糊C-均值(FCM)算法是一种基于目标函数的聚类分析法，优化目标函数后得到每个待分类对象对所有聚类中心的隶属度，然后决定每个对象的归属，完成自动分类［9］。把空间信息邻域限制项引入到FCM算法，可得改进的聚类算法(FCM_S)［10］，对其加以改进，还可得到引入了邻域均值空间信息的FCM_S1算法和引用了邻域中值空间信息的FCM_S2算法［11］。广义模糊 C-均值(FGFCM)聚类算法［12］对于图像噪声具有较好的鲁棒性。模糊局部信息C-均值(FLICM)聚类算法［13］定义了新的模糊因子，考虑了邻域像素的局部空间信息和灰度信息，故对图像噪声具有更高鲁棒性。相比于模糊集，直觉模糊集(IFSs)［14］能够更准确的展示事物的模糊性，更能描述客观世界的模糊本质［15］。将FCM算法在直觉模糊集下推广，可以得出直觉模糊C-均值(IFCM)聚类算法。

IFCM算法没有引入任何空间信息，应用于图像分割时受噪声的影响很大，并且IFCM算法对聚类中心的初始值很敏感，不合适的初始值很容易导致算法陷入局部最优解。为了改善上述情况，本文将给出一种应用于图像分割，由图像的显著性信息引导的包含空间信息的直觉模糊聚类分割算法。该算法使用图像的显著信息和灰度直方图统计信息来初始化聚类中心，并且把改进的局部空间信息引入到传统的直觉模糊C-均值聚类算法中，提高算法对于噪声的鲁棒性。所给改进算法不易陷入局部最优解，对不同类型的噪声具有较强的鲁棒性。

1 直觉模糊集

模糊集只考虑了隶属度特征，而改进后的直觉模糊集既考虑了隶属度特征，又考虑了非隶属度和犹豫度等特征信息。设有限的论域X={x1，x2，…，xn}上的直觉模糊集A表示为

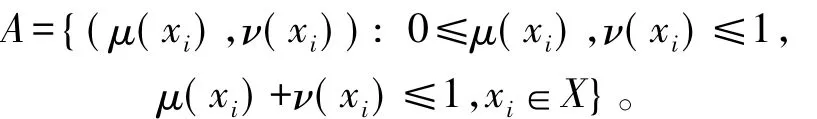
其中，μ(xi):X→［0，1］和 ν(xi):X→［0，1］分别表示在直觉模糊集下，样本点xi对应的隶属度函数和非隶属度函数。当μ(xi)=1－ν(xi)时，直觉模糊集成为普通的模糊集。

在非隶属度的基础上，为了更好的反应数据的不确定性，引入变量犹豫度［14］

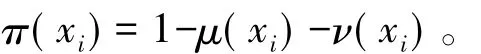
为了构造非隶属度函数ν(xi)，利用例如Yager算子［16］等很多基于隶属度函数，即可产生非隶属度的算子。

2 显著信息引导的直觉模糊聚类

2.1 基于显著性区域的聚类中心初始化

图像的显著性区域就是图像中令人感兴趣的区域［17］。图像中各个类别的内部区域集中大量灰度值接近的像素点，这些像素点的频数形成的直方图曲线会呈现出峰值，所以，一幅直方图可以客观体现一幅图像的类数特征，对灰度直方图进行分析可以确定初始化的聚类中心［18］。使用显著性目标的检测算法［19］可确定显著性图像，公式为

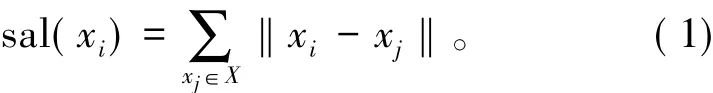
其中，xi表示图像像素集和X中像素i的灰度值，每一个像素的显著性数值指的是，这个像素与图像中其他像素某种距离的数值和，这种距离一般使用欧式距离［19］。

#3096实验图通过公式(1)得到的显著性图如图1所示。使用分水岭阈值分割算法［20］把显著性图分为显著性(白色高亮)的区域和非显著性的区域两部分。在显著性的区域，统计其对应的灰度值，选择频数最大的灰度级作为第1个初始聚类中心;在非显著性的区域，统计对应的灰度值，选择频数最大的前K－1个灰度级，作为第K－1个聚类中心。因此，可以从显著性的区域和非显著性的区域共选出了K个聚类中心。

图1 提取显著性区域

2.2 融合局部空间信息的直觉模糊聚类

为提高改进算法对于图像噪声的鲁棒性，减少噪声对图像分割带来的影响，设计一种新的融合局部空间信息的模糊因子，添加到IFCM算法中，给出融合局部空间信息的IFCM算法，其目标函数为

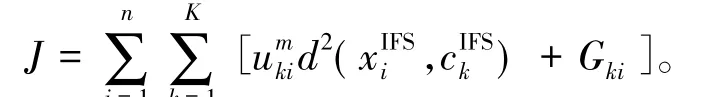
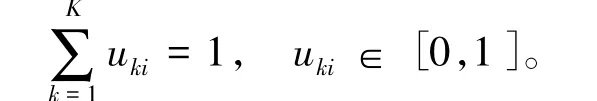
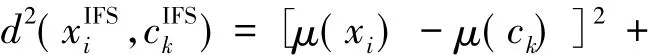
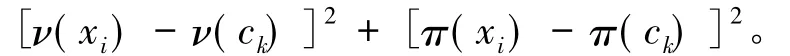
μ(xi)是像素xi对于图像集合的隶属度，定义为

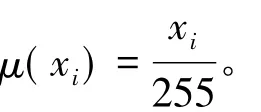
ν(xi)是用Yager算子［16］求得的非隶属度，表示为

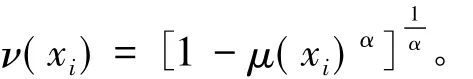
α 是参数，取［16］α =0.85。犹豫度 π(xi) 定义为

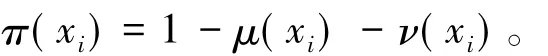
Gki是模糊因子，定义为

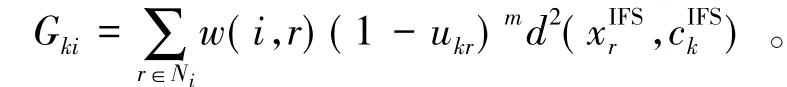
w(i，r)表示像素i与其邻域窗内的像素点r之间的相关程度，w(i，r)考虑了像素的灰度信息和空间位置信息，表示为

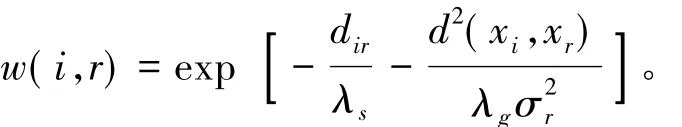
dir表示像素点i和像素点r的位置信息，表示为

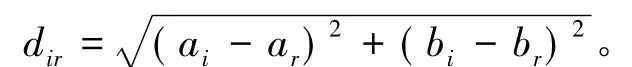
(ai，bi) 和(ar，br) 分别是表示像素点 i，r的空间坐标。d2(xi，xr)表示像素 i，r的灰度信息的欧氏距离。λs和λg是尺度参数，一般均取3［12］。σr定义为

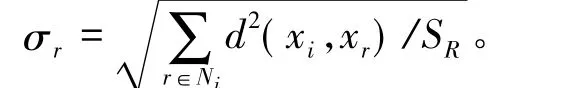
其中，Ni表示以像素点i为中心的邻域窗口，SR为邻域窗口内像素的个数。

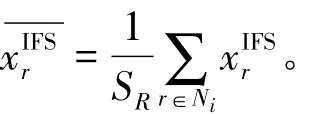
其中，SR为邻域窗口内像素的个数。

利用拉格朗日乘子法可求得隶属度函数uki与聚类中心，分别为

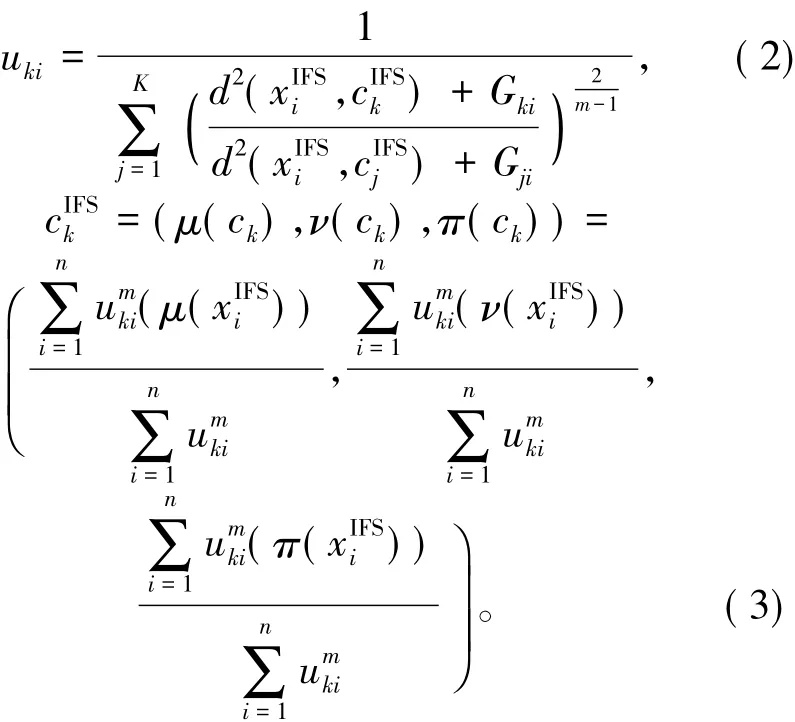
2.3 算法流程

算法的具体步骤可描述如下。

输入 图像像素集 X={x1，x2，…，xn}，聚类个数 K(2＜K＜n)，最大迭代次数 T，停止阈值 ε=10－5，模糊加权指数m，邻域窗大小ω，参数λs和λg。

输出 图像分割结果。

步骤1 根据公式(1)求得图像的显著性图。

步骤2 根据分水岭算法，把显著性图像分成显著性的区域和非显著性的区域。统计显著性的区域的灰度值第1个初始聚类中心，统计非显著的性区域的灰度值分别得到第(K－1)个初始聚类中心。

步骤3 根据公式(2)更新隶属度。

步骤4 根据公式(3)更新聚类中心。

3 实验结果与分析

为了验证所给改进算法的有效性，采用FCM、FCM_S1、FCM_S2、FGFCM、FLICM、IFCM 等 6 种算法作为比较算法，1幅人工合成图像、4幅Berkeley图像［21］、4 幅刑侦图像［22］作为实验图像。算法参数设置为［6，12］:隶属度模糊参数 m=2;邻域窗口大小ω =3;参数λs=3，λg=3;停机准则条件ε =10－5;最大迭代次数T=200。为了评价算法的有效性，使用分割准确度(segmentation accuracy)［23］

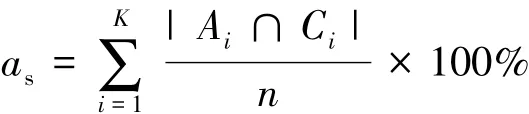
作为算法分割效果的指标。其中K表示聚类中心的个数，︱·︱表示正确分类的像素点集合，Ai表示经过算法处理后属于第i类的像素点集合，Ci表示标准分割图中属于第i类的像素点的集合。as表示正确分类的像素点个数占图像像素点总个数的比重。

3.1 合成图像分割实验

图2是人工合成实验图，各个比较方法在人工合成实验图上的分割准确率展示在表1中。其中:高斯噪声图的高斯噪声均值为0，方差为0.01;椒盐噪声图的椒盐噪声系数为0.05。此外，图3和图4中展示了算法分割结果。从分割准确率数据和分割效果可见，所给改进算法的效果优于其他参与对比的6种算法。

图2 人工合成实验图

图3 含高斯噪声的人工合成图分割效果

图4 含椒盐噪声的人工合成图分割效果

表1 7种算法对含噪声人工合成图像的分割准确率/%

3.2 Berkeley图像分割实验

考察所给改进算法的性能。选择4个Berkeley图像进行分割实验。表2展示了4个图像在不同噪声类型、不同噪声强度水平下各方法的分割数据准确率结果。从表2的分割准确率数据中可以看出，所给改进算法对于不同图像的分割准确率最好。

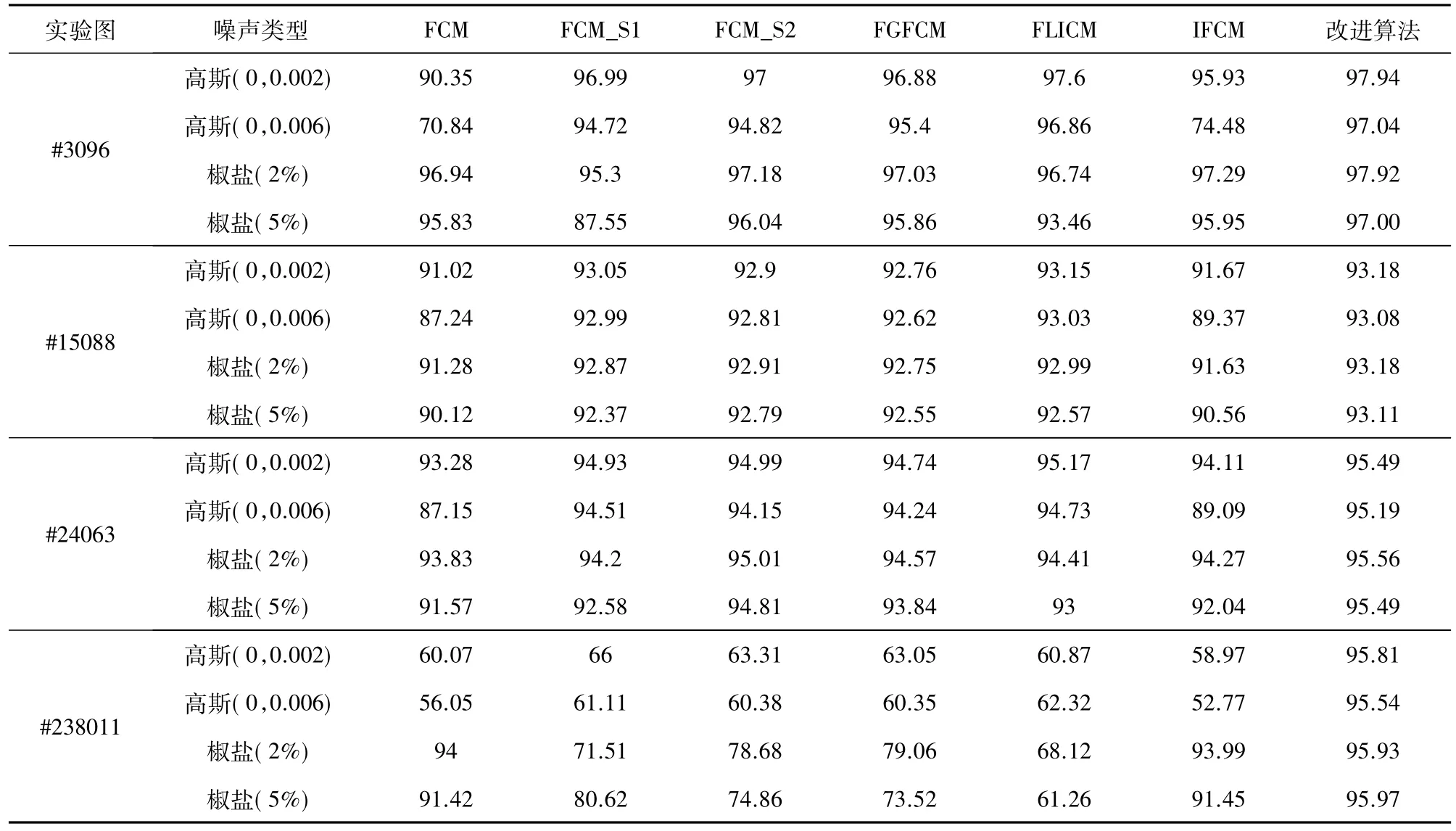
表2 7种算法对含噪声Berkeley图像的分割准确度/%

选取#3096和#238011的分割结果进行展示。图5展示了#3096和#238011的噪声图和标准分割图，其对应的分割效果如图6至图9所示。对于图像#238011，6种对比算法很难准确的把图中的月亮分割出来，而所给文算法因为采用显著性信息引导初始化聚类中心的方法，能够获得理想的分割结果。综上考虑，所给改进算法在4幅图像上能够获得优良的分割结果。

图5 噪声图及标准分割图

图6 含高斯噪声的#3096图分割效果

图7 含椒盐噪声的#3096图分割效果

图8 含高斯噪声的#238011图分割效果

图9 含椒盐噪声的#238011图分割效果

3.3 刑侦图像分割实验

为了考察所给改进算法在刑侦图像上的分割性能，选取刀具、指纹、轮胎印和足迹等4幅刑侦图像进行测试。

刑侦图像如图10所示，刑侦图像分割结果如图11至图14所示。分析分割图像，所给改进算法对噪声的鲁棒性要强于其他对比方法，并且能够保留图像的细节信息。

图10 刑侦图

图11 含高斯噪声的刀具刑侦图分割效果

图12 含高斯噪声的轮胎印刑侦图分割效果

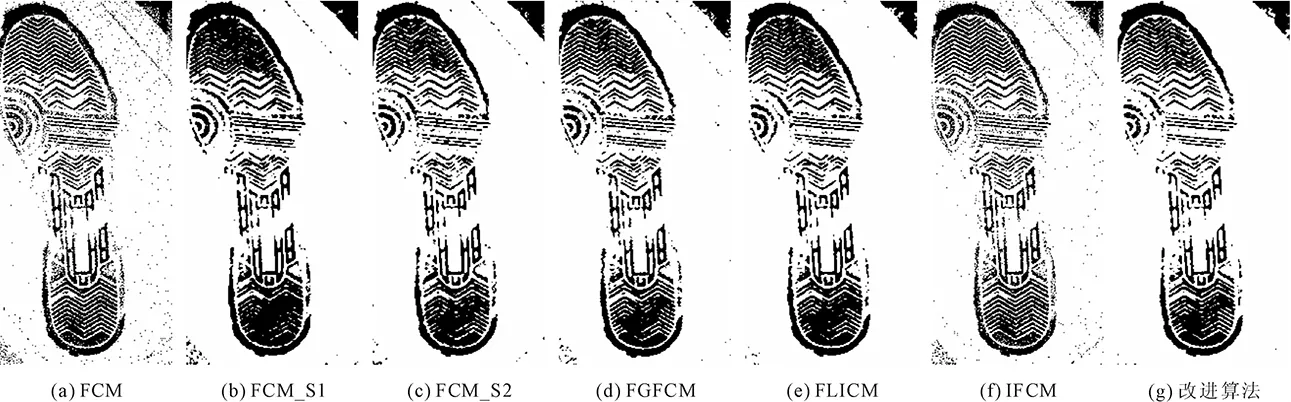
图13 含高斯噪声的足迹刑侦图分割效果

图14 含椒盐噪声的指纹刑侦图分割效果

4 结语

给出了显著信息引导的直觉空间模糊聚类图像分割算法，利用图像显著信息来初始化聚类中心，将改进的融合局部空间信息的模糊因子，引入到传统直觉模糊C-均值聚类算法。经过大量的仿真实验表明，所给改进算法对图像噪声不敏感，并且能够很大程度避免算法陷入局部最优解，能得到较好的分割效果图。