Divisive hierarchical clustering on cuboids for fast image/video coding and analysis

MURSHED Manzur

(Faculty of Science and Technology，Federation University Australia，Churchill Vic 3842，Australia)

Abstract:Region-based image retrieval(RBIR)has been proven to be effective in finding relevant images.It will form the basis for intelligent video surveillance where features of regions-of-interest(ROI)is extracted in real-time.This paper presents a review on existing image segmentation techniques based on the classical clustering approaches，including a novel Cuboid Segmentation(CSeg)technique that results in approximated rectangular image segments.CSeg is fast with minimum possible linear order running time and performance of RBIR using the approximated segments is statistically similar to RBIR using accurate segments from segmentation techniques that are infeasible for real-time applications.

Keywords:hierarchical clustering，cuboid segmentation，image/video analysis，image/video compression

Clustering，aka cluster analysis，is one of the fundamental tools in data science with ubiquitous applications in many fields，including machine learning，data mining，information retrieval，image analysis，and data compression to name a few.Nevertheless， the notion of “cluster” has no universal definition when it is used in various fields.A widely accepted generic definition of clustering is a process of splitting a dataset D into a set of“meaningful”subsets of data D1，…，DkD(k∈+)， that are termed as clusters.Meaningful clustering，however，is in the eye of beholder［1］.Often it is quantitatively expressed with some similarity metric that transforms clustering into an optimization problem with the multi-objective function maximising the intra-cluster similarity while concomitantly minimizing inter-cluster similarity.

The simplest form of similarity metric is defined with a distance function d(p，q)between two data points p and q.Extending this to define a distance function D(Di，Dj)，between two clusters Diand Dj(1≤i，j＜ k)，however，is not quite straightforward.There are|Di|×|Dj|distinct pairs of points〈pi，qj〉where pi∈ Diand qj∈ Dj.Often some measures of central tendency，such as mean，median，and mode，or extrema，such as minimum and minimum，on the distances of all distinct pairs of points.For the arithmetic mean measure of central tendency，D(Di，Dj)may be defined as

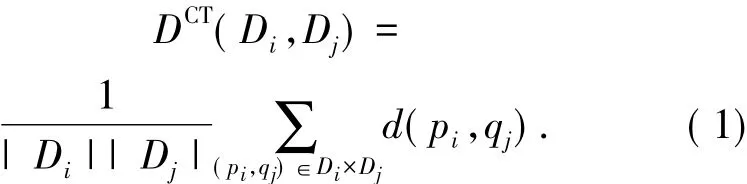
For extrema measures，D(Di，Dj)may be defined as

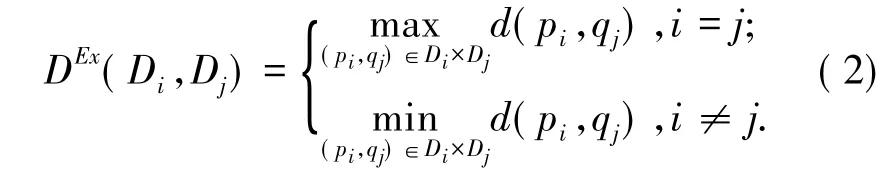
The multi-objective function of the clustering optimisation problem may then be expressed as

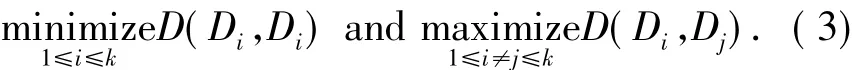
This optimization problem， however， is NP-Hard for which a polynomial-time algorithm is not known.Thus the common approach is to search only for approximate solutions with heuristics for different cluster models focusing on centroids，distribution，density，and connectivity(e.g.，graphs and trees).

In this review paper， existing image segmentation techniques are briefly presented，including a novel segmentation technique on cuboids，which is fast enough to be implemented in real-time applications.

1 Clustering for image/video analysis

Clustering is widely used in image/video analysis in the form of image/video segmentation and background/foreground separation with applications in content-based indexing and retrieval(CBIR)，image/video annotation，object detection and recognition，machine vision，medical imaging，and video surveillance.Let n=|D|be the number of pixels under consideration. Clustering for image/video analysis labels each pixel p with the index of its cluster i(p)=i iff p ∈ Di.Almost all classical clustering approaches have been attempted for image/video analysis.In the following subsections， some of the key attempts are highlighted.

In the classical cluster analysis e.g.，in data mining，location of the data points play a secondary(if any) role in defining the distance function，which primarily considers the attributes of data points.Cluster analysis in image/video analysis，however，has to consider the spatiotemporal location among the primary attributes of data points(pixels)as neighbourhood proximity of pixels is a prerequisite for meaningful clustering.Intuitively speaking，it is desirable to assign the same segment label to spatially adjacent pixels.

Let I(p)∈δand α(p) ∈［0，1］3denote the location and attribute of pixel p，respectively.The location is represented by the 2D(δ=2)or 3D(δ=3) coordinate of p in an image or a video，respectively.The attribute is represented by a 3D vector denoting a colour value in a 3D colour model e.g.，RGB，HSV，HCL，and YCbCr.For many clustering approaches，it is not a natural option to analyse the similarity of the colours and their spatial distributions at the same time［2］.An alternative is to decouple spatial distribution of pixels from their colour similarity，leading to a post-processing stage on spatial segments after performing initial clustering on colour attributes only.Let dI(p，q)and dα(p，q)denote the distance function between two data points p and q using their locations I(p)and I(q)，and attributesα(p)and α(q)，respectively.

(A)Centroid-based clustering

The main centroid-based technique is k-means clustering［3-4］where each of targeted k clusters Di，1 ≤ i≤ k， is represented by the centroidof its member pixels in the attribute domain.For an initial set of k random centroids，each pixel p∈D is assigned to its nearest segment，i.e.，i(p)=argmin1≤i≤kd(p，ci) and ci’s are recomputed iteratively until converged when the assignments no longer change.Running time of k-means clustering is O(kδτn)， where τ is the number of iterations needed until convergence.For segmenting image/video，where the attributes are quantised， τ = O(n3)， leading to the overall complexity of O(kδn4)=O(n4).

The post-processing stage for considering spatial distribution can be performed in many ways.Of these，J-value based spatial segmentation used by the popular JSEG algorithm［2］is prominent.For any image segmentation outcome with k segments，J=is a measure of cluster homogeneity whereσ2andare the variance of pixel location from the centroid for the whole image and the i th segment，respectively.The higher the J-value the stronger the homogeneity in segments.

Fuzzy c-Means clustering［5］is a soft version of k-means(k=c)，where each data point p is labelled with a weight vector i(p)=(wp，1，…，wp，c)depicting the fuzzy degree of belonging to each cluster.

(B)Density-based clustering

Density-based clustering such as DBSCAN(Density Based Spatial Clustering of Applications with Noise)［6］is directly focused on the spatial distribution of data points and thus can be readily used for image/video segmentation［7-8］.It first divides each pixel p∈ D into low-density(noise)or high-density(cluster members)classes by inspecting whether the number of similar(dα(p，q) ≤ thα)pixels in its spatial-neighbourhood(Np={q|dI(p，q) ≤ thI})is less than thminor not，respectively， where thI， thα， and thminare user-defined parameters.A cluster D1is then formed from a high-density pixel seed p by including all similar pixels in Np，irrespective of their density，and then iteratively perform the same on all newly added high-density pixels.This process is iteratively applied for a new high-density pixel seed that has not been processed yet to discovery more clusters D2，…(if any).

DBSCAN does not require users to specify the number of clusters in the dataset a priori.However，it cannot cluster datasets well with large differences in densities，since the parameters cannot be adapted appropriately for all clusters.Running time of DBSCAN is O(δn|Np|).For image/video segmentation，a fixed spatial-neighbourhood window N of size|N|=O(1)pixels is considered，leading to the overall complexity of O(|N|δn)=O(n)，the minimum possible bound.

(C)Distr ibution-based clustering

Distribution-based techniques depart from the notion of estimating similarity of the data points in a cluster from their pair-wise distances defined in(1)and (2).Instead each cluster is statistically modelled with a parametric probability density function(pdf)under the assumption that 3D colour vector of pixels in a natural image/video is analogous to samples drawn from a finite mixture distribution.Gaussian Mixture Model(GMM) is the most prominent where a cluster is modelled with Gaussian density f(p| θ)with model parameterθ=(μ，σ).

GMM has been used for segmentation of noisy images［9］where a mixture of L Gaussians with parameters θ1，…，θLrepresent L target segments.Membership of the i th pixel pi，1 ≤ i≤ n，is expressed with the vector πi=(πi，1，…，πi，L)where πi，j，0 ≤ πij≤ 1，denotes the probability of pibelonging to Dj，i.e.，GMM is then defined as

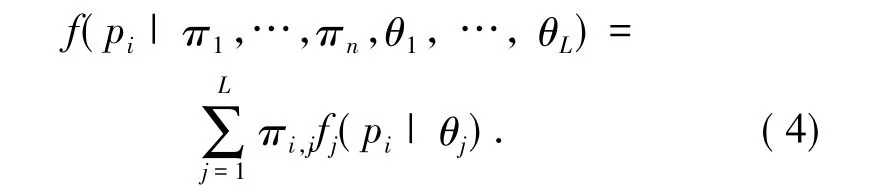
Assuming all pixels are statistically independent，maximum-likelihood estimator(MLE)of parameters π1，…，πnand θ1，…，θLcan be calculated using the iterative expectation-max-imization(EM)algorithm for any initial estimate of the parameters.Consideration of spatial distribution can be easily incorporated in the estimation process with a suitable prior density function.Running time of GMM-based clustering is O(Lτn)，where τ is the number of iterations needed until convergence.Convergence of EM，however，is very slow.The first few EM iterations climb up to a local maxima quickly，but later iterations moves very slowly.

(D)Hierarchical clustering

In hierarchical clustering based image/video segmentation，segments are represented with a tree data structure with D as the root node，pixels(or superpixels［8］)as the leaf nodes，and progressively constructed clusters as intermediate nodes.Approaches for hierarchical clustering are agglomerative(bottom-up)and divisive(top-down).

In agglomerative approach［10］，D is first divided into ns= n/c superpixels，perceptually meaningful grouping of on average c spatially neighbouring pixels，using an O(n)algorithm where c is a small constant.From an initial forest 珚D.of nstrees，each having a superpixel as root with no children，the closest two boundary-adjoined trees

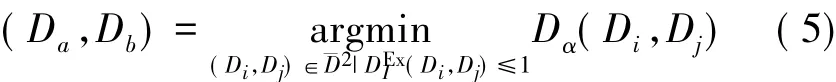
are iteratively replaced in珚D with their merged tree，having a new internal node as root with Daand Dbas two children，until only a single tree is left in珚D.Any cut of this tree results in a forest of subtrees，each representing a segment.Running time of this agglomerative hierarchical segmentation is O(n log ns).

In divisive approach［11］，D is recursively split with k-means clustering until satisfactorily high J-value is reached.The parameter k at each split is adaptively selected by iteratively clustering with k=2，…，kmaxuntil J-value is no longer increasing monotonically.Running time of this divisive hierarchical segmentation is O(kmaxδn4log n).

A hierarchical segmentation algorithm using both merging and splitting was proposed in［12］on quadtrees.Unlike other segmentation techniques that aim to produce accurate arbitrary-shaped segments，this algorithm produces segments with boundaries as polygons of only horizontal or vertical lines.

(E)Limitations

The existing segmentation techniques presented above suffer from one or more of the following limitations in their potential applications.1)They are semi-supervised in the sense that the initial solution caps the number of segments.2)They are very slow to converge.3)The iterations are highly serialized with little opportunity to speed-up with parallel processing.4) The outcome provides no spatiotemporal relations among the segments.5)Encoding the boundary of the arbitrary-shape segments is inefficient.

2 Divisive hierarchical clustering on cuboids

Image segmentation is an essential pre-processor for analysing the content efficiently.Global features extracted from unsegmented images exhibit strong central tendency and hence rarely carry any meaningful and distinctive information.The goal of segmentation is to split an image into regions that are sufficiently homogeneous to be represented with meaningful features and reasonably distinct from the adjacent regions.Features and segmentation are，therefore，interrelated.We expect the segmentation outcome to localise features in real-time using the feature-space specified for an application.Existing segmentation techniques are not suitable for this purpose due to high computational complexity and high bit-overhead of encoding the segments.Moreover，these segmentation approach cannot be adapted to specified feature-space with a single algorithm.

Recently，we developed a novel Cuboid Segmentation(CSeg)technique，which has been successfully used to i)design a near-lossless depth sequence coder［13］with compression efficiency superior to the lossy depth coder in the latest 3D-HEVC multiview video coding standard;ii)develop a lossless image coder［14］superior to the latest JPEG-LS standard;iii) design an efficient lossless coder［15］for hyperspectral images; and iv)improve performance of CIBR using colour moments features［16］.

CSeg offers single-algorithm solution，which can adapt to specified feature-space feature-space F，so long a distance metric DF(D1，D2) between sub-images D1and D2is well-defined.It uses a divisive hierarchical clustering heuristic to recursively split a rectangular image D of size X × Y=n into two rectangular halves Dh，1and Dh，2with an optimal split-hyperplane h*，orthogonal to one of the axes(Fig.1a)，such that the distance is maximized，i.e.，

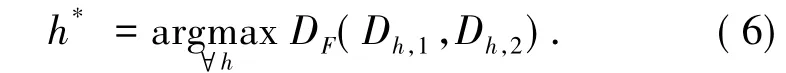
As there are X+Y －2 possible lines to split，h*can be signalled with log2(X+Y － 2)bits.The recursion is terminated when DF(Dh，1，Dh，2)is below a threshold or the target granularity (minimum cuboid size)is reached.It can be configured to partition at coarser granularity with large cuboids(Fig.1c)or finer granularity with small cuboids(Fig.1d). Nevertheless， CSeg preserves the perceptual quality of the segmentation at any granularity.Note that the key objects in the image，a car，two trees，and the sky，have been segmented out at both granularities(Fig.1c and Fig.1d) .The segment boundaries are collectively expressed with a binary partition tree (Fig.1b) of recursive optimal splits.

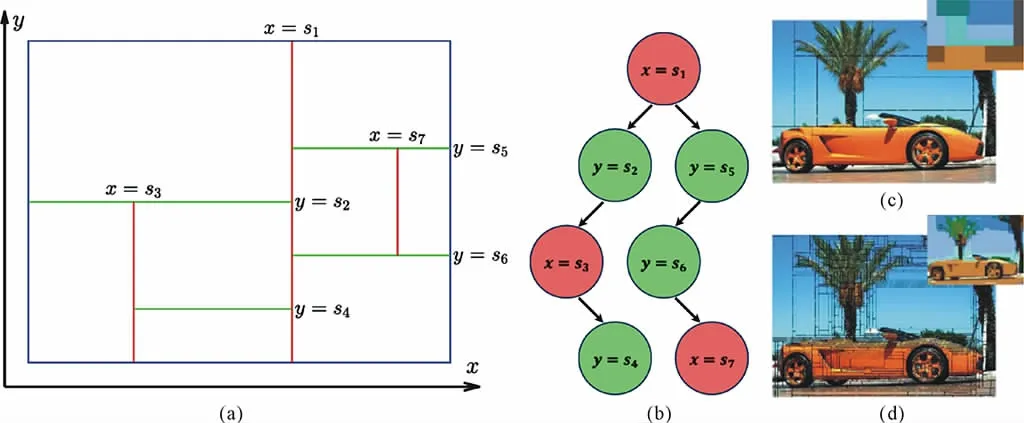
Fig.1 (a)Divisive hierarchical clustering heuristic in CSeg;(b)corresponding partitioning tree;and image segmentation with CSeg at(c)coarse and(d)fine granularity using colour moments feature-space(the segments are shown in the inset).

CSeg has successfully addressed the limitations of the existing segmentation techniques outlined in Section II.E.CSeg is free from the aforementioned limitations of the existing techniques.1) It is unsupervised in the sense that any possible number of segments at the target granularity can be obtained auto-matically.2)It is very fast.Not only the depth of recursion is bounded logarithmically but it can also take advantages of matrix processing and the specialized hardware e.g.，graphics processing unit(GPU).3)The divisive hierarchical approach is readily amenable to parallelism.4)The partitioning tree(Fig.1b) provides rich spatiotemporal cues.5)Encoding the boundary of cuboid segments is straightforward coding of the partitioning tree in the preorder traversal sequence.

The integral imaging approach［17］will be key to achieve this objective.This approach first computes an intermediate table of cumulative area-sum from the origin

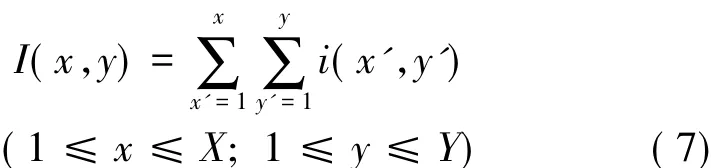
in O(n)time，which can then be used to compute the area-sum for any arbitrary rectangley')as I(x2，y2) － I(x2，y1) － I(x1，y2)+I(x1，yi)in constant O(1)time.

Let T(n)be the running time of CSeg using integral imaging.For simplicity，let us assume each optimal split divide D into proper halves，and X and Y are of O(槡n).The time to find the first optimal split is(X+Y－1)×O(1)=O(2槡n).We may then use the following recurrence relation

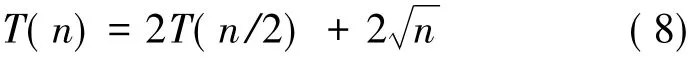
to conclude T(n)=O(n).Considering O(n)time for initialising the area-sum table，the overall running time of CSeg is O(n)，the minimum possible bound.

3 Performance of CSeg in CIBR

We compare performance of CSeg against JSEG in CIBR with image partitioning on the eBay dataset from ［18］ containing images collected from eBay auction site(www.ebay.com).The dataset has four object classes:cars，dresses，pot_glass，and shoes.Each class contains 12 images for each of the 11 colour classes，assigned by eBay users.There are a total of 4×11×12=528 images.

CIBR was performed using whole image(Whole)，only the object-region in ground-truth mask(Mask)，and image segments for JSEG and CSeg techniques(the subscript indicates the average number of segments).Precision-recall curves for retrieving images matching the colour class of the query image have been plotted in Fig.2 for all images as well as images in four object classes:cars，dresses，pot_glass，and shoes.While using image segments，all segments are used except for the query image，which uses either all segments(Regions)or segments in its ground-truth mask(ROI-Mask［Q］).

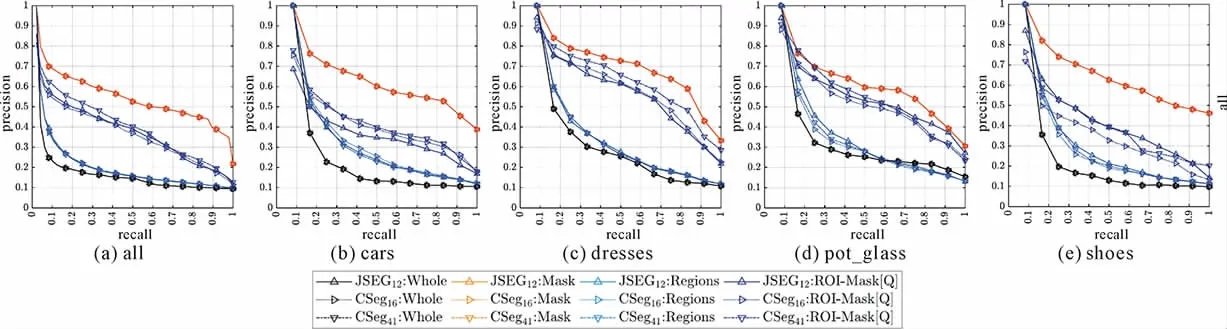
Fig.2 Precision-recall curve on eBay Dataset with JSEG12，CSeg16，and Cseg41.

Clearly，retrieval performance is better when image segments are used as the same with whole image provides a lower-bound.Performance with CSeg matches closely to JSEG irrespective of the average number of segments.Retrieval performance improves significantly when only the segments in the ground-truth mask of the query image is used for both CSeg and JSEG. Comparatively， CSeg outperforms JSEG in this case and the difference widens as CSeg produces more number of segments on average.Retrieval performance using only the object-region in ground-truth mask provides an upper-bound.

4 Conclusion

Making effective use of continuous surveillance video footage in real time is a challenge facing the world. The International Organization for Standardization(ISO)on Coding of Moving Pictures and Audio has identified intelligence as a future trend in the video surveillance industry and recommended video coding standards to facilitate“intelligent analysis that could be implemented in the camera side to analyse the uncompressed video directly.” High computational complexity of the existing image segmentation techniques and high coding complexity of their arbitrary-shaped accurate segment boundaries render them ineffective to meet the above challenge.CSeg has been developed to fill this gap with the minimum possible linear order computational complexity and approximated rectangular–shaped segment boundaries that can be encoded efficiently with a simple binary tree.