扩散形态算子在图像比较中的应用
段 汕,张 晔,张彬彬
(中南民族大学 数学与统计学学院,武汉 430074)
图像相似性研究在图像识别[1]、图像匹配[2]、图像比较等方面有着广泛的应用. 在Pyt′ev的形态学图像分析方法[3]中,将分片常函数作为二维图像Mosaic图像的模型空间,提出了基于投影算子的图像比较方法,通过建立各类相关系数对图像的相似性进行定量描述.在分片常函数的图像表示方式下,相关系数的各类指标依赖于对图像空间域的初始划分.对大多数图像来说,基于图像强度的分割相对质量较低,对噪声较为敏感,对高频噪声的干扰不能保持足够的稳定,相应算法的鲁棒性较弱,对图像相似性研究结果的准确性会带来较大的影响.
Vizilter在文献[4]中引入高维数据降维技术[5]的基本原理,在对数据不进行初始分割的情况下,对相关方法进行改进,提出了基于扩散映射建立相关系数的方法,通过扩散相关系数实现对图像相似性的度量,使得相关指示对于噪声更具稳定性.本文在以上工作的基础上,将Laplacian特征映射[5]和扩散映射[6]的方法应用于图像数据,通过对图像数据热核及扩散核相关问题的研究,提出了建立扩散形态算子及用于图像相似性比较的基本框架,证明了Pyt′ev形态分析理论中的投影算子及形态相关系数是扩散形态算子及扩散形态相关系数在马赛克图像模式下的特殊情形. 研究表明,在Pyt′ev形状分析及相关算法中,运用扩散形态算子替代形态算子可以建立更加广阔的扩散形态学基础理论.与此同时,文中还对相关算法具体实现方法和参数选择方式进行了适当改进,使得图像比较中的相关数据、实验结果得到一定的改善.
1 研究基础
1.1 形态相关系数
Pyt′ev所提出的图像形态学分析理论[3],是一种基于图像到形状的图像相似性研究方法,在这种理论下图像被模型化为分片连续的二维函数f(x,y):Ω→R,(x,y)∈Ω⊂R2:
(1)
其中F={F1,F2,…,Fn}是对空间域Ω⊆R2的划分,f={f1,f2,…,fn}是对应于划分F的图像强度向量;χFi(x,y)∈{0,1}是第i个子区域Fi的特征函数:
图像f(x,y)的形状定义为:
∀f={f1,f2,…,fn}∈Rn},
(2)
且F⊆L2(Ω).图像g(x,y)∈L2(Ω)在形状F上的投影具有如下形式:
在Pyt′ev的图像形态学分析中,图像g(x,y)与图像f(x,y)的相似程度通过基于投影算子PFg(x,y)的形态相关系数
(3)
进行度量,所描述的是图像g(x,y)与图像f(x,y)的形状F接近程度.
1.2 图像热核
以上所给出是两幅图像之间的形态相关系数.利用Laplacian特征映射原理[5],对于图像f(x,y)((x,y)∈Ω⊂R2)的数据集合V={(x,y,f(x,y))|(x,y)∈Ω},通过设计邻接关系准则,可产生V中点的邻接图,准则可基于图像类型进行设立. 一幅具有s×t个像素的图像需要用s×t维空间中的向量来表示,同一场景在不同条件下所获得的图像集合就是一种高维数据集合. 为了有效地处理这些数据,使用降维技术就显得十分必要. 降维是指将样本从高维观测空间通过线性或非线性映射投影到一个低维特征空间,从而找出隐藏在高维数据中有意义的低维结构. 基于Laplacian特征映射的非线性降维方法旨在保持高维观测数据局部结构的同时,使不在同一邻域内的点之间距离变得松驰,扩散映射通过在扩散过程中保持扩散距离进行降维. 扩散映射的主要思想是通过在数据集上构造的扩散图,利用扩散距离来描述数据间的相似度,使用一系列扩散核进行数据降维,从而避免高维数据矩阵进行特征分解的不稳定性和不可行性[7].
基于图像f数据集合V的邻接关系,可产生图像f的热核[4,5,8]:
hf(x,y,u,v):Ω×Ω→[0,1],
将其称为图像f的扩散形状,记为.图像f的热核一般具有如下特征:hf(x,y,u,v)≤hf(x,y,x,y),即自相似最大原则,且关于像素点具有对称性:hf(x,y,u,v)=hf(u,v,x,y),它是对数据间相似性的一种度量. 由Laplacian特征映射原理,数据集V上存在唯一的测量函数η,使得hf(x,y,u,v)=η(f(x,y),f(u,v)),函数η所描述的是V中数据点(x,y,f(x,y))与(u,v,f(u,v))在像素点(x,y),(u,v)∈Ω具有某种邻接关系条件下的相似程度,是对图像f(x,y)局部特征的一种刻画,以此信息用于表示图像f的整体信息.
2 扩散形态学的基本思想
2.1 扩散形态算子
图像f热核hf(x,y,u,v)的主要作用是描述数据点之间的局部连接性,捕捉数据的局部几何特征. 将热核正规化形成图像的扩散核:
H
(4)
其满足非负性、对称性,且
因此可假设
利用扩散核所包含的数据局部信息构建数据全局形态特征需要采用扩散映射的思想[6],定义:
D
(5)
称D为图像f的扩散形态算子,且对于任意图像g(包括图像f)都有‖Dg‖≤‖g‖.
将形态相关系数(3)中的投影算子PF替代为图像f的扩散形态算子D,引入扩散相关系数:
KD(g,
它给出了图像g与形状的一种相似度测量指标,且0≤KD(g,)≤1.
由扩散核H的性质,扩散算子D具有平滑功能,而‖Df‖≤‖f‖,故D不是投影算子,因此可假设D的平滑能力满足条件:DD(f,)≥KD(g,),这样将扩散相关系数的比:
KMD(g,
(6)
称为扩散形态相关系数,这里KD(f,)(≤1)是扩散算子D对于图像f自平滑能力的测量值,且0≤KMD(g,)≤1. 显然KMD是对KM的推广,当取为F且D取为PF时,KMD(g,)=KM(g,F),即当(6)式中的算子取为投影算子时,扩散形态相关系数(6)式即是形态相关系数(3)式.
若将图像单位化,即‖f‖=‖g‖=1,则有:
KMD(g,
由此可知‖Dg‖<‖Df‖(∀g≠f),即算子D对于图像的平滑作用与目标图像和图像f的相似程度相关.
如果能获得扩散算子D的特征值{λ1,λ2,…,λn}及其所对应的特征函数{φ1(x,y),φ2(x,y),…,φn(x,y)}:
Dφi(x,y)=λiφi(x,y),i=1,2,…,n.
=span{φ1(x,y),φ2(x,y),…,φn(x,y)}.
(7)
2.2 扩散算子的一种特殊情况
在以上所讨论的扩散形态算子的理论框架下,依据Laplacian特征映射中0-1加权函数建立的思想,考虑图像f热核hf的一种简单且特殊的形式:
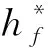
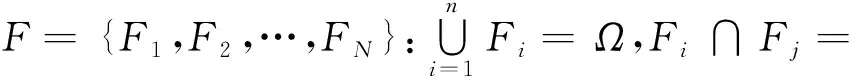
由(4)式其扩散核
且对(x,y)∈Ω,必存在1≤k≤n,使得(x,y)∈Fk,故有:
这里S(·)表示目标对象的面积,故
或表示为:
由(5)式,其对应的扩散算子:
φi(x,y)=χFi(x,y),i=1,2,…,n,

=span{χF1(x,y),χF2(x,y),…,χFn(x,y)},
即由(2)式所给出的图像f的马赛克形状F,图像f则具有(1)式的形式,且
与此同时,由

3 建立图像热核的方法
对于图像热核的正规化处理产生了一个线性光滑的扩散形态算子D,热核的经典形式与扩散距离相关,以下着重讨论图像热核及扩散核建立的基本方法.
对于二维图像f(p),p=(x,y),扩散形态算子D的建立可以直接从图像数据集合中点间距离和热核的经典形式[4]
(8)
入手,其中d(p,q)是数据集中点p,q之间的基本距离,ε>0为控制指数函数衰减速度的调节参数. 以此为基础的扩散形态算子,在Pyt′ev的形态分析方法中对应于基本距离的一种特殊选择:

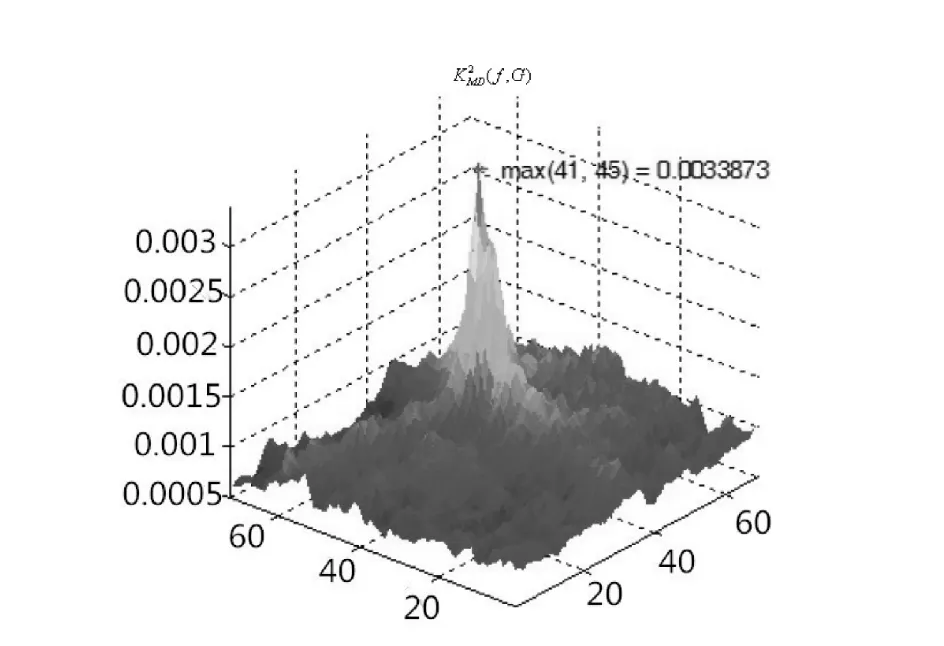
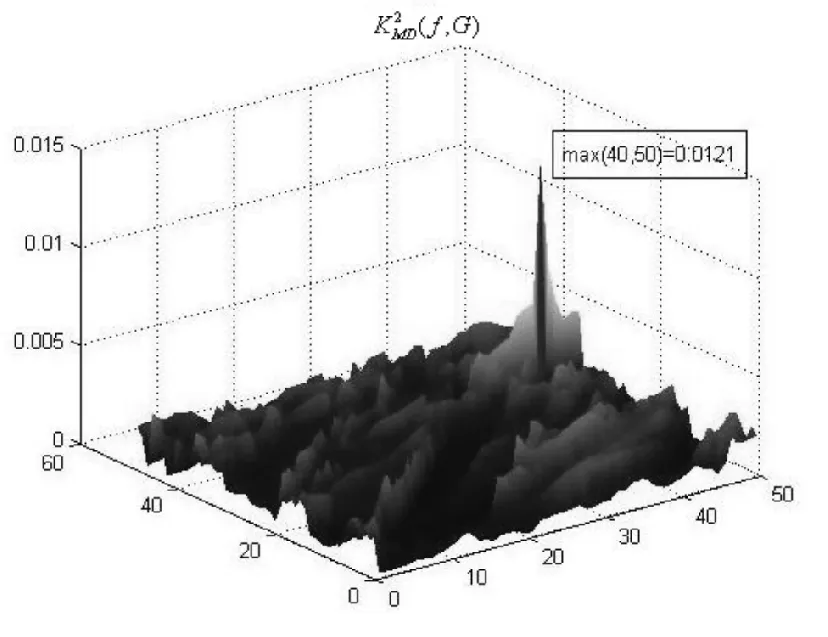
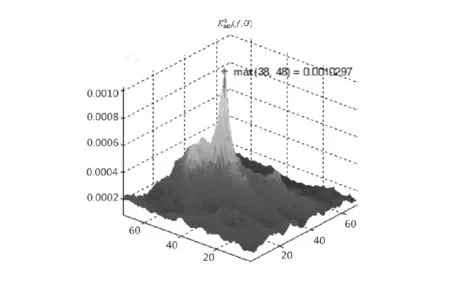
考虑具有s×t个像素的二维图像f(p)在像素点p的l×l邻域,这里奇数l< d(p,q)=‖v(p)-v(q)‖, 或设计为平均Hausdorff距离[9]: (9) 但即使v(p)在合理的邻域尺度设置下,范数运算也会产生时间上极大的消耗. 为提高计算效率,采用局部二值模式[10]LBP特征向量(矩阵)替代v(p),对基于范数的度量方法进行相应的修正,以此减少时间上的消耗. 对于点p的邻域v(p),利用LBP算子所产生的v(p)的LBP二进制特征模式B(p),及v(p)的平均值m(p),将范数替代为: ‖v(p)-v(q)‖~β|m(p)-m(q)|2+dham(B(p),B(q)), 其中dham为汉明距离,β是一个调节权重. 由此得到平均Hausdorff距离(9)式的修正形式: 及图像f热核的具体形式: (10) 以此便可构造出扩散形态算子D. 实验的目的在于测试扩散形态算子及扩散形态相关系数在图像比较中的作用,并将文中所提算法与已有算法和实验结果进行分析比较,以说明本方法的有效性.图1给出了二组TV和IR测试图像.已有算法中,图1(c)所表示的图像和图1(b)的表示的图像的扩散形态相关系数的分布如图2所示.图3给出了基于(10)式的扩散算子中,ε=0.01、l=3时得到的Housdorff距离模式下的扩散形态相关系数分布. 图1 原始图像及用于匹配的图像Fig.1 The original image and the image used to match 图1(f)所示图像和图1(e)所示图像依据原有算法的扩散形态相关系数分布如图4所示.在取ε=0.01、l=3以(10)式为热核的扩散形态相关系数分布如图5所示. 图2 原始算法下地形图像的分布图Fig.2 Distribution of terrain image under the original algorithm 图3 改进算法后地形图像的分布图Fig.3 Distribution of the terrain image after improving the algorithm 图4 原始算法下细胞图像的分布图Fig.4 Distribution of the cell image under the original algorithm 图5 改进算法后细胞图像的分布图Fig.5 Distribution of the cell image after improving the algorithm 上述实验结果,在选取不同的距离、邻域尺度以及控制指数衰减参数ε,得到了不同的扩散形态相关系数的分布以及不同分布中相关系数的峰值,其相似效果可以通过均方相关系数统计的二维相关函数C(x,y)的性噪比(SNR)和全局最大相关值C1和次最大相关值C2超越率E进行度量: 其中μ和σ分别为相关函数的均值和方差. 图1~图4中的各峰值、性噪比、超越值分别见表1和表2.相关数据的比较说明,本文相关算法下所获得的数据优于原有结果. 表1 不同算法得到的地形图像相关系数 Tab.1 The correlation coefficient of terrain image obtained by different algorithms 相关系数K2MD(f,G)最大值性噪比超越值图2相关系数0.003399.98094.6698图3相关系数0.0121414.12754.8646 表2 不同算法得到的细胞图像相关系数 Tab.2 The correlation coefficient of cell image obtained by different algorithms 相关系数K2MD(f,G)最大值性噪比超越值图4相关系数0.0010310.22863.8530图5相关系数0.0043510.94324.7541 由表1可得,图2和图3相关系数的最大值(峰值)分别为0.00339和0.01214,而且性噪比的值图3为14.1275大于图2的9.9809,说明扩散形态学方法的改进算法比原始算法对于噪声更加稳定,更能准确地度量两幅图像的相似度.同理表2中图4和图5相关系数的最大值(峰值)分别为0.00103和0.00435,而且性噪比的值图5为10.9432大于图4的10.2286,也说明了扩散形态学方法的改进算法对于相似性的研究要优于原始算法.因此,扩散形态学方法的改进算法能更有效地应用于图像相似性研究. 本文对扩散形态算子进行了基础性研究,通过改进获取热核的相关算法,使得算子在结构上更具一般性,在应用上更具稳定性,为扩散映射在图像相似性研究领域提供了一个研究方向.4 实验结果及分析




5 结语

