超声速来流下混合流动控制射流角度影响数值研究

王旭东, 高 峰, 朱柏银, 张 涵

(空军工程大学 防空反导学院, 陕西 西安 710051)

0 引 言

在高速吸气式飞行器中，边界层流动分离现象一

直是发动机工作性能提升的一大阻碍[1〗。诸多研究者对超声速进气道/隔离段内流场流动特性的研究结果表明，边界层流动分离会导致流场畸变增加、总压损失增大甚至发动机不启动等[2-3]。因此，对边界层流动分离及其控制进行研究受到广泛关注。

目前，已有的可有效延缓边界层流动分离的方式有抽吸、等离子体控制、微型涡流发生器和微型射流涡流发生器等[4-7]，由于可靠性高以及系统复杂性小，微型涡流发生器和微型射流涡流发生器具有广阔的应用前景[8]。Shinn等[9]发现当来流马赫数由2.0降到1.8时会出现激波串被推出进气道引发不启动现象，但在加入微型涡流发生器时，进气道恢复了启动；Henry[10]采用数值模拟的方法研究了微型射流产生的流向涡对边界层的作用，指出俯仰角在30°、偏航角60°时使得壁面摩阻增大最多，边界层最不容易发生分离。

近年来，人们发现微型斜坡与微型射流组合成的混合流动控制器对流场改善作用远优于二者的单独作用[11]。Valdivia[12]等在微型涡流发生器后部加入微型射流涡流发生器阵列后，在保证进气道处于稳定启动状态下，使最大背压提升32%，隔离段内压强震荡降低34%。Vyas[13]研究了在正激波/边界层干扰作用下的混合流动控制器阵列进行风洞实验，对比了射流质量流率的影响，研究表明，射流质量流率为来流的1%与尺寸较大的微型涡流发生器组合可产生更强的流向涡，边界层动量增加也最明显。

但微型射流涡流发生器的射流角度对混合流动控制器的流动控制特性及隔离段流场改善的作用尚不明确，本文在前人研究的基础上，通过分析改变射流俯仰角和偏航角后流场内性能参数的变化来研究在高出口反压工况下混合流动控制器的流动控制规律及其作用机理。

1 计算模型

计算模型为总长377.1 mm，进口截面为30 mm×25.4 mm的矩形自由通道，其中隔离段总长227.1 mm。为使来流附面层充分发展，在隔离段前设置150 mm长的附面层发展段。微型涡流发生器的后缘高度为h=2.7 mm，前缘宽度c=5.84h，轴向长度l=6.57h，放置于隔离段入口处，设置微型涡流发生器前缘中心为坐标轴原点。射流喷孔直径d=1.4 mm，微型涡流发生器与射流喷孔的距离为7.5 mm，计算模型见图1。来流马赫数Ma=2.0，总温T0=300 K，总压p0=360.224 kPa，静压p=48.433 kPa，设置出口背压pout=167.58 kPa。射流总压p0=1379 kPa，总温T0=286.7 K。

为深入研究混合流动控制器中射流角度变化对流动控制特性的影响，本文设置9个算例进行研究。为验证混合流动控制器不同射流俯仰角抑制流动分离效果差异，在保持偏航角为0°不变的情况下，射流俯仰角θ分别取30°、45°、60°和90°。为研究射流偏航角对隔离段性能的影响，保持俯仰角为30°不变，偏航角β分别取0°、15°、30°、45°、60°和90°。

本文采用FLUENT软件对隔离段三维流场进行数值模拟，选用可压缩修正的SSTk-ω湍流模型，二阶迎风格式离散，设置来流为理想气体，气体黏度采用Sutherland方程描述，并选取基于密度的耦合显式求解器求解稳态问题。由于来流附面层非对称，附面层发展段上壁面设置为滑移壁面，其余壁面为绝热无滑移壁面，入口来流附面层厚度为5.43 mm。计算域网格用采ICEM软件进行结构化网格划分，为保证计算的精确度，对近壁面处、微型涡流发生器及射流附近进行网格加密处理，保证第一层网格为1×10-5m，壁面y+在5以下，符合SSTk-ω湍流模型对壁面网格密度的要求。网格总量约为300万，局部网格如图2所示。

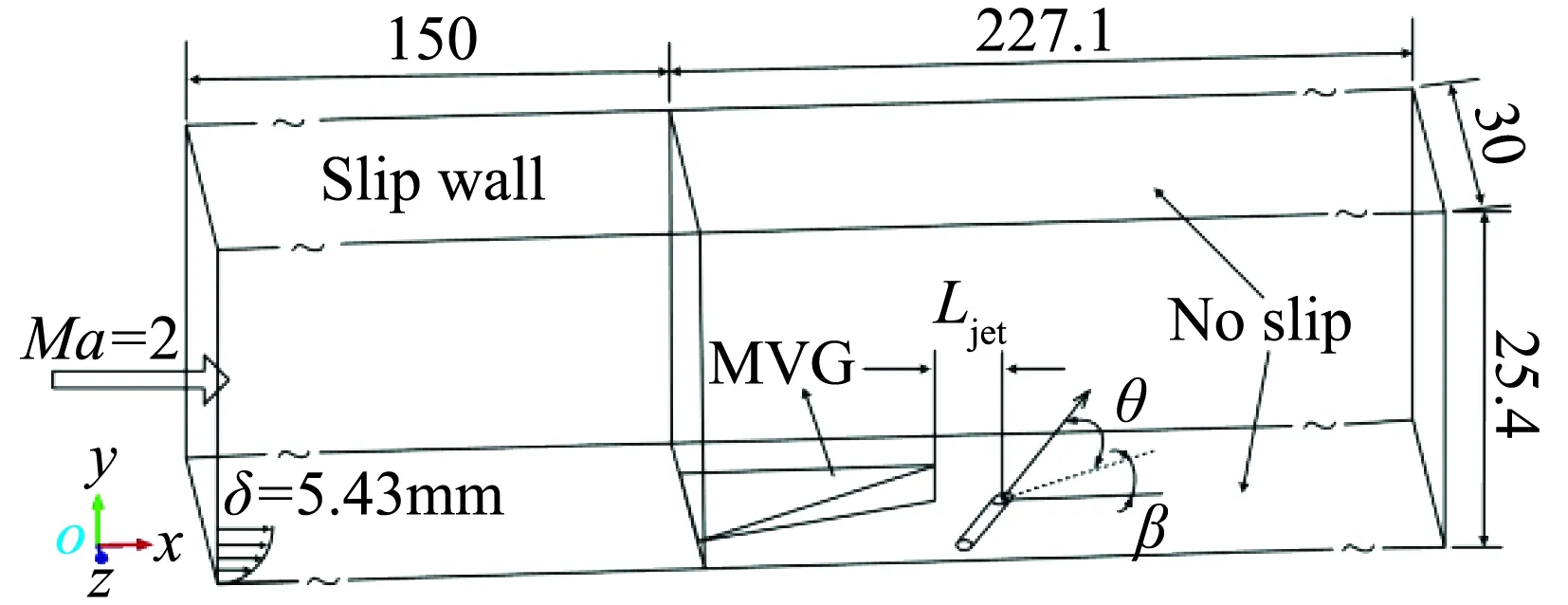
图1 计算域结构示意图(单位：mm)Fig.1 Geometry of calculation model

图2 局部网格示意图Fig.2 Typical internal grid

为验证本文选用的SSTk-ω湍流模型对本文物理模型的适用性，对文献[14]的实验进行数值模拟计算。来流马赫数Ma=2.5，总温T0=280 K，总压p0=380 kPa，静压p=21.6 kPa，计算域的尺寸为133.2 mm×73.2 mm×13.2 mm，入口为压力入口边界条件，其余为出口边界条件。微型涡流发生器后缘高度为4 mm，腰长28.3 mm，顶角为48°。从图3的下壁面流线与实验油流图的对比结果来看，数值计算方法将壁面流场拓扑结构较为精确地刻画出来，流场在尾部发生二次分离产生二次涡，同时形成的反向旋转主涡对的痕迹在模拟结果中也可观察得到，且与实验纹影图较为吻合。图4是微型涡流发生器后侧20 mm中心线处(z=0 mm)以及展向z=12 mm处流向速度的数值模拟与实验数据对比图，由于受尾部涡环的影响，z=0 mm处在局部低速区内，因而随y增加，速度曲线呈现图中变化趋势，展向z=12 mm处的流场基本不受扰动。数值计算结果与实验值吻合较好，本文选取的湍流模型合理。

图3 下壁面流场数值模拟与实验对比图Fig.3 Comparison between the experimental data and simulated result of surface flow topology

为保证计算有效性，在各项指标的计算残差均在10-4以下，并且在残差曲线保持稳定不变的状态下判断其为收敛。为验证计算网格的有效性，特增加了对网格无关性检验验证。为验证本文选用的300万网格的有效性，本文对基本构型流场选用200万(Coarse)、250万(Medium_1)、300万(Medium_2)、350万(Fine)四种数量网格算例并采用隔离段内上壁面中心线上的压强作为表征参数对网格的无关性进行检验。如图5所示，随着网格数的增大，压强曲线越来越贴近，300万和350万网格所得压强值的曲线基本重合，说明300万数量的网格已经可以满足计算精度的要求。考虑到计算成本的限制，本文算例均采用300万左右数量的网格。

2 计算结果与分析

2.1 射流俯仰角对流动控制的影响

射流俯仰角θ过大时，射流动量的法向分量容易造成流向涡穿透边界层，引起控制作用下降；而射流俯仰角过小时，流向涡会因为完全嵌入在边界层内部而沿流向迅速衰弱，导致其流向控制区域急剧减小。因此，弄清混合流动控制下射流俯仰角对控制作用的机理至关重要。

为描绘混合流动控制器周围流场结构的三维特性，现结合空间流线、截面流线和马赫数分布云图对混合流动控制器附近区域的主要流场特征进行描述。图6为对称面和x=35mm、x=60mm处马赫数云图、流线图。由图可知，微型斜坡上侧形成一个分离包，来流与之撞击形成分离激波与射流产生的斜激波对来流起到初步压缩作用。比较射流上侧马赫数分布，发现射流俯仰角越大，与来流相互作用越强，对来流的阻滞作用越强。观察三维流线，底层来流绕过微型斜坡形成一对方向旋转的流向涡，原本无旋拧的射流，在流向涡的卷吸作用下，亦产生旋拧作用，从而使混合流动控制器可以产生强度更大的流向涡，更有利于改善底层流场质量。比较射流角度变化对流线空间分布的影响，射流俯仰角越小，流线在空间分布越集中，同时从截面流线图看出，形成的流向涡的分布越远离壁面。

由图7的截面流向速度云图和流线图看出，四个算例的回流区与入口的距离基本相同；θ=30°时回流区范围最大，θ=45°与θ=60°的各参数无明显差异；θ=90°的角涡强度最大。由此可以得出，俯仰角的变化仅小幅度改变角区低速回流区的轴向位置，但较大改变了回流区范围和角涡强度，其中θ在45°和60°附近时，回流区范围最小；θ过小时，回流区范围较大，θ越大，角涡强度越强。

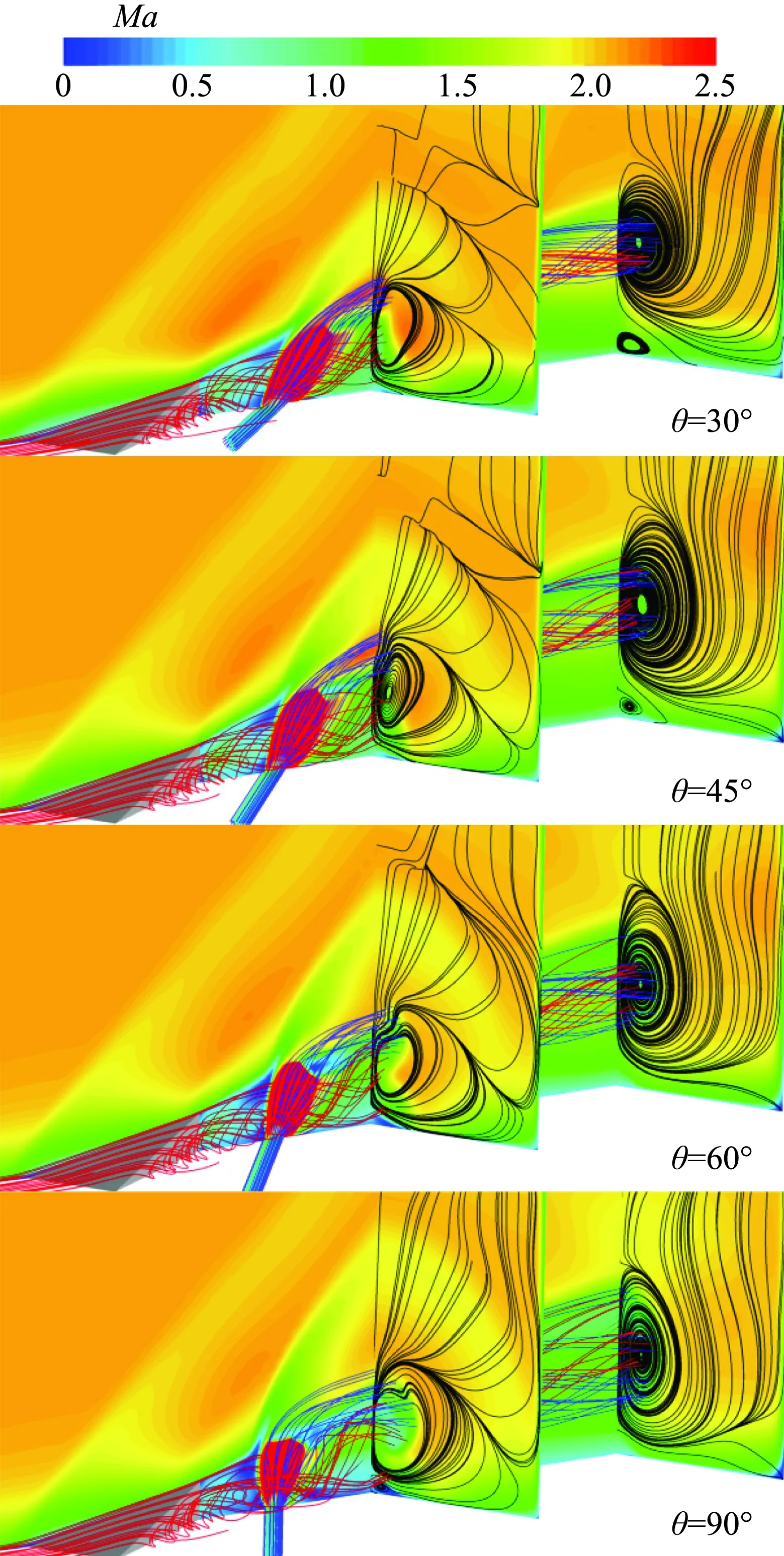
图6 对称面和x=35 mm、x=60 mm处马赫数云图、流线图Fig.6 Ma number contours and streamlines at symmetry plane, x=35 mm and x=60 mm

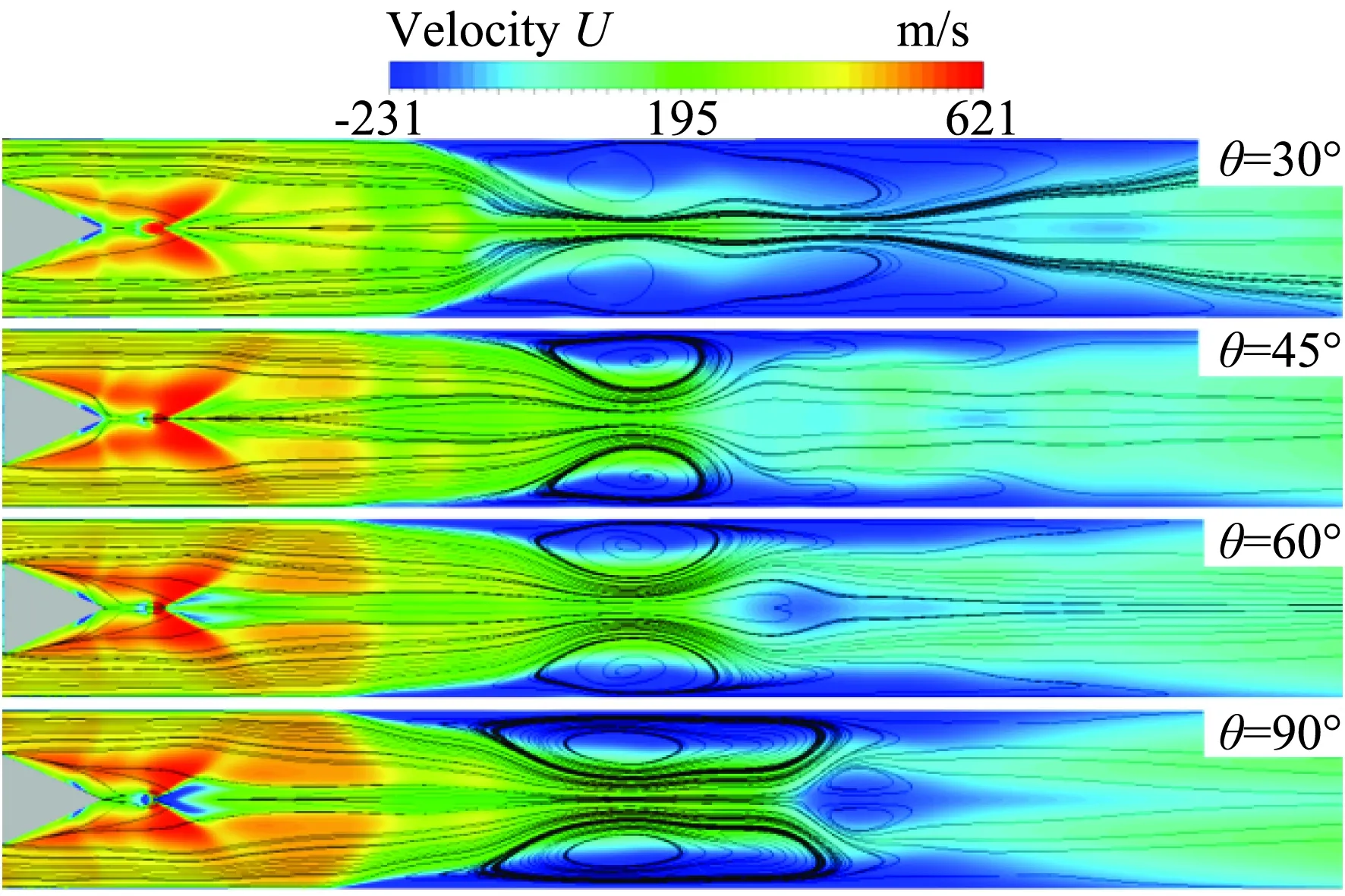
图7 y=0.1 mm截面流向速度云图和流线图Fig.7 U contours and streamlines at y=0.1 mm

图8给出了射流不同俯仰角下的流向涡核心高度H(流向涡中心与下壁面距离)沿流向变化情况。图中表明，流向涡沿流向逐渐向上飘起，其中在接近隔离段出口处，θ=30°的流向涡已经接近上壁面，并且涡核高度明显高于其他俯仰角。流向涡高度过高，势必会失去对底层低动量流场的控制，这也解释了图6中θ=30°存在大范围低速回流区的现象。θ=45°与θ=60°无明显差别。θ=90°与θ=45°、θ=60°的涡核高度在x=150 mm之前基本持平，之后明显降低。与单独的射流式涡流发生器不同，在x=20 mm处，θ=30°的H=1.36 mm高于θ=90°的H=1.61 mm，但在此之后，俯仰角越大，流向涡核心高度反而越低。分析原因，高俯仰角的射流在y方向的速度分量较大，产生的流向涡会在短距离内穿透到微型涡流发生器上方的高速流场区域，高速流体对流向涡冲击作用明显，y方向动量的损失相对于小俯仰角的射流要大，随着流动的继续，小俯仰角射流的流向涡在y方向抬升起来后，已经处于流速较缓的流场区域，因而动量损失较小，流向涡抬升也更快。

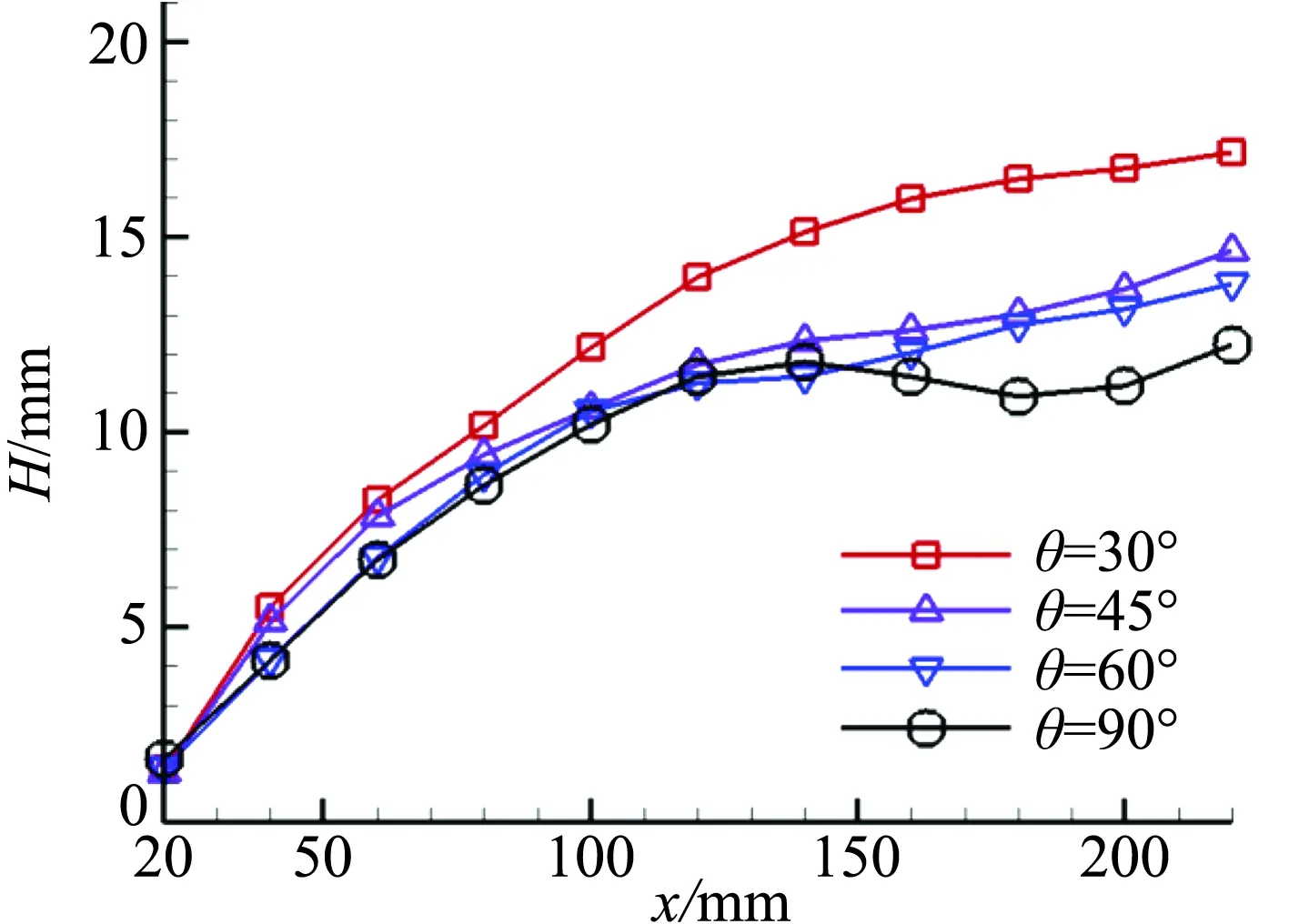
图8 涡核心高度沿流向变化曲线Fig.8 Height of streamwise vortex along x axis

壁面摩擦系数Cf=2τw/(ρu2)是用来衡量涡旋对边界层控制作用的重要参数[15]，较大的Cf表明动能较高的流体被涡旋带到壁面附近，使边界层对抗分离的能力获得提高。为利于比较，采用入口处Cf∞值进行无量纲化处理，对比图9的壁面摩擦系数变化趋势，x/h=7.4的Cf值由对称面(z=0 mm)到壁面(z=15 mm)出现波谷，之后由于流向涡的作用Cf上升至最高，低扰动区的Cf值趋于平缓，侧壁面处最低。流场较远处(x/h=29.6)Cf展向分布相对均匀，由于角区低速回流区影响，靠近侧壁面的Cf值较低。比较俯仰角的影响，θ=30°的Cf值最低，θ=45°和θ=60°的Cf值相对最高。

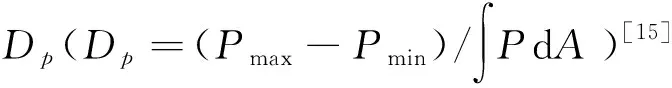
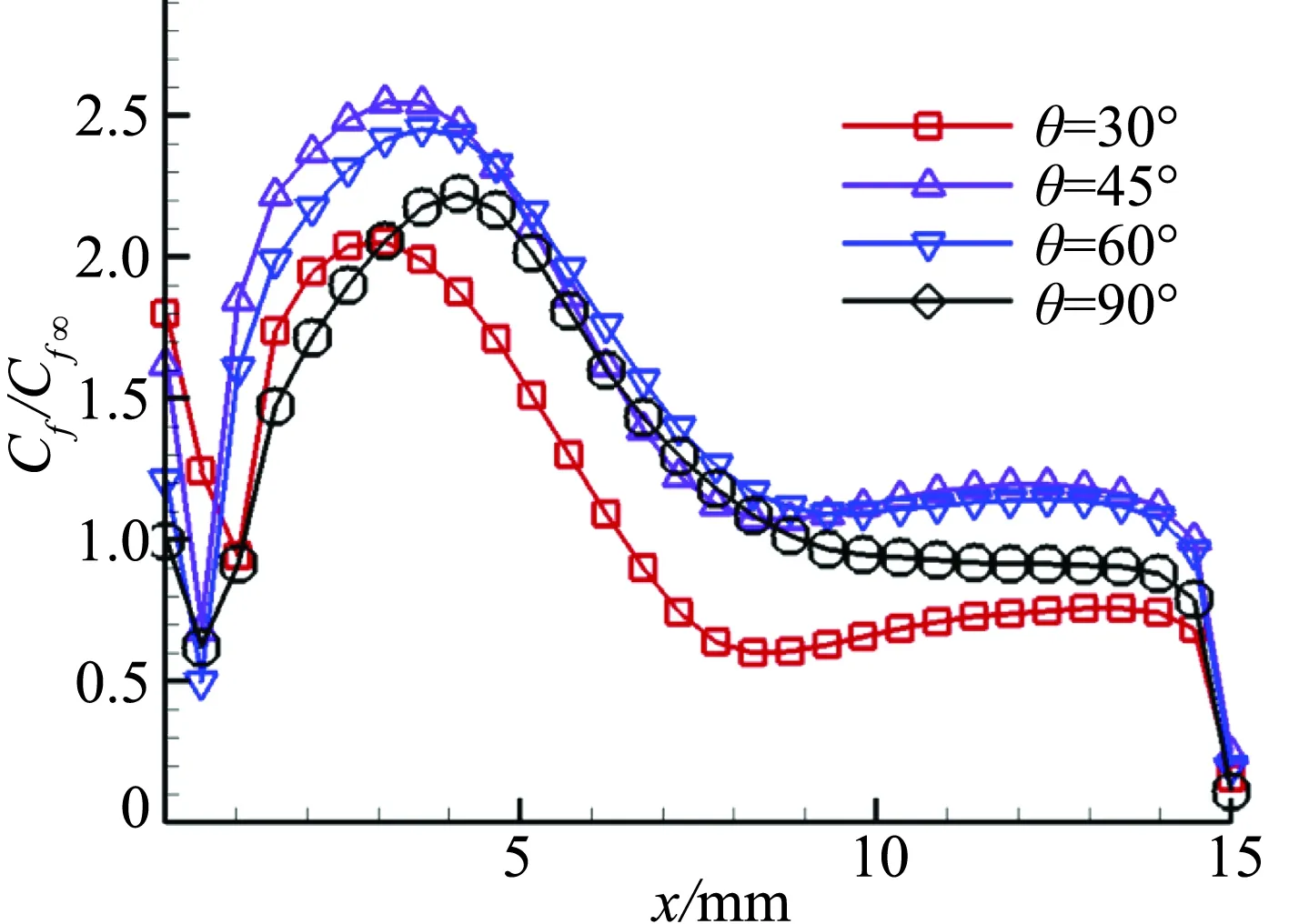
(a) x/h=7.4

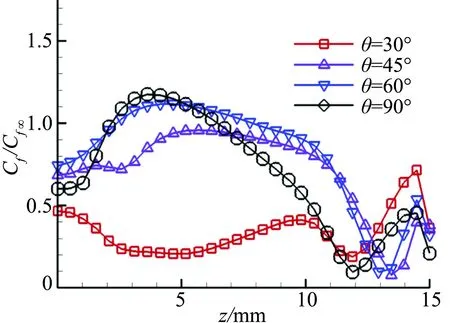
(b) x/h=29.6

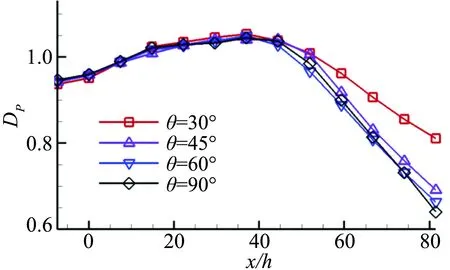
图10 总压畸变指数Fig.10 Total pressure distortion

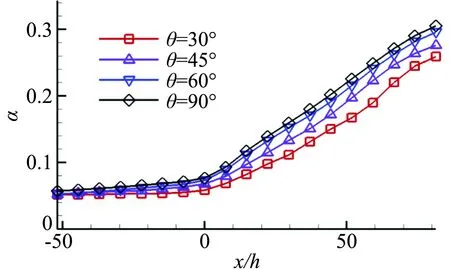
图11 总压损失系数Fig.11 Total pressure loss coefficient

2.2 射流偏航角对流动控制的影响

文献[15]指出，采用一定偏航角的微型射流对流向涡控制作用有利，其中偏航角θ=30°，俯仰角β=60°时产生的流向涡控制作用最优异，但与微型涡流发生器组合时的控制作用尚不明确。为直观比较采用不同偏航角射流控制下流场的抗反压能力，对照图12各算例上壁面压强云图可以发现，在x=40 mm和x=50 mm处，各算例均存在两个局部高压区，这是由于微型涡流发生器前缘、后缘形成的两道斜激波打在上壁面处形成的。随着偏航角的增加，压强前锋在x方向的位置先增大后减小，激波串长度先减小后增大，说明抵抗反压能力随偏航角的增加呈现出先增后减的趋势，其中β=45°时的高压区最远离入口，长度也最短。此外，偏航角越大，压强云图的不称性就越明显，尤其是β=60°和β=90°时，高压区明显有向射流方向的另一侧集中的趋势。

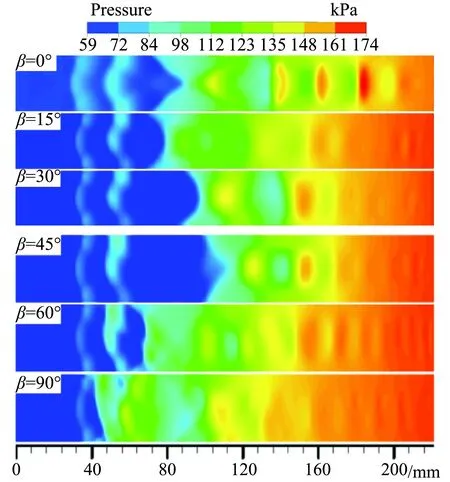
图12 上壁面压强云图Fig.12 Pressure contours at upper wall

提高射流偏航角可以有效增强射流与来流的作用，但不一定能改善对底层流场的控制作用，对照图13的流向速度云图和流线图发现，适当取β值可以有效延迟回流区的形成，如β=45°时，回流区在x=96mm处才开始形成，相对β=0°要延迟了28mm，但继续增加偏航角却使回流区向前传播，低速区范围迅速扩大；与压强云图表征一致，流场的不对称性亦明显增加，近壁区流场质量变差。

为直观的观察出不同偏航角射流产生的流向涡在yz平面上的变化以及流场内扰动程度，图14给出了x/h=14.8、29.6和55.6截面流线图、湍动能云图。观察发现，相比无偏航角，有偏航角射流产生的流向涡明显的不对称，并且射流偏航角的另一侧流向涡的强度和作用范围明显要大，随着流动的继续，强度较小的流向涡逐渐衰减消失，部分控制性较差的流场，角涡逐渐占主流。从下壁面角区的湍动能云图看出，除β=45°之外的角区高湍动能区范围几乎占据流道的一半，湍动能越大，表明流场的紊乱程度越剧烈，动能损耗越大，底层流场的流动性较差。同时发现，β=45°流场上壁面角区的高湍动能范围较其他偏航角稍大，但整体的高湍动能区面积最小。

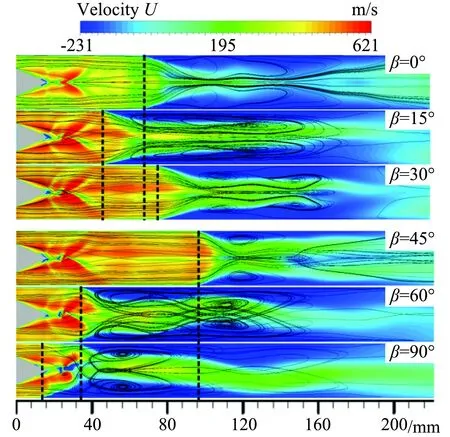
图13 y=0.1mm截面流向速度云图和流线图Fig.13 U contours and streamlines at y=0.1mm

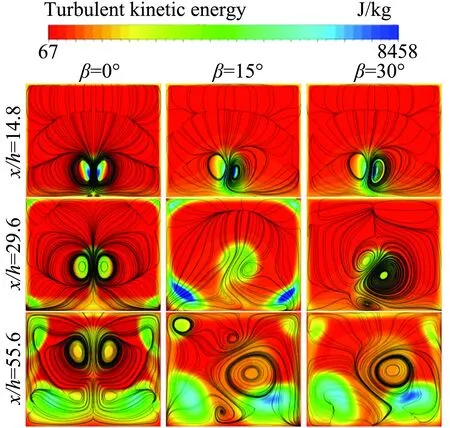
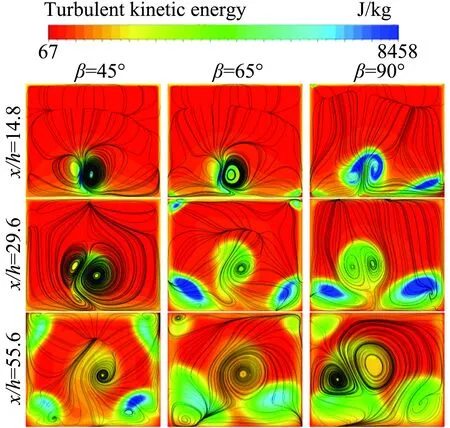
图14 x/h=14.8、29.6和55.6截面流线图、湍动能云图Fig.14 Turbulence kinetic energy contours and streamlines at x/h=14.8、29.6, and 55.6

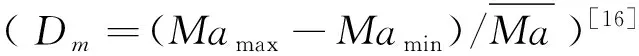
对照图16中各算例的沿流向总压损失曲线，可以很直观的得出总压损失随着偏航角的增加而增加的结论。由于偏航角的增加，射流在z方向的速度分量越大，射流与高速来流的作用增强，进而导致了总压损失的增加，所以在选择混合流动控制的射流偏航角时，可以适当选择较小的偏航角以达到综合控制性能的最优化。

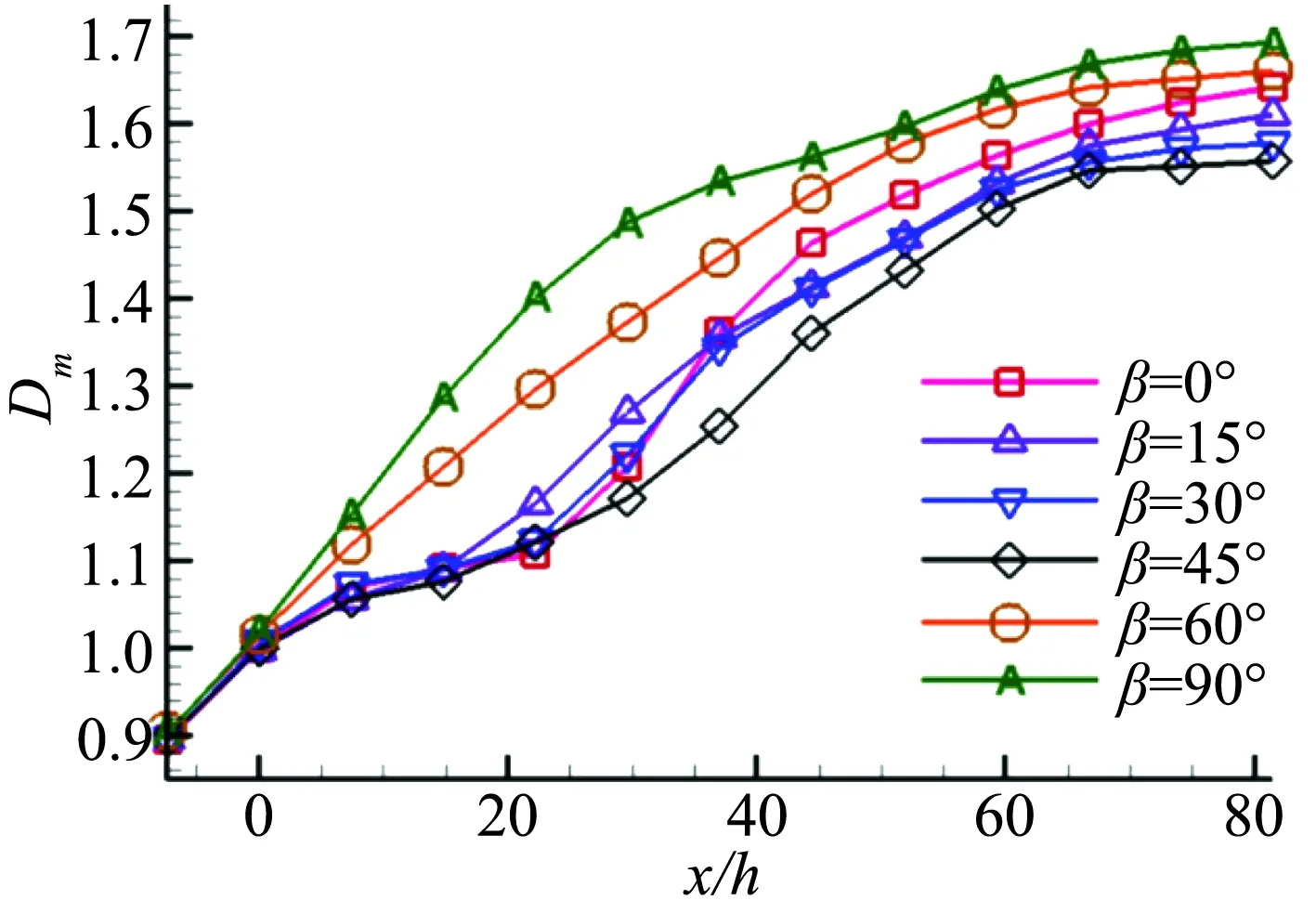
图15 马赫数畸变指数Fig.15 Ma number distortion

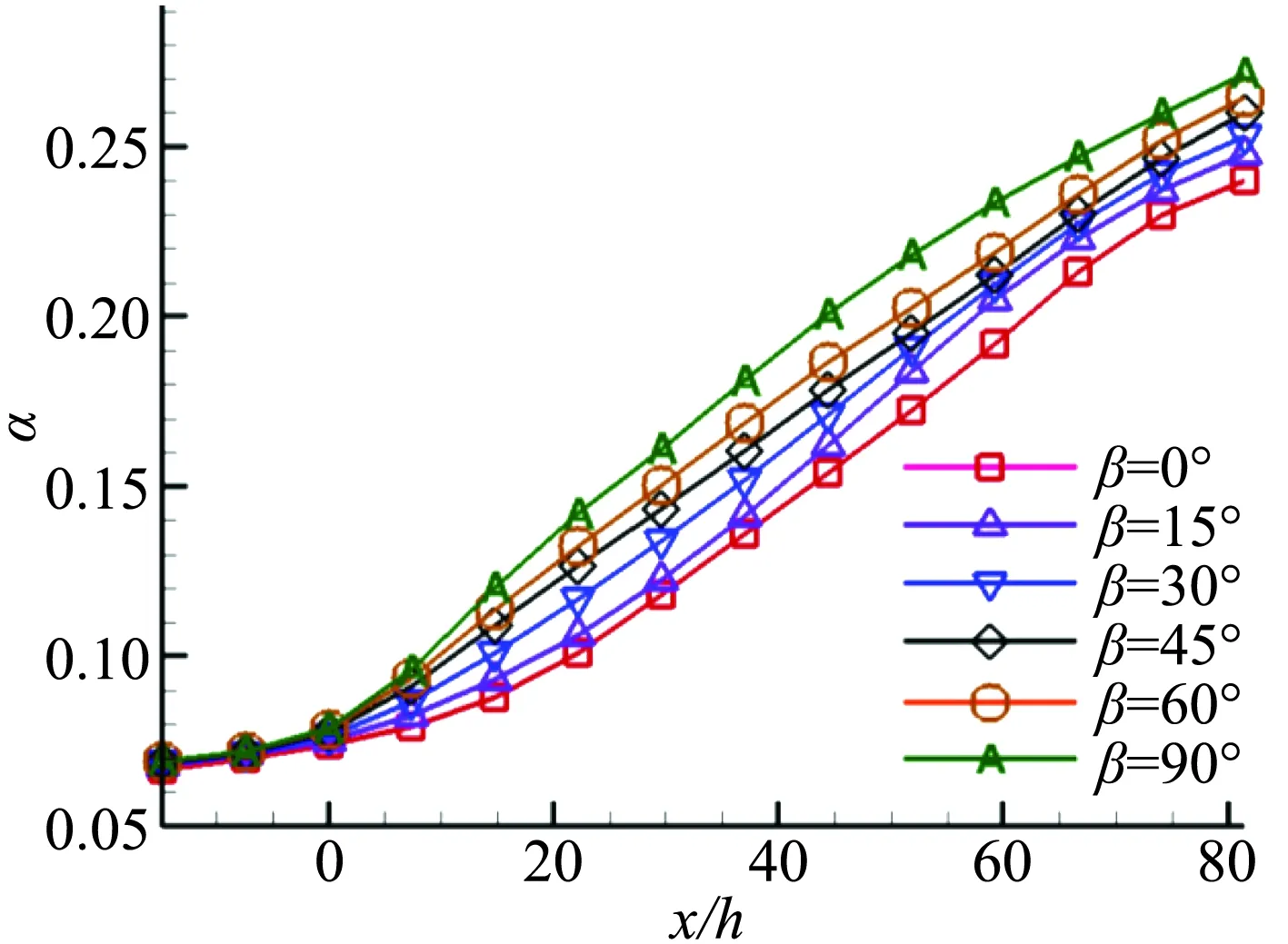
图16 总压损失系数Fig.16 Total pressure loss coefficient

3 结 论

本文通过数值模拟的方法对来流Ma=2.0条件下的隔离段流场进行数值模拟，研究微型涡流发生器与微型射流涡流发生器组合成的混合流动控制器的流动控制特性，着重比较了不同射流俯仰角和偏航角对流动控制规律的影响，分析了流动控制机理。研究发现：

1) 在给定射流位置时，射流俯仰角的变化仅小幅度改变角区低速回流区的轴向位置，但对回流区范围以及角涡强度有较大影响，其中θ取45°和60°时，回流区范围最小。俯仰角越小，总压畸变指数越小。

2) 取定射流俯仰角为30°时，偏航角的改变会对组合控制性能产生较大影响，随着偏航角的增加，隔离段抗反压能力呈现先增强后降低，底层流场质量和整体流场质量亦先提高后下降，偏航角过大会导致流场的明显不对称。综合比较，偏航角取45°时的流场质量以及抗反压能力最优异。

3) 由于微型涡流发生器上方高速流场的冲击，射流俯仰角越大，组合控制产生的流向涡高度反而越低。采用较小的俯仰角和偏航角可有效降低总压损失。

由于超声速进气道内壁面绕流的复杂性，采用RANS方法难以捕捉尾部涡环等流场精细结构，因此在对混合流动控制器改进隔离段性能的研究中难以分析出微型涡流发生器与微型射流涡流发生器的流向涡的耦合作用，下一步可以采用大涡模拟的方法将研究的重点放在混合流动控制的机理上面来。