核心素养视域下小学生运算能力的培育
江苏省昆山市千灯镇炎武小学 黄仁华
运算能力是小学数学学科的核心素养之一,在小学阶段,培育运算能力的重要性不言而喻。发展运算能力有助于学生代数思维的发展,有利于学生数感的形成和发展,而运算能力并不局限于数的计算,更兼具观察、理解、想象、推理等综合能力的相互渗透、相互支持。本文试着探讨在核心素养视域下培养学生运算能力的教学策略与途径。
一、充分利用几何直观,促进理解
心理学家认为:直观是从感觉到的具体对象背后发现抽象的能力。立足教与学的实际,小学阶段切合学生年龄特点的几何直观主要是直观感知和直观理解水平,利用几何直观可以帮助学生构建逻辑支撑,促进对运算的理解。
1.几何直观,建构规律模型
例如,苏教版四年级下册《运算律》,在教学乘法分配律时,可以将教材的素材改为如下情境(图1),这样将物品的计算和面积的计算情境整合,丰富学生的直观表象,在此基础上将长方形的长和宽改为其他数字,初步感受乘法分配律的外在结构和内在联系,丰富表象逐步抽象,最后将长和宽改成字母,建构完整的乘法分配律的几何模型,加深对乘法分配律的直观理解。
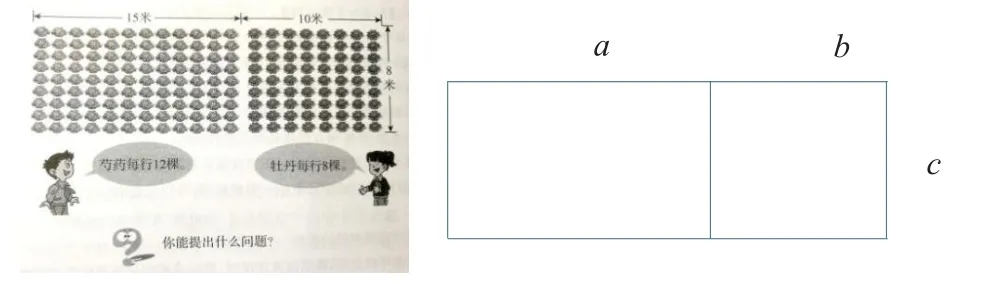
图1
在教学运算律的过程中,教师稍加引导,就能将学生的几何直观水平提升至直观理解水平,让学生经历“数学化”的过程,从本质上理解运算律,构建运算规律的直观模型,助力学生寻求合理简洁的运算途径解决问题。
2.数形结合,厘清运算本质
以“形”明“理”,能够将隐形的算理显性化,将实物进行半抽象,让学生直观地感受运算的本质,再抽象成算式计算,真正明白其中的道理。
例如,教学2+3=,对于低年级学生的运算学习,需要帮助学生建立丰富的直观表征,从观察、操作、思考中凝练出“部分—部分—整体”的模型(图2),通过数形结合的过程,厘清“2+3”的本质,促进运算能力的提高。
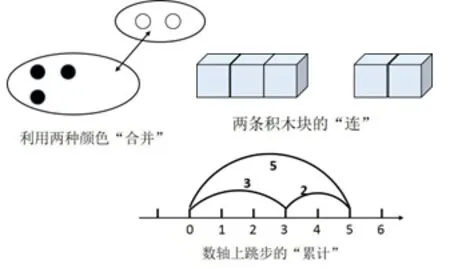
图2
二、有效融合算理算法,有机统一
算法解决的是“怎样算”的问题,而算理是解决“为什么这样算”的问题,两者相辅相成,学生只有真正明白了运算中的道理,才能真正理解和掌握算法,理解不同数域运算中算理的一致性。在运算的教学中有机融入算理的教学,让学生不仅明了程序性的计算过程,更理解为什么这么算。
1.融合生活经验,理解算理
例如,苏教版三年级下册《两位数乘以两位数(不进位)》的教学中,在学生交流想法时,着重关注将12分成10和2的方法。这是“生活数学”,学生出于经验的表达,教师应该记录下来,这也是算理的雏形。在交流竖式计算中,讨论每一步计算的结果表示什么,与“生活数学”的表达相互沟通,让学生经历“数学化”的过程,更好地将“学校数学”理解透彻。

在数学学习中,学生往往有丰富的生活经验,对于运算也有诸多想法,教师需要让学生充分表达想法,更好地了解学生知识的生长点,将学生的经验与数学知识有效链接,促进学生对算理的理解,更好地发展学生的运算能力。
2.沟通新旧知识,明晰算理
运算教学中不能使算理形式化、格式化,更不能让算理成为学生背诵的一句话,要结合已有知识进行有效沟通联系,真正挖掘为什么这么算,才能提高学生的运算能力。
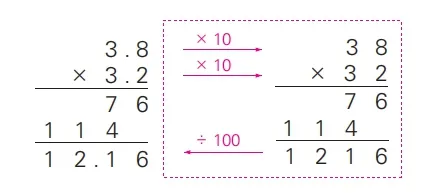
例如,苏教版五年级上册《小数乘小数》的教学中,学生已有小数乘整数和一个数乘以10、100、1000……等旧知,可以放手让学生自主探索3.8×3.2的算法。在学生充分的交流中总结:第一步,按整数乘法的计算方法进行计算,这是旧知;第二步,看因数有几位小数,积的小数位数是因数的小数位数的“和”,其背后的原因就是按整数乘法算时,3.8和3.2均扩大10倍,所以积要缩小100倍。通过学生的观察、联想、推理,进而总结出积的小数位数是因数的小数位数的“和”。在沟通旧知、归纳总结的过程中,提高了学生运算的能力,同样发展了推理、抽象等核心素养。
三、整体构建知识框架,形成体系
运算教学贯穿小学教学的始终,需要教师从整体上把握运算知识的脉络,清楚运算内容的前后联系,抓住各个阶段运算知识的本质实施教学,立足阶段着整体,帮助学生建立良好的认知结构。
1.着眼整体,明确算理一致
例如,苏教版五年级上册《小数乘法》的教学中,小数乘以整数、小数乘以小数等知识环环相扣,最终建构完整的小数乘法的计算方法。在教学完小数乘法后,应该进行回顾对比,说说3.8×3.2,38×3.2,38×32,380×320的算法,认识到都是利用整数乘法的规则来计算的,进而明确算理之间的相通性,将小数乘法、整数乘法形成完整的知识体系,更好地内化算理。
2.理解含义,拓展认知视野
理解算式的含义,有助于学生正确理解运算过程,判断计算结果,提高学生运算能力,还可以拓展学生认识分数、比等涉及数的概念性知识。
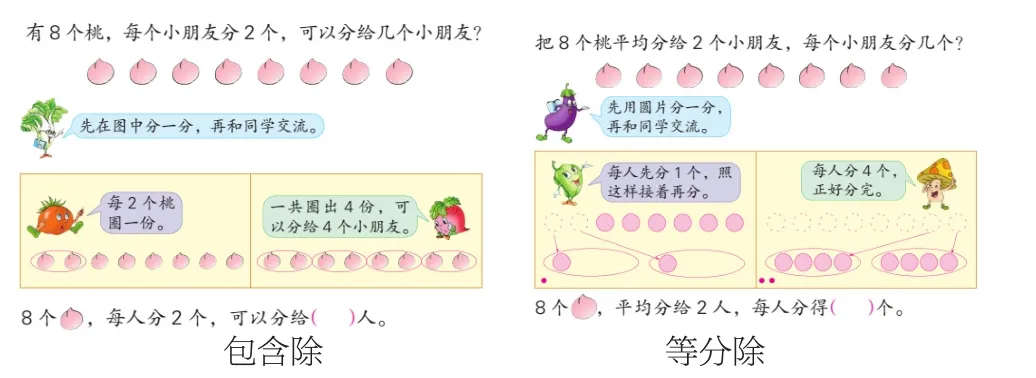
例如,苏教版二年级上册《表内除法》中有例2:8个桃,每个小朋友分2个,可以分给几个小朋友?是平均分中求“几份”的问题,是“包含除”,而例3:把8个桃平均分给2个小朋友,每个小朋友分几个?是平均分中求“每份的量”的问题,是“等分除”。理清除法算式的含义,能更好地提高学生的运算能力,同时为后续学习提供必要的支撑。
又如在学习分数时,它有“表示具体的量”和“分率”之分,恰恰就是“等分除”和“包含除”的模型。
通过整体构建知识框架,不仅让学生将阶段性知识完整建构,更将视野拓展至整个数的运算算理体系,还能帮助学生对其他方面知识融会贯通,帮助学生提高运算能力,更提升学生的数学素养。
运算能力的培养是培育学生核心素养的重要内容,作为教师,应“顺木之天以致其性”,在日常教学中顺应学生的基础,沟通知识的联系,引导探究新知,不断提升运算能力,提升核心素养。

