基于模型预测静态规划的自适应轨迹跟踪算法

王萌萌，张曙光

北京航空航天大学 交通科学与工程学院，北京 100083

轨迹跟踪需要飞行器对位置矢量等状态量按照预期方式实施跟踪。传统的方法多基于线性化模型进行反馈控制[1-3]，但往往受限于模型本身的非线性与状态间耦合程度。受到关注的方法还有反馈线性化[4-6]等其他方法，然而反馈线性化方法也受限于动态逆的对合条件与零动力学[7]。因而，自抗扰控制器在轨迹跟踪领域得到广泛关注[8-9]。基于最优控制方法的模型预测控制近年来被广泛应用于轨迹跟踪问题，例如文献[10-11]提出了一种使用非线性模型预测控制的无人固定翼飞行器轨迹跟踪算法。根据不同研究对象模型的复杂与非线性程度，模型预测控制要求一定的计算能力。

在各类基于模型解算生成指令的控制方法中，模型预测静态规划(Model Predictive Static Programming，MPSP)是由Padhi提出的基于模型的、解决一类带有终端约束的最优控制问题的高效算法[12]。其从原理上结合了模型预测控制与近似动态规划的特点，目前已有许多学者进行了扩展与应用[13-15]。MPSP算法最显著的特点的是其通过引入一个静态拉格朗日算子，将问题转换为一个静态优化问题，得出解析的关于终端误差的控制量修正量，这一特点使得MPSP算法具有较高的计算效率，具备在线应用潜力。Kumar和Padhi文献[16]中进一步提出了MPSP算法的一种扩展应用，引入了过程状态约束应用于轨迹跟踪问题，被称为跟踪模型预测静态规划(Tracking Model Predictive Static Programming，T-MPSP)。文献[17]中将T-MPSP应用于无人机自主着陆制导。作为MPSP算法的一种扩展应用，T-MPSP同样继承了MPSP算法的高效性与基于模型的特性。与传统的模型预测控制(Model Predictive Control，MPC)[18]相比，MPSP及T-MPSP中不存在数值优化的过程，直接给出了解析解，因此在实时性方面有着显著优势。

同时，T-MPSP对模型精度有明显依赖性。在一些特殊情况下，飞行器的实际情况与算法中使用的标称模型可能存在较大偏差。例如，当飞行器受损时，气动性能可能发生退化使得气动参数偏离标称参数。文献[19]中指出了当固定翼飞机机翼受损时的气动参数变化问题。其他模型扰动也广泛存在，例如飞行器质量等不确定性[20]。这也就意味着，基于模型的T-MPSP算法可能无法保证实际模型偏差下的跟踪效果。

针对上述问题本文进行了改进，引入参数估计思想抑制模型偏离影响。提出一种基于MPSP离散时间框架下的参数估计方法，将该参数估计方法与T-MPSP相结合，得到一种自适应T-MPSP算法。

1 自适应轨迹跟踪算法

为了提高对模型偏差的适应性，本文首先对标称模型的实际偏离进行在线参数估计，并将模型修正引入到跟踪环节中。因而，提出的自适应轨迹跟踪算法由2部分组成，分别是基于MPSP的参数估计与T-MPSP轨迹跟踪。2部分均使用显含待估参数的随时间推进离散系统动力学方程：

xk+1=Fk(xk,uk,νk)

(1)

式中：x∈Rn为状态矢量；u∈Rm为控制矢量；ν∈Rp为参数矢量；k=1,2,…,N-1，其中N为一个离散时间区间中的最终步。为了区分参数估计部分与轨迹跟踪部分的时间区间，分别以Ne与Nt标记相应的离散化步数，下标e对应参数估计，下标t对应轨迹跟踪。

1.1 基于MPSP的参数估计方法

根据本文所建立的控制思想，给出在MPSP框架下的参数估计算法。MPSP算法框架考虑一个过去的时间区间，对应的离散后的时间节点为k=1,2,…,Ne-1。为了更新当前参数，选择xNe作为当前时刻的状态量。考虑到如下输出方程：

(2)

式中：ye∈Rqe为参数估计中考虑的输出向量。定义当前时刻输出向量测量值与预测值之间的预测误差为

(3)

(4)

对式(1)进行泰勒展开，并考虑到小量近似，可以得到k+1 节点处的误差表示为

(5)

由于参数估计算法所考虑的时间节点均为过去的时间节点，控制矢量已知且确定，所以不考虑控制量的变化，即duk=0，式(5)可简化为

(6)

同理在当前时刻节点，即Ne节点有

(7)

代入式(4)后,可得

(8)

将式(6)中的dxk(k=1,2,…,Ne-1)不断代入可得

(9)

式中：

(10)

(11)

认为初始状态不变，则dx1=0，可以化简得到

(12)

(13)

式中：上标0表示计算过程中的中间变量。为了构建一个完整的最优控制问题结构，选取如下目标函数：

(14)

(15)

式中：λ为静态拉格朗日算子，通过静态优化理论求解取得最优解时的必要条件，并假设dν在各步均相等，可以得到

(16)

(17)

通过式(16)与式(17)求解参数修正量dν可得

(18)

式中：

(19)

由此，给出参数的估计值为

v=νp+dν

(20)

式中：ν为更新后的参数值；νp为更新前的参数值。值得注意的是尽管在推导过程中做出了参数在估计区间内时不变的假设，但是由于算法本身的快速更新特性，可以对时变参数进行估计。由式(12)中关系可得，补偿了参数修正量dν后，相应的系统预测输出误差也得到了补偿。从而在1.2节轨迹跟踪算法应用中，可以保证更好的跟踪效果。

1.2 跟踪模型预测静态规划

在1.1节得到模型修正量的基础上，本节将模型修正引入跟踪控制中。根据T-MPSP算法理论[16]，输出方程为

yk=h(xk)

(21)

类似1.1节推导式(5)的数学过程，不考虑参数变化，即dvk=0，可得

(22)

注意到，经过式(20)的修正后，式(22)的系统动力学方程Fk(xk,uk,νk)已使用更新后的参数，实现了对T-MPSP算法仅应用带误差的模型参数的改进。

类似式(7)～式(11)推导，可以得到

(23)

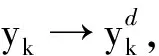
(24)

(25)

将式(25)代入式(24)中可得

(26)

考虑到小量近似，即Δyk≈dyk, Δuk≈duk，则

(27)

将式(23)代入(27,)可得

(28)

至此，目标函数被表示为了du的函数，于是通过最优控制理论可以得到一系列必要条件可以用于求解控制量的修正量，即du，如式(29)所示：

(29)

求解式(29)可以得到如下方程：

(30)

式中：最左侧系数矩阵对角线元素为Cij+Ri，其他元素为Cij。

其中：

i=1,2,…,Nt-1;j=1,2,…,Nt-1

求解式(30),可得到控制量的修正量为

(31)

于是更新后的控制量可以表示为

(32)

至此基于T-MPSP算法的控制量求解过程结束，注意由于T-MPSP算法多次使用了小量近似，所以可能需要迭代若干次才能满足轨迹跟踪的效果，仿真中一般在5次以内能收敛。此外，由于解算的结果均是显式的解析解，迭代所需的计算量较小，所用时间较理想。

如前述，本文将模型偏离参数引入动力学方程Fk(xk,uk,νk)中，扩展应用T-MPSP算法，建立自适应修正过程，从而保证了更好的轨迹跟踪效果。

2 仿真模型

飞行器质点模型为[21]

(33)

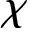
(34)

式中：ρ、S和C分别为大气密度、参考面积与气动力系数。对于轨迹问题，假定指令操纵响应具有一阶延迟，即

(35)

模型状态矢量与控制矢量为

(36)

通过欧拉法离散模型后得到的系统动力学方程为

(37)

式中：h为离散时间步长。

根据第1节，存在两组系统的输出矢量分别用于参数估计与轨迹跟踪：

(38)

(39)

3 参数估计与轨迹跟踪仿真分析

为验证自适应T-MPSP算法的有效性，应用参考文献[16]中的原始T-MPSP与本文提出的自适应T-MPSP在相同的飞行状态下执行相同的轨迹跟踪任务。飞行器的参数在表1中给出。选定待估计参数矢量为

以模拟出现损伤的情况，假定损伤发生于时t=15 s，且导致的参数偏差为ΔCLα=-0.5, Δm=-500 kg，并且考虑到测量噪声，测量方程为

式中：σ为测量的白噪音，白噪音的幅值为纵向位移、横侧位移、高度均为3 m，航迹偏角、航迹倾角均为0.1°，速度为1 m/s。根据CLα和m的数值大小比例，选定

(40)

同样根据状态量数值大小，选取Qk为以[0.3 0.3 0.3 10 10 1]为元素的对角阵。此外，选定Rk为

(41)

如此选择的原因在于希望使得控制量在一个预测周期前段修正较小避免突变。离散步长为0.2 s。Ne与Nt均为76，对应预测周期为75个时间节点，共计15 s。

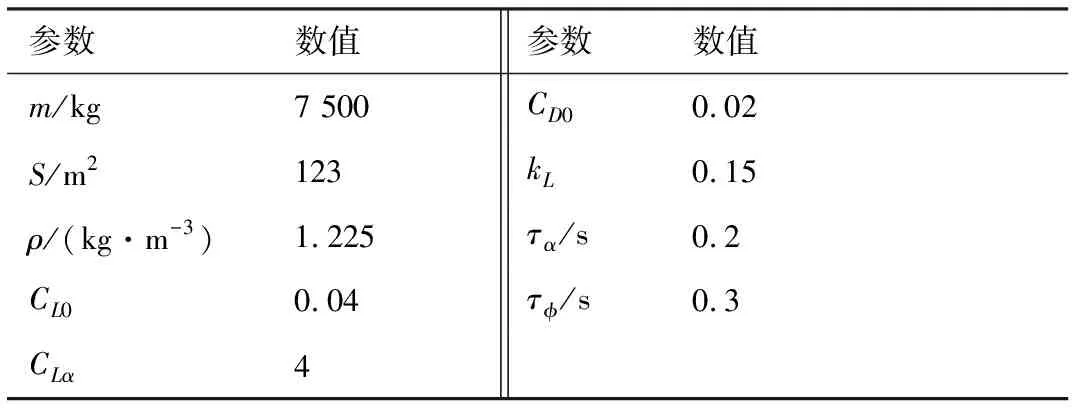
表1 飞行器标称参数Table 1 Nominal parameters in simulation test

参考文献[16]中T-MPSP与本文提出的自适应T-MPSP在相同的飞行器参数下执行圆周盘旋上升轨迹跟踪任务的结果对比如图 1所示。可以看出，改进后的自适应T-MPSP跟踪参考轨迹的效果显著好于T-MPSP算法，实际飞行轨迹与参考轨迹接近，而T-MPSP算法生成的轨迹则与参考轨迹有一定偏差。自适应T-MPSP中参数估计过程的结果如图 2所示，一个周期后，参数值得到了较为准确的估计。由于T-MPSP仅使用标称模型，没有进行参数估计，因此，图 2 中用于比较的变量为受损参数的真实值与自适应T-MPSP算法得出的估计值。

图3进一步给出参考文献[16]中的原始T-MPSP和本文自适应T-MPSP的航迹偏角、航迹倾角与速度曲线对比，可见，两种跟踪效果的差别更加明显。由于预测模型中存在参数误差，T-MPSP无法跟踪参考轨迹参数，其状态量在参考值附近振荡。相反，自适应T-MPSP算法由于及时修正了模型中的参数误差，实现了较好的跟踪效果。

迎角指令、滚转角指令与推力等轨迹控制量变化见图 4。与较快变化的状态量(轨迹角、速度)体现出相同的现象，T-MPSP给出的控制指令不断振荡，自适应T-MPSP在修正了由参数变化带来的误差之后，仅体现由测量误差引起的每一个制导周期的小幅修正。

从仿真结果中可以看出，本文提出的自适应T-MPSP算法实现了对参数的较准确估计，同时由于对模型参数进行及时修正，所生成的控制指令能实现更好的轨迹跟踪效果。且本文提供的自适应T-MPSP具备与MPSP/T-MPSP算法相似的收敛特性，迭代次数相当。

表2 中给出了自适应T-MPSP，包括参数估计与轨迹跟踪的计算耗时。共进行轨迹跟踪任务(飞行器圆周盘旋上升)仿真测试100次，仿真均在Windows10(i7-6700，16 G内存)的MATLAB R2016b环境下完成。每次仿真模拟飞行150 s，共测试10个周期，每个周期计算耗时1.5～2 s。由表2得出，该算法平均计算耗时短，而实际飞行时，机载计算采用的是运行速度快得多的计算系统(计算速度至少快1个数量级)。从而表明提供了解析解的自适应T-MPSP具有实时应用潜力。

表2 参数估计与轨迹跟踪耗时Table 2 Time consumption of estimation and tracking

4 结 论

1) 在离散模型预测静态规划(MPSP)框架下建立了一种高效的实时参数估计算法，可有效准确估计偏离标称模型的参数。由于使用当前时刻的测量值，保证了参数能够不断地在线更新，从而对于时变参数也能进行较好的估计。

2) 提出的结合参数估计的自适应跟踪模型预测静态规划算法，相较T-MPSP算法，能通过模型参数更新，更好保证轨迹跟踪的效果，同时能避免误差的积累导致算法发散。

3) 算法的参数估计与轨迹跟踪两个部分，均是在模型预测静态规划的基本框架下扩展，其解析解特性保证了较高的计算效率。