地质灾害流固耦合模型研究

丁靖洋

（北京市地质工程勘察院，北京 100048）

0 前言

我国是地质灾害较为频发的国家之一，改革开放以来，随着大规模基础设施的建设，地质灾害也进入频发期，且治理费用高昂，动辄几千万至上亿元（王贡先，2004；王贡先，2005；黄润秋，2007），而其中降雨是地质灾害发生的最重要诱因之一（刘艳辉等，2011）。铁路交通因其具有线性工程的特点，沿途一旦发生地质灾害，将会对其运营造成严重威胁，因此针对线性交通工程进行地质安全监测、预警具有十分重要的意义。

“京张铁路（居庸关隧道进口段）地质安全监测示范工程”是“京津冀协同发展交通网络地质安全监测预警系统”建设的重要组成部分，旨在对“京张客专”沿途的地质环境进行监测预警，并进一步为构建完整的京津冀交通网络地质安全监测预警系统提供经验和技术支持。

“京张铁路（居庸关隧道进口段）地质安全监测示范工程”的研究思路是：（1）在“京张客专”沿线选择一处突发性地质灾害较发育的试验区域；（2）在试验区域内布设一系列监测设备，为地质安全风险评估提供依据；（3）通过勘探手段获得试验区域内地质信息，建立三维地质体展示模型；（4）开展室内土力学试验，获取力学、渗流等一系列参数；（5）构建流固耦合本构方程，对试验区域进行数值模拟研究，并与现场监测数据进行对比分析，验证方程及模拟结果的可靠性、合理性。

1 监测设备埋设

试验区位于“京张客专”居庸关隧道进口段，区内发育有一条“V”型冲沟，沟内含有大量物源体，在暴雨工况下极易发生泥石流、滑坡等地质灾害。

根据勘察资料，该试验区30m深度范围内的地层分为新近沉积层、一般第四纪沉积层、长城系高于庄组基岩。

现场埋设的监测设备有：全球导航卫星系统（Global Navigation Satellite System，GNSS）、阵列式位移计（Shape Accel Array，SAA）、精力水准、土压力计、孔隙水压力计、土壤水分传感器等。由于设备调试、数据接收等原因，本文数值模拟选用的现场监测数据为土壤含水率、地下水平位移。

（1）土壤水分传感器：现场布设2个土壤含水率测点，设备型号为CSF11型土壤水分传感器，如图1(a)所示。

（2）地下水平位移监测（SAA）：在试验区内布设1个地下水平位移监测点，SAA埋设总长为8m，如图1(b)所示。

2 流固耦合本构模型构建

基于有效应力原理（Terzaghi，1923）、非饱和渗流理论（Richards，1931）及Mohr-coulomb屈服准则，本文作者已推导获得了流固耦合本构方程（丁靖洋，2017），即：

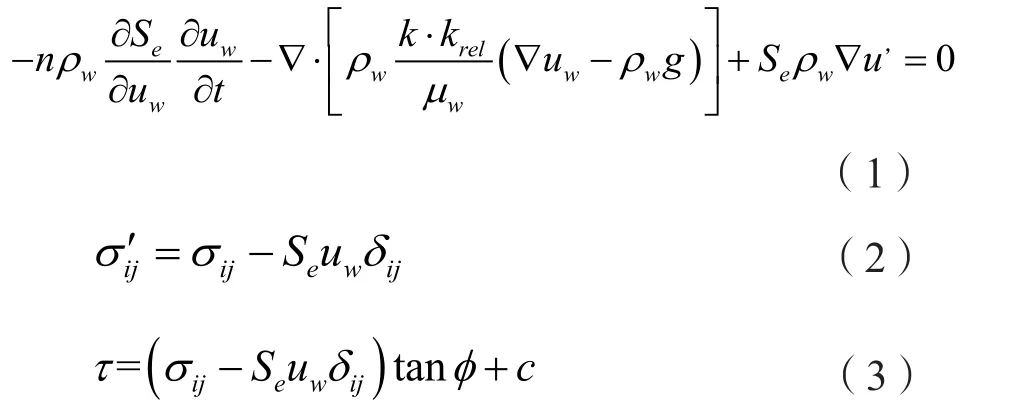
式（1）—式（3）中：n为孔隙介质孔隙率，ρw为流体密度，Se为流体相的有效饱和度，uw为孔隙水压力，k为固有渗透率，krel为非饱和到饱和过程中的相对渗透率，μw为流体粘性系数，u，为流体速度；为有效应力，σij为主应力，δij为克罗内克符号；τ为剪应力，ϕ为内摩擦角，c为粘聚力。

进一步，为了考虑土体变形对孔隙率的影响，由孔隙比与体积单元变形关系可知：

式中：e，v，vs，v0，vs0和e0分别为变形过程中的孔隙比、单元体积、单元固体体积、初始单元体积、初始单元固体体积和初始孔隙比。式（4）中，表示单元体积变化量，可用第一应变量表示为：

忽略单元变形过程中的固体介质变形，则有：

将式（5）、（6）带入式（4），得到：

则孔隙率与应变的关系为：

式（8）中：n0为孔隙介质的初始孔隙率，为第一应变量。

综合式（1）、（2）、（3）、（8），获得一种新的考虑孔隙率演化的非饱和渗流-应力耦合模型。

3 数值计算模型

3.1 三维离散模型

在现场勘察数据的基础上，借助于OpenGeoSys（OGS）软件及GMSH前处理软件，建立了试验区域的三维地质体模型（丁靖洋，2017），其中第一、二层土体的四面体单元尺寸为3m3，底层基岩单元尺寸为12m3，共计24498个（图2）。

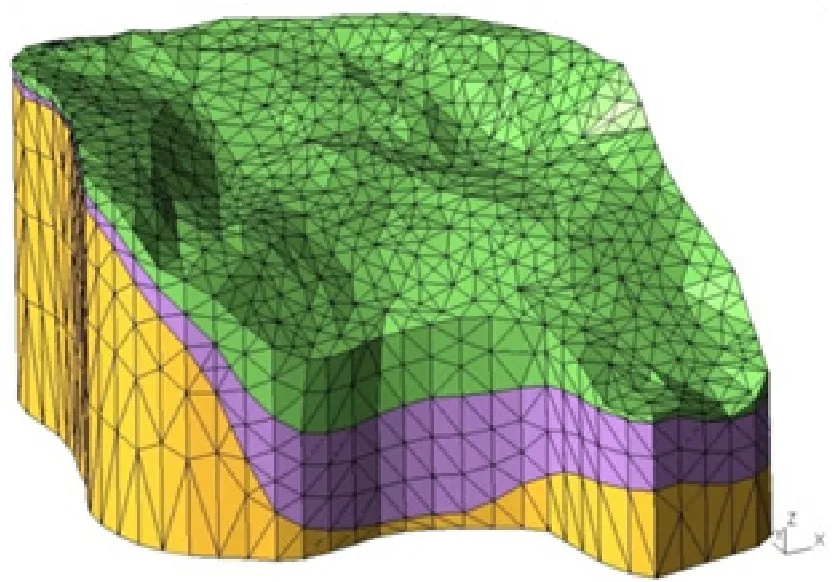
图2 单元网格模型Fig.2 Element of the model

3.2 数值计算模型参数

本次研究过程中，主要针对第一层和第二层土体的降雨入渗变形过程进行模拟，第三层地层为基岩，力学强度较高，渗透率较小，因此，数值计算中的关键地层为第一和第二层，第三层假设为线弹性属性。

数值模拟，流体设定为水，密度为1000kg/m3，动力粘性系数为0.001Pa·s。对试验区现场获得的土样进行室内土力学试验，确定模型中各地层的参数见表1。

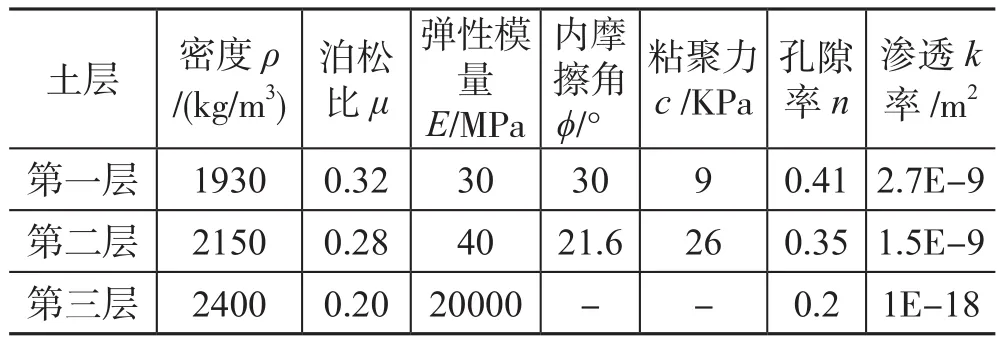
表1 各地层模拟参数Tab.1 Parameters for the numerical modeling

基于现场土样，通过试验测定了第一层和第二层土体的土水特征曲线（戚国庆等，2004）如图3所示：

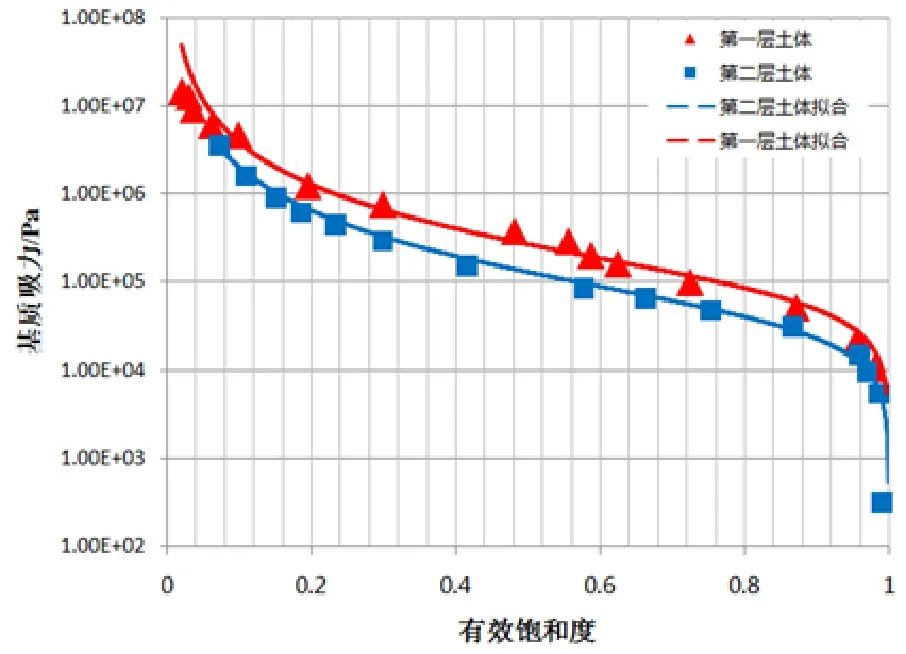
图3 土水特征曲线及拟合参数Fig.3 Water retention curve and fitting parameters

图3 中采用的拟合方程为Van Genuchten模型（Genuchten，1980；李少龙等，2006），即式（9）。计算获得的第一层土体的a=0.098，m=0.385，第二层土体的a=0.212，m=0.378。

3.3 初始条件及边界条件

根据地质勘查结果及图3中的参数，假定第三层基岩的含水率接近饱和，则设定第一层、第二层、第三层土体的初始饱和度分别为0.28、0.5、0.93。

图4所示为现场监测设备记录的2017年6月21日—6月26日，共计约120小时内的土壤含水率数据，经过换算，得到有效饱和度随时间的变化曲线。

数值计算中：设定模型四周为固定位移边界，并固定模型底部垂直方向的位移；基于图3拟合结果，将有效饱和度转化为等效基质吸力，作为模型上表面的入渗边界条件，以此模拟降雨入渗过程引起的地表含水率和吸力变化；模型其他表面设定为不入渗边界，在OGS软件中表示无流体流入及流出。

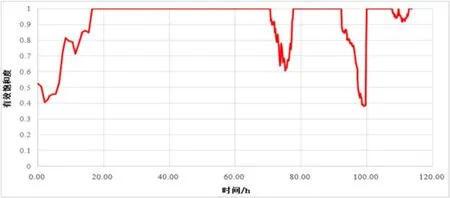
图4 地表有效饱和度随时间变化曲线Fig.4 Effective saturation curve with time

4 模拟结果

4.1 位移监测点模拟

现场布设有一个地下水平位移监测点（SAA），实时记录降雨过程中的测点位移变化情况；通过对数据进行筛选、分析，选取6月23日、24日两天持续降雨的监测数据。由于测点测定的位移主要发生在x和y两个方向，而z向位移基本可忽略不计，因此获得位移随SAA埋深的变化曲线如图5所示。

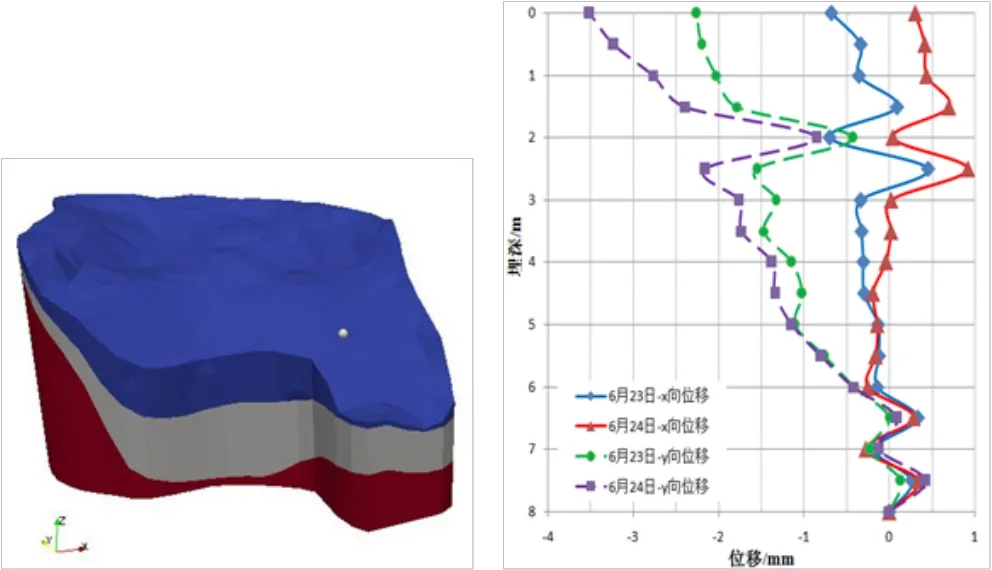
图5 现场监测点位置及x、y位移数据Fig.5 The location of SAA equipment and x/y-displacement data

数值模拟计算获得的该测点x、y向位移如图6所示。对比现场监测数据与数值模拟结果可知，该本构模型能够在一定程度上很好地反映实测结果。在SAA埋设处，地表位移较大，随着深度的增加，位移呈减小趋势；而数值计算结果能够很好反映位移随深度的变化规律，且对于潜层松散土体，即在不考虑构造因素、易形成地质灾害物源体的区域，基于非饱和渗流理论的模型计算结果能够较好地匹配降雨情况下的位移数据。

同时应该看到，由于OGS软件的运算基础是连续介质有限元理论，其对于介质的均匀性假设以及网格尺度造成的计算误差，造成了模拟结果与现场实测数据存在一定的差别。但整体上，本次数值计算能够有效反映降雨入渗过程引起的地层变形情况。

4.2 有效饱和度与位移模拟

本文分别模拟计算了20h、40h的位移及有效饱和度分布云图，如图7所示。由图4可知，20h以内，土壤含水率监测位置处未达到饱和状态；在20～40h，测点处持续呈饱和状态。由图7(b)可知，20h时模型左上部坡面最先达到饱和，且该处产生较大位移（图7(a)），这是由于该处第一、第二层土体较薄，渗透压力梯度较大，在渗透力驱动下孔隙水将逐渐向模型中部汇集；至40h，随着持续的降雨入渗，模型左上部出现大范围饱和区域，相对应的位移也在逐渐增大（图7(c)），发生地质灾害的风险增加。

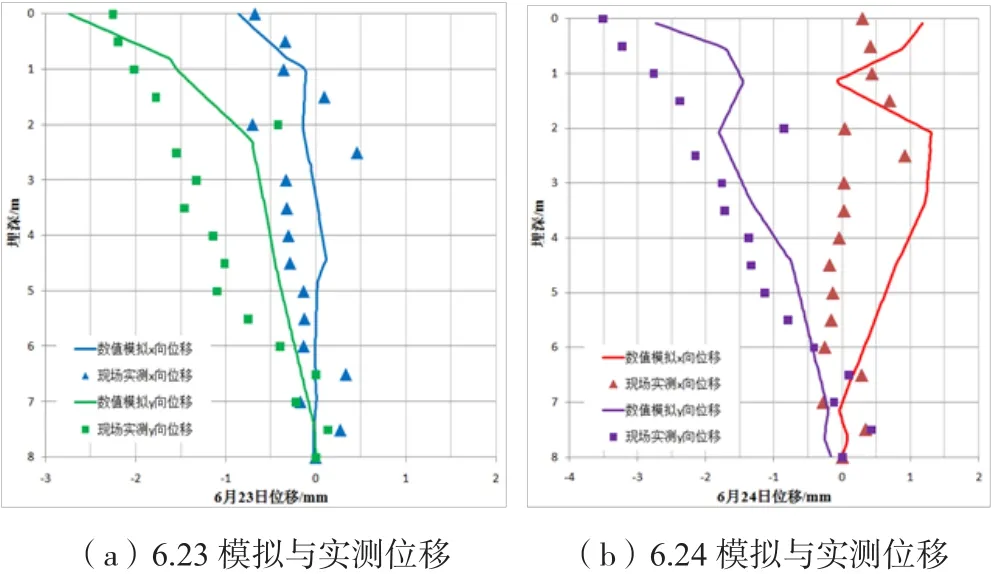
图6 现场监测与数值模拟位移数据Fig.6 Displacement data of monitoring and numerical calculation

上述现象表明，有效饱和度增大、基质吸力减小，是导致土体产生较大位移的重要原因：在降雨条件下，地层将被软化，尤其是在地层分界处，由于力学性质发生变化，极易产生软弱结构面；在渗流场-应力场的耦合作用下，孔隙水压力的变化导致了有效应力的改变，并最终导致滑坡、泥石流等地质灾害的发生。

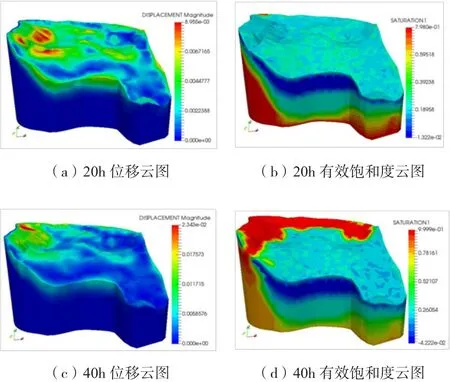
图7 位移及有效饱和度分布云图Fig.7 Contour plots of displacement and effective saturation(a) Displacement in 20h (b) Effective saturation in 20h (c)Displacement in 40h (d) Effective saturation in 40h

5 结论

本文依托于“京张铁路（居庸关隧道进口段）地质安全监测示范工程”，借助于OpenGeoSys（OGS）软件对试验区的降雨入渗过程（流固耦合）进行了数值模拟研究，并对现场监测设备采集到的数据进行了拟合分析，主要成果及结论为：

（1）推导获得了孔隙率随应变的演化方程，在有效应力原理、非饱和渗流理论、Mohr-coulomb屈服准则的基础上，建立了一种新的非饱和渗流-应力耦合模型；

（2）开展室内土力学试验，获得耦合模型所需力学、渗流参数；

（3）在现场采集到的土壤含水率数据的基础上，开展数值模拟研究，并将位移模拟结果与现场实测数据进行对比、拟合，计算结果表明该研究方法的可行性、合理性；

（4）降雨入渗过程，即有效饱和度逐渐增大、位移逐渐增加的过程，是地质灾害发生的重要诱因。