基于图论的消声器拓扑关系分析及子结构划分方法

张 杨， 邓兆祥， 温逸云

(重庆大学 机械传动国家重点实验室，重庆 400044)

加装排气消声器是降低汽车噪声最有效的手段，因此设计出与排气噪声相匹配的消声器意义重大[1]。消声器的设计大多根据发动机的噪声特性设计出若干消声子结构，再将这些子结构按照一定的顺序拼接在一起，形成最终的设计方案。而由于受到底盘布置空间的约束，这些子结构通常会采用多个子结构共用一个腔室的拼接方式，这种拼接方式可能会造成多个子结构内部的相互干扰，甚至使部分子结构之间的拓扑关系发生重构，从而对消声器的声学性能产生较大影响。但现阶段的国内外研究大多集中在消声结构设计及参数灵敏度分析[2-5]和消声器性能分析方法[6-9]，而针对消声子结构拼接后的拓扑关系变化及其对消声器声学性能影响的研究尚未见报道。

本文首先利用实验方法验证了消声器声学有限元分析的准确性；然后利用有限元方法分析了子结构拼接方式对消声器整体性能的影响，并从拓扑关系角度解释了该影响的成因；然后，在总结子结构拓扑关系的基础上，基于图论的相关方法提出了一种可以判断消声器内部连接关系的拓扑图，并根据不同类型子结构的图形特征得出了消声器子结构划分的具体方法；最后，通过实例验证了该方法的工程适用性。

1 消声器声学有限元分析与试验验证

本文设计了如图1所示的消声结构，其设计初衷由三个子结构组成：①管1、孔1、管1′及腔1组成的穿孔管子结构；②管2、孔2、管2′及腔1组成的穿孔管子结构；③管1′、管2′及腔2组成的插入管子结构。

由于截面对本文研究的拼接拓扑关系没有影响，本文将截面固定为125 mm×250 mm的矩形，样件的其他尺寸参数为：L1=305 mm，L2=150 mm，a1=b1=250 mm，a2=b2=150 mm，la=lb=5 mm，S1=S2=45 mm。

消声器的传声损失定义为进出口处的声功率级之差，它表征消声器的固有特性，与声源无关[10]，因此本文以传声损失作为评价消声器声学性能的指标。消声器传声损失试验利用B&K的声学测试系统，包括PULSE3560B采集前端、2716C功率放大器、4260T阻抗管和4187型1/4英寸传声器等，构建的传声损失测量装置如图2所示，试验方法及数据处理参照文献[11]，试验室温为16.5 ℃。消声器传声损失数值仿真采用LMS Virtual.Lab建立有限元模型，进口边界条件为单位振速，出口设置为全吸声，仿真温度和测点位置均与试验相同。

图1 样件示意图Fig.1 Schematic diagram of sample

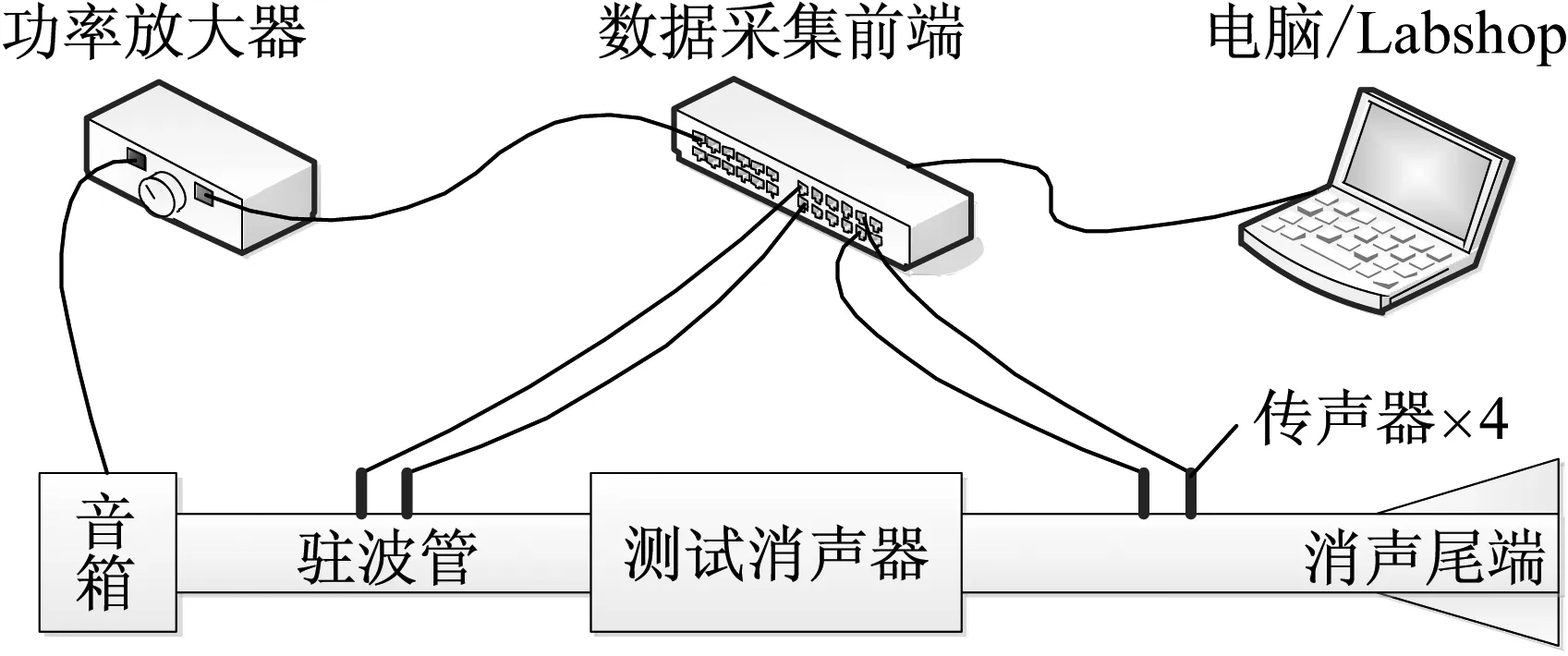
图2 消声器传递损失测试示意图Fig.2 Sketch of muffler STL measurement

首先，对图1中样件的传声损失进行有限元仿真和试验测试，其结果如图3所示。图中，实线为仿真结果，点线为试验结果，对比两条曲线可以看出有限元仿真与试验结果基本一致。在验证了有限元仿真方法的正确性的基础上，再使用有限元法对相同子结构不同拼接方式的仿真结果进行对比。比对模型采用了图1样件中所包含的三个结构直接串联(即两个穿孔段不再共用同一腔体)的形式，其传递损失仿真结果如下图虚线所示。对比两次仿真结果不难发现不同拼接形式对消声性能的影响较为明显，也表明本文的研究具有较强的工程实用价值。

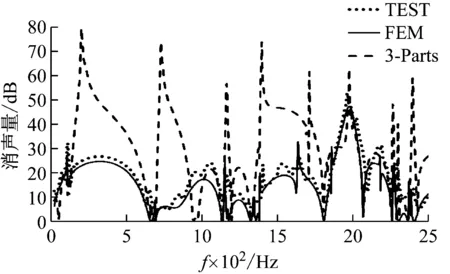
图3 试验仿真结果对比Fig.3 Comparison of test and simulation results

2 成因分析与理论解释

为了分析拼接形式对消声性能造成影响的原因，本文将样件消声器分成如图4所示的两部分，分别进行有限元仿真，并与整体消声器的仿真结果对比。其相关尺寸为：L1=305 mm，L2=150 mm，a1=b1=110 mm，a2=b2=110 mm，la=lb=85 mm，S1=S2=45 mm。

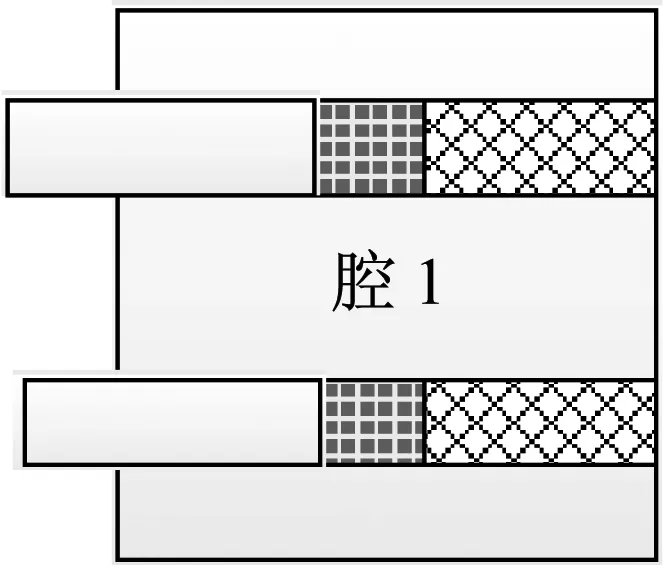
图4 分腔子结构Fig.4 Schematic diagram of sub-structure by chamber

从如图5所示的仿真结果中可以看出：左边第一腔结构的传声损失曲线和整个消声器的传声损失曲线趋势十分相似，只是在某些峰值位置存在一定差距；同时右边第二腔结构的传声损失曲线则和整个消声器的传声损失曲线差距较大，也未能提供整个消声器的传声损失曲线具有而左边第一腔结构传声损失曲线不具有的峰值。

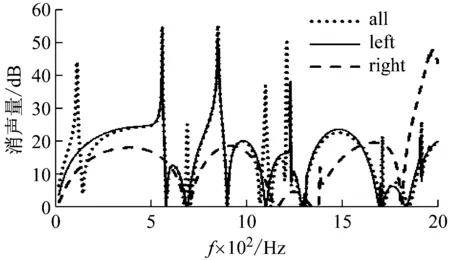
图5 分腔仿真结果Fig.5 Simulation results of sub-structures by chamber

为了分析整体消声器传声损失中特有消声峰值的成因，本文查看整体消声器模型115 Hz处的声压云图(如图6所示)，可以明显发现右边第二腔发生了共振作用，而管1′和管2′则充当了共振腔喉管的作用。

为了验证这一结论，本文将消声器第二腔的长度L2增长到190 mm再对比原结构的传声损失进行对比。如图7所示。

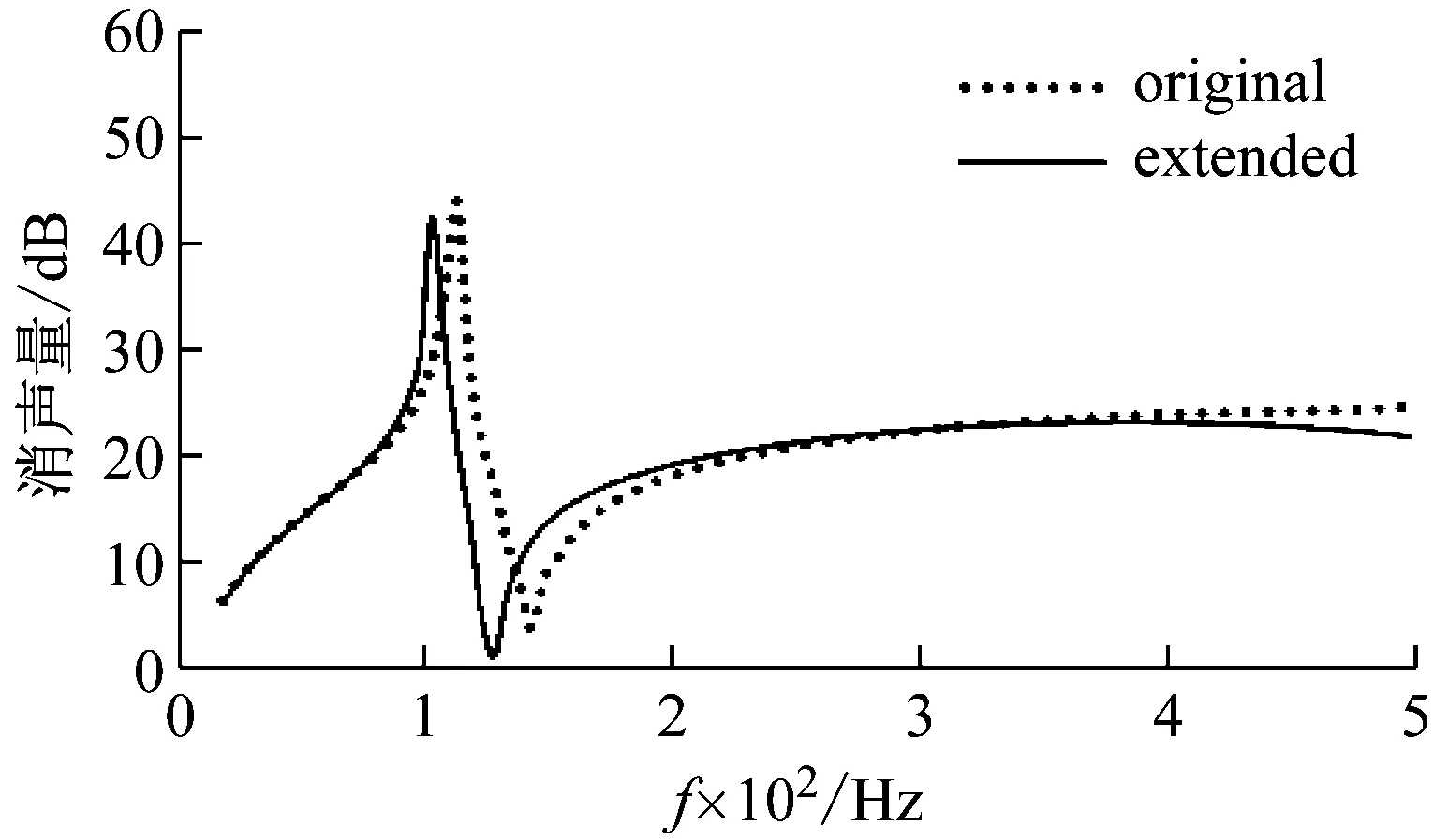
图7 模型峰值对比Fig.7 Comparison of model peak values

可以发现，其共振峰值随着共振腔体积的增大向低频偏移。这与共振腔消声原理[12]一致：旁支管的声质量为

M=lρ0/S

(1)

共振腔的声容为

(2)

系统一阶固有频率为

(3)

整理得

(4)

l的修正公式为

l=l+0.85d

(5)

式中:l为旁支管长度；S为旁支管总横截面积；V为共振腔体积；ρ0为空气密度；c0为空气中声速；d为旁支管横截面直径。当入射声波频率f=f0时将形成共振，从而产生消声的作用。应用上述公式的计算的理论值与仿真计算值的误差较小。理论仿真峰值对比值,见表1。

表1 理论仿真峰值对比Tab.1 Comparison of theoretical and simulation peak values

综合上述分析说明：样件消声器中管1′、管2′以及腔2发挥了旁支共振腔作用，而剩余的部件则形成恒流式插入管子结构，这与两个穿孔管子结构和一个插入管子结构组合的设计初衷大相径庭。因此样件消声器在115 Hz等出处出现了子结构设计阶段并未设计的消声峰值，同时也无法发挥三个子结构直接串联时穿孔管子结构产生的共振峰等特征。这也解释了图3中，三个子结构直接串联结构与实验结果相差较大的根本原因。深入对比两种拼接方式的不同之处，可以发现造成子结构重构的原因是：子结构拼接时，所设计的两个穿孔管子结构采用了共用腔体的拼接方式，使得管1′和管2′都同时连接腔1和腔2，成了并联的形式。从而重构形成了由管1′、管2′和腔2组成的共振结构。

由此可见，子结构不同拼接方式对消声器整体性能产生影响的主要原因是：某些拼接方式会造成子结构间的拓扑关系产生干扰，从而发生子结构的重构，造成所设计的子结构性能失效。如果能够有效识别子结构间的拓扑关系及子结构的重构，则可以在子结构拼接时有效避免子结构性能失效问题；而正确划分子结构并认知所划分子结构所发挥的功能，也是消声器结构改进和参数优化的重要前提。

3 消声器内部结构拓扑图

经过拼接后的消声器内部结构通常较为复杂，并不能直观的分析出其内部部件的拓扑关系。而图论是一种用图形来描述某些事物之间某种特定关系的数学方法[13]，因此本文引入图论的数学方法，将消声结构内部复杂的连接关系转化为明确的图线，从而更为准确直观的反映处消声器内部的拓扑关系。图论中所谓的“图”是指事物及事物之间的关系都可以抽象成点与点之间连线组成的图形。图一般用G表示，这些点称为图G的节点(用V表示)；这些点间连线称为图G的边(用E表示),一个图是由点集V和边集E所构成的二元组，记为G=(V,E)。如果图G的任意两个顶点之间至少有一条边相连，则称图G是“连通图”[14]。

要将图论应用到消声器子结构拓扑关系的分析中，必须首先明确如何完成子结构的几何抽象，即确定拓扑连通图中点集V与边集E所代表的部件或连接方式。通过对众多消声器案例内部结构的总结归纳，本文将腔、管、管套等部件作为点集V，将管开口端，管孔、板孔作为边集E，用来表征消声器部件(点集V)之间的连接关系。特别指出的是穿孔管中由于穿孔的存在，将管的连接关系分为入口、穿孔和出口三种，为了更准确地表达这个三种连接方式之间的关系，需要将原本一根整体管从穿孔位置分为2段处理(如图8所示)。而考虑到支路上并联结构的存在，本文选取了图论中的“无向连通图”(即边集E中的任意一条边都没有方向性)。同时本文在点集V中增加了整个消声器的进出口节点，以便更为明确的区分出主通路和支路。

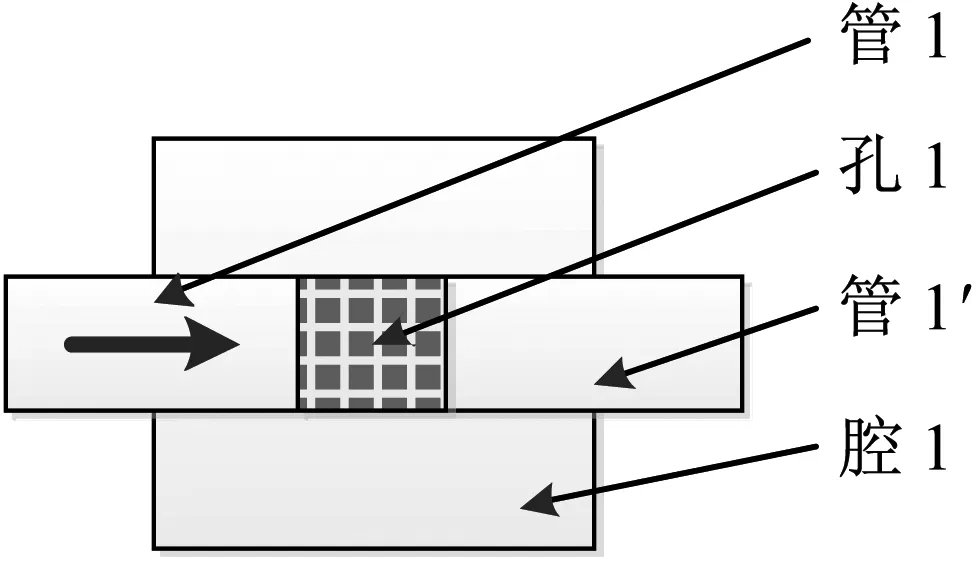
图8 穿孔管拓扑图Fig.8 Topological graph of perforated tube

基于该方法，本文中的样件可以表达为如图9所示的拓扑图，此图可以明确的反映出消声器内部部件的拓扑关系。其中管1与管2分别为消声器的进出口，管1与管2在连接腔1的同时，又分别通过管1′和管2′与腔2相连。可以直观的看出腔1和腔2组成了并联的形式，而并非是子结构串联形式，这也是图3中两种拼接方式的仿真结果差距较大的原因。

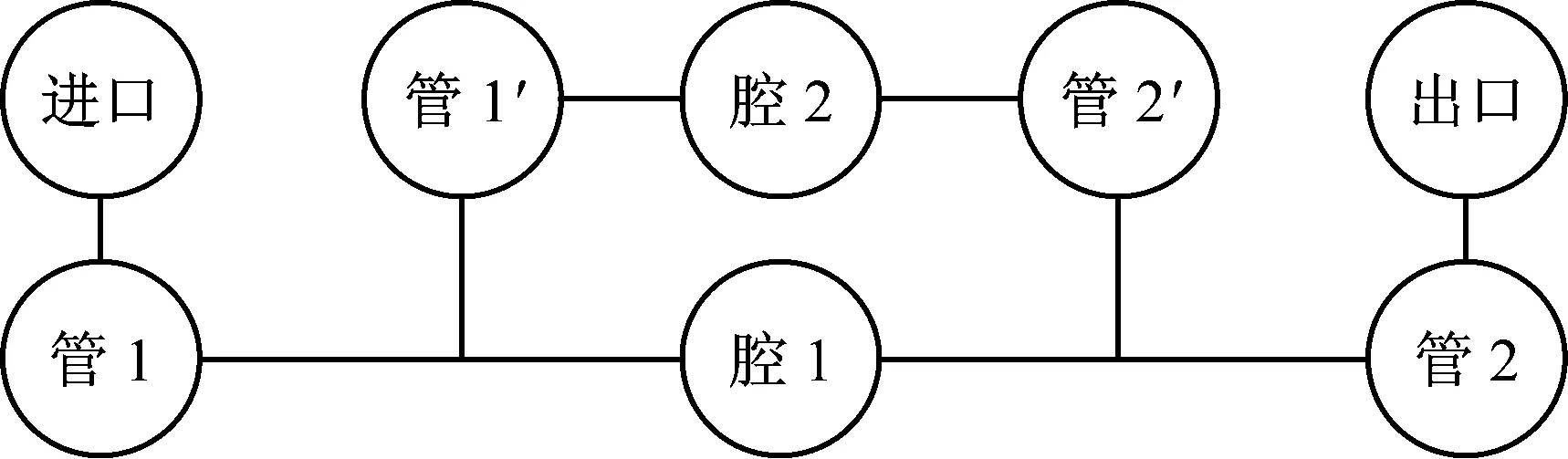
图9 样件拓扑图Fig.9 Topological graph of sample

4 消声器子结构划分方法

在了解消声器内部拓扑关系的基础上，如何正确的划分子结构单元并判断子结构单元所发挥的作用，是把握消声器实际性能的重要前提。从设计角度来看，其实质就是查看子结构拼接之后子结构所发挥的功能是否与设计初衷相一致。除阻性结构外，消声器中的功能腔主要分为扩张式和共振式两种形式，确定这两种功能腔拓扑关系的特点及其在拓扑图中的具体表现形式是消声器子结构划分的重要依据。

广义的扩张式结构通常需要一个让声音扩散的腔体空间，且进出通道与腔体空间是串联在的消声器的主通路之中的。而共振式结构则需要一个相对封闭的旁支结构(并不串联在消声器的主通路之中)，才能使腔体中的流体在受到压力作用时产生类似“弹簧”的反作用力以产生共振(其原理如图10所示)，且与该腔体通过一个或多个喉管与主通路的某区域连接。

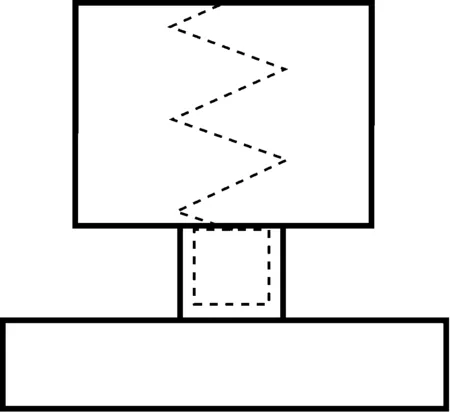
图10 共振式结构等效模型Fig.10 Equivalent model of resonant structure

因此在利用消声器内部结构拓扑图确定各子结构的连接关系后：根据共振结构都要求有一个旁支的封闭区域(进出口相同或进出口连接相同区域)，找到旁支通路上只与主通路固定区域连接的腔体，则该腔体必然发挥共振结构的作用，且该腔体与主通路连接的部件即发挥共振结构的喉管作用；由于共振结构仅对共振频率附近的噪声具有消声作用，对其它频率的消声量影响并不大，因此可以在识别共振结构后将其所在支路直接除去，而并不会对剩余结构的声学性能产生较大影响。同时考虑到扩张腔的进出通道与腔体空间是与主通路串联的，所以在除去所有的共振支路后，主通路上的各腔体可以按照从进口到出口的先后顺序逐步串联为新的子结构。

图9中可以看出，管1′和管2′与腔2形成相对封闭的分支结构，只通过管1′和管2′直接与腔1连通，符合共振结构的判断；而除去共振支路后的部分则连接为新的子结构，即图4中的Left模型。而图5中除了个别共振峰之外，Left模型和整个消声器的传声损失曲线较为接近，也证明了该划分方法的合理性。

综上所述，基于图论的消声器内部结构拓扑关系分析以及消声器子结构划分的具体方法可以归纳为以下4个步骤：

步骤1 绘制节点部件,包括腔、管以及管套；

步骤2 绘制部件间的连接线,包括管端面，以及管孔和板孔；

步骤3 共振子结构划分,如果某腔是拓扑图中某一支路上唯一的腔体，且该支路只通过有限个连线与主通路上的同一部件连接，则该支路为共振子结构；

步骤4 其他子结构划分,除去所有共振支路后，主通路上的各腔体则按照从进口到出口先后顺序串联为新的子结构。

利用该方法可以正确分析出子结构拼接后消声器内部的拓扑关系，并准确的完成消声器子结构的划分。此方法可以帮助设计者有效的了解各子结构在消声器中所发挥的功能作用以及子结构尺寸参数对消声器整体性能的影响机制，从而提高消声器的设计效率；同时准确把握消声器拼接后的声学性能，可以有效防止拓扑关系变化造成的子结构功能失效，避免设计失败。

5 案例应用

为了验证基于图论的拓扑关系分析及子结构划分方法的工程适用性，本文选取了如图11和图12所示的消声器结构进行验证。从两个示例的拓扑图可以看出图11和12中的主通路与旁支结构均可有效识别。

根据子结构划分规则，可以看出图11中的腔2独自出现在支路上且仅通过孔1与主通路相连，因此腔2被判定为共振式子结构，除去腔2所在的支路后，腔1与腔3分别于相连的管道组成扩张式子结构。这与实际消声器由两个插入管式子结构和一个穿孔管子结构组成的基本事实完全一致。由此可见，本文提出的子结构划分方法可以正确识别子结构直接串联的消声器。

图11 分析示例一Fig.11 Analysis example 1

图12 分析示例二Fig.12 Analysis example 2

图12中的腔2位于拓扑图的支路上，并仅通过管2、管3与腔1连接，因此腔2为共振式子结构，管2与管3发挥了喉管的作用。剩下的管1、腔1和管4组成扩张式子结构，其中管1为进口，管4为出口。

为了验证子结构划分的正确性，本文利用有限元方法对所划分的子结构与消声器整体分别进行有限元仿真分析(其详细尺寸参数如图13所示)，其传声损失结果的对比图如图14所示。可以看出，消声器整体仿真结果基本发挥了子结构的性能特征，也说明子结构划分结果正确。由此可见，本文提出的子结构划分方法可以正确识别子结构并联的消声器。

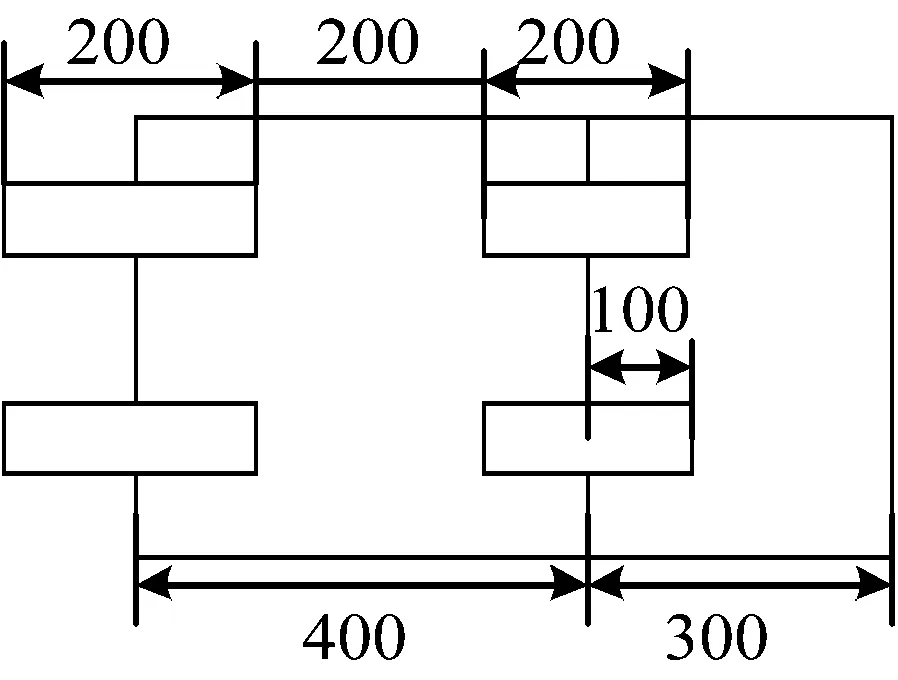
图13 示例二尺寸参数Fig.13 Parameters of analysis example 2

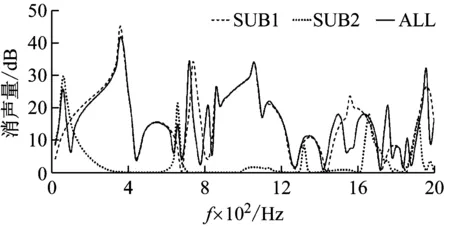
图14 子结构与消声器整体仿真结果Fig.14 Simulation results of sub-structures and whole muffle

6 结 论

(1)子结构的拼接方式对消声器整体性能有影响，甚至可能造成子结构性能失效。该影响的主要成因是拼接后消声器内部拓扑关系发生变化形成了新的子结构。

(2)基于图论的相关理论，提出了一种以腔、管、管套为节点，管端面、管孔、板孔为连接线的消声器内部拓扑关系图。该拓扑图可以比模型剖面图更加准确直观的反应出消声器内部结构之间的拓扑关系。

(3)基于扩张式与共振式消声单元的消声原理，分别归纳出其在消声器结构拓扑图中的特征，并提出了子结构划分方法：如果某腔是拓扑图中某一支路上唯一的腔体，且该支路只通过有限个连线与主通路上的同一部件连接，则该腔体及其有限个连接将组成共振子结构；除去所有共振支路后，主通路上的各腔体则按照从进口到出口先后顺序串联为新的子结构。该方法可以根据子结构的实际功能完成子结构的准确划分，对指导消声器设计和改进具有工程实用价值。