多频激励下添加线性振子磁悬浮能量采集系统建模及其输出功率影响参数分析
王祖尧, 丁 虎, 陈立群,3
(1.浙江科技学院 理学院,杭州 310023;2.上海大学 上海市应用数学和力学研究所,上海 200072;3.上海大学 力学系,上海 200444)
近年来,国内外研究人员对振动能量采集进行了大量的研究[1-7],力图提高振动能量采集的效率和扩大采集的频率范围。而大多数研究的是单频外部激励条件下的振动状态。在实际环境中,外部激励大多为复杂的多频激励。比如系统处在两个激励源中,或者行走机械在工作时,路面给系统的激励与机械本身的动力系统产生的激励形成多频激励。多频激励容易产生混沌行为,而往往会导致系统振荡或不规则运动。因此,需要研究多频激励对系统的影响。目前,已有许多学者对多频激励下的系统进行了研究。毕勤胜等[8]利用Flouquet理论和解通过转迁集时的特性,研究了多频激励Duffing方程一次近似解的各种分岔模式及其转迁集。Yang等[9-10]利用多尺度法研究了一类Duffing-Van der Pol耦合非线性系统的响应。杨德森等[11]利用多尺度法对硬弹簧特性Duffing系统的幅频响应进行分析可知,多频激励改变了单频激励条件下系统的主共振状态,使单频激励条件下的曲线产生了偏移。Zhou等[12]利用分析法和数值仿真研究了Duffing-Van der Pol振子在外激励和参数激励下的混沌运动,提出了可控制频率的新的动力学现象。
虽已有众多研究者对多频激励作用下动力学行为进行了研究,但关于多频激励作用下多自由度系统的能量采集还很少涉及。本文在文献[13]基础上研究了在增加了一个线性弹簧振子后,磁悬浮磁电能量采集系统在多频激励下的动力响应。通过受力分析建立电力耦合的非线性振动方程组,利用谐波平衡法和弧长法得到该系统在外部多频激励作用下的稳态平均功率的幅频响应,并对比不同参数下系统的响应,研究系统的参数对能量采集的影响,还通过直接数值方法验证解析结果。
1 磁悬浮非线性能量采集系统建模
本文研究一种新型磁悬浮能量采集器,这种磁悬浮采集系统原理示意图如图1所示。磁悬浮采集装置是在四根对称放置的直柱上下两端各固定一个磁体,在两个永磁体之间放置一个可以上下移动的悬浮磁体,通过四根对称放置的直柱来控制它的水平方向运动。中间的磁体的磁极需要与上下两个磁体的磁极相反,以产生相互间的排斥力,并在四根对称放置的直柱外侧上部和下部绕有铜线圈。当收到外界的多频激励时,引起中间永磁体的上下运动,在铜线圈内产生感应电动势。根据文献[14],可以得出图2中间磁极受到磁力的总和表示为k1x+k3x3。
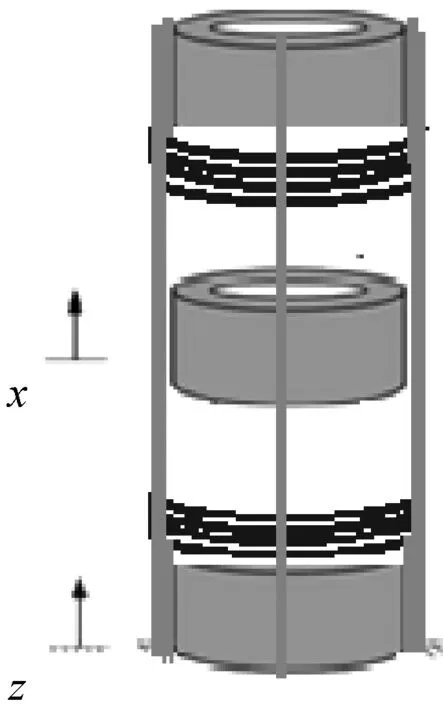
图1 磁力悬浮能量采集系统图Fig.1 A illustration of the magnetic levitation energy harvesting system
为了增加能量采集器的采集强度和采集频率的范围,在中间磁体下方悬挂一个线性振子。当磁悬浮结构受到外界环境的激励时,线性弹簧振子可以改变能量采集器的动力系统的特性,调节采集频率的带宽。这种能量采集器的力学模型如图2所示。
我们知道磁力的密度取决于中间磁体的距离,而距离可以通过系统的控制方程得到。当能量采集结构受到的外界激励是多频简谐激励时,考虑非线性磁力、重力和阻尼的影响,根据牛顿第二定律和法拉第定律可以得到控制方程

图2 磁力悬浮能量采集系统的力学模型图
Fig.2 A mechanical model schematic of the magnetic levitation energy harvesting system
(1)
2 谐波平衡法分析
由于磁悬浮能量采集器是强非线性激励系统,这里通过谐波平衡法对式(1)进行近似求解。为了将分析的问题一般化,首先对式(1)进行无量纲化,即引入如下无量纲参数
(2)
将以上无量纲参数(2)代入控制方程(1),得到无量纲化的动力学方程
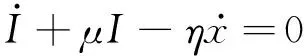
(3)
假设式(3)的解如下形式
(4)
将式(4)代入式(3),并令常数项,cosωt和sinωt的系数分别相等,得到稳态的情况下的幅频响应方程
a13η-a12k2-a11ω2-f1+3a01a11a21k3+
3a01b11b21k3=0
(5)
(6)
3a012a21k3+3/4a213k3+3/2a01a112k-3/2a01b112k33+
2b21c1ω-a22k2-2b22c2ω+
a21k1-4a21ω2-f2=0
(7)
2a21c1ω-b22k2+b23η+b21k1-4b21ω2=0
(8)
(9)
-4a22ω2-4a21ω2-f2+20b22c2ω+10a22k2=0
(10)
-4b22ω2-4b21ω2-20a22c2ω+10b22k2=0
(11)
-a12ω2-a11ω2-f1+10c2b12ω+10a12k2=0
(12)
-b12ω2-b11ω2-10a12ωc2+10b12k2=0
(13)
-b11ηω+a13μ+b13ω=0
(14)
a11ηω-a13ω+b13μ=0
(15)
-2b21ηω+a23μ+2b23ω=0
(16)
2a21ηω-2a23ω+b23μ=0
(17)
g1+10a02k2=0
(18)
对于给定的多频激励频率ω和激励频率比k,通过牛顿迭代法和弧长延长法求解式(5)~(18)中的14个未知数,即解得式(4)中的系数。从而可以分别求得式(3)的位移和电流的表达式,得到位移振幅和电流振幅幅频响应。
系统的电功率可以通过P=μI2计算,而在一个周期T=2π/ω的平均电功率可以表示为
(19)
3 系统参数对幅频响应的影响
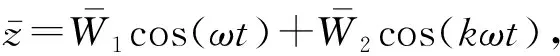
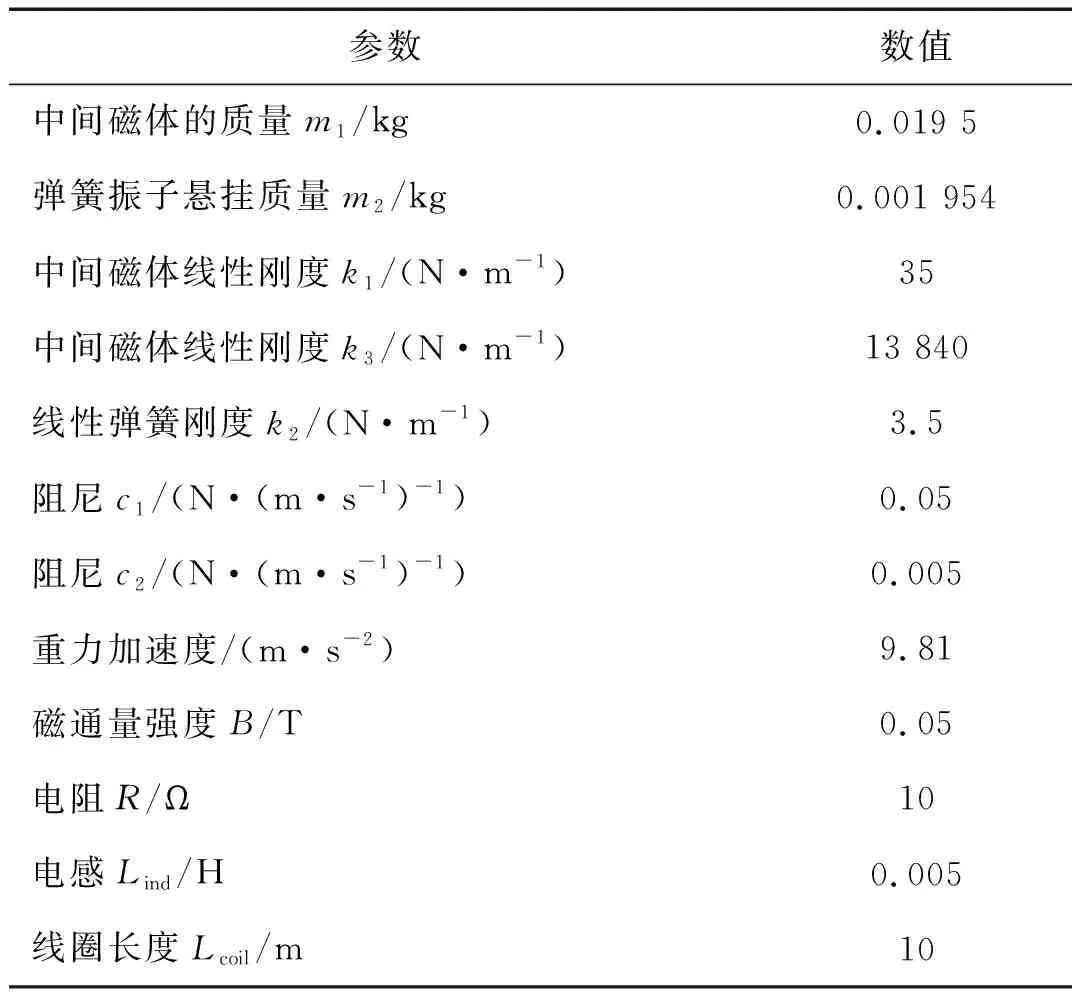
表1 系统的参数Tab.1 Parameters of the system
3.1 多自由度的质量比的影响
运用龙格库塔法,在保持其他参数不变的条件下,计算在不同的质量比u下中间磁体的平均功率幅频响应。在图3中,当质量比u=0.1时,磁悬浮能量采集系统的平均功率幅频响应分别在频率为3.8 Hz和7.5 Hz附近出现共振峰,两个带宽较窄的共振峰,振幅基本相等,并且都向右弯曲。当质量比u=0.1时,悬挂的振子质量过小,线性弹簧振子对能量采集系统的影响可以忽略不计。当质量比分别为u=1和1.5时,中间磁铁的平均功率都出现四个共振峰。增加的共振峰出现在左边,两个共振峰的频率分别为1 Hz和2 Hz附近,其峰值还不到单自由度左边峰值的一半;右边两个共振峰分别在频率为4 Hz和8 Hz附近出现,其峰值也小于单自由度右边的峰值,并且共振峰向右偏移。另外,从图3中还可以发现,左边的第一个共振峰的幅值随着质量比的增大而增大,且共振峰向左边偏移;但是右边的共振峰的幅值随着质量比的增大而变小,越向右边偏移,两个共振频率变大。此外,平均功率的左右两边的两个共振峰之间距离都随着质量比的增大而增大。
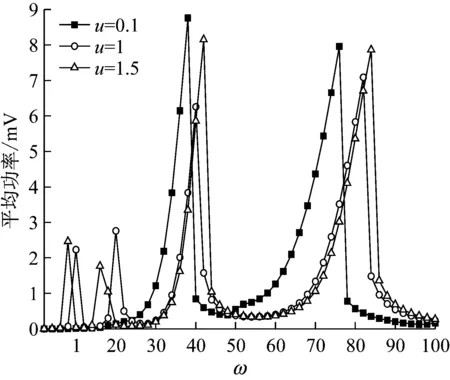
图3 在不同质量比下的弹簧振子平均功率幅频响应
Fig.3 Average power frequency response of middle magnet for different mass ratiou
图4给出中间磁体平均功率的幅频响应的数值验证。两个多频激励的加速度的振幅都是8 m/s2,多频频率比k=2。在线性弹簧的耦合下,共振峰由原来的两个增加到四个。平均功率向上扫频和向下扫频的四个共振峰,以及谐波平衡法和弧长延长法得到的解析解。平均功率的解析解和数值模拟解吻合较好。在共振峰附近有些误差,这是因为谐波平衡法的有限项的近似解代替真实解,产生了误差。我们可以通过增加谐波平衡近似解的项数来提高谐波解的精确度。
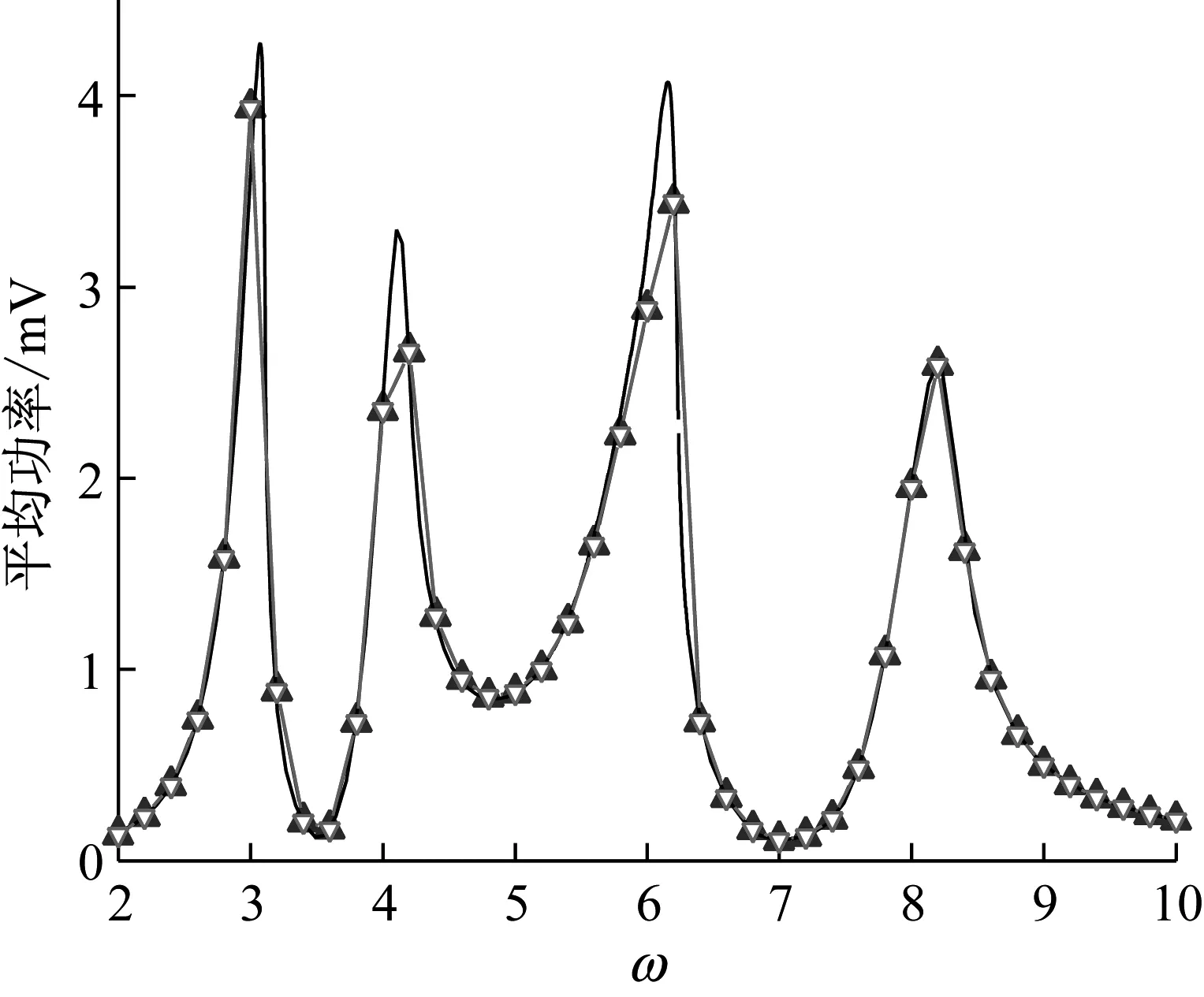
图4 平均功率幅频响应的数值验证
Fig.4 Numerical verification for the average power frequency response of middle magnet (k=2)
3.2 多自由度的阻尼的影响
接下来用谐波平衡法和弧长延长法,计算在不同中间磁体阻尼c1下中间磁体在多频激励下的平均功率幅频响应。除阻尼外,系统参数选取如表1所示。图5给出了阻尼c1分别取为0.04、0.05和0.055时的平均功率幅频响应。从图5中可以发现,系统平均功率幅频响应的四个共振峰随阻尼的减小而增大,带宽随阻尼的减小而增大和变宽,并且共振峰越向右弯曲。因此,两自由度系统阻尼的改变影响在多频激励下的平均功率的振幅和带宽。
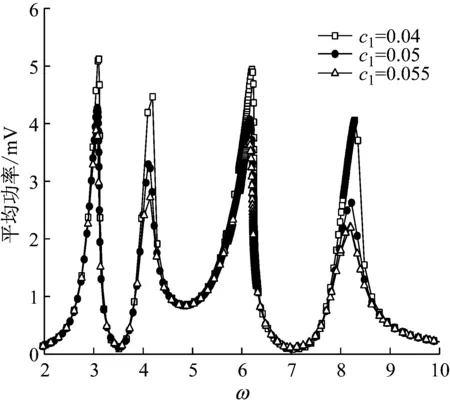
图5 不同阻尼的中间磁体平均功率幅频频响应
Fig.5 Average power frequency response of middle magnet for different dampingc
3.3 多自由度的电力耦合系数的影响
选取多自由度的耦合系数η分别取为0.3、0.5和0.8。从图6中发现,耦合系数取的越大,系统平均功率的幅频响应的四个共振峰越大,带宽越宽,并越向右弯曲。因此,系统电力耦合系数的增大时,中间磁体的平均功率的幅频响应反而变小。
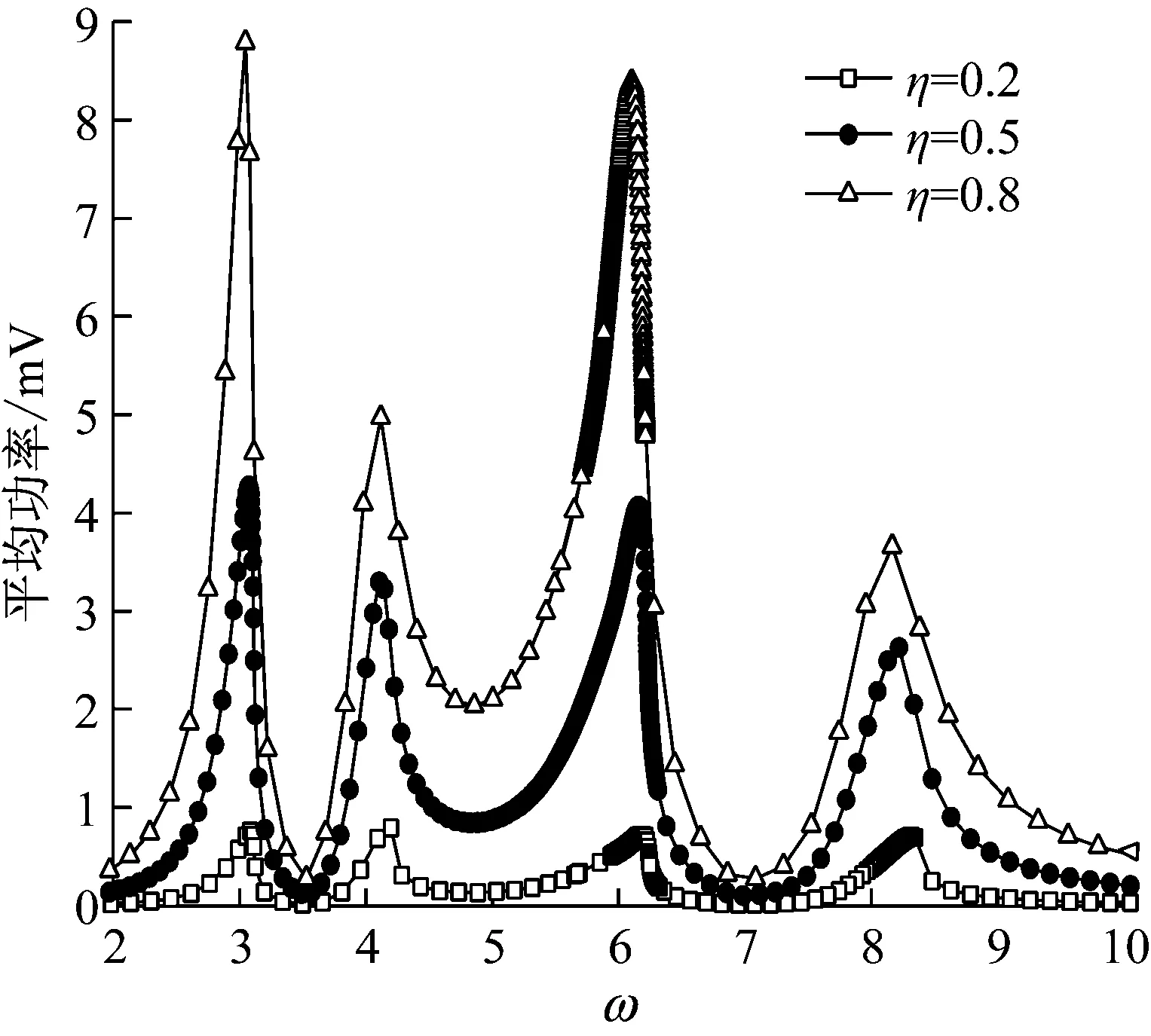
图6 不同耦合系数的中间磁体平均功率幅频频响应
Fig.6 Average power frequency response of middle magnet for different coupling coefficientη
4 结 论
本文研究了通过线性添加弹簧振子的多自由度的磁悬浮非线性能量器采集系统在多频激励下的非线性动力学响应。通过结合运用谐波平衡法、牛顿迭代法和弧长延伸法,近似解析分析能量采集系统在多频激励下中间磁铁的平均功率辐频响应,并通过直接数值方法验证解析分析。研究结果表明,这种多自由度的磁悬浮能量采集器质量比的增大时,在多频激励下的平均功率幅频响应的共振峰由两个变为四个共振峰,振幅变小,但两个共振峰的带宽变宽。另外,通过系统参数分析发现,调节系统参数阻尼比和耦合系数,可以优化得到增强两个共振峰和带宽的宽度,以达到增强振动能量采集效果的目的。

