体外预应力连续梁动力性能的能量法二阶分析

方德平

(华侨大学 土木工程学院, 厦门 361021)

体外预应力结构具有优良的力学性能，在国内外已得到普遍的应用[1]。已有较多的文献详尽地研究了体外预应力结构的静力性能[2]。不过，对其动力性能的研究，还有待进一步深入。Miyamoto等[3]采用正比假设，即体外筋预拉力的增量正比于梁跨中的振动位移，分析了体外预应力简支梁的动力性能，得出只适用于单一体外筋线型的自振频率计算公式。熊学玉等[4]采用正比假设，推导了适用于多种体外筋线型的简支梁计算公式。焦春节等[5-6]同样采用正比假设，在振动位移中，把体外筋对梁的预压力(简称体外预压力)和体外筋变形产生的弯矩，由面积相等的原则，转化为均匀分布的弯矩，得出双折线型体外筋的两跨连续梁振动微分方程，推导出连续梁正、反对称振型的自振频率计算公式，分析了体外预压力对连续梁自振频率的影响。在简支梁的动力性能分析中，方德平等[7]指出了正比假设中存在的一些问题，并提出新的合理假设以取代正比假设。在连续梁的动力分析性能中，方德平[8]也指出面积相等的原则和正比假设中存在的问题，也提出新的合理假设。方德平等认为其自振频率的解析解更接近于数值解，也更精确。

众所周知，从体系外对杆件施加的外轴力N会产生压缩软化效应，这一效应体现为外轴力产生的弯矩Ny，y为挠度。杆件的压缩软化效应减小了梁的自振频率，普通简支梁的自振频率

(1)

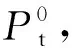
1 考虑体外筋第二阶变形的能量法

假设1：图1体外预应力连续梁的振动方程，yi=AiXi(x)sin(ωit),反对称第i振型为Xi(x)=sin(kix),kil=iπ,i=1,2,3,…；正对称左跨第i振型为Xi(x)=sin(kix)-fisinh(kix),fi=sin(kil)/sinh(kil),kil=(i+0.25)π,i=1,2,3,…；正、反对称振型取自普通连续梁的振型；假设2：张拉体外筋后，梁为直线；假设3：忽略梁的轴向变形，不考虑体外筋和转向座的质量。

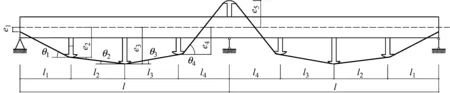
图1 体外预应力连续梁Fig.1 Externally prestressed continuous beam

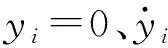
(2)

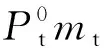
(3)

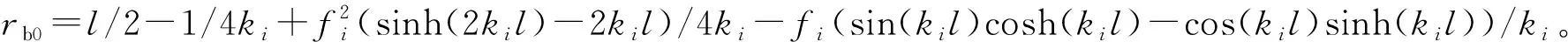
(4)

式中:lt，EtAt分别为体外筋的长度、抗拉刚度。

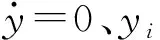
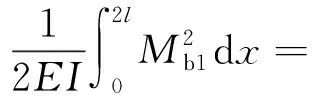
(5)

在计算体外筋第1阶和第2阶的变形之前，先讨论图2中线段OA的变形。线段OA在x，y轴方向上的变形分别为δx，δy，考虑二阶微分，线段OA的变形为

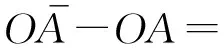
(cosθδy)2/2lA-sinθcosθδxδy/lA

(6)

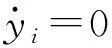
图2 线段OA的变形Fig.2 Deformation of line OA

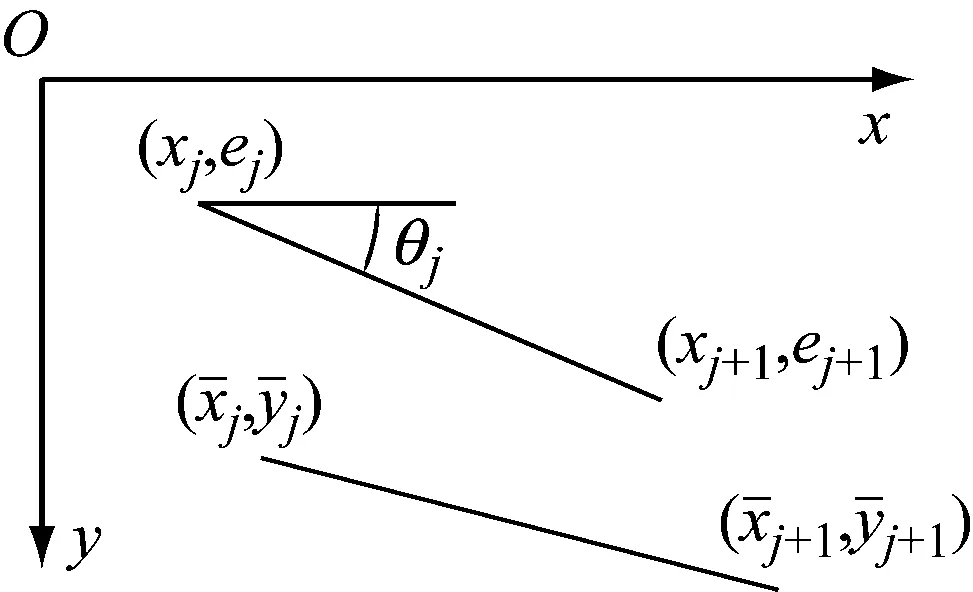
图3 体外筋线段的变形Fig.3 Deformation of external tendon segment

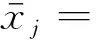
第j线段在x,y轴的变形δxj、δyj

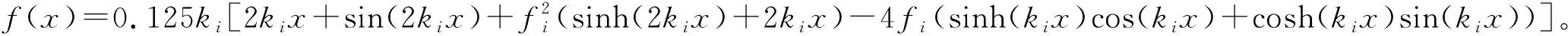
(7)

αj=djsinθj+cjcosθj,βj=bjcosθj+(cjsinθj)2/2lj+(djcosθj)2/2lj-cjdjsinθjcosθ/lj;θj，lj分别为第j线段的夹角、长度，如图1所示。体外筋的全部变形为

(8)

(9)

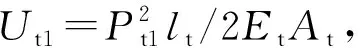
(10)

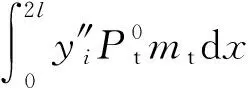
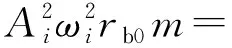
(11)

(12)

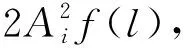
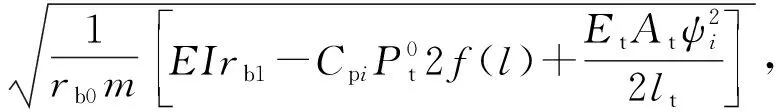
i=1,2,3,…

(13)

这样，当Cpi=1，体外预压力和外轴力的压缩软化效应相同；当Cpi=0，体外预压力无压缩软化效应。

2 算例分析

本文采用文献[8]的算例：砼梁长l=5 m，宽0.4 m、高0.15 m，E=32.5 GPa，单位长度质量m=0.8 t/m；体外筋Et=200 GPa、有效预应力σpe=1 000 MPa；l1=l2=l3=l4=1.25 m。分析两种线型(A和B)、两种偏心距(大偏心L和小偏心S)和两种体外筋面积，共8根梁AS1～BL2。A和B线型中e1=0，图1中的e2～e5见表1，转向座均位于抛物线上，体外预应力的等效荷载接近于均布荷载，是工程中常见的合理线型，A和B线型相差一个线性项，即两者的等效荷载相近。L偏心距是S偏心距的2倍。梁号的数字表示体外筋的根数，1，2表示At=137 mm2、274 mm2。

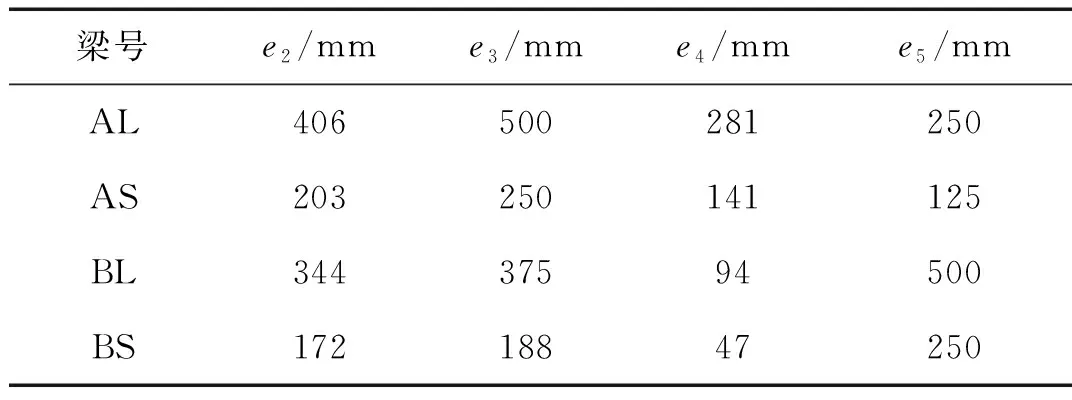
表1 体外筋线型和偏心距Tab.1 The configurations and eccentricities of external tendons

表2为直线型体外筋影响系数Cpi与接触点数量n之间的关系，表3为抛物线型AL体外筋影响系数Cpi与接触点数量n之间的关系，其他抛物线型AS、BL和BS的计算结果与AL线型的结果相近，不赘述。表2的直线型体外筋位于梁轴线，接触点沿梁长度等间距分布。从表2、3可知：体外预压力的影响系数Cpi主要于接触点数量n相关，于体外筋线型的关系微弱。从表2可以看出：当只有3个接触点，即跨间无转向座时，体外筋存在最大的偏心距损失，影响系数Cpi=1，体外预压力和外轴力的压缩软化效应相同；当接触点数量n从最小值3开始增加，体外筋偏心距损失逐渐减小，体外筋逐渐接近于无黏结筋，影响系数Cpi从1逐渐降低至接近于0，体外预压力的压缩软化效应减少至接近于0。这与Hamed等的结论相一致，无黏结预压力无压缩软化效应。随着振型阶数的提高，振型中反弯点之间的间距减小，反弯点之间的接触点数量减少，相当于减少了第1振型中的接触点数量，因而增大了影响系数。

表2直线型体外筋影响系数Cpi与接触点数量n之间的关系

Tab.2RelationshipbetweeninfluencecoefficientCpiandthenumberofcontactpointsnforstraighttendon

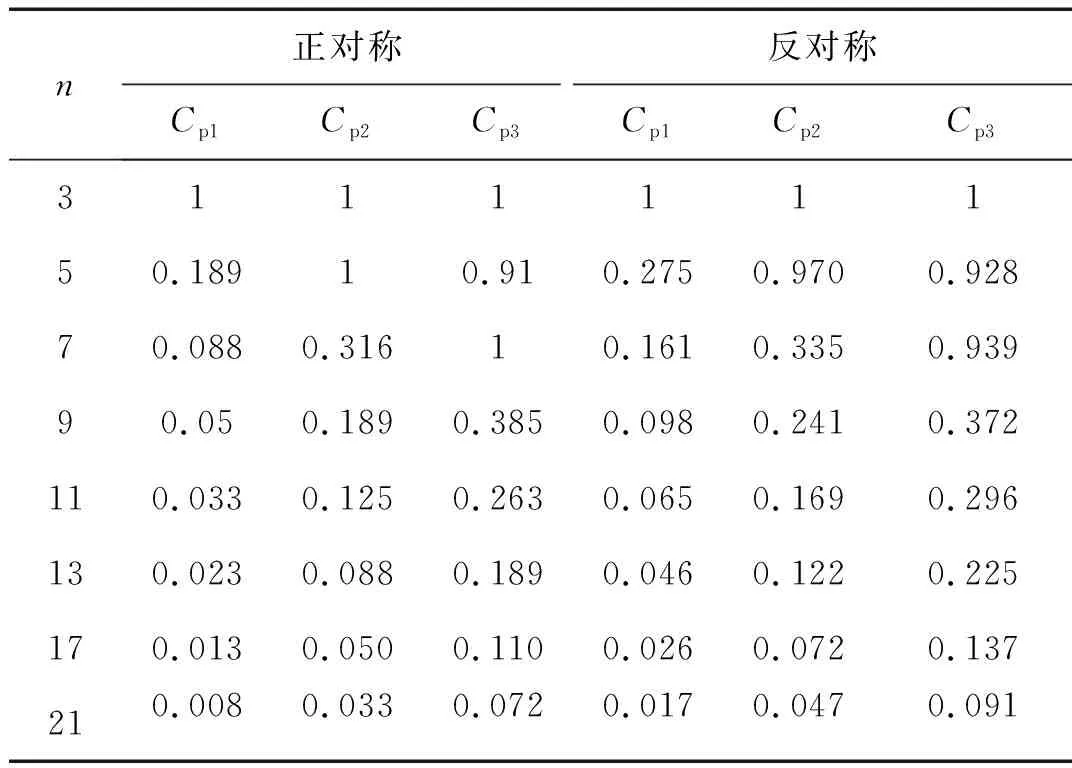
n正对称反对称Cp1Cp2Cp3Cp1Cp2Cp3311111150.18910.910.2750.9700.92870.0880.31610.1610.3350.93990.050.1890.3850.0980.2410.372110.0330.1250.2630.0650.1690.296130.0230.0880.1890.0460.1220.225170.0130.0500.1100.0260.0720.137210.0080.0330.0720.0170.0470.091

表3AL线型体外筋影响系数Cpi与接触点数量n之间的关系

Tab.3RelationshipbetweeninfluencecoefficientCpiandthenumberofcontactpointsnforALtendon

n正对称反对称Cp1Cp2Cp3Cp1Cp2Cp350.1970.8980.9670.3040.9010.94470.0360.3350.960.150.3620.92190.0250.1270.4280.0780.2140.412110.0120.0450.2080.0370.1350.271130.0100.0200.1130.0130.0810.195170.0060.0110.0180.010.0190.093210.0030.0060.0100.0050.0100.037

表4为8根AS1～BL2梁第1～4自振频率的计算值，ω1,ω3为第1、2反对称振型的频率，ω2,ω4为第1、2正对称振型的频率。方法①是本文提出的方法；方法②是文献[8]的方法，方法③是数值法。理论值的正确性一般应由实验值来验证，不过这并不适用于预应力砼结构。预应力的施加闭合了砼的微裂缝，增强了梁的刚度，反而增大了梁实测的自振频率，无法验证压缩软化效应。因此本文采用数值解来验证理论值的正确性。体外筋的拉力沿长度不变，体外筋与转向座之间可以无摩擦滑动，对此，数值模拟的简明办法：在转向座两侧体外筋的角平分线上增设接触单元，接触单元和体外筋单元均为桁架单元，只承受轴力，如图4所示。角平分线上增设的接触单元即可模拟无摩擦滑动，又可保证两侧体外筋拉力相等。接触单元长度为1 cm，EA与体外筋的EtAt相同；转向座单元刚度取10倍梁的刚度，模拟其刚性。用集中质量法求解频率和振型，其方程为

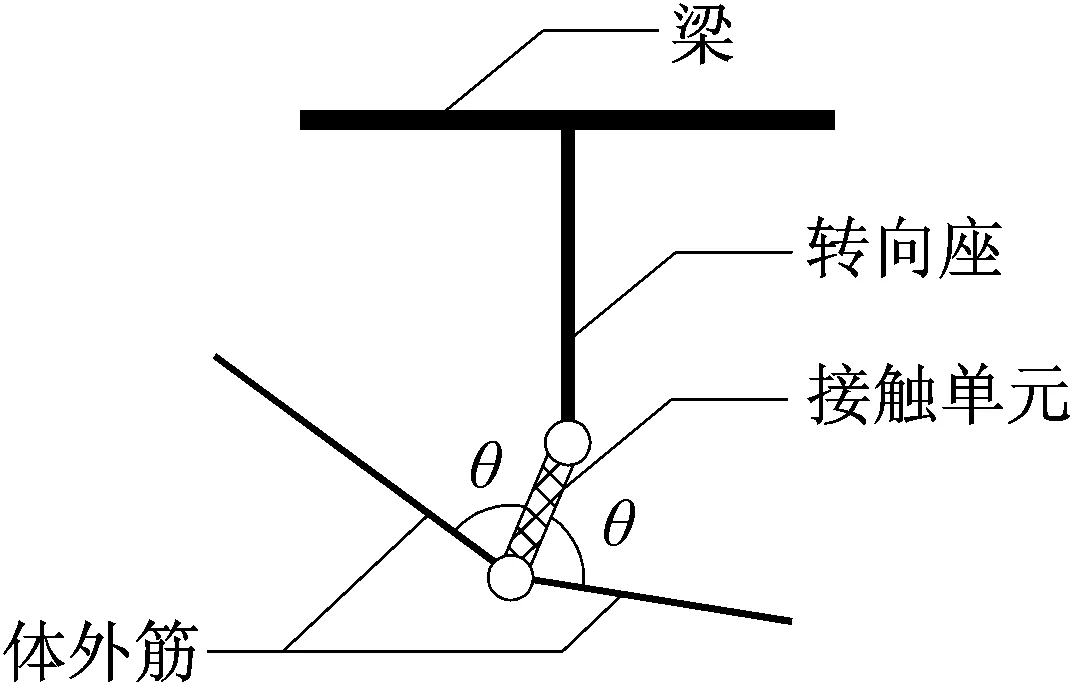
图4 接触单元Fig.4 Contact element

(14)

式中:[δ]为梁集中质量处的竖向柔度矩阵；[M]为集中质量对角矩阵，{yi}为第i振型，ωi为第i自振频率。用广义雅克比法求出自振频率和振型。柔度矩阵[δ]包含了砼梁的EI和长度，体外筋的EtAt和长度，转向座位置、高度，体外筋与转向座之间的无摩擦滑移等因素。在梁单元的刚度矩阵[K]中，考虑了体外预压力的影响系数Cpi

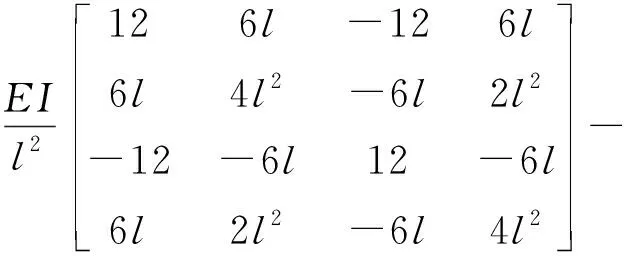
(15)

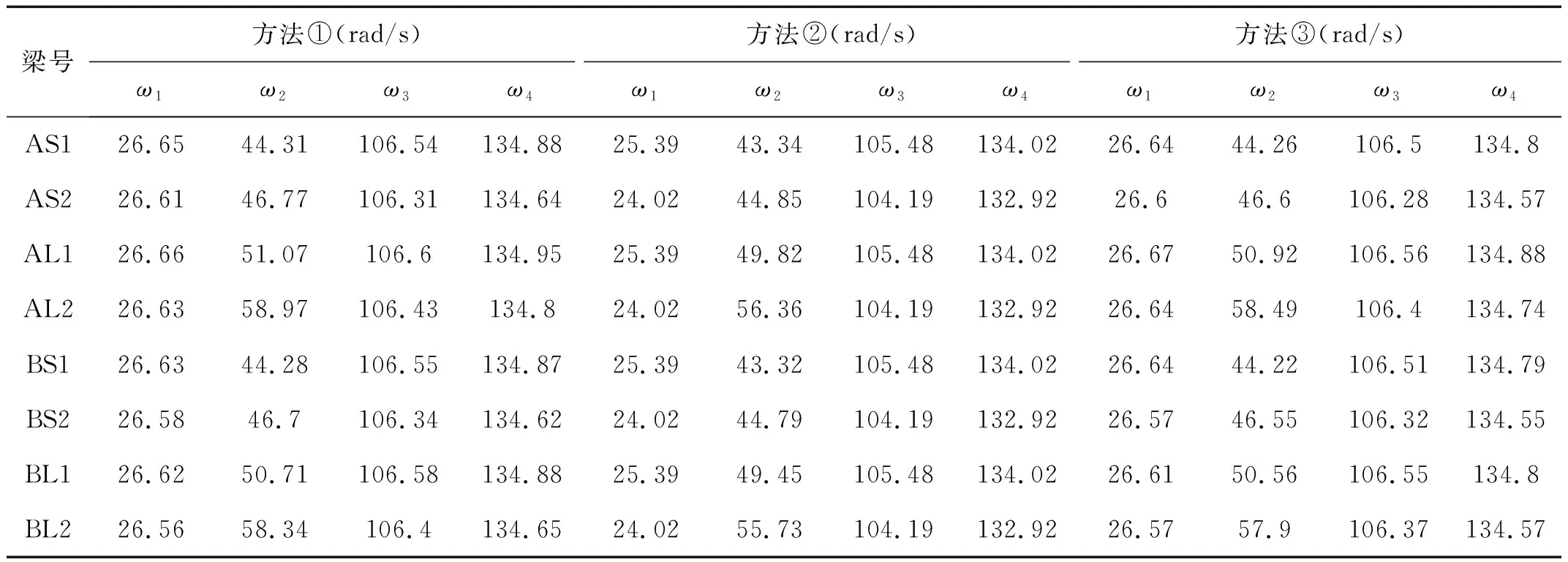
表4 体外预应力梁第1～4自振频率的计算结果Tab.4 The 1st—4th natural frequency Calculation results of externally prestressed beam

表5 无预压力梁的ω2、ω4Tab.5 ω2, ω4 of beams without prestress force

3 结 论

外轴力压缩软化的影响系数为最大值1，有最大的压缩软化效应。无黏结预压力的影响系数为最小值0，没有压缩软化效应。体外预应力筋存在偏心距损失，体外预应力梁的刚度小于相同形状的无黏结预应力梁的刚度，因而体外预应力梁的自振频率低于无黏结预应力梁的频率。这说明体外预压力存在压缩软化效应，并且已经研究了体外预应力简支梁预压力的压缩软化效应。本文用能量法对体外预应力连续梁的自振频率进行了二阶分析，阐明了连续梁体外预压力的压缩软化效应。研究结论如下：

(1) 体外预压力的影响系数介于0～1，梁的转向座数量决定了体外预压力的影响系数的大小。跨间无转向座时，体外筋存在最大的偏心距损失，影响系数等于1，体外预压力与外轴力具有相同的压缩软化效应；增加转向座数量，减小了偏心距损失，体外筋逐渐接近于无黏结筋，影响系数从1逐渐降低至接近于0。

(2) 体外预压力和梁第1阶稳定临界荷载比值一般比较小，当跨间至少有1个转向座时，影响系数Cp1明显小于1，体外预压力的第1阶压缩软化效应很小；部分的Cp2、Cp3值虽接近1，但体外预压力对第2、3阶自振频率的影响也很小。总之，可以忽略体外预压力对各阶自振频率的影响。

(3) 由于反对称振型不产生体外筋的第一阶变形，体外筋只产生可忽略的压缩软化效应，所以可忽略体外筋对其自振频率的影响。体外筋只明显地影响梁的ω2(第1阶正对称频率)，增加体外筋的偏心距和面积，梁的刚度随之增加，增大了ω2。不过，其他阶的正对称振型产生体外筋的变形很小，可忽略体外筋对其自振频率的影响。即只考虑体外筋对第1阶正对称频率的影响，忽略对其他频率的影响。