考虑黏性效应的爆破震动区的理论分析

李志文, 李建春, 洪胜男, 李海波, 张国凯,3

(1. 中国科学院武汉岩土力学研究所 岩土力学与工程国家重点试验室， 武汉 430071；2. 中国科学院大学， 北京 100049； 3. 南京理工大学 机械工程学院， 南京 210094)

一般认为在炸药在岩体爆炸过程中，在爆炸冲击应力波和爆生气体的联合作用下，从炮孔壁往外依次形成粉碎区、破碎区和未开裂的震动区[1-2]，同时高幅值的冲击波转变为低幅值的地震波继续向外传播。爆破地震波在传播过程中，由于波阵面的扩散和介质的吸收作用，其幅值和频率都会发生一系列的变化，这种变化对地面建筑的安全存在重要影响，因此研究爆破地震波的产生和传播规律具有现实意义。爆破地震波的产生和传播的研究方法主要有现场试验、数值模拟和理论分析等。如张永哲[3]通过现场实测数据，分析了爆破地震波的地表峰值强度的衰减规律，并给出质点速度和频率随爆源距离以及装药量的关系式。龙源等[4]分析大量爆破地震波测试数据，得出高频率成分比低频成分衰减更快，地形条件的改变对频率影响较明显等结论。Singh[5]通过对临近露天爆破的地下煤矿进行振动监测，发现煤矿顶部的振幅大于立柱，且矿顶与立柱连接处的振幅更大。李重情等[6]通过现场试验研究了混凝土中不同埋深的爆炸冲击波的传播规律，指出爆炸冲击质点应力峰值随装药比例埋深的增加以及混凝土强度的增加而增大。赵明生等[7]基于单孔爆破试验，分析了段药量对爆破振动信号时频特性的影响，发现随着段药量的增加，爆破振动信号的低频能量所占总能量的比例增加且爆破振动的持续时间延长。现场试验方法的缺点是费用较高，且难以监测靠近爆源处的质点振动。而数值模拟具有成本低，可重复性强等优点，被广泛用于爆破地震波传播的研究的，如赵坚等[8]结合UDEC和AUTODYN-2D模拟节理岩体中爆炸波的传播和节理对波传播的影响，得出岩体中节理的存在使波衰减很快，且较低刚度的节理产生的较大衰减的结论。夏祥等[9]运用离散元方法模拟了节理岩体距爆源不同处质点的振动速度和频率的变化特征，并确定了岩体质点最大振动速度和振动主频随爆源距离的衰减规律。李鹏等[10]和周俊汝等[11]分别采用LSYDNA程序模拟单孔装药下爆破地震波传播，发现爆炸荷载及装药结构均会对爆破地震波主频衰减规律造成影响。数值模拟对研究炸药爆炸过程和复杂地质地形条件下的爆破地震波传播具有很大优势，但对于爆破地震波的产生和传播缺乏机理性的解释，对此解析方法具备天然优势，如Li等[12-13]采用波传播理论分析了硐室爆炸下的地表和邻近硐室的响应，揭示了周围结构的振动与应力波的传播路径及多次反射相关，并得出了地表和邻近隧道PPV的分布规律，与数值模拟对比具有较好的一致性。考虑到岩体对爆破地震波能量的耗散，可把岩体视为黏弹性介质[14-15]。爆破地震波在震动区边界上产生，在震动区内部传播，可将爆破荷载等效地作用在震动区边界上[16-17]。基于上述认识，本文将岩体考虑成Kelvin-Voigt介质，并在其内设置单个球形空腔，然后在球腔边界均匀地施加三角形爆破荷载，最后采用傅里叶变换法从频域求解该问题，得到质点位移和速度关于频率的积分解。通过数值积分和参数分析，得到几种爆破荷载参数和黏弹性介质力学参数对爆破地震波的产生和传播的影响规律。

1 计算模型与求解

在无限Kelvin-Voigt介质中取半径为a的球形空腔作为震动区边界，从零初始时刻开始，在空腔壁均匀地施加爆破荷载，而后爆破地震波均匀地向四周传播。取φ为标量位移势，则符合波动方程[18]

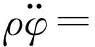
(1)

式中：ρ为介质密度；λ和μ为弹性拉梅系数；λ′和μ′为黏性拉梅系数；在Kelvin-Voigt介质模型中，给定弹性模量E和黏性系数η以及泊松比ν，可以求出相应的弹性拉梅系数λ和μ，以及黏性拉梅系数λ′和μ′[19]

(2)

初始条件

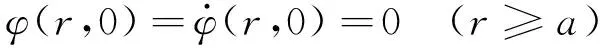
(3)

边界条件

σr(a,t)=-P(t)

(4)

式中：σr为径向应力；P(t)为作用于空腔壁的三角形爆破荷载；三角形爆破荷载峰值为P0；上升时间为τ1；总持续时间为τ2，其数学形式如下

(5)

径向应力和应变的关系和应变与径向位移的关系分别为

(6)

θ=∂ur/∂r+2ur/r

(7)

εrr=∂ur/∂r

(8)

式中：θ为体应变；εrr为径向应变；ur为径向位移。

联立式(4)、(6)、(7)和(8)得

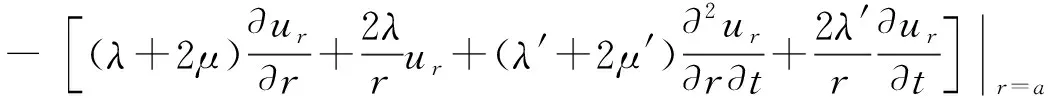
(9)

再将径向位移与标量位移势的关系式：ur=∂φ/∂r,代入式(9)得

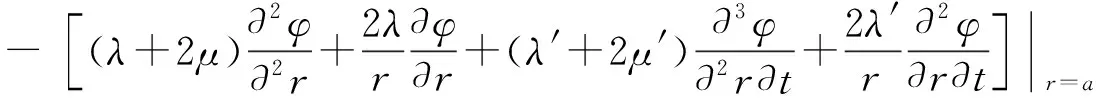
(10)

通过傅里叶正变换和逆变换把位移势函数φ(r,t)与爆破荷载P(t)写成傅里叶积分形式如下

(11a)

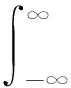
(11b)

(12a)

(12b)

将式(11a)代入式(1)中，并化简得

(13)

将式(11a)与(12a)代入到式(10)，并化简得

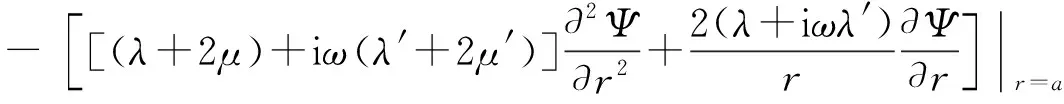
(14)

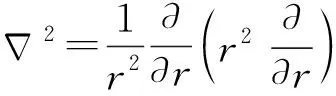
(15)

(16)

令φ(r)=eikr/r代入式(15)和(16)中，得

(17)

(18)

式中B(ω)=[(λ+2μ)+iω(λ′+2μ′)](-k2a2-2ika+2)+2(λ+iωλ′)(ika-1)

于是得标量位移势函数的频谱函数如下

(19)

再将式(19)代入式(11a)中得到位移势函数

(20)

又因为ur=∂φ/∂r，于是得到径向位移函数

(21)

由傅里叶变换的性质可知，式(21)的积分项中的实部是关于频率的偶函数，虚部是关于频率的奇函数，所以有

ur(r,t)=

(22)

式中：Re()表示取复数的实部。

令复波数k=kr+iβ，其中kr是实波数，β为吸收因子，由于爆破地震波向外传播，所以kr必须小于零，而为满足介质的吸收衰减作用，β必须大于零。于是解式(17)得

(23a)

(23b)

式中:τv为黏性系数和弹性模量比值，τv=η/E，cp为弹性介质中纵波波速，cp=(λ+2μ/ρ)1/2。

联立式(5)和式(12b)求出爆破荷载的频谱函数P(ω)

(24)

将式(23)和式(24)代入积分式(22)中，即得到该问题的积分形式的位移解。对式(22)求时间导数得到积分形式的速度解

vr(r,t)=

(25)

2 爆破地震波的产生及其影响因素

结合式(22)和式(24)可知，影响爆破地震波的产生的主要因素有黏弹性介质的力学参数：如弹性模量和黏性系数等，和爆破荷载参数：爆破荷载峰值、爆破荷载上升时间和爆破荷载总持续时间。爆破荷载峰值显然是与爆破地震波幅值成正比的，其他因素对爆破地震波的影响将通过对式(22)和(25)进行数值积分和参数分析来说明。

2.1 爆破荷载上升时间和总持续时间

为确定爆破荷载上升时间对爆破地震波的产生的影响，数值积分中取介质的密度ρ=2.5×103kg/m3，弹性模量E=20 GPa，黏性系数η=0 MPa·s，泊松比v=0.3，球腔半径a=2 m，爆破荷载峰值P0=50 MPa，爆破荷载总持续时间τ2=10 ms，爆破荷载上升时间分别为τ1=1.0、1.5、2.0、2.5、3.0 ms。得到震动区边界质点的位移和速度时程曲线，如图1和图2所示。

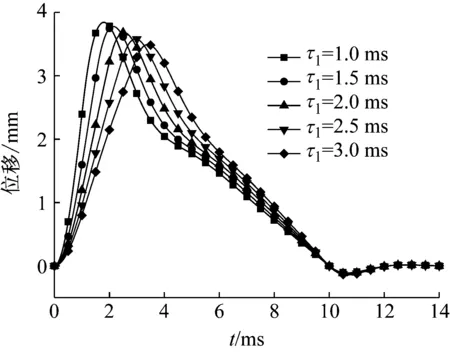
图1 不同τ1下的震动区边界质点位移Fig.1 Boundary particle displacement of vibrational zone under different τ1

由图1和2可知，在相同爆破荷载峰值和总持续时间下，随荷载上升时间增加，震动区边界的位移和速度幅值减小。这是因为随荷载上升时间增加，荷载达到峰值前爆破地震波传播的距离变远，导致介质中产生运动的质量增大，即介质抵抗运动的惯性增大造成的。位移和速度时程曲线的持续时间不随荷载上升时间而改变，但相对于爆破荷载总持续时间τ2略有增加。这是因爆破荷载作用完成，介质中积蓄的弹性势能使震动区边界回弹所致，由图2可看出，位移时程曲线在10～12 ms之间存在一段负值，由图3可看出，在时间为10 ms时，速度时程曲线由一近似恒定负值开始趋于大于零。

图2 不同τ1下的震动区边界质点速度Fig.2 Boundary particle velocity of vibrational zone under different τ1

为确定爆破荷载总持续时间对爆破地震波的产生的影响，数值积分中取爆破荷载上升时间τ1=2 ms，爆破荷载总持续时间分别为τ2=6、8、10、12、14 ms，其余参数选取同前，得到震动区边界质点的位移和速度时程曲线，如图3和图4所示。

图3 不同τ2下的震动区边界质点位移Fig.3 Boundary particle displacement of vibrational zone under different τ2

由图3和4可知，在相同爆破荷载峰值和上升时间下，随荷载总持续时间的增加，震动区边界的位移和速度幅值几乎不变，而位移和速度时程曲线持续时间增加。结合上条结论，可知爆破荷载上升时间影响爆破地震波的幅值，爆破荷载总持续时间影响爆破地震波的持续时间。

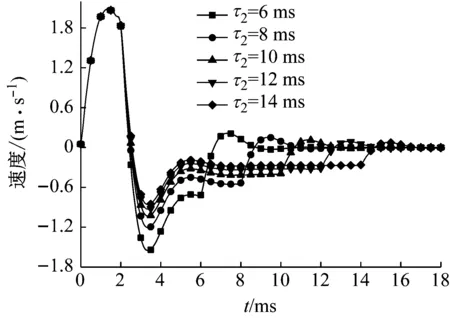
图4 不同τ2下的震动区边界质点速度Fig.4 Boundary particle velocity of vibrational zone under different τ2

2.2 介质的弹性模量和黏性系数

为确定弹性模量对爆破地震波的产生的影响，数值积分中取爆破荷载上升时间τ1=2 ms，爆破荷载总持续时间τ2=10 ms，弹性模量为别为E=10、15、20、25、30 GPa，其余参数选取同前，得到震动区边界质点的位移和速度时程曲线，如图5和图6所示。

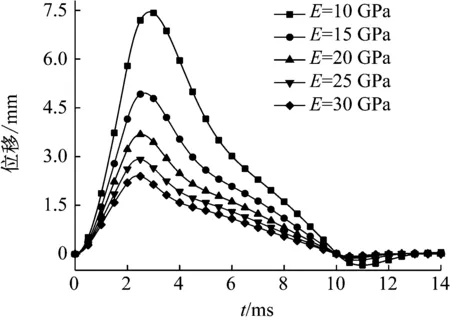
图5 不同E下的震动区边界质点位移Fig.5 Boundary particle displacement of vibrational zone under different E

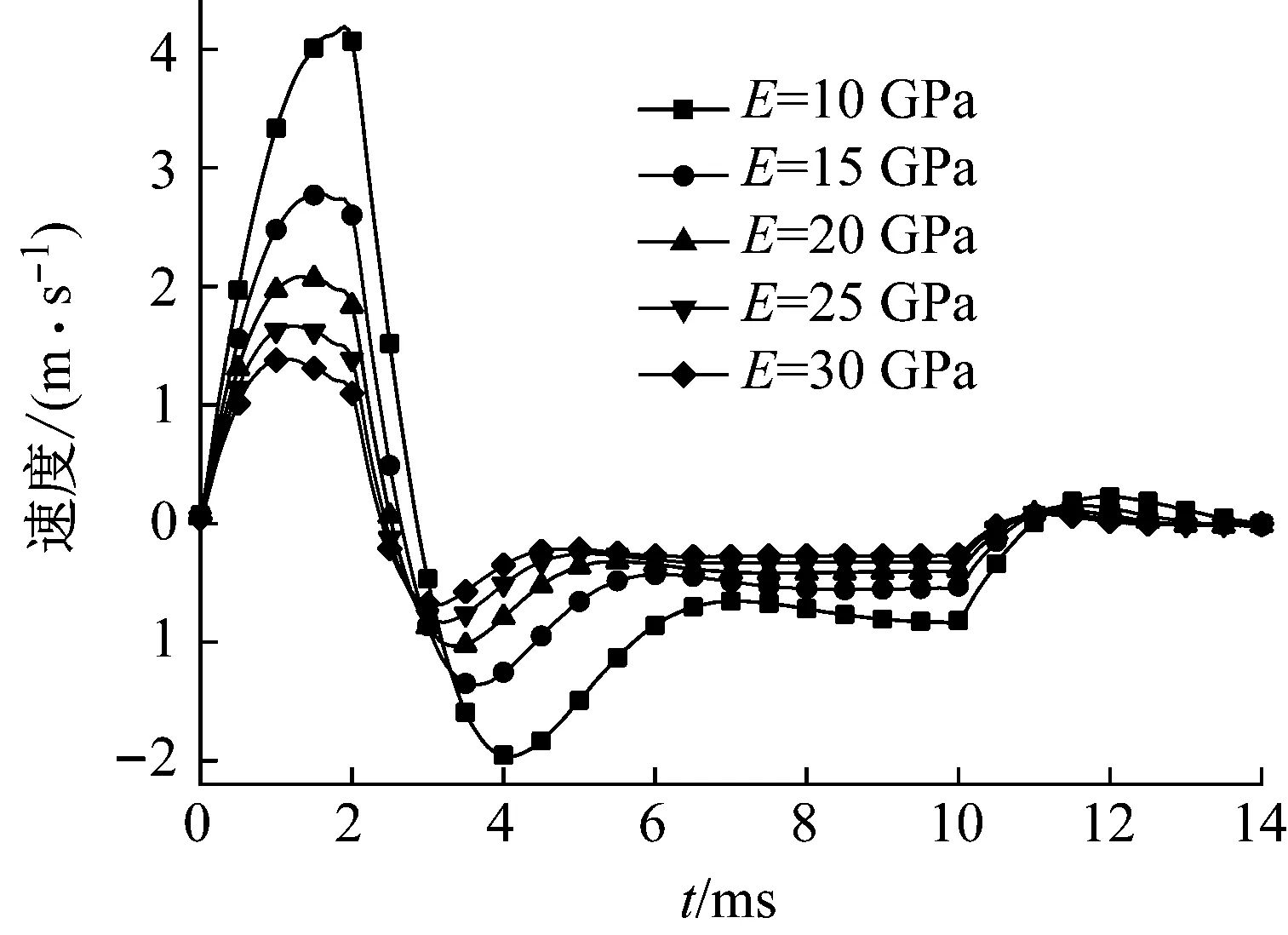
图6 不同E下的震动区边界质点速度Fig.6 Boundary particle velocity of vibrational zone under different E

由图5和6可知，在相同爆破荷载作用下，随介质的弹性模量增大，震动区边界上位移和速度幅值减小，且位移和速度时程曲线的持续时间略微减短。这是因为震动区边界的刚度与介质弹性模量是成正比的，相同爆破荷载作用下，随震动区边界的刚度增大，震动区边界位移和速度幅值减小，介质储存的弹性势能减少，因此震动区边界的回弹时间也变短。

为确定黏性系数对爆破地震波的产生的影响，数值积分中取弹性模量E=20 GPa，黏性系数分别为η=0、5、10、15、20 MPa·s，其余参数选取同前，得到震动区边界质点的位移和速度时程曲线，如图7和图8所示。

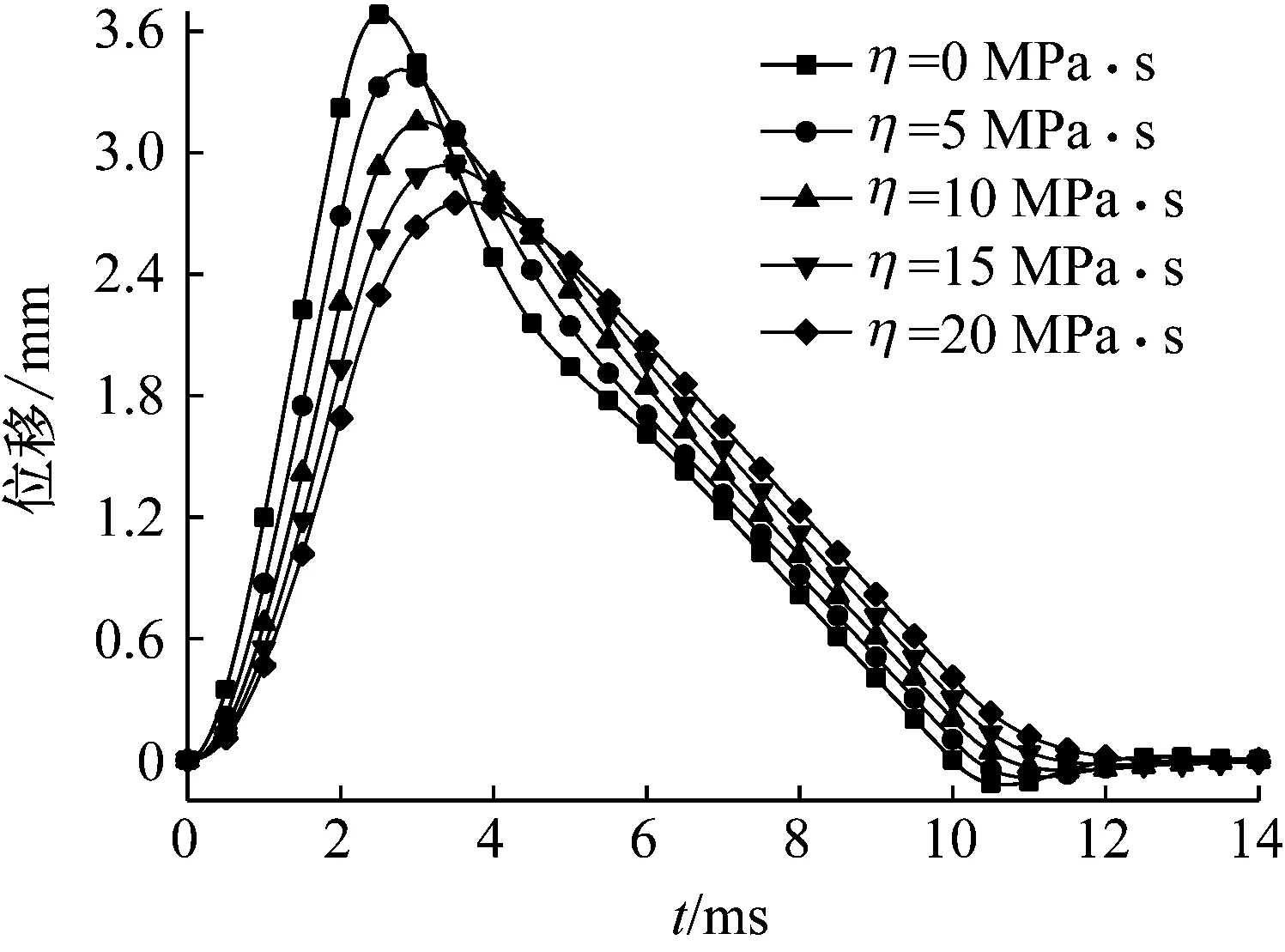
图7 不同η下的震动区边界质点位移Fig.7 Boundary particle displacement of vibrational zone under different η

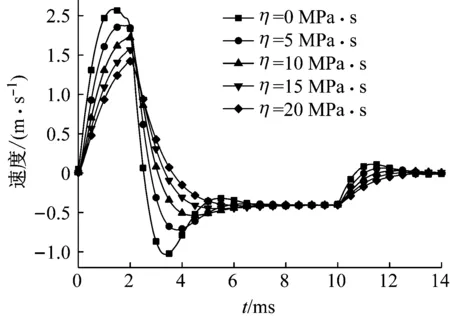
图8 不同η下的震动区边界质点速度Fig.8 Boundary particle velocity of vibrational zone under different η

由图7和8可知，在相同爆破荷载作用下，随介质的黏性系数增大，震动区边界上位移和速度幅值减小，而位移和速度时程曲线的持续时间略微增长。这是因为Kelvin-Voigt介质采用弹簧和黏壶并联方式进行力的传导，介质的弹性模量相同时，黏性系数越大，介质在动力作用下的有效弹性模量也越大，震动区边界的有效刚度也越大，因此相同爆破荷载作用下的位移和速度幅值则越小，又因为介质的黏滞性增加，导致介质变形运动的时间也增长。

3 爆破地震波的传播规律

3.1 爆破地震波的几何衰减规律

由于波阵面的几何扩散与介质的吸收作用，随传播距离增加，爆破地震波在介质中很快地衰减。由式(22)和式(25)可知，质点位移解和速度解由两部分组成，一部分与r2成反比，另一部分与r成反比，可见几何衰减的速率介于二者之间，为了表明这种关系，取介质的黏性系数η=0 MPa·s，以排除介质吸收作用的影响，其余参数如下：v=0.3，ρ=2.5×103kg/m3，P0=50 MPa，τ1=2 ms，τ2=10 ms，a=2 m，E=20 GPa。得到质点位移和速度幅值及其衰减速率与爆源距离的关系，如图9和图10所示。图9和10中，位移和速度峰值衰减速率由平均每米衰减的百分比定义。

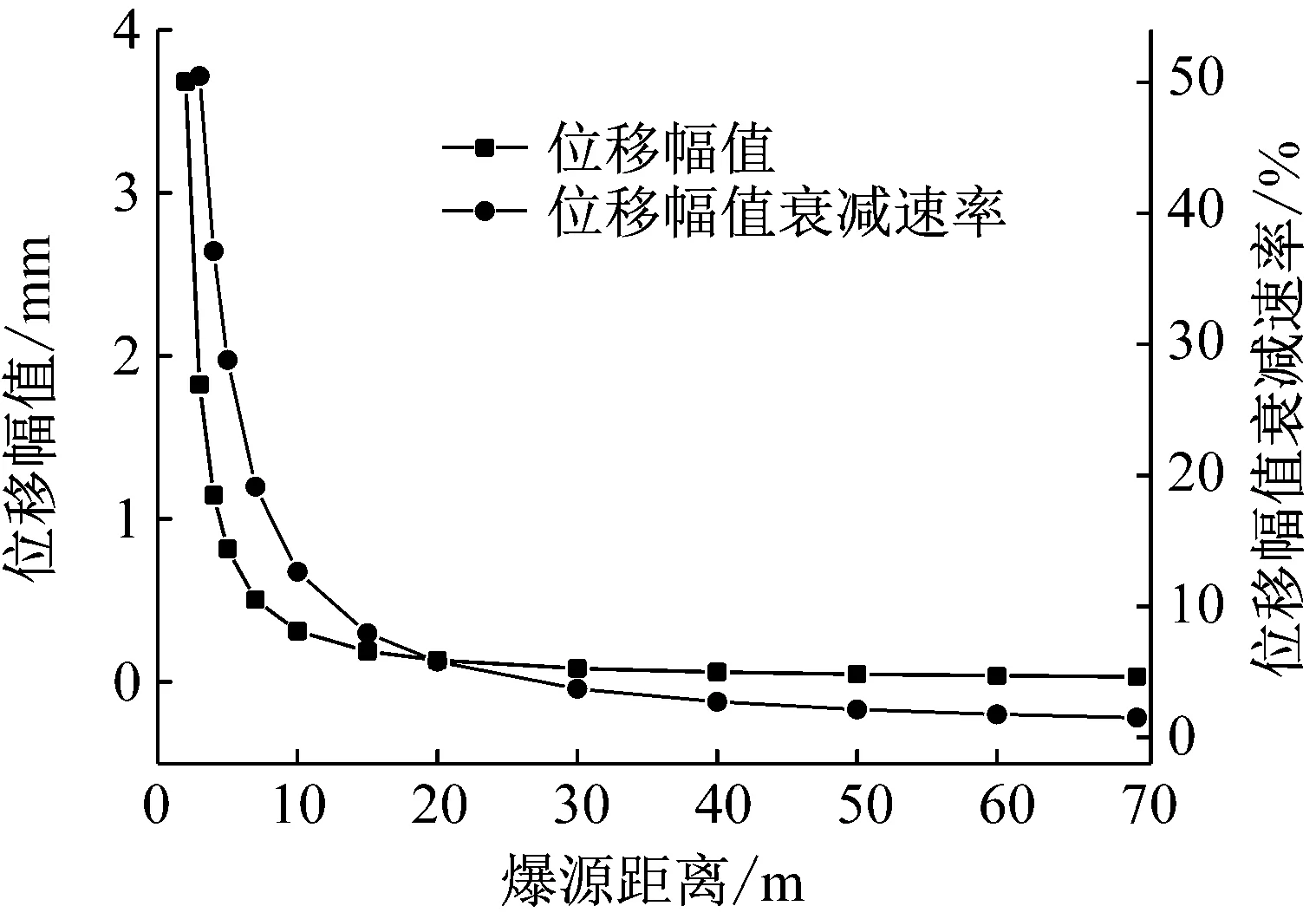
图9 位移幅值和幅值衰减速率与爆源距离的关系Fig.9 Relation between displacement amplitude and amplitude decay rate with burst source distance

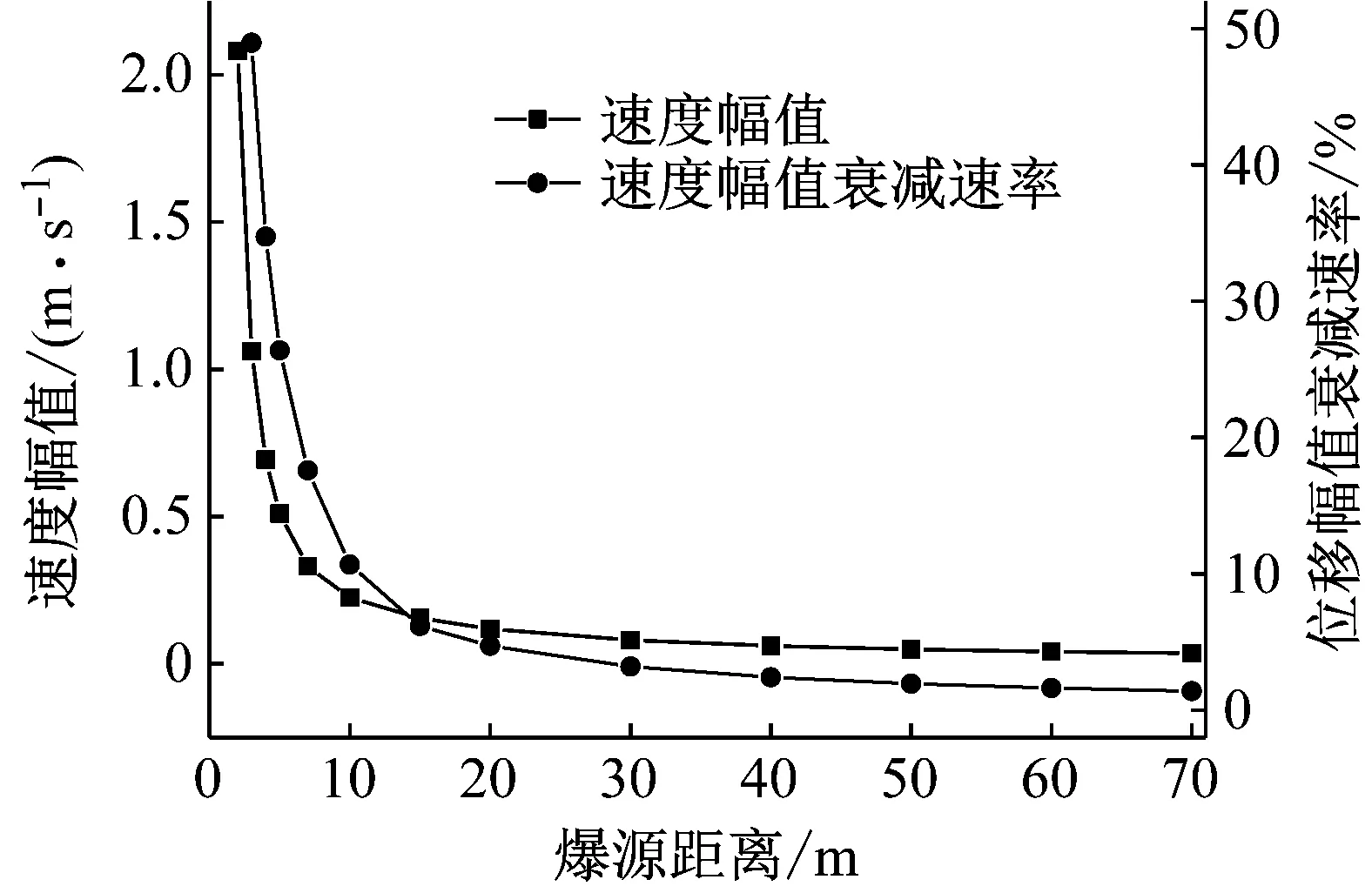
图10 速度幅值和幅值衰减速率与爆源距离的关系Fig.10 Relation between velocity amplitude and amplitude decay rate with burst source distance

由图9和10可知，在靠近震动区边界处，爆破地震波位移和速度的幅值衰减速率都很大，随着传播距离增加衰减速率开始减小，在爆源距离r达到20 m后，质点位移和速度幅值都趋于稳定，而此处的位移和速度幅值衰减速率分别为5.8%和4.7%，接近1/r，于是可将r大于的20 m的区域定义为爆破震动远区，r小于20 m的区域定义为爆破震动近区，在爆破震动远区位移和速度的几何衰减速率等于1/r，在爆破震动近区位移和速度的几何衰减速率大于1/r，这与前人的研究结果是一致的[20]。

3.2 爆破地震波的材料衰减特性

爆破地震波在黏弹性介质中传播过程中，会发生振幅谱的衰减和相位谱的弥散，导致波形幅值的降低和频率成分的改变，即介质对爆破地震波产生了吸收衰减作用，而这种吸收衰减作用主要与介质的弹性模量和黏性系数相关，可通过对式(22)和(25)进行数值积分和参数分析进行说明。首先，研究弹性模量对介质吸收能力的影响，在数值积分中取黏性系数η=10 MPa·s，弹性模量分别为E=10，15，20，25 GPa，其余参数同前，得到不同爆源距的位移和速度幅值。为衡量介质对爆破地震波的吸收作用，用不同爆源距处的位移和速度幅值与震动区边界的位移和速度幅值作百分比，以排除震动区边界振动幅值不同对分析的干扰，它们的百分比越小，则介质对爆破地震波的吸收能力越强，结果如图11和图12所示。

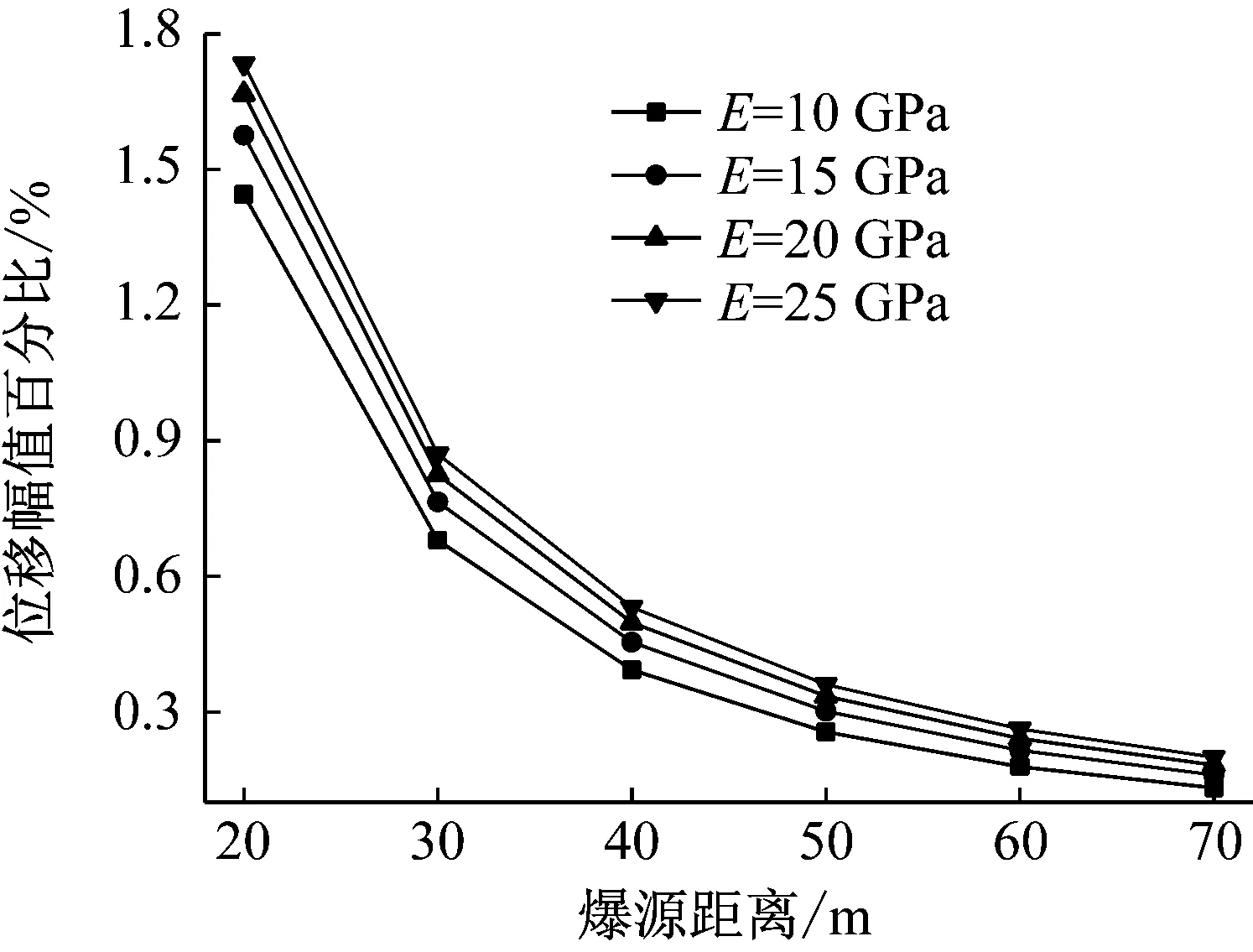
图11 位移幅值百分比与爆源距离的关系Fig.11 The relationship between the displacement amplitude percentage and the source distance

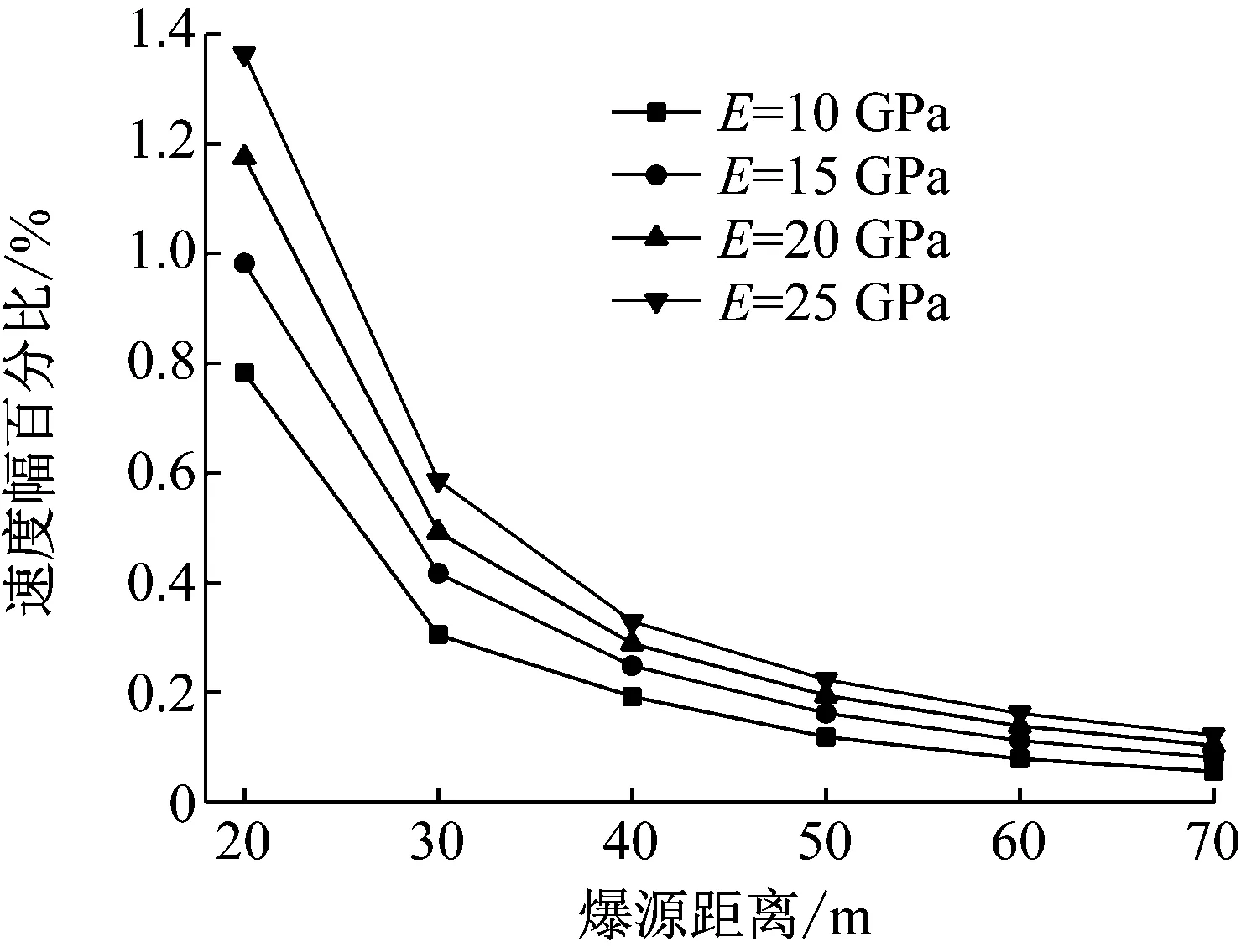
图12 速度幅值百分比与爆源距离的关系Fig.12 The relationship between the velocity amplitude percentage and the source distance

由图11和12可知，介质的弹性模量越大，介质对爆破地震波的吸收衰减作用越弱。虽然在相同爆破荷载作用下，介质的弹性模量越低，震动区边界的振动幅值越大，但可预计随着传播距离增加，不同弹性模量的介质的振动幅值会很接近，甚至会出现高弹性模量介质的振动幅值更大的情况，如爆源距离30 m处，弹性模量为10 GPa的介质的速度幅值为0.85 cm/s，而弹性模量为15 GPa 的介质的速度幅值为0.90 cm/s。

然后，研究黏性系数对介质吸收能力的影响，数值积分中取弹性模量E=20 GPa，黏性系数分别为η=5、10、15、20 MPa·s，其余参数同前，计算结果如图13和图14所示。

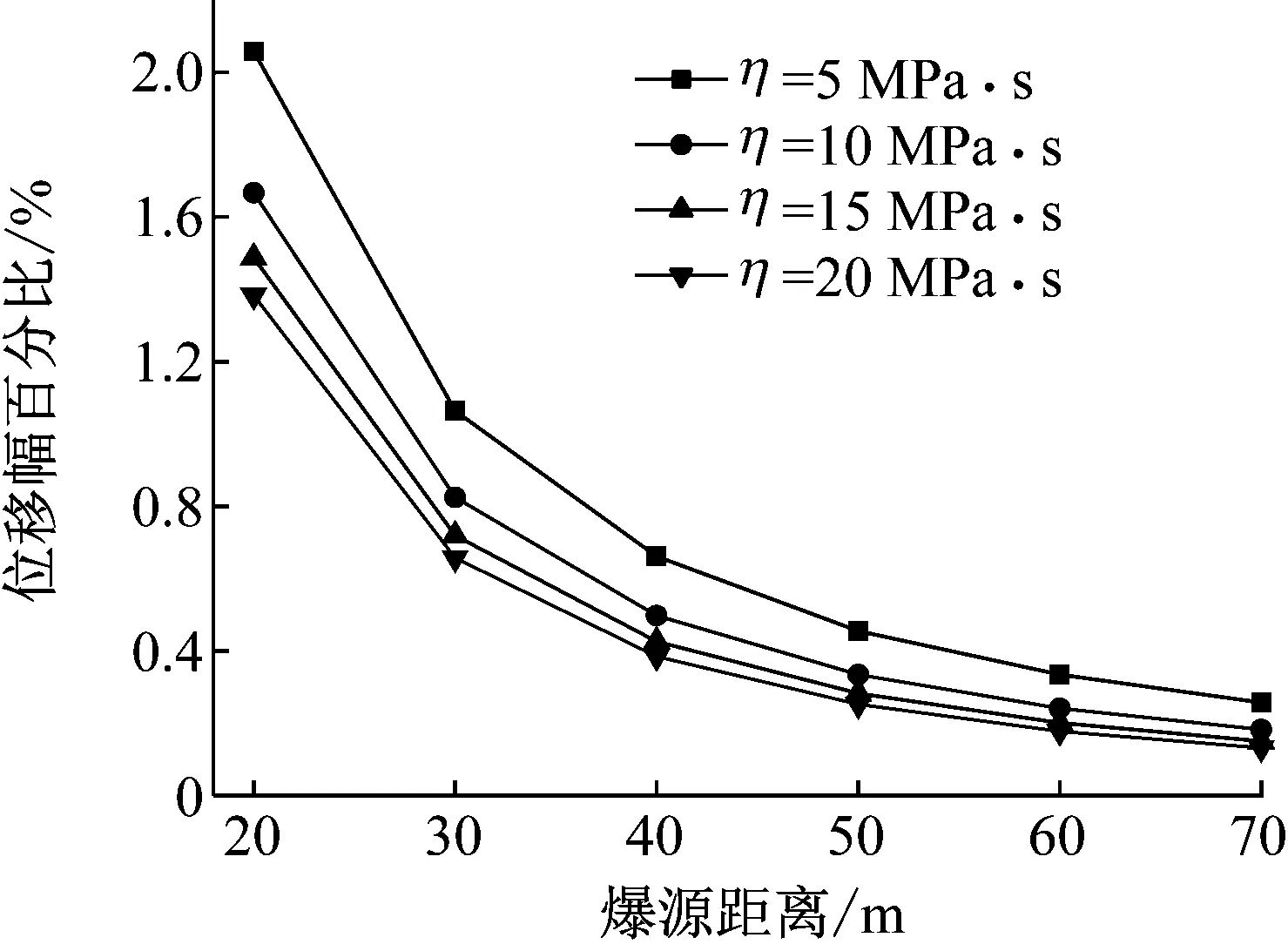
图13 位移幅值百分比与爆源距离的关系Fig.13 The relationship between the displacement amplitude percentage and the source distance

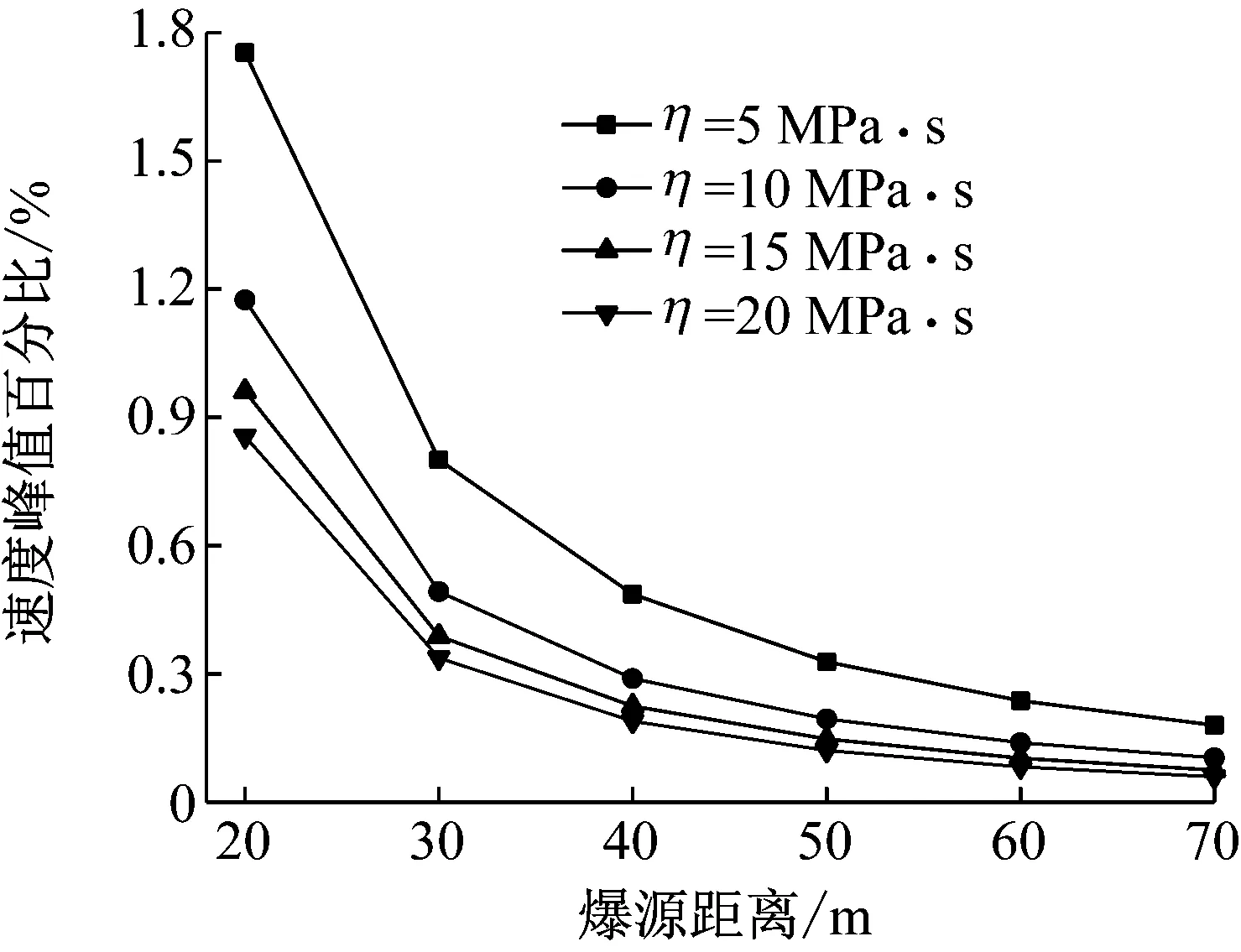
图14 速度幅值与爆源距离的关系Fig.14 The relationship between the velocity amplitude percentage and the source distance

由图13和14可知，介质的黏性系数越大，介质对爆破地震波的吸收能力越强。结合上述弹性模量对介质吸收能力影响的结论，可知介质的黏性系数与弹性模量的比值越高，介质对爆破地震波的吸收能力越强。

最后，采用归一化的振幅频谱描述在不同黏性系数的介质中，质点速度频谱随爆破地震波传播的变化规律。数值积分中取弹性模量E=20 GPa，黏性系数分别为η=0、1、5、10 MPa·s，其余参数选取同前，计算结果如图15(a)、(b)、(c)、(d)所示。

由图15(a)可知，当黏性系数η=0 MPa·s，即介质为弹性材料时，爆破地震波的频率成分在爆源距离达到20 m后几乎不发生改变，这与上述定义爆破扰动远区的位置相同。当考虑介质的黏性时，随传播距离增加，爆破地震波高频成分相对于低频成分减小，黏性系数越大这种减小的速度也越快，如图15(b)、(c)、(d)所示。

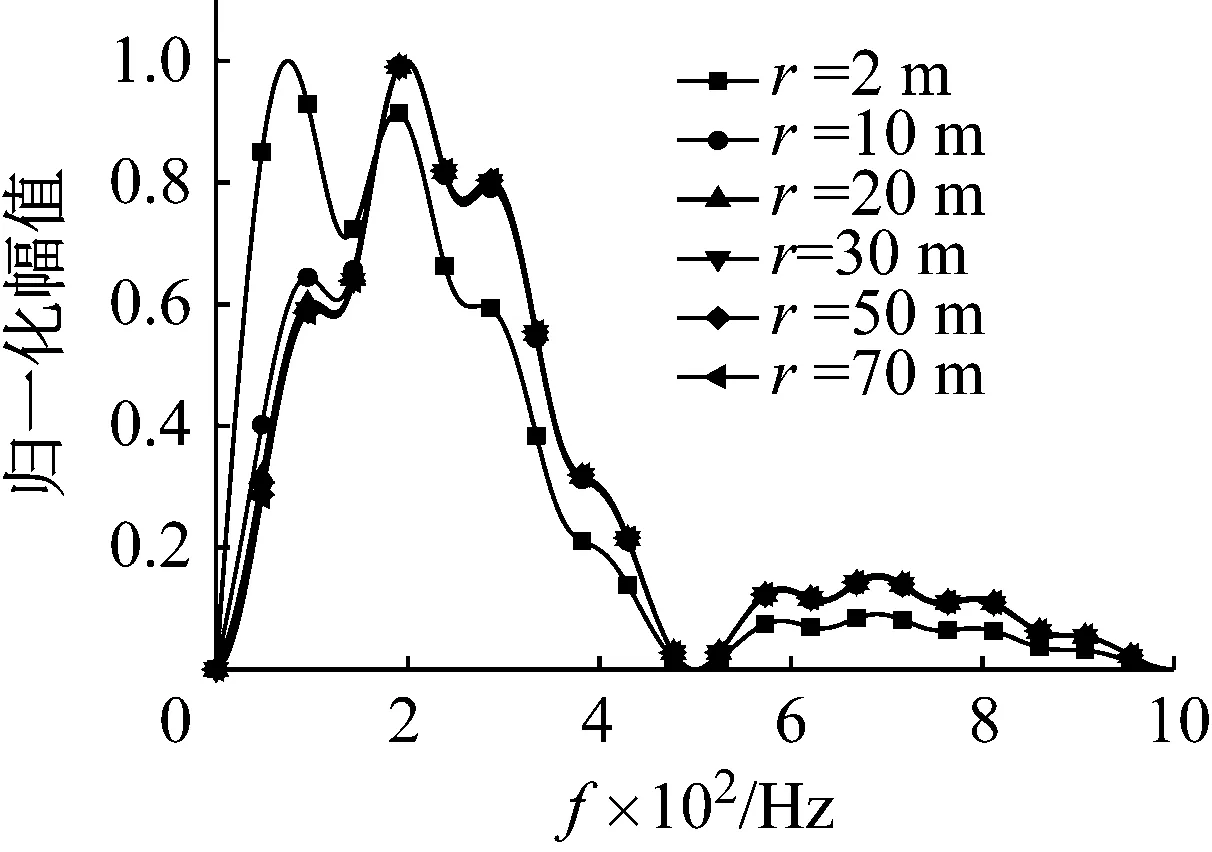
(a) η=0 MPa·s

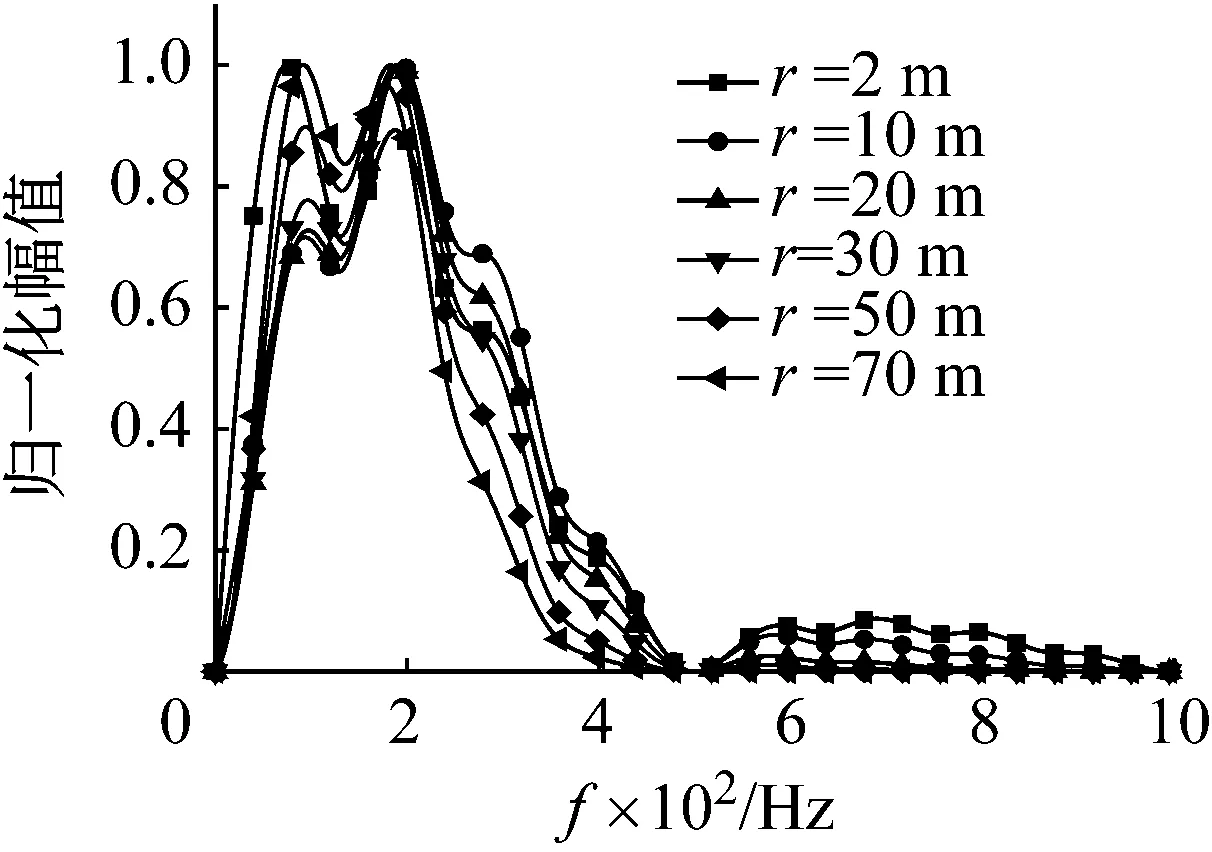
(b) η=1 MPa·s

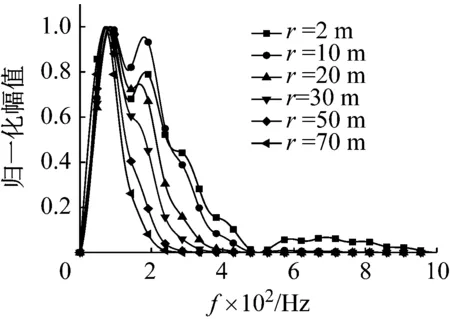
(c) η=5 MPa·s

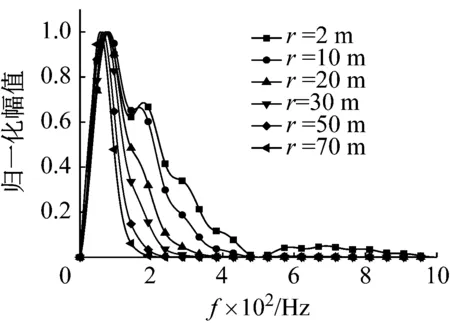
(d) η=10 MPa·s图15 不同爆源距离的质点速度频谱Fig.15 Particle velocity spectrum for different source distance

4 结 论

本文将岩体考虑成Kelvin-Voigt介质，并将爆破荷载等效地施加在爆破震动区边界上，通过傅里叶变换得到爆破地震波的积分解，经过数值积分和参数分析，得到如下结论：

(1) 爆破荷载上升时间越短，震动区边界的振动幅值越大；爆破荷载总持续时间越长，震动区边界的振动持续时间也越长，但振动幅值几乎不受影响。

(2) 在相同爆破荷载作用下，随介质的弹性模量增加，震动区边界的振动幅值减小，振动持续时间略微减短；在相同爆破荷载作用下，随介质的黏性系数增加，震动区边界的振动幅值减小，振动持续时间略微增长。

(3) 爆破地震波在介质中传播存在波阵面的几何衰减和介质吸收的衰减，几何衰减分为近区衰减和远区衰减，在近区的衰减速率大于1/r，在远区的衰减速率等于1/r。介质的黏性系数与弹性模量的比值越高，介质对爆破地震波的吸收衰减能力越强。

(4) 爆破地震波在弹性介质的传播过程中，其频率成分只在爆破扰动近区产生变化，传播到爆破扰动远区后频率成分不发生改变；爆破地震波在黏弹性介质的传播过程中，随传播距离增加，其高频成分相对低频成分不断地减小，且介质黏性系数越大，减小的速度越快。