迭代学习控制策略在连铸结晶器振动系统中的应用
章家岩, 孟庆喜, 冯旭刚, 沈 浩, 王 兵, 胡雪峰
(1. 安徽工业大学 电气与信息工程学院,马鞍山 243002;2.安徽工业大学 电力电子与运动控制省高校重点实验室,马鞍山 243002)
连铸生产具有操作灵活高效、成本低、产品品质好等众多特点,被广泛应用于各国钢铁企业。结晶器振动技术是连铸生产工艺的核心所在,其控制效果好坏直接影响产品质量。结晶器振动装置是连铸机的振动机构,其作用是防止钢坯与结晶器黏连,以得到合格的铸坯表面,因此对结晶器振动的控制十分重要。
结晶器振动技术一般可以归纳为同步振动、负滑脱振动、正弦振动以及非正弦振动[1]。同步振动具有很好的脱模效果,但主要靠凸轮实现,对机械寿命、铸坯质量有很大影响。负滑脱振动相比同步振动保证了结晶器运动的平稳性,但也由凸轮机构实现振动,具有和同步振动同样的缺点。正弦振动克服了以上两种振动方式的缺点,过度过程平稳、冲击小、振动频率高,是目前国内外连铸生产中应用最广泛的一种振动方式。近年来,连铸坯热送直接轧制技术的发展和拉坯速度的不断提高对连铸坯的表面质量提出了更高的要求。为解决高振频、高拉速引发的漏钢问题,结晶器下降时间比上升时间短的非正弦振动形式由于突破了传统正弦振动的限制,已逐渐成为一项发展成熟并被应用于连铸生产的新技术[2]。目前,主要通过基于电液伺服的液压振动装置实现结晶器非正弦振动[3]。已知的对于结晶器振动控制技术的研究主要集中在以下三个方面:①前馈扰动补偿优化控制模型设计,如文献[4]根据两缸实际振动位移的偏差,设计同步控制方案及算法,对两缸各自的给定量或控制量进行修正,以保证两缸同步协调工作,减少振动偏差。同时针对摩擦力和重力对振动控制系统动态和静态特性的影响,以及在位置控制伺服系统中具有压力反馈时对系统的不稳定性作用,采用基于经验的摩擦辨识方法和非线性摩擦观测器,建立动态摩擦补偿方案,以消除这些外力因素造成的振动不稳定影响。但这些前馈控制方案由于其开环控制和局部扰动补偿特点,难以满足动态控制要求,并且大部分场合扰动量难以测量,只能采用经验模型进行估算,因此目前基本停留在仿真研究阶段,无法在实践中加以应用。②基于反馈控制的PID或改进PID控制方法。如文献[5-6]分别采用变参数PID和自整定模糊PID控制方法应用到电液伺服驱动的连铸结晶器振动控制系统,应用AMESim/Simulink联合仿真手段,建立振动系统模型和控制系统模型,进行系统仿真研究。但由于该系统具有的特殊性,工况改变也会使负载和被控系统的特性跟踪改变,致使系统的非线性和不确定性增加,难以建立较准确的数学模型。因此,对PID控制进行改进的方法显然也难以保证系统在工况变化情况下的动态性能。③基于反馈控制的先进控制算法。如文献[7]针对电液伺服角振动台性能的需求进行实验室环境下的振动模拟试验,提出并应用复合迭代非线性控制方法,分析了其收敛条件,实验和仿真对比表面此控制策略对模拟实验设备电液伺服角振动台振动信号具有较好的实时控制效果。但这样的实验室环境下的模拟试验装置显然与工业现场运行的结晶器振动设备存在着较大的差别。
由于连铸结晶器振动系统复杂的工艺特点,及对生产连续性的要求,不能随意停产试验,因此即使PID控制方法存在上述许多缺点,工程上仍然采用它来设计控制器,通常调试工作是在生产线投产或改造时对整个控制系统进行统一调试,所以先进的控制方法难以投入应用。所以目前结晶器振动技术先进控制策略的文献研究发现甚少。为此,本文提出了一种由PID和迭代学习控制器构成的结晶器液压振动复合控制系统,对结晶器液压振动系统模型进行仿真实验以检验ILC算法的动态跟踪效果。在此基础上,以宝钢梅山炼钢厂2号连铸机为对象投入控制运行,达到了较好的实际应用效果。
1 控制系统分析与描述
1.1 系统结构
常用的液压振动机构有单液压缸驱动短臂四连杆式、双液压缸驱动的短臂四连杆式和垂直升降式,本文研究对象宝钢梅山炼钢厂2号连铸机结晶器振动机构所采用的是电液伺服阀控制的双液压缸垂直升降式导向板簧振动机构,相比于四连杆式振动机构具有寿命长、运动轨迹准确、振动冲击小和允许高频振动等优点。其液压振动装置主要由振动底座、液压振动缸、振动台、缓冲弹簧、导向板弹簧、液压动力系统组成。在液压系统的作用下,振动台受到液压缸的作用力,以期望的输入给定进行周期受迫振动,系统结构如图1所示。x为液压缸中的活塞位置,经位移传感器检测后输出电压信号uf,与给定ud进行比较得到偏差信号e,再由控制器对偏差信号e进行矫正,校正后将控制信号送入伺服放大器,将控制器输出信号以电流信号i施加给电液伺服阀,控制液压缸按给定信号规律运动,从而构建位置闭环控制系统。即通过控制算法使振动规律跟随计算机给定,从而使液压缸获得期望的振动规律。
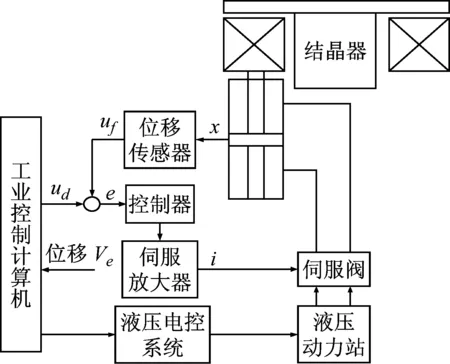
图1 结晶器电液伺服振动系统原理图Fig.1 Schematic diagram of electro-hydraulic servo oscillation system
1.2 特性分析
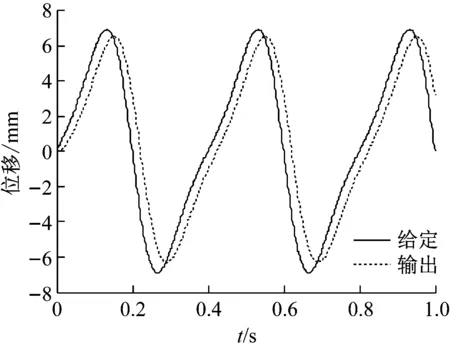
根据工艺要求,结晶器工作时需要按照设定的频率和振幅实现周期性的往复受迫振动。现代连铸结晶器大多采用液压伺服振动系统,它可以在拉速Vc变化很大时,较方便地在一定频率范围内在线调整所需的振动波形、频率和振幅,以满足连铸工艺的要求,而目前采用的非正弦电液伺服控制技术,则能更好地达到高拉速、高质量铸坯的目的。电液伺服控制系统是一种能以较高精度实现输出量快速、连续地跟踪输入信号变化的液压伺服系统,另外其控制和参量反馈容易实现,且具有较大的输出功率,在冶金、机械、化工等领域的自动控制系统中得到了广泛的应用[8]。然而,由于工业现场复杂环境的影响,被控对象模型的结构参数时常受外界干扰而发生变化和摄动,并且液压振动系统本身具有的非线性、不确定性现象非常严重,特别是在高压和重载的情况下这种现象更为突出,需要加以充分考虑。经过分析发现,影响结晶器振动控制系统的不确定性因素主要有:
①油源压力、流量脉动;②结晶器壁与铸坯表面的机械磨损和干摩擦力的变化,改变了负载原始特性,导致对象参数改变,影响控制效果;③位移传感器检测信号强度较弱,容易受到噪声和零漂的影响;④管道和油滚状态不同引起的液容和摩擦系数变化及有效容积改变;⑤阀的滞环、阈值和温度或压力引起的零点漂移;⑥电磁搅拌发出的磁性干扰;⑦拉坯速度的不稳定。
通过以上分析,本文针对结晶器振动控制系统提出的具体要求为:①使系统满足静态和动态性能要求,增加系统的快速性,减少超调量;②系统对非线性等不确定性影响具有很强的鲁棒性;③控制算法须有较强的实时性和自调节能力,且简单、可靠、易实施;④提高结晶器生产运行的可靠性。
2 控制方案设计
2.1 系统架构
结晶器振动是一个呈周期性的往复运动过程,这一性质比较适合采用迭代学习控制方案[9-10]。迭代学习控制可以高精度的跟踪给定,是一种重要且有效的智能控制方法,在工业应用中具有很好的控制效果。但迭代学习控制的主要问题之一是鲁棒性问题[11-14],由于连铸生产环境是不断变化的,动态参数存在各种不确定性、扰动和偏差,导致鲁棒性问题尤为突出。为了解决这一问题,本文在前向通道加入可靠性较高的控制器,以起到系统的镇定作用,并由此构建迭代学习复合控制的结晶器振动系统方案。基于迭代学习控制的结晶器振动系统架构如图2。
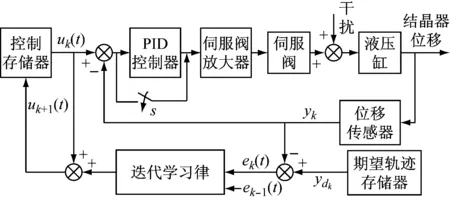
图2 迭代学习控制的结晶器振动系统结构图Fig.2 Structure chart of iterative learning control systems for mould oscillation
控制器由内部控制器环节和外部控制器环节构成。以传统的数字PID控制器作为内环控制器,可以提高系统的可靠性,达到镇定系统的作用。通过内环控制器环节,还可以提高系统的抗干扰性能,提高迭代学习的收敛速度。
2.2 控制器的设计
迭代学习控制的原理是反复利用系统的先前经验,根据系统输出反馈和给定目标轨迹偏差修正控制信号,用简单的学习算法得到一个理想输入,控制对象按照期望方式运动。根据系统偏差信号e,采用函数迭代学习机理不断修正系统的实际输入,构造一系列函数控制序列{uk(t)}收敛于一个可实现的控制信号ud(t),使得实际输出与期望输出间的误差达到满意,也即
(1)
有最优解的系统输出[20]。
控制器实现步骤
步骤1S闭合,进行迭代学习控制,控制器的输出直接进行伺服阀阀芯移动量控制。当k次迭代计算时,控制输出uk+1(t)通过引入前一次(k-1次)t时刻的控制输出uk(t)和位移误差量ek-1(t)=yd(t)-yk-1(t),及本次(k次)t时刻的位移误差ek(t)=yd(t)-yk(t),在不断的利用系统前次运行的信息和本次运行信息进行学习算法的计算,当在t∈(0,T)区间内实际输出与期望输出在精度要求范围之内时,存储本次运行数据,进入第二步控制过程。同时也在不断的进行迭代学习控制算法的计算和目标函数的计算。
步骤2S断开,进行迭代学习复合控制。应用迭代学习过程中当前存储的最佳过程数据进行最小二乘法数据拟合处理[19],得出PID控制参数,并代入算出的参数于PID控制器,实现迭代学习控制和PID复合控制方案。当结晶器振动位移发生小的偏移时,PID内环很快进行局部减少偏移量方向调节,而迭代学习控制器此时起到系统控制补偿量的作用。尽可能的保证振动控制器工作在步骤二的控制过程,保证系统的准确性和鲁棒性。
引入目标函数式(2)判定迭代学习是否达到精度要求,一旦达到控制精度要求,即当J<ε时,存储产生本次结果的迭代学习控制量uk(t)和输出位移量yk(t),并启动复合控制方案。当在某个周期内目标函数超出了控制精度要求时,即当J>ε时,再次以步骤一运行,进行控制参数寻优的过程。即目标函数为
其中ek(t)=yd(t)-yk(t)
(2)
若在[0,T]的采样时间内的采样点数为M个,有
U(t)=[u(0),u(1),u(2),…,u(M)]T
(3)
Y(t)=[y(0),y(1),y(2),…,y(M)]T
(4)
Er(t)=U(t)-Y(t)=
[er(0),er(1),er(2),…,er(M)]T
(5)
式(3)、式(4)和式(5)中,U(t)和Y(t)为uk(t)和yk(t)的M个采样点构成的迭代学习控制输出向量和结晶器振动位移输出向量,Er(t)和Yd(t)为控制偏差和期望输出的M个采样点构成的向量。
令kp、ki、kd为线性PID控制器的基本参数,由式
(6)
根据式(6),采用最小二乘法拟合处理计算出PID控制器的参数。最后将常规PID控制参数修改为拟合后的参数值,构成自学习式的参数整定控制系统。
3 电液系统设计及仿真分析
3.1 负载计算与设备选型
在实际应用中,本文针对梅钢炼钢厂2#高拉速板坯连铸机结晶器液压振动设备,根据负载特性进行有关参数的选取。由工艺要求可知,液压缸振动按非正弦规律运动,即液压缸位移为
x=xmsin[wt-αsin(wt)]
(7)
则液压缸的速度变化规律分别为
(8)
式中:α为波形偏斜率;xm为最大位移;w=2πf频率。梅钢2号连铸机结晶器液压振动装置的技术参数范围为:偏斜率α∈[0.3,0.7];振动频率f∈[0,400]c/min;振幅x∈[0,12]mm。根据工艺要求取α=0.6;xm=6.9 mm;f=152 cpm
(counts per minute)。
设结晶器端有重力负载、惯性负载、干摩擦负载和黏性摩擦负载,折算到液压缸端最大负载时液压缸端负载力为Fm=20.16 kN。现场供油压力Ps=16 MPa,取液压缸最大负载压力为2Ps/3以得到液压动力元件能与负载的最佳匹配。液压缸作用面积为A=18.9×10-4m2,考虑漏油等20%的裕量影响,则供油流量为29.93 L/min,故阀口总压降为5.33 MPa。最大压力28 MPa,额定电流20 mA,阀压降为7 MPa时额定流量为40 L/min,放大器增益Ka=0.008 07 A/V。从而伺服阀静态流量增益为Ksv=50.4×10-3m3/(s·A),频率wsv=571.2 rad/s,阻尼比ζsv=0.7;液压动力缸频率为wh=263 rad/s,阻尼比为ζh=0.2。位移传感器采用MTS公司的RH型线性位移传感器,增益为Kf=200 v/m。
考虑文献[15-16]建立结晶器振动系统模型,忽略一些次要因素,并做以下理想化处理:
①控制阀为理想的比例伺服阀,忽略节流窗口外的紊流流体在阀中的压性能;②阀具有理想的动态响应能力,即流量能随阀芯位移和阀压降的变化瞬间进行相应改变;③供油压力为固定值保持不变,回油压力为零;④所有管道短而粗,忽略摩擦损失、管道动态及流体质量影响。
由此可得到结晶器电液位置伺服系统的数学模型如下
(9)
式中:Ks=KaKfKsv/A
wsv为伺服阀的固有频率;wh为液压固有频率;Ksv为伺服阀的静态流量增益;Ka为放大器增益;Kf为位移传感器增益;ζsv为伺服阀的阻尼比;ζh为液压阻尼比;A为活塞有效面积。
3.2 计算机仿真
迭代学习控制原理图,如图3所示。

图3 迭代学习控制原理Fig.3 Iterative learning control principle
Uk+1(t)为系统第k+1次学习输入,Uk(t)为系统第k次学习输入,Vk(t)为系统第k次输入,Yk(t)为系统第k次学习输出,Ek(t)为第k次输出偏差,其中k为学习次数;G为系统传递函数;H为反馈环节;Yd(t)为系统期望输出;F为学习环节,由图3得
Yk(t)=G×Vk(t),
Ek(t)=Yd(t)-Yk(t),
Vk(t)=Uk(t)+H×Ek(t),
Uk+1(t)=Uk(t)+F×Ek(t)
(10)
对于SISO系统,可取F=H,则可以推导出Ek+1(t)=|1/(I+GH)|Ek(t),令收敛半径ρ=|1/(I+GH)|。可以看出当ρ<1时,误差Ek(t)收敛。G为传递函数,通常不会改变,所以该算法就转化为了构造H的问题,使之满足:①(I+GH)是正定的,I为单位矩阵;②(I+GH)-1是渐近稳定的;③ρ=|1/(I+GH)|<1。显然针对式(9)的电液位置伺服控制系统,取F=H=KfS,满足条件①和②,对于③有
ρ=|1/(1+GH)|=
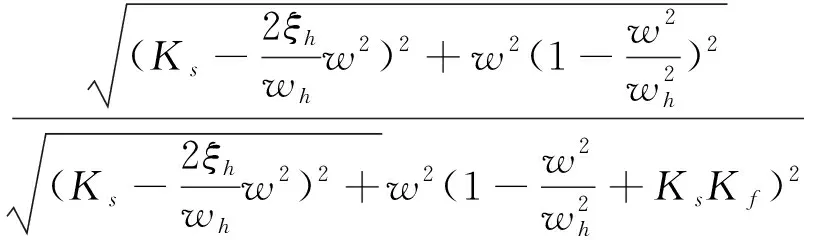
(11)
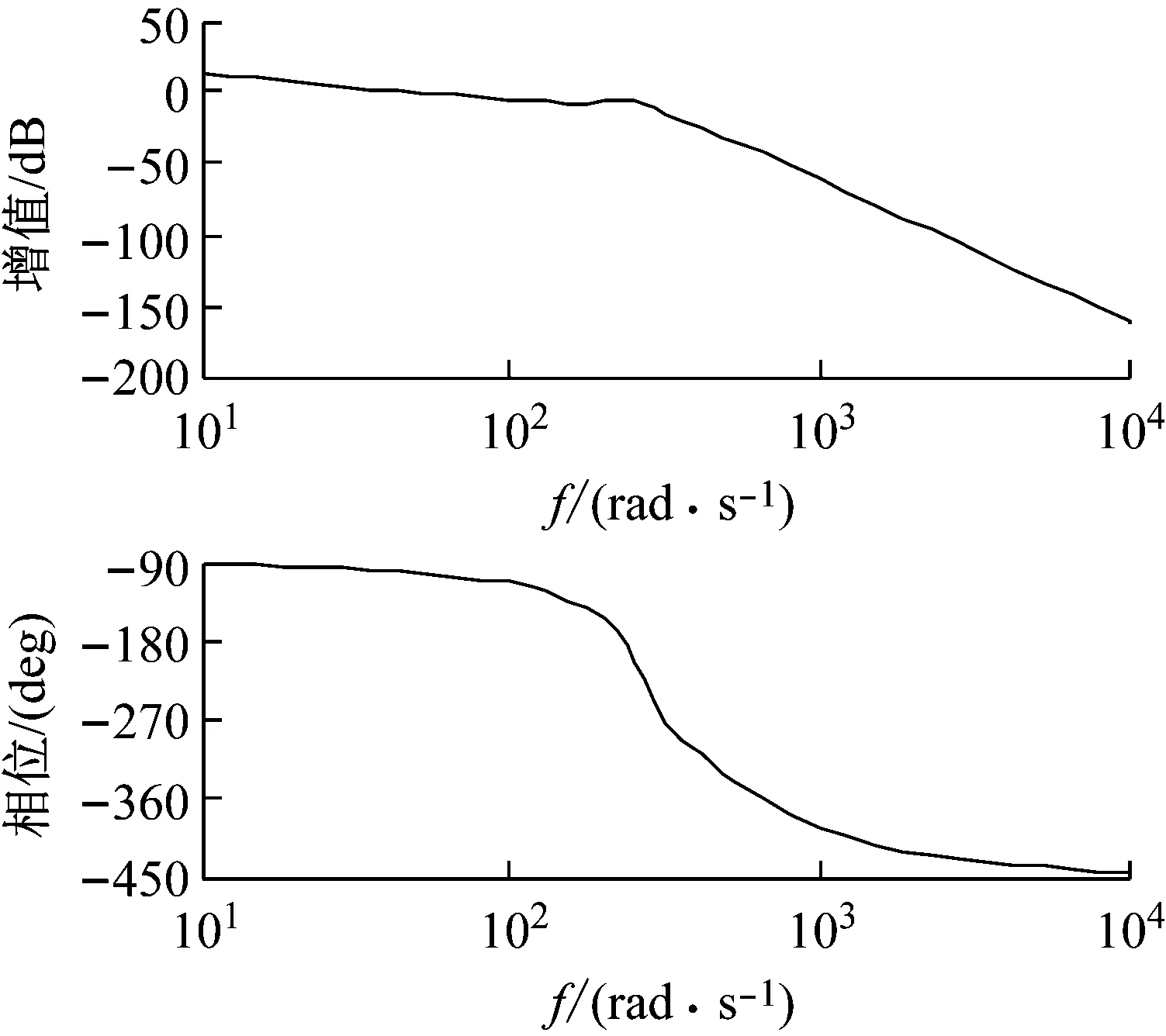
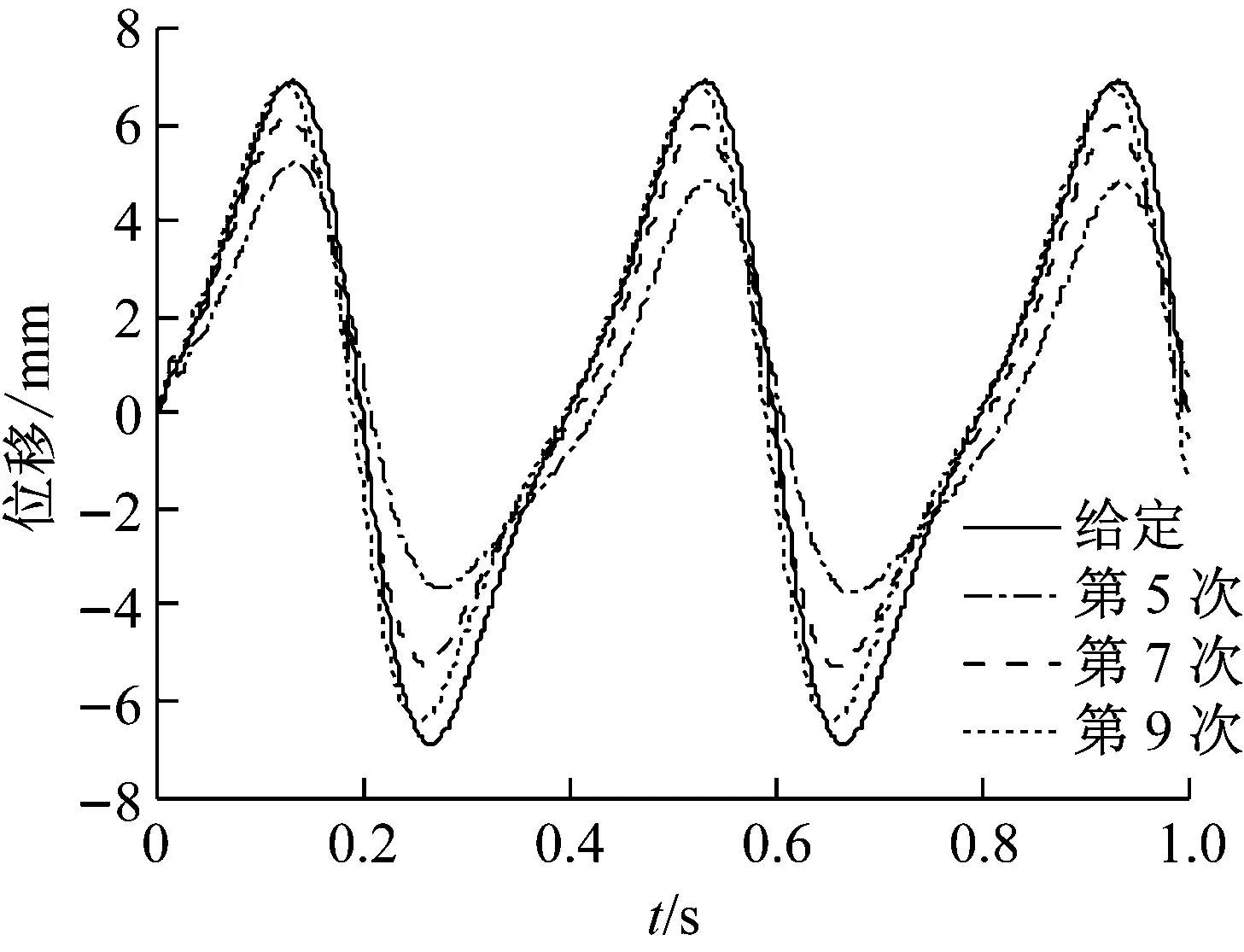
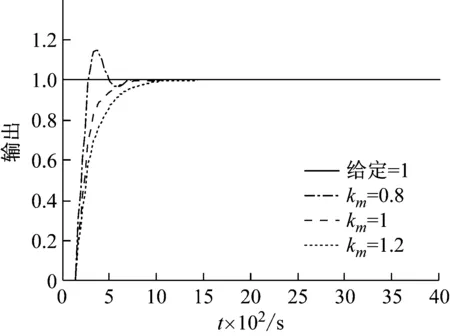
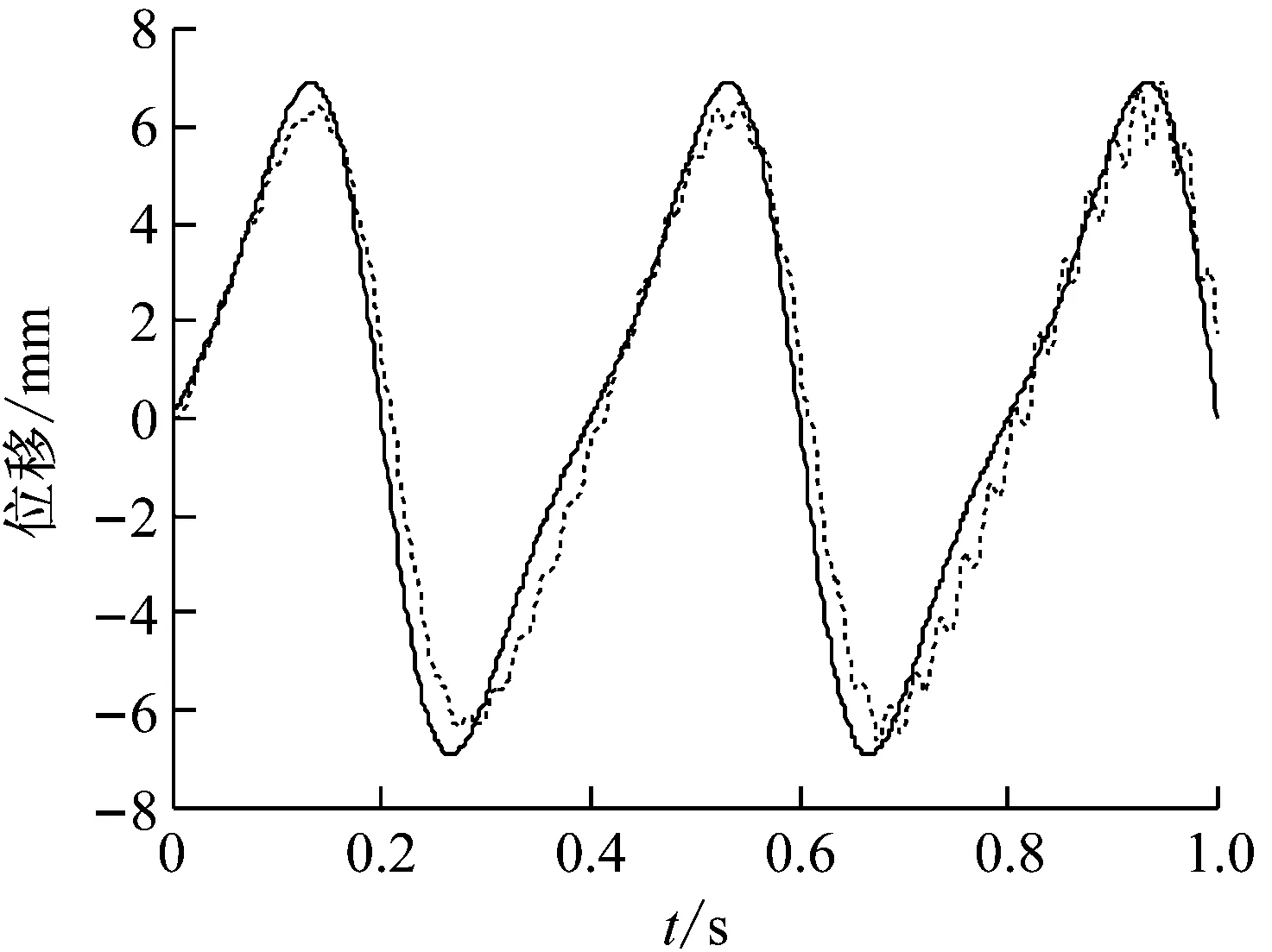
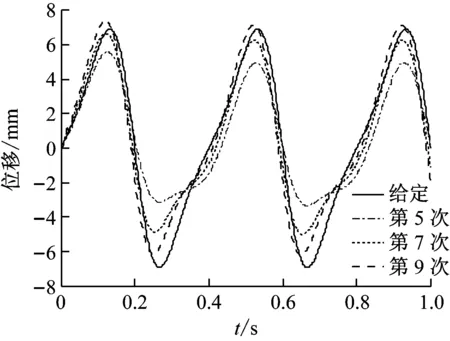
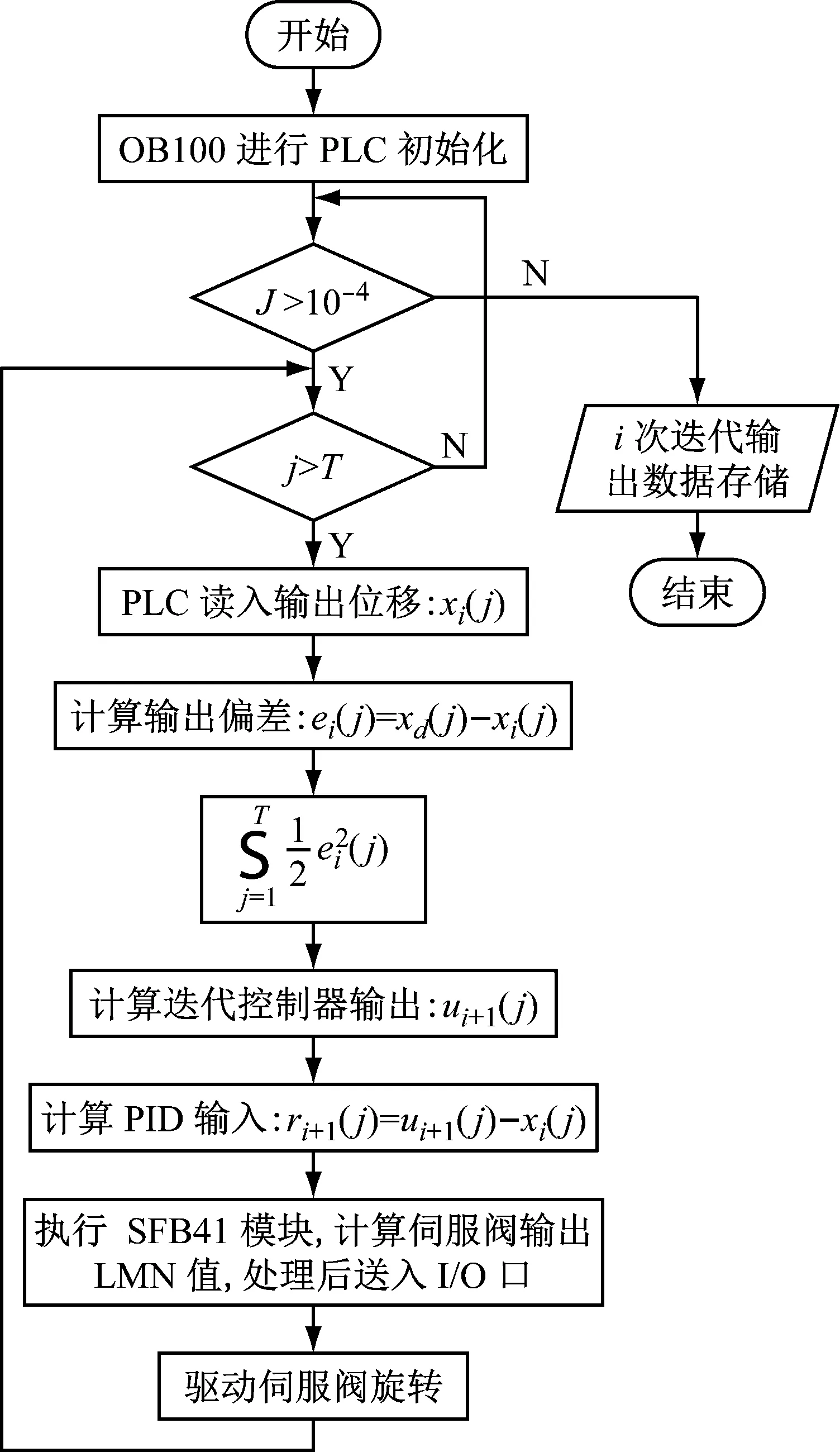
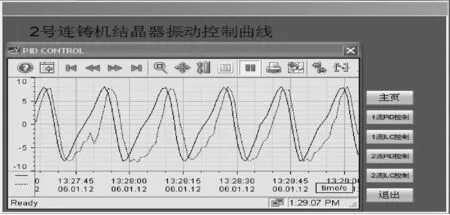
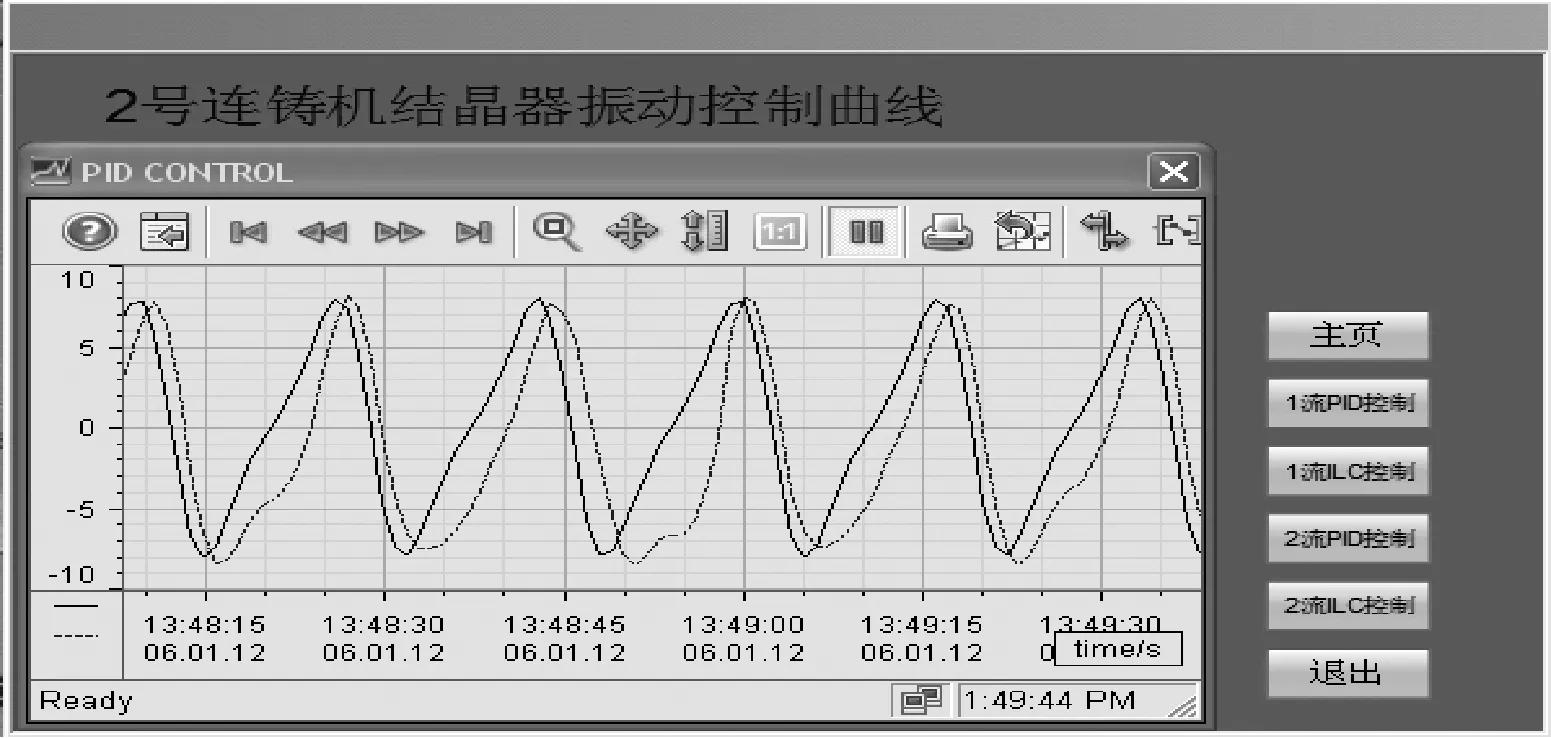
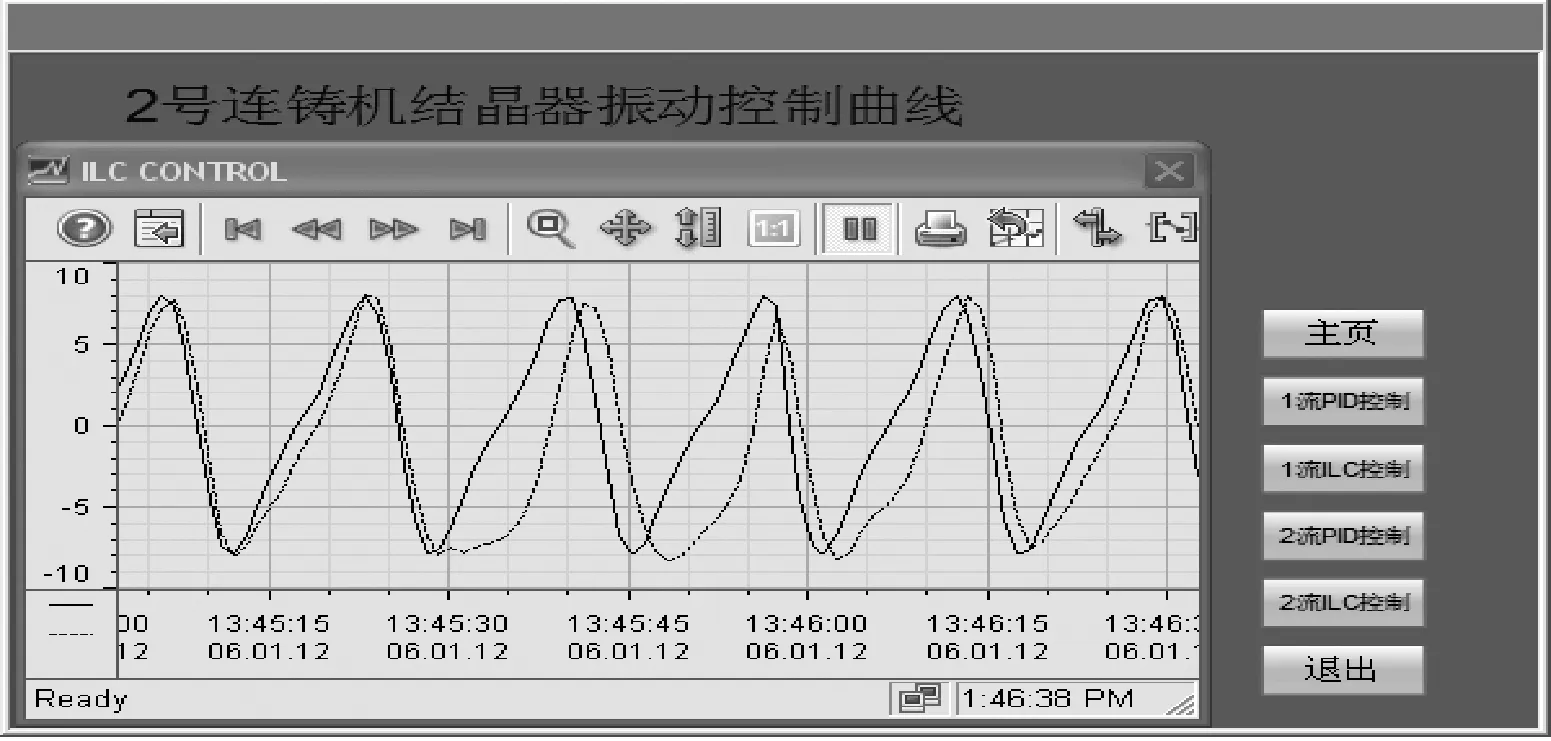
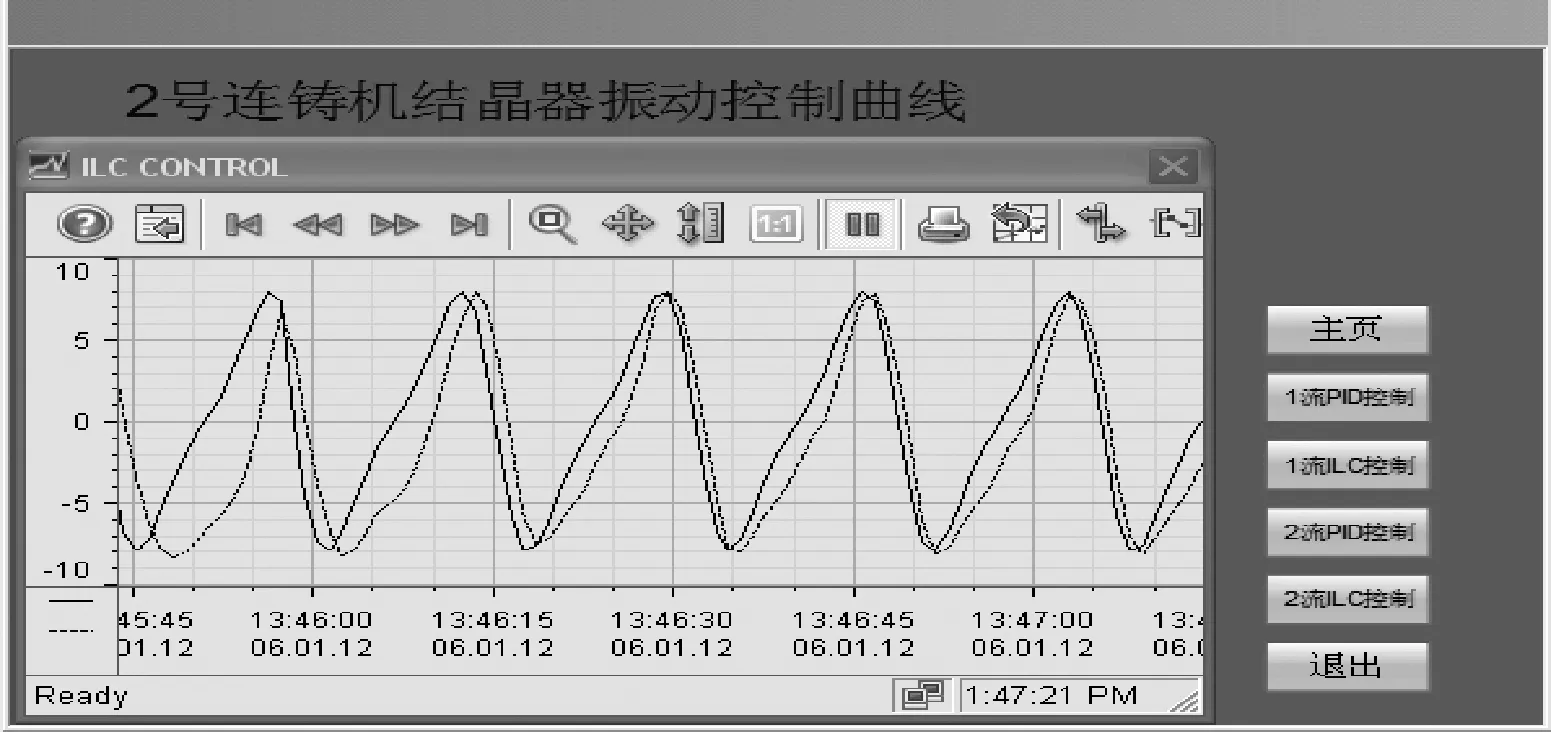
由于系统的输入信号频率w< 将上述参数代入并用MATLAB进行模型转换处理得到状态空间模型 (12) (13) 首先,用MATLAB对系统的幅频和相频特性进行稳定性分析,作结晶器系统幅频相频波特图曲线,如图4所示。 图4 结晶器系统幅频相频波特图曲线Fig.4 The amplitude frequency and phase frequency characteristic curve of mould system 分析图4可知,穿越频率wc=44.2 rad/s,相位裕量γ=79.8°;相频穿越-180°时,wg=230 rad/s,幅值裕量为Kg(dB)=7.14 dB。以上参数完全满足系统的稳定性要求,故而满足迭代学习控制的要求。但穿越频率wc很小时,系统的动态性能较差,跟踪曲线精度不理想。采用传统PID方法进行控制时,控制器参数根据Z-N法[17]确定,增益参数kp=10、ki=2.5s、kd=0.4 s。MATLAB的仿真结果,如图5和图6所示。 图5 传统PID控制器输出Fig.5 Traditional PID controller output 图6 迭代学习控制仿真输出Fig.6 Simulation output of iterative learning control 由图5和图6可知,系统输出能够跟随输入信号,但是存在大约0.8 mm相位滞后,达不到系统的波形完全跟踪的精度要求,因此引进迭代学习先进控制算法。 连铸振动系统的参数摄动主要由伺服放大器、阀门流量增益和位移传感器增益的不确定性引起,故为验证本文设计控制策略的有效性,将以上参数摄动集中作为开环增益Km的参数摄动,对控制系统进行不确定性仿真。故含有参数摄动的实际被控对象表现为如下形式 (20) 式中:Ku为均匀分布的独立随机变量;本文选取Ku的摄动区间为[-p,+p],通常假定伺服放大器Ka、阀门流量增益Ksv和位移传感器增益Kf各具有最大±10%的不确定性,以随机摄动方式引用到系统模型[21]。由于Km=KaKfKsv/A,得到含有参数摄动的开环增益 (21) 其中: 对上式进行编程仿真,取t′,t″,t‴为[0,1]之间的独立随机变量,仿真结果如图7所示。 图7 开环增益Km的参数摄动Fig.7 Parameter perturbation of open loop gain Km 从图7可知,Ku的摄动区间为[-0.186,0.195],因此取p=0.2,分别取对象摄动为Ku=+0.2,Ku=0,Ku=-0.2三种情况。然后用单位阶跃作为输入,对系统振动的动态性能进行仿真。仿真结果,如图8所示。 图8 系统摄动仿真曲线Fig.8 Simulation curve of system perturbation 由仿真曲线分析可知,当Km减小时系统超调量增大,但响应速度加快;当Km增大时跟踪响应速度变慢,调节时间增加;但无论Km在摄动区间内如何变化,最终都可在较短时间内趋于稳态。因此,本文设计的迭代学习复合控制策略能够在系统存在一定不确定性的环境下保持良好的动态性能和鲁棒性。 为了进一步验证控制系统的动态跟踪能力,选取迭代学习开环增益Li=0.02、Lp=0.08、Ld=0.06;闭环增益Ti=0.05 s、Tp=0.05、Td=0.02 s。将采样时间设置为1 ms,误差精度要求为10-4,使用MATLAB 7.1对迭代学习控制器进行仿真,当迭代到第9次时满足系统精度要求,通过将第9次迭代的存储数据用最小二乘法进行拟合,计算得出PID参数kp=2.17、ki=4.13 s、kd=0.04 s,将以上参数代入PID控制器进行复合控制,仿真结果如图6所示,仿真结果表明,振幅误差减小到0.1 mm以内,静态误差明显减小,曲线基本与给定曲线重合,满足了系统对波形完全跟踪的要求。 在浇注过程中,由于干扰所带来的系统给定曲线偏离,一方面会减少负滑脱时间,影响钢坯表面质量,另一方面会减少润滑剂的消耗量,导致拉漏的危险。因此,为了验证控制算法抗干扰性能,在控制器的输出叠加小信号。图9为加入扰动信号fd=f0sin(10πt)时的PID控制输出曲线和迭代学习复合控制输出曲线。由图9可知,常规PID的输出有明显的振荡,表现较弱的抑制干扰能力,甚至会出现不稳定。采用迭代学习控制,经过几个周期的迭代学习控制后,系统中的干扰基本被消除,继续维持较好的稳定状态。对于抑制现场恶劣环境的一些不确定因素,迭代学习控制算法表现很大优势。 宝钢梅山炼钢厂2#连铸结晶器振动系统的控制平台结构上分为两级计算机系统,一是基础自动化级(L1),主要由西门子S7-300 PLC和C7-636 PLC作等过程控制器构成。二是负责生产过程控制的计算机级(L2),主要由数据总线与PLC、DCS等各控制器有机联接构成,实现分散控制和集中操作显示。S7-300作为主控制器(MCS),MCS通过MPI总线与铸流控制器(SC)C7-636联接进行数据传输,铸流控制器单独控制每流的伺服控制阀;通过MCS将振动控制参数(C1-C6)传送给SC,SC根据拉坯速度及参数C1-C6计算出非正弦系数、振频和振幅的设定值;油缸的位置信号由高精度位置传感器检测经ESIRON 4-20 mA转换器转化为模拟信号,传送给铸流控制器SC,经SC与给定信号比对计算出给定误差值,每隔1 ms传送液压系统构成闭环控制。当SC启动时,启动模块OB100对系统数据进行初始化计算;中断模块OB35每隔1 ms调用FB41实现PID控制功能,并在内部调用FB10模块(DB10背景数据块)进行误差求和计算,用以迭代程序软启动。用Step7中的SCL语言编程实现迭代控制功能,FC10根据给定参数计算给定曲线,图10为PLC迭代学习控制部分程序流程图。上位机程序对振动控制参数C1-C6在线可调,并实时监视结晶器振动曲线的振动幅值和频率。图11和图12为截取的2#连铸结晶控制器启动阶段和稳定运行阶段的部分监控曲线。由图11和图12曲线可知,PID控制启动快,但相位滞后明显,抗干扰能力弱,有明显振荡,甚至在曲线生成中存在严重变形现象,虽然短期就能达到稳定状态,但从图11(a)曲线和图11(b)曲线可以看出输出与给定仍有较大偏差,而且随着时间推移,曲线无明显重合趋势;而采用本文设计的迭代学习复合控制策略的控制系统虽然在启动初期输出曲线有严重变形,但基本能够在约7个周期后使输出与给定重合。从图12(b)中可以看出,输出与给定的相位滞后约为175 ms,幅值误差小于0.1 mm,但这些并未对结晶器负滑脱时间的减少产生影响,系统振动输出基本跟踪期望给定,控制效果明显;在结晶器振动系统的实际工作中,通常会在给定信号中叠加小幅抖振信号以防止伺服阀陷入死区(如上述正弦扰动信号),但引入小幅抖振信号也会使这种爬行振动方式的系统出现不稳定现象,因此也需要具有加强的抗干扰能力。本系统于2013年12月投入梅钢2#连铸结晶器振动控制系统运行至今,实现了在相同条件下比改进前提高拉速0.4 m/min,平均每月减少漏钢1次、增加作业时间180 min、提高铸坯产量500 t。从应用数据来看,本文设计的迭代学习复合控制策略使系统表现出来较强的干扰抑制能力,具有很好的控制效果。 (a) 加入扰动信号PID控制输出 (b) 加入扰动信号迭代学习控制输出图9 PID控制与迭代学习控制的输出比较Fig.9 Output comparison of PID control and iterative learning control 图10 程序流程图Fig.10 Program flow chart (a) PID控制输出曲线启动阶段监控画面 (b) PID控制输出曲线稳定阶段监控画面图11 PID控制输出曲线监控画面Fig.11 Monitoring screen about the output curve of PID control (a) 迭代学习控制输出曲线启动阶段监控画面 (b) 迭代学习控制输出曲线稳定阶段监控画面图12 迭代学习控制输出曲线监控画面Fig.12 Monitoring screen about the output curve of iterative learning control 通过分析连铸结晶器液压振动控制的生产现状。 (1) 阐述了控制系统的工艺要求以及影响液压位置控制的干扰因素,针对其被控对象具有非线性、时变和模型结构不确定性等特点,提出一种基于迭代学习控制策略的连铸结晶器液压振动系统复合控制解决方案。 (2) 用迭代学习控制算法的最优求解方法,选择合适的学习增益常数和初值并用MATLAB进行仿真分析。 (3) 阐述了该方案应用于宝钢梅山炼钢厂2#连铸结晶器振动控制系统的实现方法,比较分析了PID控制和迭代学习复合控制的控制效果。应用结果表明:迭代学习复合控制方法有效地提高了结晶器振动控制系统的跟踪精度,达到了较好的生产使用效果。
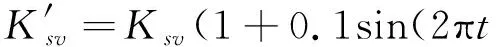

4 工程应用
5 结 论

