InSb薄膜热导率温度特性及传热机理
黄 正 兴, 孙 豪, 李 奇 松, 管 相 宇
(1.大连理工大学 电子信息与电气工程学部,辽宁 大连 116024;2.辽宁省集成电路技术重点实验室,辽宁 大连 116024;3.中国科学院上海光学精密机械研究所 高密度光存储实验室,上海 201800)
0 引 言
相变材料广泛应用于信息存储[1-3]、光热印刷[4-5]等技术中.对于数据存储,激光和电脉冲的相互作用使得相变材料薄膜在一个特定的结晶温度周围会发生晶态和非晶态的相变,信息位0和1的记录和读取是根据其晶态和非晶态下不同结构造成的不同反射率或者电阻率决定的[6].相变材料领域一直在探索新的功能,比如光子器件设备,具有超分辨结构的光学掩膜(可以减少光刻掩膜层的宽度和厚度),红外探测、成像装置以及热光刻设备等[7-9].在相变材料中,Ge-Sb-Te合金,比如 Ge2Sb2Te5、Ge1Sb2Te4、Ge1Sb4Te7[10-11],都是在实际应用中最常见的.其中典型的Ge2Sb2Te5材料已经有了多项应用,比如具有超分辨率结构的掩膜[12]、图像印刷技术等[13].
InSb(锑化铟)相变材料是近年来兴起的一种新型相变材料.InSb薄膜对1~5μm的波长敏感度高,此特性决定了其在红外探测领域的重要作用.早在1952年,窄禁带的相变材料InSb就已经被开发出来并逐渐开始广泛应用于红外探测器、红外雷达系统、红外热成像仪和红外天文学等[14].InSb在所有已知的化合物半导体材料中拥有最大的电子迁移率(78 000cm2/(V·s))和电子漂移速度(106m/s),因此,InSb在 Hall传感器件中也有广泛的应用[15-16].InSb还 被 用 来开发高速晶体管,并可降低功耗[17-18].此外,InSb薄膜用作具有超分辨掩膜层也具有非常大的应用潜力[19],其相应的超分辨光盘单层存储容量可达到50GB[20-22].上述应用无不说明了对InSb相变材料的研究具有重要意义.
在电子器件的实际应用中,器件内部不可避免地会产生热量,器件的散热、功耗等是影响器件性能和寿命的重要因素,而器件材料的热导率则对器件的散热和功耗有着重要的影响,因此材料随温度变化的热导率是决定器件性能的一个关键因素,也是检验材料是否合格的重要标准.需要通过实验对InSb相变材料热导率的温度特性进行测试,并且对其传热机理进行分析.过去几年,关于InSb材料的热特性有过几篇报告.Bhandari等研究了InSb体材料在室温下的热导率[23].Cai等研究了InSb体材料随温度变化的热导率[19].文献中测得的InSb体材料的热导率数量级普遍较大,室温下为11~12W/(m·K)[19].在上文中提到的实际应用中,无论是红外探测、信息存储还是超分辨结构掩膜层,InSb材料通常是微米级或者纳米级的薄膜材料.然而,InSb薄膜材料的热导率随温度的变化关系,包括晶态和非晶态,以及在非晶态转化为晶态的相变过程中的热导率变化却鲜有报道.本文工作旨在通过实验的方法获得晶态和非晶态InSb薄膜材料的热导率,尤其需要探索其随温度变化的函数关系.
1 实验原理
非晶态InSb薄膜,是在室温条件下使用射频磁控溅射仪,直接利用单合金靶材InSb在P型硅晶元上进行溅射沉积得到的.溅射过程在气压约为5×10-4Pa的充满氩气的密闭容器中进行,溅射压强为0.5Pa,溅射功率为40W,其沉积速率约为1nm/s.为了实验需要,准备了70、95、155、180和200nm 5个厚度的样品,分别用来进行厚度相关和温度相关的实验测试.晶态InSb薄膜则是在520K下,在真空环境中退火处理30min得到,退火前后的厚度可以视为不变.
热导率的测量是通过瞬态热反射方法来进行的[24-25].该方法是一种非接触式的无损光学方法,在对材料表面进行加热的同时可以得到其表面的温度变化.此外,样品制备和测量的实验装置都是简单易操作的,比较容易避免人为造成的实验误差.
测试系统的原理如图1所示,加热激光器是一种小型的脉冲激光器,其波长为1 064nm,脉冲宽度为8ns,单脉冲能量为50mJ,频率为1~20Hz.检测激光器是一个可发出连续激光的氦氖激光器,其波长为632nm,功率为1.8mW.加热激光可直射金属层表面,导致其温度增加,随着热量传导到薄膜层,其表面温度会随时间衰减,又由于金属的反射率对于其温度十分敏感,反射率在一个较宽而有限的温度范围内与温度基本呈线性关系[26],因此反射光强度曲线也可以反映温度的变化.快速光探测器的信号输出到示波器,示波器连接计算机就可以进行数据的拟合与分析.
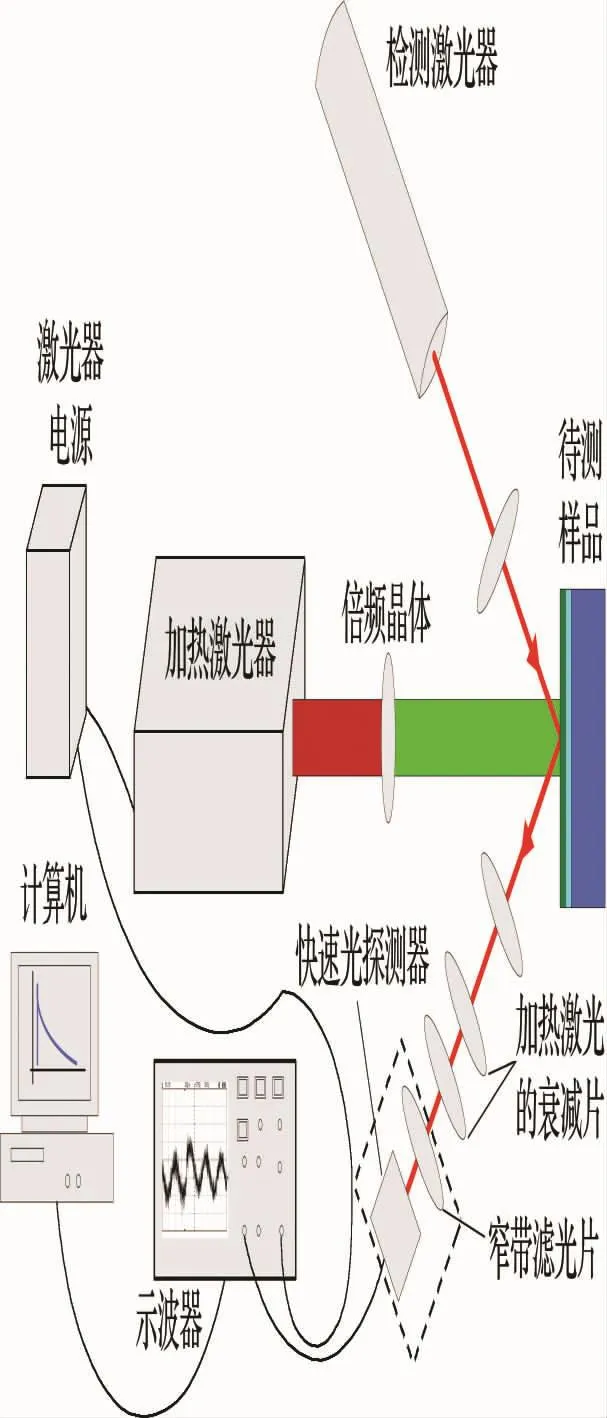
图1 瞬态热反射装置示意图Fig.1 Schematic of the transient thermo-reflectance setup
在拟合模型中,利用一维热传导方程来建立热传导理论模型,其中拟合过程使用了遗传算法[27-28].考虑到作为热阻层的薄膜厚度很小,可以使用双层传热模型进行拟合.
双层传热模型温度的拉普拉斯域表达式为[24]


式中:F(s)是关于f(t)的拉普拉斯变换公式,j是整数.使用室温下金属层和基底层的密度比热容和热导率数值:金属层使用金膜,其密度比热容为2.49×106J/(m3·K),热导率为317W/(m·K)[24];基底层为硅,其密度比热容为1.659×106J/(m3·K),热导率为148W/(m·K).归一化的温度衰减曲线很直观地反映了InSb薄膜样品的热扩散过程.数据拟合采用多参数优化的遗传算法[27-28].选取目标函数为

式中:Te(i)和Tt(i)分别为实验和理论的标准温度,Nr是随时间测量记录的次数编码.优化过程实际上就是求函数最小值的过程.
2 实验结果及讨论
图2、3分别展示了非晶态InSb薄膜归一化后的温度随时间的变化关系以及其热阻和热导率随厚度的变化关系.可以看出,总热阻随着厚度的增加而线性增加.界面热阻可以通过线性拟合得到.可以从图3拟合函数的截距得到非晶态的接触热阻为0.140 8×10-7m2·K·W-1.通过理论拟合,图3中的热导率k=(0.37±0.037)W/(m·K),其中±0.037为±10%实验误差,主要来源于样品厚度的测量.考虑到这个误差可能的影响,在图中也绘出了±10%误差的曲线.
图4、5则为晶态InSb薄膜归一化后的温度随时间的变化关系及其热阻和热导率随厚度的变化关系.其数据处理方法与非晶态InSb薄膜相同,拟合得到的接触热阻为 0.137 1×10-7m2·K·W-1,热 导 率 k= (0.55±0.055)W/(m·K),其中±0.055同样为±10%的实验误差.可以看出,晶态InSb薄膜的热导率比非晶态时增加了0.18W/(m·K).将在下文进一步分析其中的原因和机理.
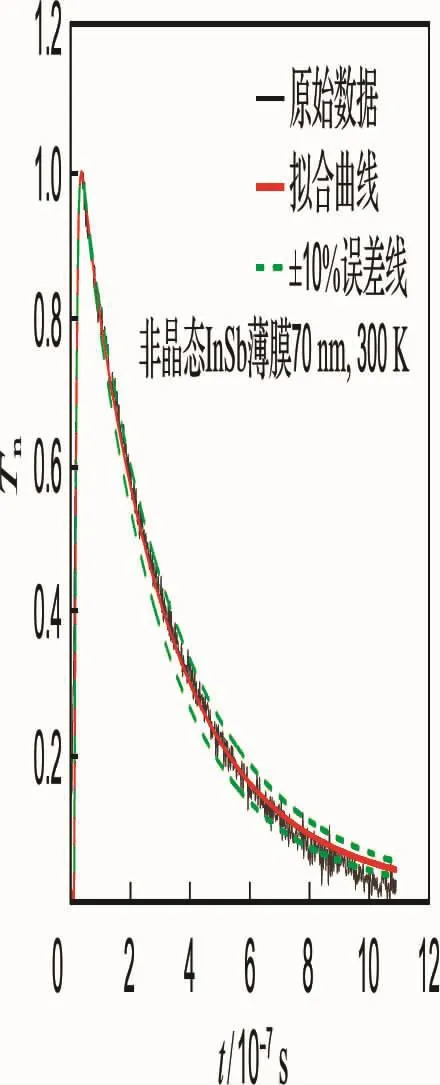
图2 非晶态InSb薄膜的温度衰减曲线Fig.2 The temperature decay curves of the amorphous InSb thin films

图3 非晶态InSb薄膜的热阻和热导率随薄膜厚度的变化曲线Fig.3 The thermal resistance and thermal conductivity curves of the amorphous InSb thin films along with the change of film thickness
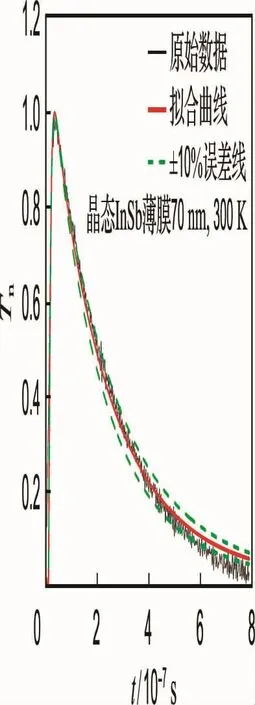
图4 晶态InSb薄膜的温度衰减曲线Fig.4 The temperature decay curves of the crystalline InSb thin films
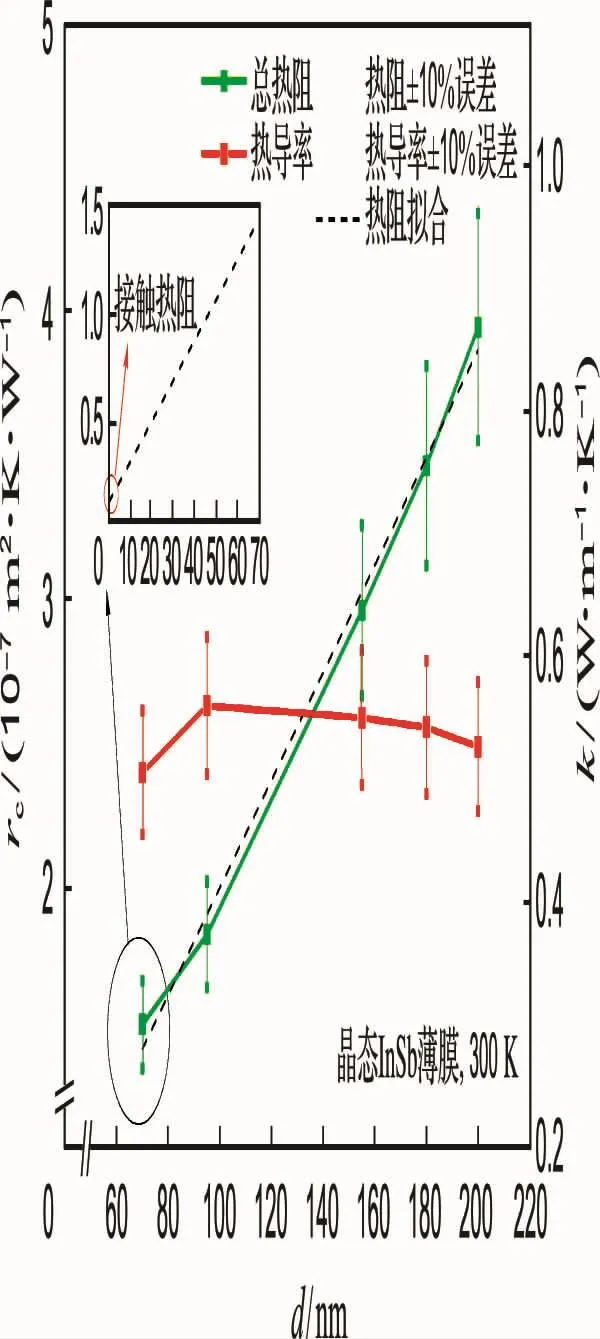
图5 晶态InSb薄膜的热阻和热导率随薄膜厚度的变化曲线Fig.5 The thermal resistance and thermal conductivity curves of the crystalline InSb thin films along with the change of film thickness
为了研究非晶态到晶态相变过程热导率的变化,测试了180nm的非晶态样品热导率随温度的变化关系.将样品固定在真空腔中,先后通过机械泵和分子泵将腔体内抽至压强小于5×10-5Pa的类真空状态;样品固定在一个由电流控制的加热台上,即可通过控制电流的大小来对样品进行温度控制.结果如图6所示.可以看出,对于非晶态InSb薄膜,当温度低于450K时,其热导率基本保持为0.37W/(m·K);当温度从450K升高到550K时,其热导率从0.37W/(m·K)突然升至0.55W/(m·K),说明此时样品已经结晶.而在温度从550K到300K的下降过程中,其热导率主要分布在0.57W/(m·K)至0.52W/(m·K)之间,随温度的减小略有下降.这表明非晶态InSb薄膜已经在控温测量过程中晶化.这个结果也可以由图7的XRD分析进一步证实.控温之前样品为非晶态,没有明显的衍射峰,而控温之后的XRD图出现了明显的衍射峰,说明已晶化.因此,可以认为控温测量的过程也是非晶态样品发生相变(结晶)的过程.图6还列出了文献[19]和[23]中测得的InSb体材料的热导率,可以看出,体材料与薄膜材料的热导率有很大的差异,这是薄膜材料的微观特性造成的,具体可从后续的理论分析看出.这也体现了对InSb薄膜热导率进行研究的重要性.

图6 非晶态InSb薄膜热导率随温度的变化曲线以及文献中InSb体材料热导率曲线[19,23]Fig.6 The temperature dependent thermal conductivity curve of the amorphous InSb thin films and the thermal conductivity curve of InSb body materials in the literatures[19,23]

图7 InSb样品分别在控温前和控温后的XRD衍射图谱Fig.7 The XRD diffraction pattern of InSb samples before and after the temperature control
3 理论分析
半导体晶体的导热一般包括电子导热、声子导热和光子导热,其热导率可以表达为

其中kph为声子热导率,ke为电子热导率,kr为光子热导率.对于纯金属而言,电子导热是主要机制;在合金和半导体中声子导热的作用逐渐增强;而在绝缘体内几乎只存在声子导热一种形式.光子导热只有在极高温度下才会有较大贡献,对于本文的测试条件则可以忽略[14].
根据 Wiedemann-Franz(W-F)定律[31],金属和半导体的电子热导率与其电导率相关.W-F定律表示如下:
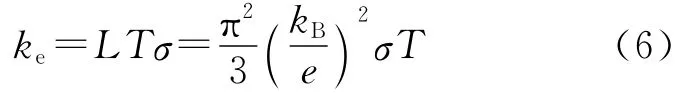
式中:ke为电子热导率,W/(m·K);σ为电导率,S/m;T为温度;L为Lorentz常数kB为玻尔兹曼常数,当温度大于Debye温度θD时,L=2.443×10-8W·Ω/K2[14].因此,电子热导率与样品的电导率和温度有关.
通过四探针方法测量了晶态和非晶态样品的电阻率,分别为8.47×10-5和2.7×10-2Ω·m,相应的电导率分别为1.18×104和37.1S/m.将电导率分别代入式(6)中可以得到晶态和非晶态样品电子热导率分别为0.09和2.72×10-4W/(m·K).与图6中的总热导率进行对比,可以发现,非晶态样品在450K以下温度时,其电子热导率对总热导率的贡献几乎可以忽略;在450K以上温度时,其总热导率增加了0.18W/(m·K).增加的热导率一部分由电子热导率提供(0.09 W/(m·K));另外,结晶后样品内部的晶格数增加,声子热导率也相应增加.至此可以认为,在非晶态下,InSb的热导率主要由声子导热提供,电子热导率几乎没有贡献;而在晶态下,电子热导率和声子热导率均对总热导率有一定的贡献.
声子热导率主要来源于晶体内声子气体的热传导,可以从分子动理论中获得[32]:

其中CV、v和lmfp分别为体积热容、平均声子速度以及声子平均自由程.在300~500K,可以假定CV和v不随温度变化.声子平均自由程的大小由声子与声子、电子、杂质原子和缺陷等的碰撞和散射决定.在理想的晶体中,高于Debye温度时平均声子数为[19]
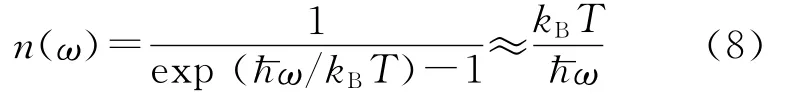
声子平均自由程与声子数成反比,而声子数与温度成正比,于是声子平均自由程也与温度成反比,从而声子热导率也与温度成反比,也就是kph∝1/T;而由式(6)可知电子热导率与温度成正比,也就是ke∝T.综合电子热导率和声子热导率与温度的不同依赖关系,晶态InSb薄膜的热导率随温度的变化应该不明显.这与图6中已晶化薄膜热导率的变化趋势相吻合.但是又发现,虽然晶态InSb薄膜热导率随温度变化不明显,但仍与温度呈微弱的正相关关系,这可能说明电子热导率受温度影响的程度比声子热导率大.另一方面,由于样品为纳米尺度的薄膜,W-F定律可能并不完全适用,由该定律计算得到的电子热导率可能存在一定偏差,这还有待进一步的研究.
4 结 语
采用瞬态热反射方法,测试了厚度为70~200nm的InSb薄膜在非晶态和晶态下的热导率.非晶态InSb薄膜的热导率为(0.37±0.037)W/(m·K),晶态InSb薄膜的热导率为(0.55±0.055)W/(m·K),它们都没有明显的厚度依赖关系.结合电导率的测试结果和 W-F定律可知,当温度低于450K时,声子热导率起主导作用,电子热导率几乎为0;在温度高于450K时,由于薄膜从非晶态转化为晶态,电子热导率和声子热导率同时增加.晶态薄膜的热导率随温度变化不明显,则是因为电子热导率和声子热导率分别与温度呈正负相关的关系,是二者共同作用的结果.

