多层克隆选择的排序学习方法研究

武宇婷，张子旸，田玉玲，张弘弦

(1.太原理工大学 信息与计算机学院，太原 030024；2.上海交通大学 电子信息与电气工程学院，上海 200030)

排序学习是信息检索领域最受关注的技术之一，并且广泛应用于文档分类、文本处理、产品分级及其他涉及排序问题的领域。排序学习提供了一种优秀的自动化框架进行特征组合，这些组合可以查询依赖特征，如通过现存搜索引擎给文档赋予分数，也可以是查询独立特征，如pagerank信息。

排序学习作为一种机器学习技术，从训练集的角度可以分为监督式学习和半监督式学习。监督式学习中，排序学习算法都使用一组带有标签的查询文档对作为训练数据去训练排序模型[1]；而在非监督式学习中，排序学习算法使用一小部分有标签的查询文档对将多数无标签的查询文档作为训练集[2]。训练数据中，文档与查询是否相关取决于相关性标签，通常这些标签都是人工进行判断。从学习过程的角度，排序学习可以分为批处理学习和在线学习。经典的排序学习算法大多属于批处理学习，学习过程中将一次性使用全部的训练数据，通常使用的数据集是微软发布的LETOR数据集[3]。批处理排序学习只需要一个训练过程，一旦模型训练完成就可以应用于新的查询和新的语料库，根据特征计算相关性并学习最终模型的过程只需要进行一次。在线排序学习将排序学习问题建模，用户和搜索引擎之间持续循环交互，搜索引擎随时提供给用户最好的搜索结果，搜索引擎可以与交互的用户学习并改善排序模型[4]。在经典排序学习的基础上，文献[5]提出一种在线排序学习框架，在线排序学习允许检索系统直接与用户点击反馈来优化自身性能。

排序学习技术可以根据不同的应用场景，结合不同领域的特征知识来产生面向特定问题的排序模型，如文献[6]使用排序学习解决专家检索问题，并在计算机科学的学术出版物数据集上进行试验。文献[7]使用排序学习技术构建了一个热门手机游戏预测系统，并发现了MART算法在训练模型及预测样本时具有最好的精度。文献[8]阐述了排序学习在软件工程领域任务中所带来的价值。奚凌然等人提出一种结合LPA半监督学习的排序方法，基于已标注训练数据使用Pairwise模型的Ranking SVM 进行排序学习[9]。文献[10]提出了一种基于深度学习的新的两两排序算法，并将其应用于图像重新排序。

排序学习算法的关键是选择待优化的损失函数。在IR(信息检索，Information Retrieval)中，排序结果是使用IR评价指标进行评价的，因此评价指标函数是用于优化的损失函数。但是，评价指标函数不能达到传统机器学习技术对损失函数的要求，大多数优化算法要求损失函数是平滑函数或者是凸函数，而IR评价指标函数是基于位置不连续也不可微的，现有的算法很多是通过最小化IR评价指标函数的上界函数解决平滑问题[11]，这些方法包括RankBoost，RankSVM，ListNet，AdaRank等算法。这些算法依赖于损失函数的数学解析性质，其明显的缺陷在于损失函数是IR指标的上界函数，并不能保证上界函数的最优解就是IR评价指标函数的最优解。针对这个问题，已有学者提出了基于生物理论的排序学习方法，其显著特征是直接对IR评价指标函数进行优化而无需选择替代函数，使训练结果比传统方法更精确，例如，基于遗传算法的排序学习方法及其改进算法[12]，基于免疫规划的排序学习方法[13]。

本文将IR评价指标函数直接作为亲和力函数，根据克隆选择理论产生亲和力最高的抗体(排序函数)，避免了使用损失函数的方法所带来的缺陷；将改进的克隆选择算法应用于排序学习，提出了一个直接优化IR指标函数的排序学习算法——基于多层克隆选择的排序学习算法(RankMCSA)。算法使用多层进化的方法逐步得到最优的排序函数，同时使用满二叉树的方法表示抗体，将一个查询及其相关文档集和对应的相关性判定作为抗原，定义了对二叉树按层变异的规则。算法直接使用IR指标MAP(mean average precision)作为进化过程中的亲和力函数。

1 排序学习

信息检索中的一个核心问题就是决定文档与用户的信息需求是否相关并进行排序，排序的目的是根据每个文档与用户查询之间的相关度定义文档的顺序，最后把相关文档排在检索列表的较高位置。在测试阶段，给定一个查询，系统返回一个文档的排序列表，它是按照相关性分值降序排列，而相关性分值是使用排序函数进行计算的。在训练阶段，给出一组查询和每个查询各自对应的相关文档列表，以及以全序的方式表达文档排列的相关性判定。学习的目的是构建一个排序函数，基于学习的排序方法能够组合更多的特征，具有更强的适应性。图1给出了基于学习的方法处理IR排序问题的一般框架。

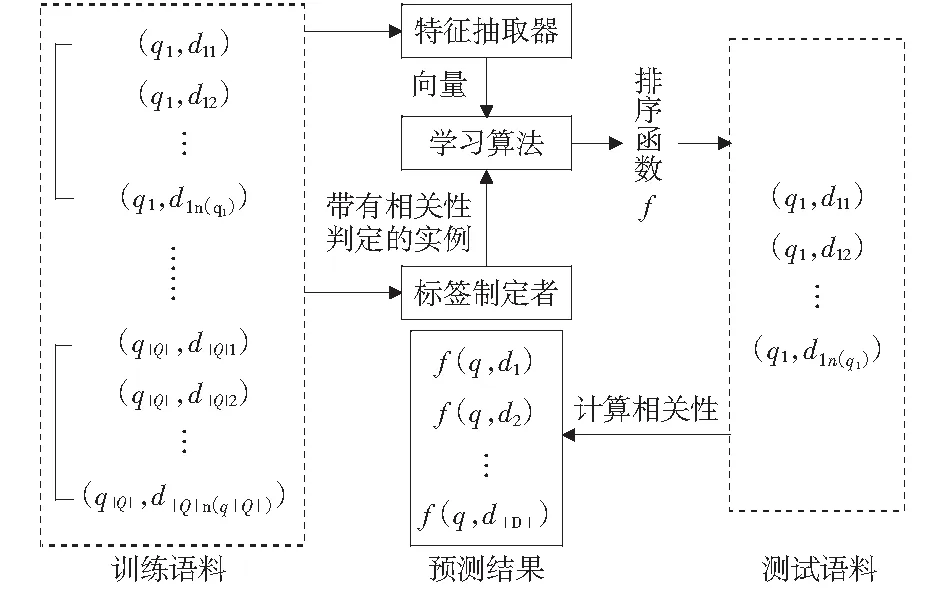
图1 信息检索领域排序学习一般框架Fig.1 A general framework of rank method with information retrieval

给定一个查询集合Q={q1,…,q|Q|}，其中每一个查询qi都有一个相关的文档列表为di={di1,di2,…,di,n(qi)}，n(qi)是文档列表的大小。创建的训练数据集由查询及其相关文档对(qi,dij)组成，文档对的相关性判定表明了qi和dij之间的关系，相关性判定由标签制定者分配，qi相关文档的标签列表为yi={yi1,yi2,…,yi,n(qi)}.相关性判定可以是以下几种情况：

a.一个类标签，如相关和不相关；

b.一个等级，如绝对相关，可能相关，不相关；

c.一个顺序，如k，意味着dij排在第k位置；

d.一个分数，如sim(qi,dij)，表示qi和dij之间的相关性分数。

对每一个查询文档对(qi,dij)，一个特征抽取器φ都会产生一个特征向量x=φ(qi,dij)描述qi和dij之间的匹配。特征包含了经典IR特征(如tf，idf，BM25)，以及其他高级特征(如 PageRank)。学习算法的输入包含训练实例、特征向量和对应相关性判定，表示为(qi,di,yi)，整个训练集可表示为

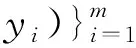
(1)

式中：m是查询的数量。训练的输出是一个排序函数f，f(qi,dij)期望能够给出qi和dij“真”的相关性判定，f作用在文档列表di上就得到预测的文档顺序πi=f(qi,di).在训练阶段，学习算法生成一个排序函数，学习过程旨在将假设空间中的排序函数所输出的相关性判定的有关指标(如分类精度，错误率，MAP等)进行优化。在测试阶段，对于qi，排序函数得到的πi关于yi的评价函数为E(πi,yi).评价函数通常包括MAP，NDCG@n(Normalized Discounted Cumulative Gain)，P@n.

2 多层克隆选择的排序学习方法

2.1 排序学习框架

在多层克隆选择的排序学习中，初始抗体库P0作为框架的第0层，使用训练集进行进化过程的学习；进化完成后，从抗体库中按照一定比例选择一组最佳抗体构成新的抗体库；抗体的选择按照抗体在训练集和验证集上的平均表现而定，其选择的比例由选择因子SELECTFACTOR∈(0,1)决定；选择的抗体数量不为1则进入到下一层继续进化，直到得到的抗体库中只有1个抗体，则停止进化，并将该抗体作为最优排序函数。多层克隆选择的排序学习框架如图2所示。

图2 RankMCSA框架Fig.2 The frame of RankMCSA

2.2 排序学习过程

在排序学习框架的每一层中最关键的两个操作是进化过程和选择过程。进化过程利用了克隆选择算法，克隆选择算法具有学习、搜索、进化等能力，可以在假设空间中找到一批较优解。克隆选择算法中，抗体库中的抗体朝着抗原识别率高的方向进化，通过计算抗原-抗体亲和力来进行选择、克隆、成熟、再选择等操作，最终获得一个高亲和力的抗体库。为了进一步筛选出更高亲和力抗体，再计算每个抗体在训练集和验证集上的平均亲和力，优先选择平均亲和力大的抗体进入下一层进行进一步进化，直到筛选出一个最佳抗体。

3 克隆选择架构

3.1 进化过程

进化过程借鉴了克隆选择算法，并对其进行改进，改进后的进化过程能够在训练集上进行学习，最终可以得到一批较优的排序函数。进化过程主要存在两个方面的改进：

1) 记忆高亲和力抗体的方式。进化过程将选择出的高亲和力抗体与成熟抗体集进行合并，并去除冗余，以保证优秀抗体被保留下来。用于排序学习的训练数据集是静态集合，作为抗原集，具有相对稳定性。

2) 添加录取因子。传统方法不能控制成熟抗体集中优秀抗体的录取比率，如果单纯通过克隆因子的增长降低录取率则不能保证抗体多样性，且不能精确控制录取率。理论上录取率越高，说明被录取抗体多样性越差，抗体质量越低。改进算法的克隆选择过程中，通过判断录取率是否高于期望值来精确控制录取率，保证在期望的低录取率下选择抗体，以提高抗体质量，如果录取率高，则随机产生一定数量的抗体加入到待选抗体集。进化过程如图3所示。

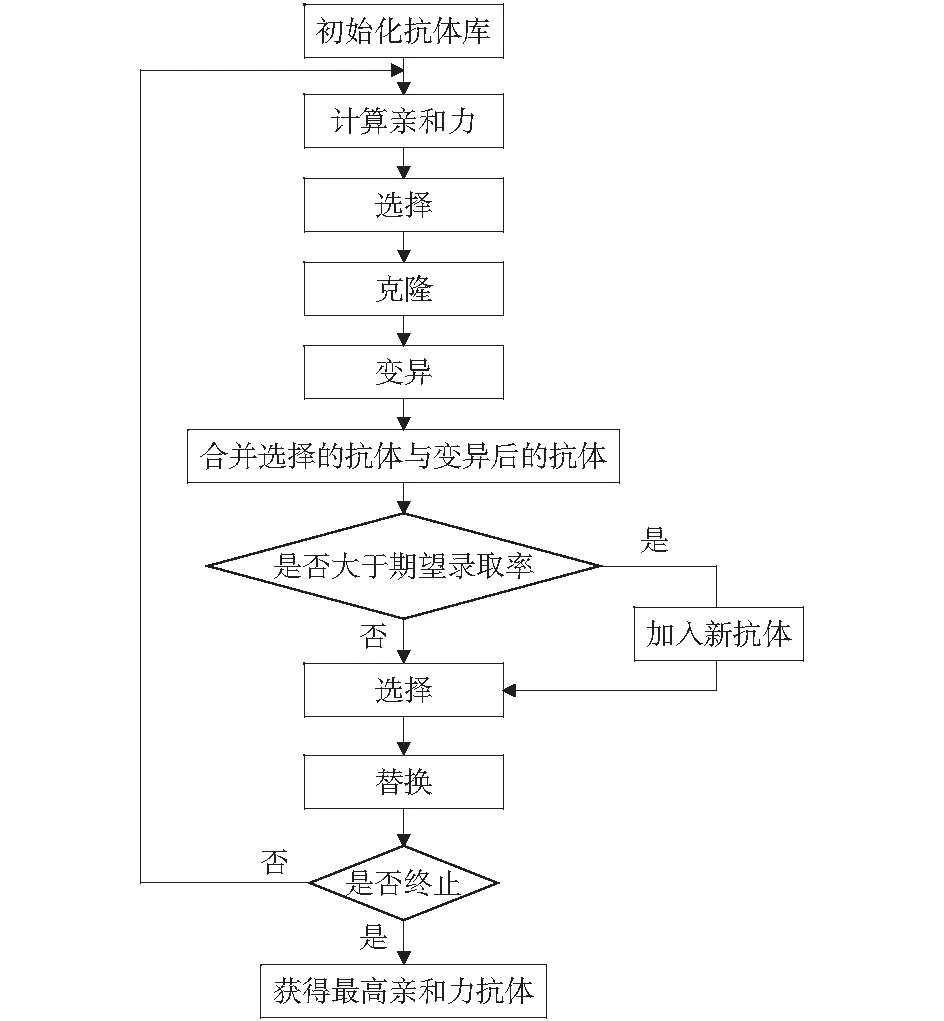
图3 每一层中抗体库的进化流程图Fig.3 The evolutionary flow chart of antibody library with each layer

3.2 抗体、抗原和亲和力

在排序学习中，抗体表示排序函数，即计算查询文档对相关度的函数，表示为bi=f(x).由抗体组成的集合称为抗体库P，将其定义为

(2)

将查询文档对表示为一个多维实数特征向量，这个向量通常是通过特定的特征提取获得。实数向量在函数中充当变量的角色，抗体可以根据不同的实数向量计算相应查询文档对的相关性分值，函数中除了包含变量之外，通常还需要运算符和常数。如f(x)=(2×x1+3×x2)/(4-x3)；其中，特征向量x=(x1,x2,x3)是一个3维的实数向量，运算符是集合{+,×,/-}中的元素，常数为2，3，4.

根据以上分析，可知抗体由3种不同元素组合而成，组成抗体的元素称为基因，则抗体的基因库定义如下：

基因库I为一个三元组I={F,O,C}，F为特征集、O为运算符集、C为常数集。

本文中定义基因库如下：

F={fi|fi∈x,i∈Z∧i∈[1,dimension(x)]}，dimension(x)是向量x的维数。

O={+,-,×,/} ,

C=

{0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1.0,

2.0,3.0,4.0,5.0,6.0,7.0,8.0,9.0,10.0} .

在排序学习中，抗原定义为以查询为单位的文档列表和标签列表

gi=(qi,di,yi) .

(3)

由抗原组成的抗原集定义抗原库R

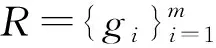
(4)

亲和力函数计算抗体与抗原的相关度，在排序学习中亲和力函数定义为IR评价指标函数

affinity(bi,gj)=E(πi,yi) .

(5)

衡量某个抗体bi的好坏不能仅仅以个别抗原的亲和力为标准，而是要以抗原库的所有抗原的亲和力的平均值为标准。所以，评价指标计算方法E(πj,yj)一般设置为MAP，因为该指标衡量排序函数在整个测试集上的平均表现。抗体bi在抗原库R上的平均亲和力定义如下:

(6)

抗体的数据结构使用满二叉树结构，树表示法由于更加容易理解与计算，抗体树内部节点表示运算符，叶子节点表示特征和常数。一个抗体表示一个候选的排序函数，中序遍历满树后，得到候选函数的表达式。叶子节点中的特征随机从F和C中获取，抗体的最后表达式不要求覆盖所有的特征，并且同一个特征可以在一个树的叶子中出现多次。通过使用满二叉树表达抗体，如图4所示的树通过中序遍历即可生成函数(3-f1)+(f2×0.3).

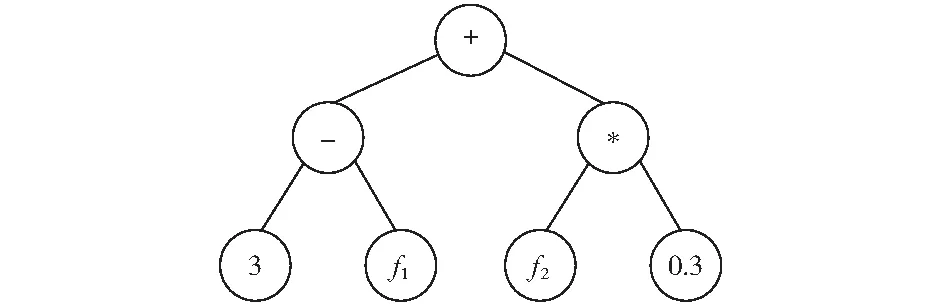
图4 抗体树表示Fig.4 The representation with antibody tree

3.3 选择过程

在抗体库P0进化结束后，需要选择优秀的抗体进入下一层P1继续进化。选择的抗体数量由选择因子fSEL确定，第i层抗体库Pi的抗体数量定义如下:

|Pi|=round(fSEL·|Pi-1|) .

(7)

式中：i≥1，fSEL∈(0,1).

为了选择最佳抗体，计算抗体Abi在训练集D和验证集V上的平均亲和力

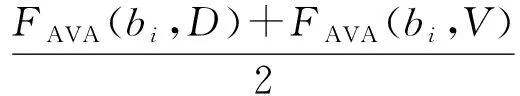
(8)

式中，FAVA(bi,D)表示抗体bi在训练集D上的亲和力。将抗体库Pi-1中所有抗体按照公式(8)计算后，根据公式(7)选择亲和力最高的抗体进入下一层继续进化。当抗体库中抗体数量为1时，整个训练过程结束并将该抗体作为最优的排序函数。

3.4 算法描述

基于多层克隆选择的排序学习利用一个多层的克隆选择过程学习最优的排序函数。学习过程主要包括以下几个步骤：

1) 随机生成一个原始排序函数集作为第0层的抗体库，初始化由查询文档对构成的训练集D、验证集V；

2) 遍历每一个排序函数，计算其在训练集上的MAP；

3) 根据MAP的大小对排序函数进行选择、克隆、变异，并迭代操作这些过程直到满足迭代终止条件，进化完成后根据选择因子fSEL选择一定数量优秀的排序函数进入下一层；

4) 持续对排序函数集合进行进化，直到获得一个最优排序函数。

多层克隆选择的排序学习算法描述如下：

输入：训练集D，验证集V.

参数：N(抗体库大小)，n(待克隆抗体数量)，T(迭代次数)，d(替换抗体数量)，α(录取因子)，β(克隆因子)，fSEL(选择因子)。

Step2：计算每个排序函数bi∈P在D上的MAP；

Step3：根据MAP的值，从P中选择n个最高MAP的排序函数组成Pn；

Step4：对Pn中的排序函数进行克隆得到克隆集C，MAP越高克隆副本越多，C的大小为Nc；

Step5：对C中的排序函数进行变异得到成熟集C*，MAP越高，变异层数越少，C*的大小为Nc；

Step6：将Pn与C*合并，去除相同排序函数，得到P*；

Step7：IfN/P*>αthen随机生成(N/α-|P*|)个排序函数加入到P*；

Step8：从P*中选择MAP最高N个排序函数组成P*；

Step10：重复Step1到Step9，直到满足迭代次数大于T；

Step11：从P中选择若干最好排序函数，进入到下一层。如果P中只剩下一个排序函数，则算法停止并返回这个最优的排序函数。

3.5 克隆与变异

抗体库中的每个抗体克隆的数量与平均亲和力成正比。每个抗体的克隆数量表示为

NCLO=round(β×n×FAVA) .

(9)

式中：β是克隆因子；n是选择抗体的数量；FAVA是抗体的平均亲和力；round函数对小数点后1位四舍五入，最后得到一个整数。克隆后的所有克隆抗体的数量为

(10)

抗体变异方法使用的是子树替换方式，根据亲和力选择抗体的一个内部节点，然后通过随机生成一个树去替换该节点为根的整个子树。变异操作需要满足以下规则：

1) 替换后的节点编号要符合整个树的编号顺序。

2) 替换子树的特征与被替换子树的特征完全相同且不重复，新子树特征节点排列是随机的。这样做是为了变异后的抗体同样能够完全覆盖所有特征且不重复。

分层变异策略定义如下：

根据亲和力计算变异发生的层数l.

l∈[0,H-1]∧l∈Z.H为树的高度，第0层为抗体的根节点。

1) 随机选择该层的一个内部节点n，获取以该节点为根的子树高度h.

2) 获取该节点为根的特征子节点数组f[].为了保留原有特征节点编号，将其随机挂载进新的子树上，这样整个抗体的特征仍然不重复且完全覆盖所有特征。

3) 创建高度为(h-1)的子树t.

4) 创建包含f[]所有元素的叶子节点l[]，数量为2(h-1).

5) 随机选取l[]中的叶子，挂载到t上面，构成一个高度为h的子树。

6) 用子树t替换子树n.

在变异时，抗体根据抗体亲和力选择变异层，亲和力越大所选变异层越大，替换子树越小。

假设亲和力FAVA∈[Fmin,Fmax]，树的高度为H，要使得l∈[0,H-1]∧l∈Z，则变异层的计算方法如下

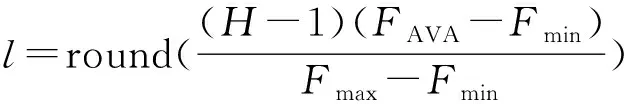
(11)

对于不在亲和力区间内的亲和力值，采用下面策略：

IfFAVA∈(0,Fmin) thenl=0 ,

IfFAVA∈(Fmax,1) thenl=H-1 .

亲和力区间根据经验确定，所选区间和实际相关度的变化区间越相符，则所选的层次数越有效。亲和力区间与数据集有关，不同的数据集亲和力差别较大，具体的区间范围要根据实际情况而定。

4 排序学习实验

实验使用数据集LETOR3.0中的OHSUMED数据集以及LETOR4.0中的MQ2007，MQ2008数据集。LETOR数据集包含了IR相关的特征，查询文档对的相关性判断和用于交叉验证的数据分区，并且还提供了标准的评价工具以及用于比较的基线结果。LETOR数据集全部采用5-fold交叉验证的方式，算法的运行结果是5-fold的平均结果。

评价指标使用了MAP(mean average precision)，NDCG(normalized discounted cumulative gain)和P@n.实验所用的评价工具是LETOR提供的标准评价工具，保证和基线比较的正确性。MAP的计算方法如公式(12)和(13)

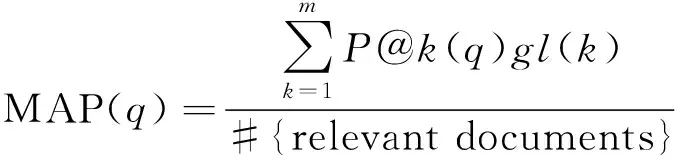
(12)

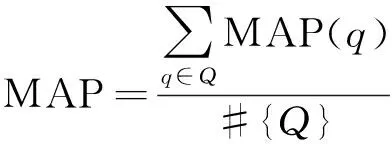
(13)

式中：P@k(q)为位置k的准确率；位置k的文档标签为l(k)；l(k)等于1表示文档相关，等于0表示文档不相关；m是该查询相关的文档数量。MAP只支持二值相关性判断。另一个指标为NDCG支持多个相关度判断，对某个位置j来说，查询集上所有查询的平均值NDCG(j)越大，表示相关性越大的文档排序越靠前，计算方法如式(14)：

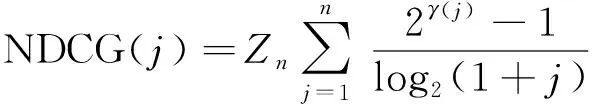
(14)

4.1 实验设置

利用所提出的算法对每个fold的训练集进行训练，训练结束后得到一个最优的排序函数。使用该函数计算测试集中的每个查询文档对的相关性分值，得到一个包含相关性分值的预测文件。使用LETOR提供的标准测试工具对预测文件进行处理得到最后的MAP和NDCG评价结果。每次实验的5-fold的平均结果是算法在该数据集上的运行结果。实验中，所提出的RankMCSA算法分别在OHSUMED和MQ2008数据集上执行10次，每次执行都是5-fold交叉验证，最后的实验结果是10次实验的平均值。所提出的算法在2个数据集实验参数设置如表1所示。

4.2 实验结果

本文将RankMCSA与下面4种基线方法进行比较：RankSVM,RankBoost,ListNet和AdaRank-MAP.表2显示了2个数据集的MAP值的比较。图5显示了OHSUMED数据集上RankMCSA算法的NDCG@n值的比较，图6显示OHSUMED数据集上RankMCSA算法的P@n值的比较，图7是MQ2008数据集上RankMCSA算法的NDCG@n值的比较，图8是MQ2008数据集上RankMCSA算法的P@n值的比较。

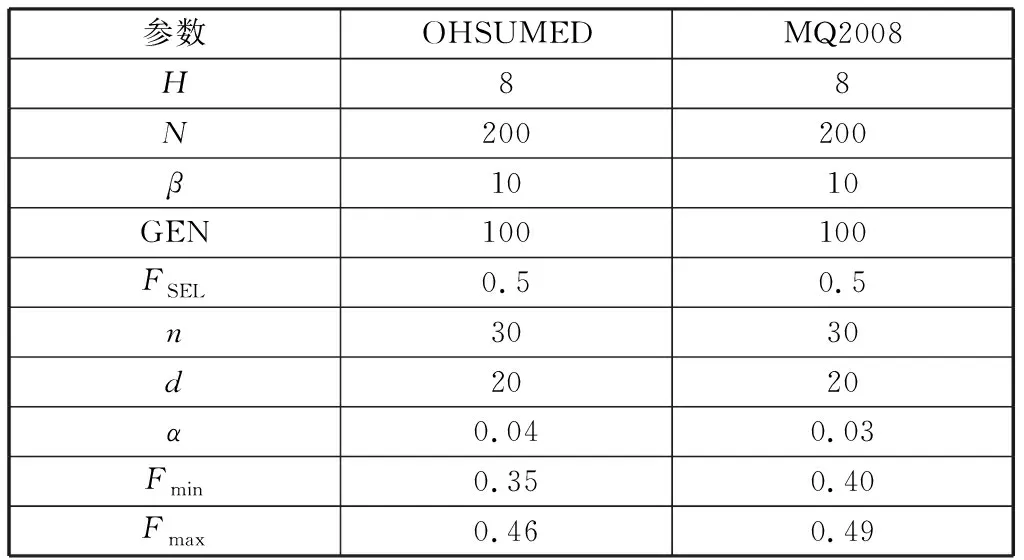
表1 实验参数Table 1 Experiment parameter

表2 RankMCSA算法的MAP值比较Table 2 The comparison of MAP's values above the algorithm of RankMCSA

图5 OHSUMED数据集上RankMCSA的NDCG@n值的比较Fig.5 The comparison of NDCG@n's values of RankMCSA above the data sets of OHSUMED

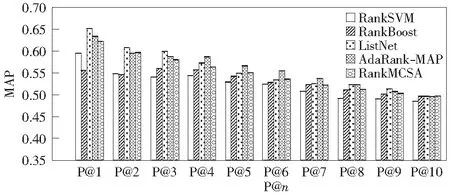
图6 OHSUMED数据集上RankMCSA的P@n值的比较Fig.6 The comparison of P@n's values of RankMCSA above the data sets of OHSUMED

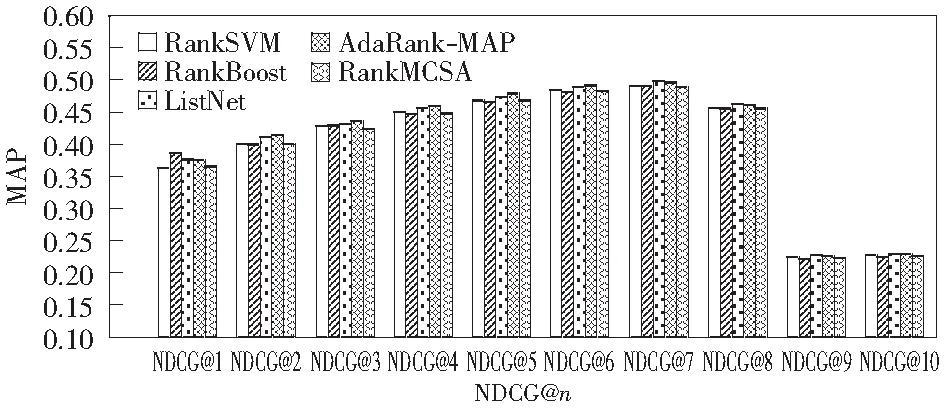
图7 MQ2008数据集上RankMCSA的NDCG@n值的比较Fig.7 The comparison of NDCG@n's values of RankMCSA above the data sets of MQ2008

图8 MQ2008数据集上RankMCSA的P@n值的比较Fig.8 The comparison of P@n's values of RankMCSA above the data sets of MQ2008

表2中，RankMCSA在OHSUMED上的MAP比RankSVM高出2.1%，比RankBoost高出0.3%；但是比ListNet和AdaRank-MAP分别低0.69%和1.3%.在MQ2008上RankMCSA比RankSVM高出1.7%，比AdaRank-MAP高出0.2%，比RankBoost和ListNet低0.02%，几乎相同。对于NDCG@n指标，从图5可以看出OHUSMED上RankMCSA明显好于RankSVM和RankBoot，但稍逊于ListNet和AdaRank-MAP.而从图7可以看出MQ2008上RankMCSA与基线算法的差别并不明显，平均表现与基线持平。对于P@n指标，从图6可以看出OHSUMED上RankMCSA明显优于RankBoost和RankSVM，但对比ListNet和AdaRank-MAP仍显不足。从图8可以看出RankMCSA仍然表现稳定，平均表现与基线算法持平。从图5-图8中可以看出，RankMCSA比基线算法更稳定，波动较小，这说明该算法不仅能将相关度高的文档排在前面，而且对高排名位置敏感程度低，从而避免出现高排名的文档相关度高低差别大的情况。

从以上结果中可以看出，RankMCSA是一种能够产生有效排序函数的排序学习算法，在2个数据集上明显优于RankSVM，RankBoost.在OHSUMED集合上，在某些情况下优于ListNet，如NDCG@4～NDCG@7，P@5,P@6，与AdaRank-MAP相比略显不足。在MQ2008上，各个算法的差别并不明显，这也证明了RankMCSA算法的有效性。算法仍然有可以提升的空间，随着抗体库大小、克隆因子以及选择因子的提高，算法的运行结果会进一步得到改进。

5 结束语

本文提出了一种基于多层克隆选择的排序学习方法，用于学习IR中的排序函数。它使用一种按层变异的方法和一种多层的克隆选择架构逐步进化抗体库，每一层进化完成后选择一定数量的优秀抗体进入下一层，直到最后遴选出最优排序函数；这种方法对于生成复杂的、非线性排序函数非常有效。同时使用满二叉树的方法表示抗体，将一个查询及其相关文档集和对应的相关性判定作为抗原，定义了对二叉树按层变异的规则。算法在OHSUMED和 MQ2008数据集上进行实验，结果表明RankMCSA能够在更少的迭代次数以及更少的训练时间内产生更好的排序函数；不仅能将相关度高的文档排在前面，而且对高排名位置敏感程度低，从而避免出现高排名的文档相关度高低差别大的情况。