Physicochemical Properties of1-Methoxyethyl-3-Methylimidazolium Glycine

WEI Jie, DONG Hexin, CHEN Xia, YANG Yuxuan, FANG Dawei , GUAN Wei , YANG Jiazhen

Institute of Rare and Scattered Elements, College of Chemistry, Liaoning University, Shenyang 110036, P. R. China.

Abstract: Because of the unique acid-base behavior of amino acids,we combined glycine as the anion with an ether group as the cation and prepared a novel ionic liquid (IL), 1-methoxyethyl-3-methylimidazolium glycine [MOEMIM][Gly]. The formation of this IL was confirmed by 1H-NMR, 13C-NMR, differential scanning calorimetry (DSC) and thermogravimetry (TG) analyses. The density, ρ, and surface tension, γ,of the ILs were measured in the temperature range from 298.15 K to 338.15 K at intervals of 5 K using the standard addition method,because the strong hydrogen bonds between the IL [MOEMIM][Gly]and trace amounts of water made it, extremely difficult to remove water by convention methods. The calculated molar volume, Vm, of [MOEMIM][Gly] increased with increasing temperature. The thermal expansion coeff i cient, α, was also obtained based on the density values. In terms of the molar surface Gibbs free energy, gs for [MOEMIM][Gly], the traditional Eötvös equation is improved so that it has physical signif i cance, that is, the intercept C0 represents molar surface enthalpy, h, which is a temperature-independent constant and the slop C1 =−(∂gs/∂T)p is molar surface entropy, s, it shows that modified Eötvös equation is not only an empirical equation, but also a strict thermodynamic one. In addition, by a combination of gs and the modified Eötvös equation, the surface tension values of [MOEMIM][Gly] were estimated and compared with the experimental values; both sets of data were in good accordance with each other.

Key Words: 1-Methoxyethyl-3-methy limidazolium glycine; Density; Surface tension; Molar surface Gibbs free energy

1 Introduction

As a new-generation green solvent, ionic liquids (ILs) have attracted considerable attention from industry and academic community. In particular, amino acid ionic liquids are a special class of ionic liquids due to their unique acid-base behavior,biological signif i cance, and applications in different fi elds such as templates in synthetic chemistry, stabilizers for biological macromolecules1, etc. The physicochemical properties of these ionic liquids can easily be altered by making the different combinations of amino acids as anion along with possible cation modif i cation which makes the ionic liquids more suitable to understand the different kinds of molecular and ionic interactions with sufficient depth so that they can provide fruitful information for a molecular level understanding of more complicated biological processes. And in recent years,there has been a developing trend in the literature toward the ether-functionalized ILs on the carbohydrate dissolution2–5,enzymatic acylation6, extraction7,8, CO2capture9, gas separation10, and organic reactions11–14and it is also found that incorporating an ether group can have an influence on the viscosity of ILs15–18, which is drawn the attention from more and more people.

Hence, we combined glycine as anion with ether group in the cation and prepared a novel ionic liquids, and the physicochemical properties have been further investigated by the semi-empirical methods, which can not be regarded as accurate physicochemical data, although it is to be commended because it provides valuable insight into the origins of the behavior of the materials. In this paper, the new results are reported as follows: A novel ionic liquid 1-methoxyethyl-3-methy limidazolium glycine[MOEMIM][Gly] is prepared and confirmed by1H-NMR spectrum,13C-NMR spectrum, DSC and TG. The determination of densities, ρ, and surface tensions, γ, of the ILs at T =298.15–338.15 K with an interval of 5 K using standard addition method (SAM); (3) The volume properties of IL[MOEMIM][Gly] are discussed; (4) The molar surface Gibbs free energy for [MOEMIM][Gly] is calculated in different temperatures, and in terms of the molar surface Gibbs free energy, gs, the modif i ed Eӧtvӧs equation is applied to[MOEMIM][Gly]; (5) Combined the molar surface Gibbs free energy with modif i ed Eӧtvӧs equation, the surface tension is estimated.

2 Experimental

2.1 Chemicals

Deionized water with a conductance of (0.8–1.2) × 10−4S∙m−1was used in experiments. 1-Methylimidazole (AR-grade)was purchased from ACROS and vacuum-distilled prior to use.Glycine, 1-bromo-2-methoxyethane, diethyl ether, acetonitrile,methanol and anion-exchange resin (type 717) were purchased from Shanghai Chemical Reagent Co. Ltd. and glycine was recrystallized twice and was dried under reduced pressure,anion-exchange resin (type 717) was activated by the regular method before use. The purity and some related information of the chemicals are listed in Table S1.

2.2 Preparation of [MOEMIM][Gly]

[MOEMIM][Gly] were prepared by the neutralization method as described in the literatures19,20. Under the protection of argon, a solution of 1-methylimidazole (1 eq) and 1-bromo-2-methoxyethane (1.1 eq) in round-bottom flask is stirred at 25 °C for 18 h, then diethyl ether (80 mL) was added to the solution and continued to react for 36 h to obtain white solid product [MOEMIM][Br], which was washed in diethyl ether at least 3 times. Next, by use of activated anion-exchange resin, the aqueous [MOEMIM][OH] was prepared from[MOEMIM][Br]. Then aqueous [MOEMIM][OH] was added dropwise to a slightly excess glycine aqueous solution, and then it was stirred for 50 h. The scheme shows the synthetic route (see Scheme 1). Then water was evaporated under reduced pressure. To this reaction mixture was added the mixed solvent acetonitrile/methanol (volumetric ratio = 9/1), and it was stirred befittingly. The mixture was then fi ltered to remove excess glycine. Filtrate was evaporated under reduced pressure to remove solvents. The product of [MOEMIM][Gly] was dried in vacuo for 2 days at 80 °C. Structures of the resulting[MOEMIM][Gly] were conf i rmed by1H-NMR spectrum,13C-NMR spectrum, DSC and TG (see Figs. S1–S4 in Supporting Information).

Scheme 1 Synthesis of functionalized IL [MOEMIM][Gly].

Element analysis show the purity of the synthesized ionic liquids is more than 0.99.

Mass fraction of water in [MOEMIM][Gly] determined by a Karl Fischer moisture titrator (ZSD-2 type) is 380 × 10−6. Ion selective electrode measurements reveal that the mass fraction of halogen (Br−) is less than 210 × 10−6.

2.3 Determination of density and surface tension for[MOEMIM][Gly]

It is extremely difficult to remove any water in[MOEMIM][Gly] by conventional methods because the ionic liquid can strongly form hydrogen bonds with water, so the SAM21–23is applied in these measurements in order to eliminate the effect of water. According to SAM, a series of samples of [MOEMIM][Gly] with various mass fraction of water were prepared.

An Anton Paar DMA 4500 oscillating U-tube densitometer is used to measure the density of a series of samples. The temperature in the cell is regulated to ±0.03 K with solid state thermostat. Before measurement, the apparatus was calibrated once a day with dry air and double-distilled freshly degassed water. Using the calibrated densitometer, the densities of the degassing water are measured at T = 298.15–338.15 K with interval 5 K and was in good agreement with the literature24within experimental error. Then the densities of all samples are measured by the densitometer in the same temperature range.

Using the tensiometer of the forced bubble method (DPAW type produced by Sang Li Electronic Co.), the surface tension of water is measured at T = 298.15–338.15 K and was in good agreement with the literature24within experimental error. Then the values of surface tension of the samples are measured by using the same method in the same temperature range.

3 Results and discussion

3.1 The values of density, ρ, and surface tension, γ,of IL [MOEMIM][Gly]

The values of density and surface tension for the samples of[MOEMIM][Gly] containing various contents of water are listed in Tables 1 and 2, respectively. Each value in the tables is the average of triplicate measurements. According to the SAM,the values of density and surface tension of the samples are plotted against the mass fraction of water, w2(w2is the mass percentage) respectively, so that a series of good straight lines are obtained (see Figs. 1 and 2). The values of correlation coeff i cient, r, for all linear regressions are larger than 0.998 and all values of standard deviation, SD, are within standarduncertainty of the measurement. The intercepts of the straight lines are the values of density or surface tension of[MOEMIM][Gly] without water and can be viewed as experimental values, which are listed in the 7th column of Tables 1 and 2, respectively. From these data, it turned out that using the SAM is appropriate. Standard uncertainties (0.68 level of conf i dence) for temperature, pressure and water mass fraction are listed in the footnote of Tables 1 and 2, and the expanded uncertainties Uc(0.95 level of conf i dence) for density and surface tension are also listed in the 7th column of Tables 1 and 2, respectively.

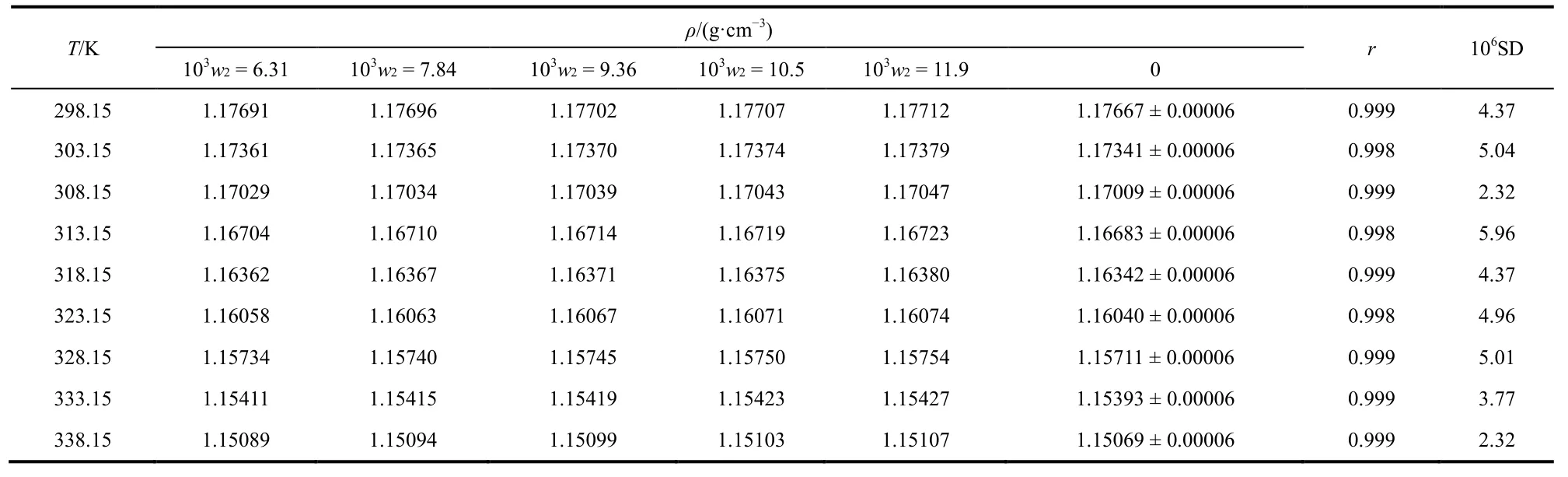
Table 1 At T = (298.15–338.15) K a and pressure p = 0.1 MPa b, density values for [MOEMIM][Gly], ρ, mass fraction of water, w2 c in[MOEMIM][Gly].

Table 2 At a T = (298.15–338.15) K and pressure b p = 0.1 MPa, surface tension values for [MOEMIM][Gly], γ,mass fraction of water, c w2 in [MOEMIM][Gly].

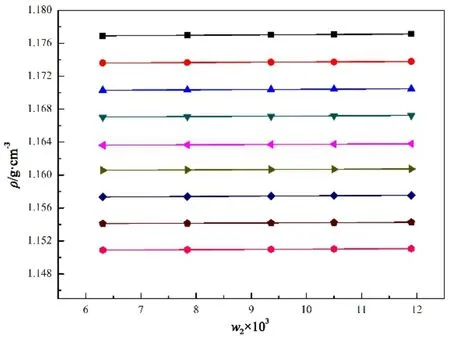
Fig. 1 Plot density, ρ, vs mass fraction of water, w2 in[MOEMIM][Gly] in the temperature range of 298.15–338.15 K.298.15 K: ρ = 1.17667 + 3.8225 × 10−5w2, SD = 4.37 × 10−6, r = 0.999.303.15 K: ρ = 1.17341 + 3.2434 × 10−5w2, SD = 5.04 × 10−6, r = 0.998.308.15 K: ρ = 1.17009 + 3.2414 × 10−5w2, SD = 2.32 × 10−6, r = 0.999.313.15 K: ρ = 1.16683 + 3.3917 × 10−5w2, SD = 5.96 × 10−6, r = 0.998.318.15 K: ρ = 1.16342 + 3.1735 × 10−5w2, SD = 4.37 × 10−6, r = 0.999.323.15 K: ρ = 1.16040 + 2.8905 × 10−5w2, SD = 4.96 × 10−6, r = 0.998.328.15 K: ρ = 1.15711 + 3.6111 × 10−5w2, SD = 5.01 × 10−6, r = 0.999.333.15 K: ρ = 1.15393 + 2.8825 × 10−5w2, SD = 3.77 × 10−6, r = 0.999.338.15 K: ρ = 1.15069 + 3.2514 × 10−5w2, SD = 2.32 × 10−6, r = 0.999.

3.2 Volumetric properties of [MOEMIM][Gly]

According to the definition of molar volume, Vm:

where M is molar mass, ρ is the density. From experimental values of density, the molar volume, Vmof [MOEMIM][Gly] at T = (298.15–338.15) K are calculated and the results are listed in Table 3. These results indicate that the values of Vmincrease with the increasing of temperature.

In addition, according to def i nition of thermal expansion coeff i cient, α:

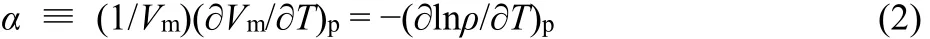
where Vmis molar volume. Plotting lnρ vs T, the straight line was obtained (see Fig. 3), and the slope is the thermal expansion coeff i cient, that is α = 5.58 × 10−4K−1for[MOEMIM][Gly], which can be seen as experimental value of thermal expansion coeff i cient.

3.3 The mole surface Gibbs free energy and the modif i ed Eötvös equation

Fig. 2 Plot surface tension, γ, vs mass fraction of water, w2 in[MOEMIM][Gly] in the temperature range 298.15–338.15 K.298.15 K: γ = 47.5 + 0.4906w2, SD = 5.45 × 10−2, r = 0.999.303.15 K: γ = 47.2 + 0.4707w2, SD = 2.31 × 10−2, r = 0.999.308.15 K: γ = 46.9 + 0.4572w2, SD = 4.29 × 10−2 , r = 0.999.313.15 K: γ = 46.5 + 0.4572w2, SD = 4.29 × 10−2, r = 0.999.318.15 K: γ = 46.1 + 0.4504w2, SD = 3.89 × 10−2, r = 0.999.323.15 K: γ = 45.8 + 0.4369w2, SD = 3.78 × 10−2, r = 0.999.328.15 K: γ = 45.1 + 0.4569w2, SD = 5.58 × 10−2, r = 0.999.333.15 K: γ = 44.5 + 0.4706w2, SD = 2.31 × 10−2, r = 0.999.338.15 K: γ = 44.1 + 0.4706w2, SD = 2.31 × 10−2, r = 0.999.

For most of the liquids, the relationship between surface tension and the temperature is usually expressed as Eötvös equation25:

where γ is surface tension, Vmis molar volume, Tcis critical temperature and kE, which is related to polarity of the liquid, is Eӧtvӧs constant. Although the traditional Eӧtvӧs empirical equation can well explain the relationship between surface tension and temperature, in which the physical signif i cance of γVm2/3is not clear and the dimension (J·mol−2/3) is not convenient to use. So we used a new thermodynamic function,the molar surface Gibbs free energy, gs, derived by Tong et al.26,27and Guan et al.28and it has been applied to the properties of ionic liquids for the first time.

The def i nition of gsis:

where γ is surface tension, Vmis molar volume and N is Avogadro constant. The values of gscalculated from Eq. (4) are listed in the fourth column of Table 3. Plotting gsversus T, a straight line is obtained (see Fig. 4), the correlation coeff i cient of the linear regression is 0.99.

The relationship between the molar surface Gibbs free energy, gs, and temperature, T can be expressed in the following improved empirical equation:

where C0and C1are empirical parameters, C1= 19.17 J∙K−1∙mol−1, C0= 18.70 kJ∙mol−1with relative coeff i cient r =0.99 and sd = 0.0012 for [MOEMIM][Gly]. That is to say,based on the molar surface Gibbs free energy, gs, the Eӧtvӧs empirical equation is improved.

3.4 The estimation of surface tension of[MOEMIM][Gly]

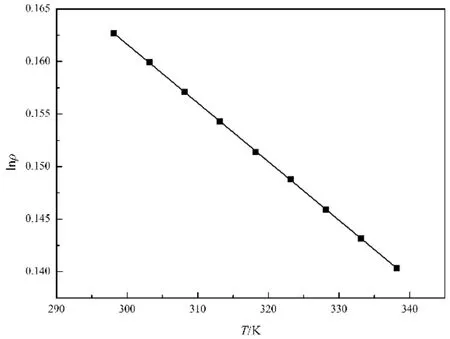
Fig. 3 Plot of lnρ vs T for [MOEMIM][Gly].lnρ = −5.58 × 10−4 T + 0.33, SD = 5.4 × 10−2, r = 0.9999.

Table 3 The values of Vm, γVm2/3, gs and γ(est) for [MOEMIM][Gly].

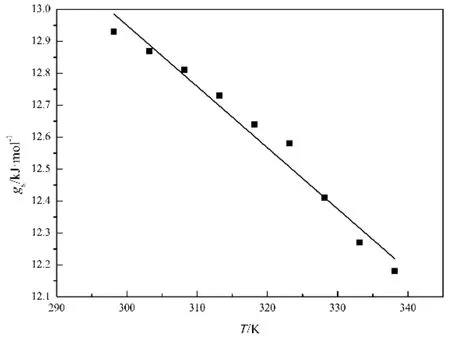
Fig. 4 Plot the molar surface Gibbs free energy, gs, vs temperature,T for [MOEMIM][Gly] in the temperature range of 298.15–338.15 K.gs = 18.70 − 0.01917T, SD = 0.0012, r = 0.99.

From the modif i ed Eӧtvӧs equation Eq. (5), it is noticed that C0and C1have clear physical signif i cance, C0represents molar surface enthalpy, h, which is a temperature-independent constant and C1= −(∂gs/∂T)pis molar surface entropy, s. Since molar surface enthalpy is independent with temperature, molar surface heat capacity cp= 0 which implies that the process from the inside to the surface of the liquid is an isocoulombic one29(an isocoulombic reaction is the one in which the number and charge of charged species are identical on both sides of the reaction. Reaction of this type tends to have near-zero heat capacity change and thus has constant enthalpy with increasing temperature). Combined Eq. (4) with Eq. (5), the values of surface tension are estimated, and are listed in Table 3. Plotting the experimental surface tension values, γ vs the estimated ones,γ(est), a good straight line was showed (see Fig. 5). The results reveal that the values of γ and γ(est) are almost consistent (the intercept = 0.2 approximately 0 and the slope = 0.995 approximately 1). These facts show that new Eötvös equation is not only an empirical equation, but also a strict thermodynamic one.

Fig. 5 Plot the experimental surface tension values, γ vs the estimated ones, γ(est) for [MOEMIM][Gly].γ = 0.995γ(est) + 0.21, SD = 0.05, r = 0.99.

4 Conclusions

A functional ionic liquids [MOEMIM][Gly] is prepared for the first time and confirmed by1H-NMR spectrum,13C-NMR spectrum and DSC. By using SAM, density and surface tension of the ILs at T = 298.15–338.15 K with an interval of 5 K have been determined, and molar volume, Vmare calculated, and these results indicate that the values of Vmincrease with the increasing of temperature. In addition, thermal expansion coeff i cient, α = 5.579 × 10−4K−1for [MOEMIM][Gly] is also obtained, which can be seen as experimental value of thermal expansion coeff i cient. Then, we used a new thermodynamic function, the molar surface Gibbs free energy, gsto improve the Eötvös equation, and the modified one has clear physical signif i cance, C0represents molar surface enthalpy, h, which is a temperature-independent constant and C1= −(∂gs/∂T)pis molar surface entropy, s. Since molar surface enthalpy is independent with temperature, molar surface heat capacity cp= 0 which implies that the process from the inside to the surface of the liquid is an isocoulombic one. In addition, the surface tension of [MOEMIM][Gly] is estimated based on the gsand the modified Eötvös equation. The results reveal that the values of γ and γ(est) are almost consistent. These turn out that improved Eötvös equation is not only an empirical one, but also a strict thermodynamic one.

Supporting Information: available free of charge via the internet at http://www.whxb.pku.edu.cn.