淮阴站降雨年内分配指标特征及相关性研究

陆小明，闫中月

（1.江苏省水文水资源勘测局，江苏 南京 210029；2.南京大学表生地球化学教育部重点实验室，江苏 南京 210023；3.南京大学地球科学与工程学院，江苏 南京 210023）

降雨是地表径流的主要来源，直接影响着径流的变化，决定着区域水资源的天然配置，同时对地区植被格局及生态环境有着深刻的影响[1-2]。因此，降雨年内分配变化规律是研究气象变化、水文循环以及环境演变的基础，一直是水文水资源学研究的主要内容，也是开展水利设计和水环境管理工作必不可少的部分。降雨年内分配特征是“降雨的时间结构”，通常用月降雨量占全年的百分比和距平百分比来表示，但其存在难以准确、全面地反映降雨年内分配的不均匀性的缺点[3]。近年来，有学者将不均匀系数[4]、信息熵[5]、集中度[6]和集中期[7]等指标单独或组合使用来开展不同地区降雨年内分配特征的研究，同时采用较常用的趋势检验方法如Mann-Kendall（M-K）检验法、距平累积法和线性回归法[8-11]开展其相应的趋势分析。然而，对于降雨年内分配各指标间相关性的研究较少。因此，本文采用常用的不均匀系数、信息熵、重心、集中度和集中期指标，开展了淮阴站降雨年内分配特征指标特征及相关性研究，以期为降雨年内分配不均匀性评价指标的选择提供参考。

1 数据与方法

1.1 数据

淮阴雨量站位于江苏省淮安市清江浦区，东经119°01′，北纬33°36′，地处淮河流域四级水文分区——渠北地区。本区域为北温带半湿润季风气候，季风特征明显，夏季炎热多雨，冬季寒冷少雨。淮阴站1951～2015年多年平均降雨量957.6 mm，年际变化大，最大年降雨量1502.3 mm（2003年），最小年降雨量492.3 mm（1966年），变差1010 mm，变化幅度较大；年内分配不均，多年平均汛期（6～9月）降雨量占全年降雨量的66.0%。

1.2 研究方法

1.2.1 年内分配分析方法

采用年内分配不均匀系数和年内分配熵、集中度、集中期及年内分配重心作为降雨年内分配的指标，从不同角度定量降雨年内分配的变化规律。年内分配不均匀系数，也称变差系数，为区域内年内月降雨量均方差与年内月平均降雨量的比值，其表征年内降雨的不均匀性。其计算公式如下：

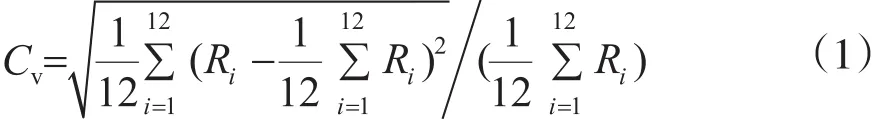
式中：Ri为年内各月降雨量。由式（1）可以看出，Cv值越大，年内各月降雨量相差越大，降雨年内分配越不均匀。分配熵可用于度量年内各月降雨量分配的不均匀性[5]，Shannon给出的熵计算公式如下：

式中：H（P）为熵函数，pi为年内各月的降雨占比。集中度和集中期是反应年内月降雨集中程度的重要指标[12-13]，其将各月的降雨量作为向量长度，1～12月的向量角度分别取0°～330°，每月间隔为30°。因此，每月的降雨量可以分解为x和y两个方向上的分量，其计算公式如下：

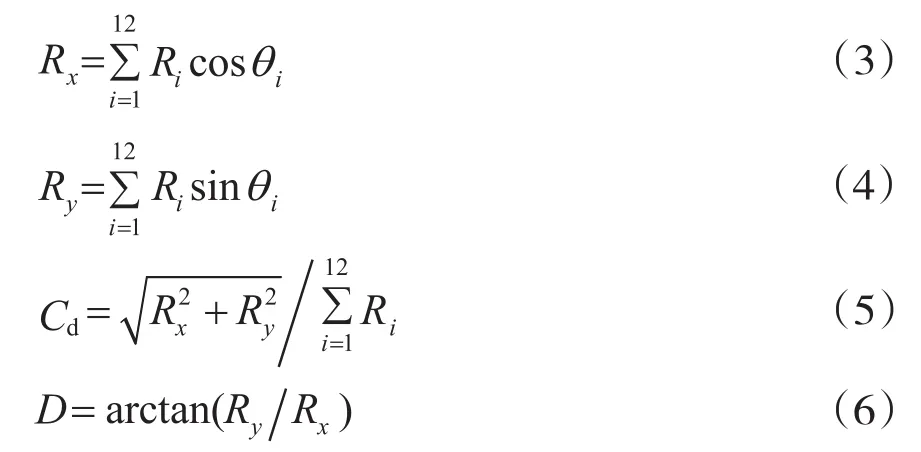
式中：Cd为集中度是经过变换后合成向量长度与年降雨量的比例，其值越大代表降雨越集中，如降雨量集中在某一月份时，其集中度为1，而降雨量均匀分布时其集中度为0。D为集中期，其是合成向量的角度，即年内降雨加权质心所在月份。重心的概念源于牛顿力学，其为物体在重力场中各部分所受重力合力的作用点。在降雨时间序列中表征降雨年内分配的集中期，其计算公式如下：

式中：G为降雨重心，i为月份，Ri为i月降雨量。

1.2.2 年际变化分析方法

Mann-Kendall检验法是一种非参数统计检验方法，其无需样本服从特定分布，也不受少数异常值的影响，在水文、气象领域通常应用于时间序列变化趋势和突变分析[10，14-18]。在趋势分析中，其通过统计量Z来判断时间序列是否存在显著趋势；在突变分析中，其通过绘制UF和UB曲线图，判断是否存在显著突变。一般显著水平取0.05，相应统计量Z、UF和UB的临界值为[-1.96，1.96][19-21]。

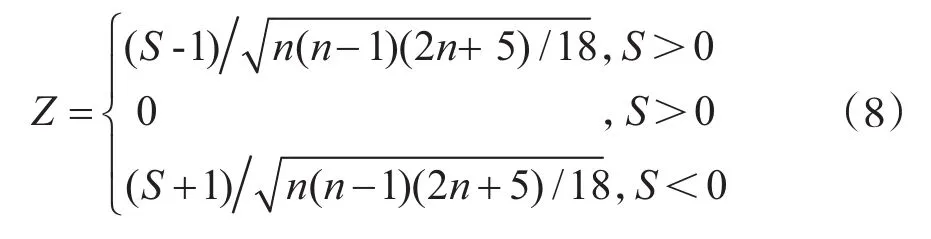
式中：

式中：

其中UF1=0，而UB的计算方法与UF类似，其为原时间序列逆序列的统计量。

累积距平法是根据曲线直观判断序列变化趋势的方法，对于序列X，t时刻的累积距平可以表达为[21]：

2 结果与讨论

2.1 降雨年内分配特征年际变化分析

淮阴站1951～2015年年内降雨分配不均系数、信息熵、集中度、集中期和重心的变化如图1所示。从图1可以看出，不均系数、信息熵、集中度、集中期和重心均呈现出较大的波动，其中不均匀系数最大值出现在1965年，最小值为1966年，信息熵最大值为1966年，最小值为1965年，两者表现正好相反；集中期、集中度、重心最大值出现年份均为1962年，最小出现年份分别为1966年、1966年、1973年，三者表现基本一致但略有差别。采用M-K方法分析淮阴站降雨年内分配各指标年际变化趋势，结果如表1所示。从表1中统计量Z可以看出，各指标均存在不显著变化趋势。不均匀系数、集中度、信息熵表征的年内分配不均匀性有降低趋势，重心、集中期表征的降雨集中时期有后移趋势，但从斜率β具体数值来看，其变化幅度均不大，表现较一致。采用M-K突变分析方法进一步绘制淮阴站降雨年内分配特征各指标UF和UB曲线如图2。从图2可以看出，各指标的UF、UB统计量存在多个交叉点但交叉点均在置信区间（-1.96，1.96）之内，表明淮阴站年内降雨分配特征各指标存在多个突变点，但UF变化均未突破显著性临界值，各指标均不存在突变现象。

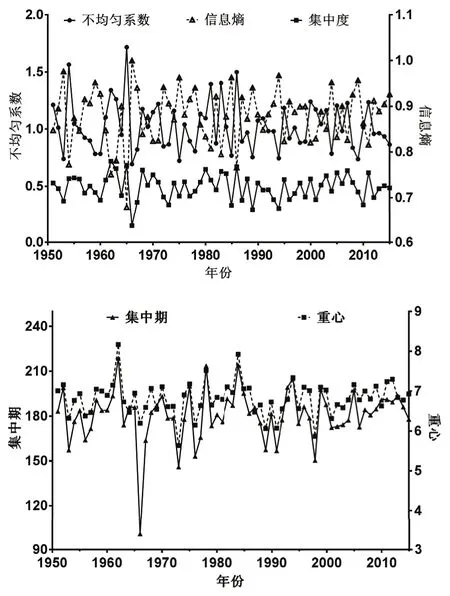
图1 淮阴站降雨年内分配特征变化

表1 淮阴站降雨年内分配特征M-K趋势检验

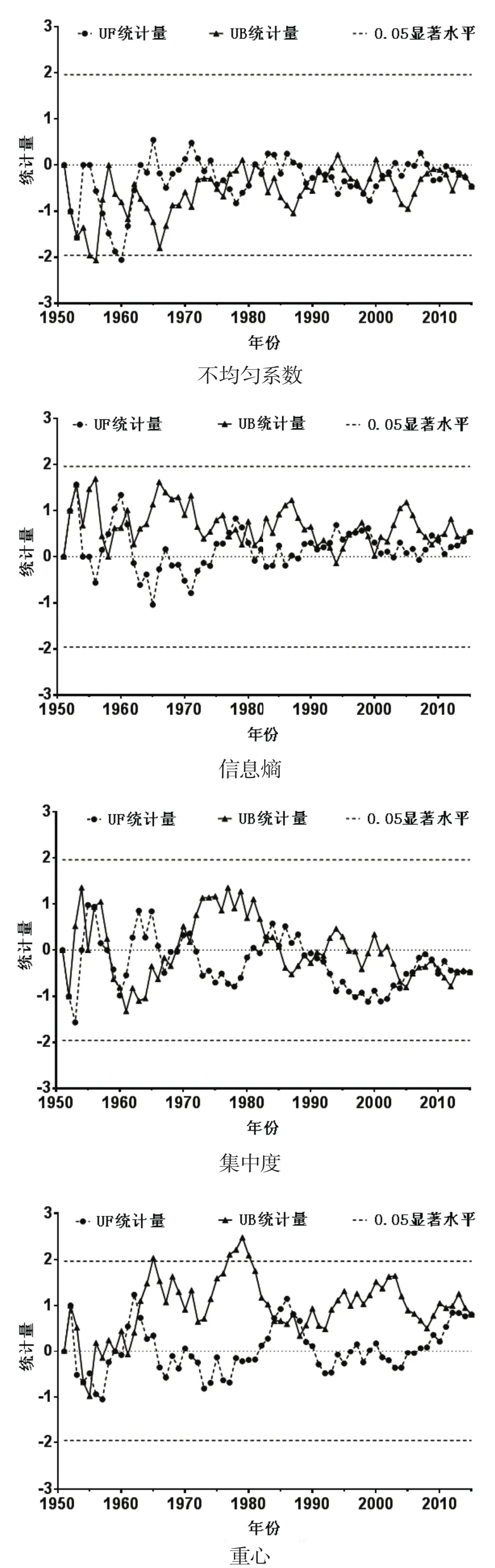
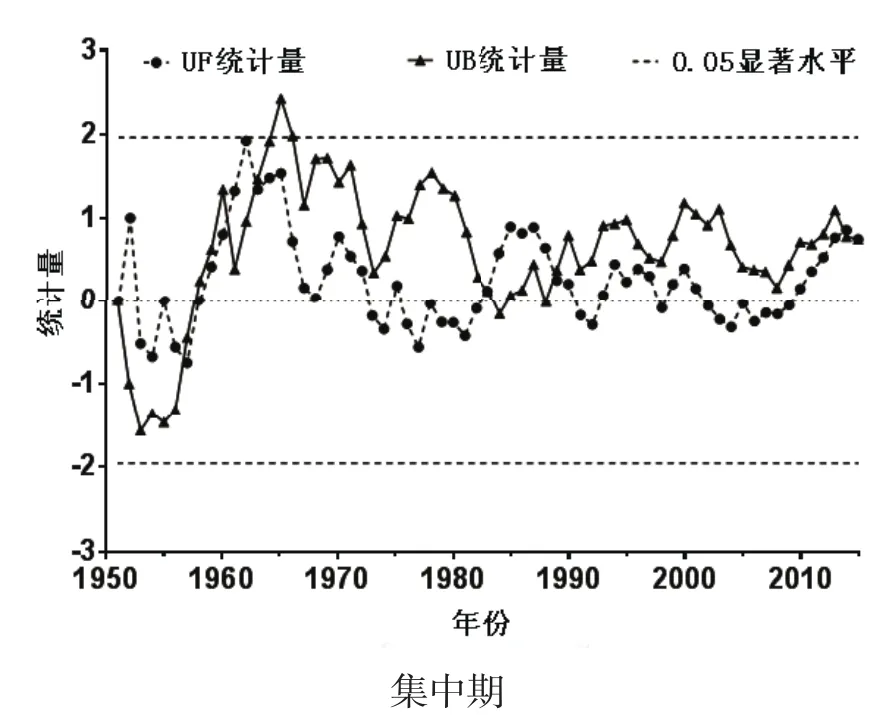
图2 淮阴站降雨年内分配特征M-K突变分析

2.2 降雨年内分配指数变化阶段性

为辨析年内降雨分配特征的变化阶段，采用距平累积法绘制淮阴站各指标的距平累积过程线（图3）。如图3所示，淮阴站年内分配不均性系数、信息熵、集中度总体存在着4个变化阶段：1951～1960年、1961～1978年、1979～1999年、2000～2015年，其中1961～1978年、1979～1999年是2个完整的上升下降或下降上升周期，其历时分别为18年、21年。集中期、重心总体存在3个变化阶段：1951～1962年、1963～1986年、1987～2015年均为较完整的下降上升周期，其历时分别为12年、24年，29年，其周期历时有逐渐增大的趋势。年保证率存在3个历时2年以上较低保证率时段：1962～1965年、1969～1972年、2005～2008年；存在3个历时2年以上的较高保证率时段：1966～1968年、1982～1989年（除1986年）、1992～1995年，总体呈现出丰枯交替变化。

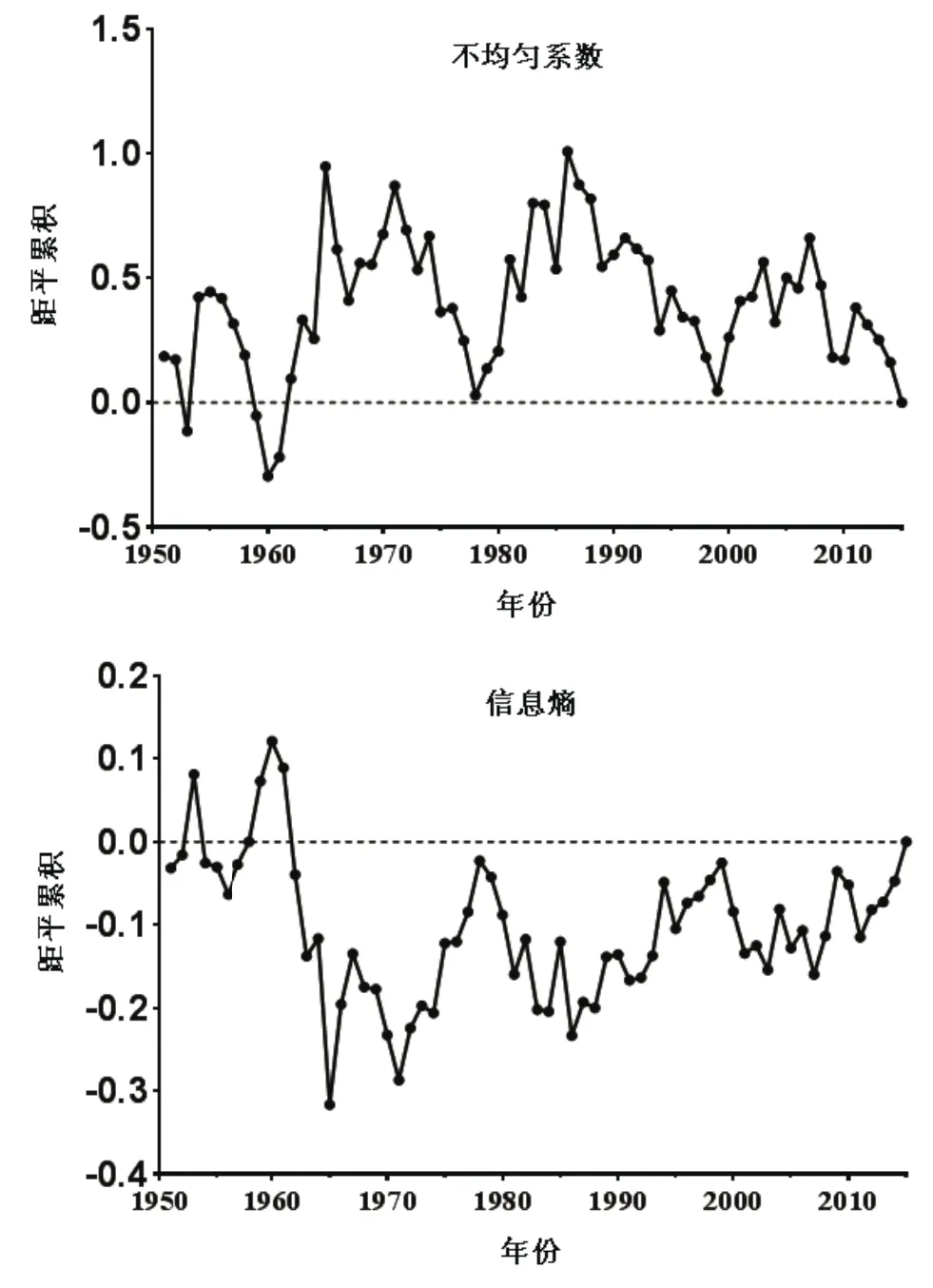
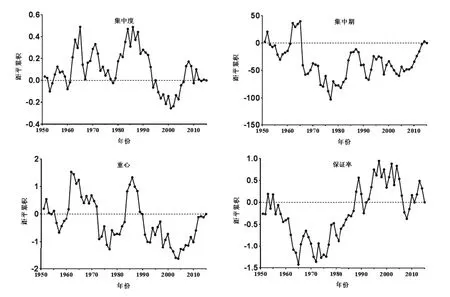
图3 淮阴站降雨年内分配特征距平累积曲线

2.3 降雨年内分配指标相关性分析

淮阴站1951～2015年降雨年内分配特征各指标的Pearson相关系数计算结果如表2所示。从表2可以看出，不均匀系数与集中度高度正相关，与信息熵高度负相关，与保证率显著负相关；重心与集中期高度正相关，与集中度低度相关；集中度与信息熵高度负相关，与保证率显著负相关，与集中期低度正相关；信息熵与保证率显著正相关。可见，不均性系数、集中度和信息熵表征基本是一致，重心与集中期的表征也是一致的，年内降雨分配的不均匀系数、集中度和信息熵与年降雨保证率具有一定关联，但重心和集中期与年降雨保证率关联不大。

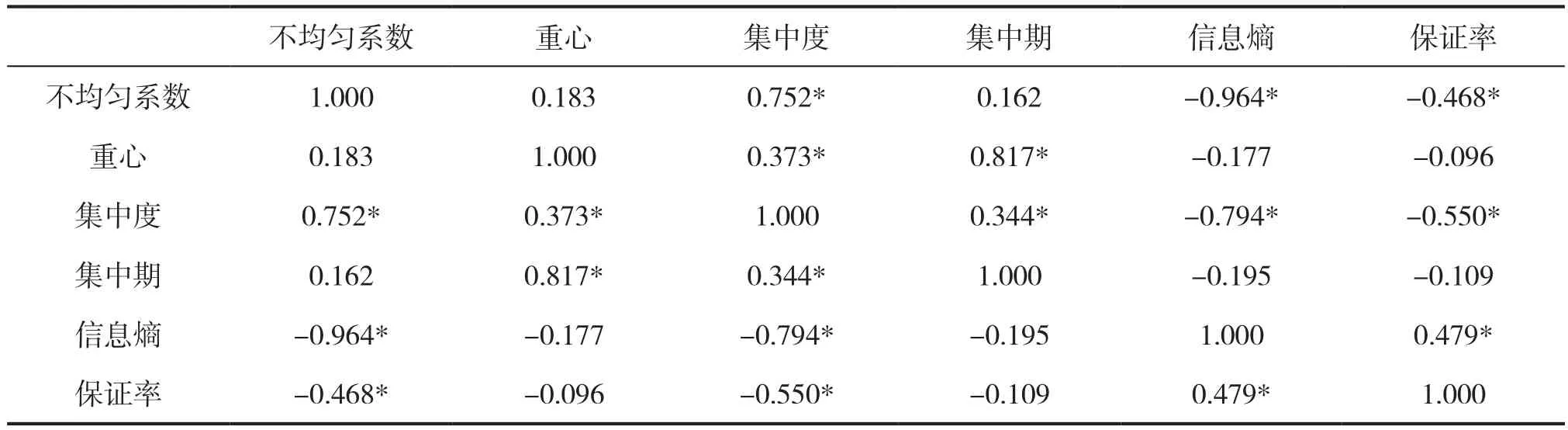
表2 相关系数矩阵

3 结论

（1）淮阴站降雨年内分配不均匀性总体表现出逐年递减的趋势，降雨集中期和重心都有后延的趋势，未通过显著性检验，且变化幅度较小，不均匀系数、信息熵、集中度的趋势变化率不足0.01/10年，年降雨保证率有逐年上升的趋势，约为10年上升一个百分点，各指标均未出现明显的突变。

（2）淮阴站年内分配不均性系数、信息熵、集中度总体存在着4个变化阶段，2个完整的上升下降或下降上升周期；集中期、重心总体存在3个变化阶段，均为较完整的下降上升周期；年保证率总体呈现出丰枯交替变化。

（3）年内分配不均匀系数、集中度、信息熵之间存在着高度相关关系，具有互通性；重心与集中期高度正相关，具有互通性；不均匀系数、集中度、信息熵均与保证率存在着显著相关关系，而重心、集中期与保证率相关性不大。