页岩气水平井增产改造体积评价模型及其应用
任 岚 林 然 赵金洲 荣 莽 陈建达
1.“油气藏地质及开发工程”国家重点实验室·西南石油大学 2.中国石化江汉油田分公司石油工程技术研究院
0 引言
页岩气储层渗透率极低,需要通过水平井分段分簇缝网压裂增产,从而显著提高页岩气井产量[1-2],目前该增产技术已经成为国内外页岩气田实现商业化开采的核心增产技术[3-4]。水平井缝网压裂实施过程中,多条水力裂缝同时延伸,并激活附近储层中的天然裂缝群,交织组成复杂的高导流裂缝网络,形成储层改造体积(SRV)[5],进而显著提升页岩储层表观渗透率,大幅提高页岩气井压后产量[6-7]。
准确表征SRV形态和体积对于页岩气藏水平井分段多簇的缝网压裂前期设计和后期评估都具有非常重要的指导作用[8-9]。目前,SRV评价方法主要包括微地震监测法[10-15]、倾斜仪测量法[16-22]以及数学模型计算法。其中,数学模型计算法主要包括解析模型[23-25]和离散裂缝网络模型[26-32]。直接测量的微地震监测法较为可靠,但成本高昂,而倾斜仪测量法虽成本较低,但精度不理想,应用受限;数学模型方法的解析模型只考虑了压裂时储层流体压力变化触发岩石破坏的改造区描述,忽略了应力场变化的影响,模型应用时需要采用微地震数据进行校正;离散裂缝网络模型涉及大量的裂缝延伸模拟计算,计算速度较慢,耗时较长。由于理论模型计算SRV可以降低工程成本,发展和完善SRV评价理论模型,提高计算的准确性和可靠性具有重要意义。
页岩储层基质渗透率极低,通常仅为纳达西级别[33-35],但页岩脆性较高,往往发育大量的天然裂缝,可以改变缝网压裂过程中的SRV形成过程,进而影响压裂增产效果[36-39]。提出的模型假设储层天然裂缝系统和基质共同控制流体扩散和流体场分布[40-41],同时计算多簇水力裂缝起裂延伸引起的地层应力变化[42-43],建立了考虑水力压裂时储层内流体压力升高和分簇裂缝间的应力干扰效应共同作用触发天然裂缝破坏从而形成SRV的理论计算模型。
1 数学模型建立
基于页岩压裂过程中水力压裂延伸导致的地层应力场变化以及压裂液滤失引起的储层压力场抬升,判断水力裂缝附近天然裂缝的破坏状态和类型,即可对SRV进行计算和表征。因此,SRV数学模型将主要针对分簇裂缝延伸行为、水力裂缝诱导应力场变化、水力压裂储层压力场抬升以及天然裂缝破坏区域的扩展进行数值模拟与表征。
1.1 裂缝分段分簇扩展模型
在页岩气分段分簇压裂时,多条水力裂缝将同时从不同射孔簇起裂并延伸,如图1所示。
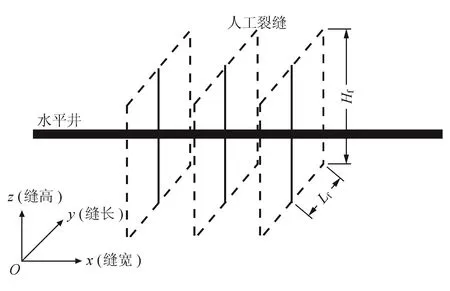
图1 页岩水平井分段分簇(单段3簇)缝网压裂裂缝扩展示意图
裂缝长度上任意点的水力裂缝最大宽度为:
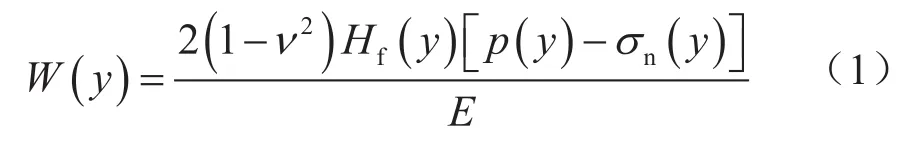
式中W(y)表示延伸路径上y处的最大缝宽,m;ν表示岩石泊松比;Hf(y)表示y处裂缝缝高,m;p(y)表示y处缝内流体压力,MPa;σn(y)表示y处作用有水力裂缝面的正应力,MPa;E表示岩石弹性模量,MPa。
Lamb[44]提出的椭圆剖面裂缝流动方程为:
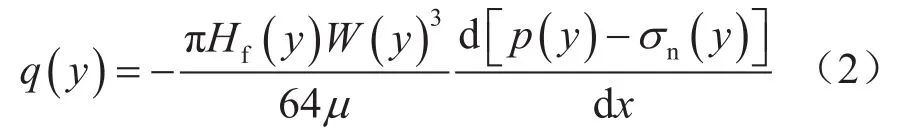
式中q(y)表示任意点y的流量,m3/min;μ表示注入的液体黏度,mPa·s。
基于裂缝内流体物质平衡原理[45],在长度方向上任意水力裂缝微元内压裂液流量应该等于裂缝微元体积变化量与压裂液滤失量之和:
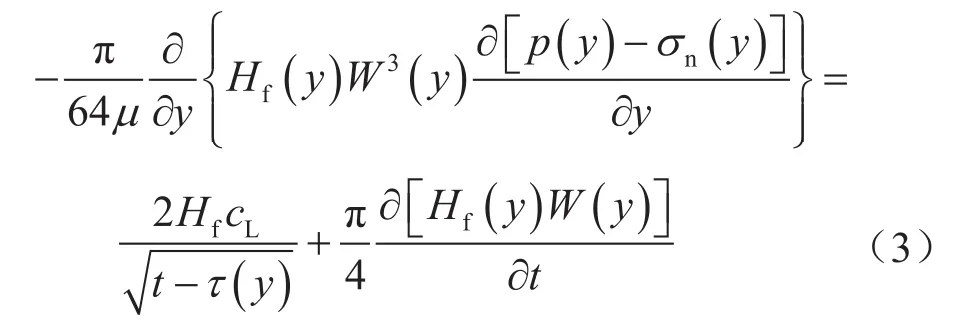
式中cL表示压裂液滤失系数,m/min0.5;t表示作业注入时间,min;τ(y)表示水力裂缝y处压裂液开始滤失时间,min。
水力裂缝延伸高度主要取决于岩石断裂韧性与缝尖应力强度因子,其中,缝尖应力强度因子与裂缝内流体压力和地层应力的关系式为:
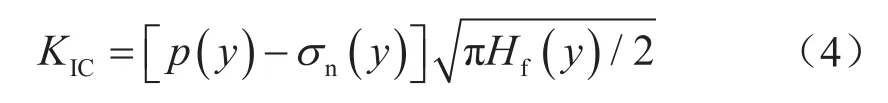
式中KIC表示页岩岩体的断裂韧性,Pa·m0.5。
求解边界条件:
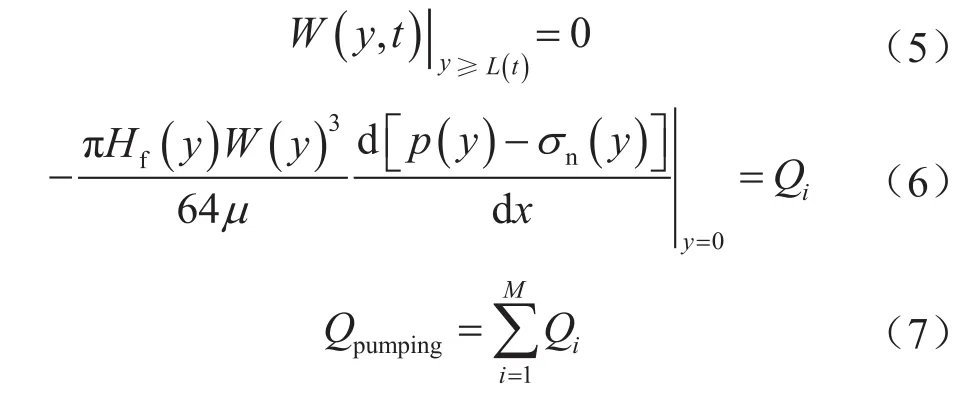
式中Qi表示任意的i条裂缝分配的流量,m3/min;Qpumping表示压裂施工泵注总排量,m3/min;M表示射孔簇数,即裂缝条数。
式(1)~(4)中,共同包含了4个未知变量(p、Hf、W、q),代入求解条件式(5)~(7),通过划分动态网格,采用隐式有限差分法,即可对未知量进行耦合求解。其中,首先设定某一时间步长内的裂缝延伸长度,赋予缝内压力初值,代入缝宽和缝高方程中计算裂缝开度和高度,并分别给基于裂缝流动方程与连续性方程,采用Picard循环迭代法(学习系数取值0.2)确定裂缝延伸长度与缝内压力分布。
1.2 水力裂缝诱导应力场
根据线弹性理论中的Griきth模型,可推导出水力裂缝附近的诱导应力方程[46],即
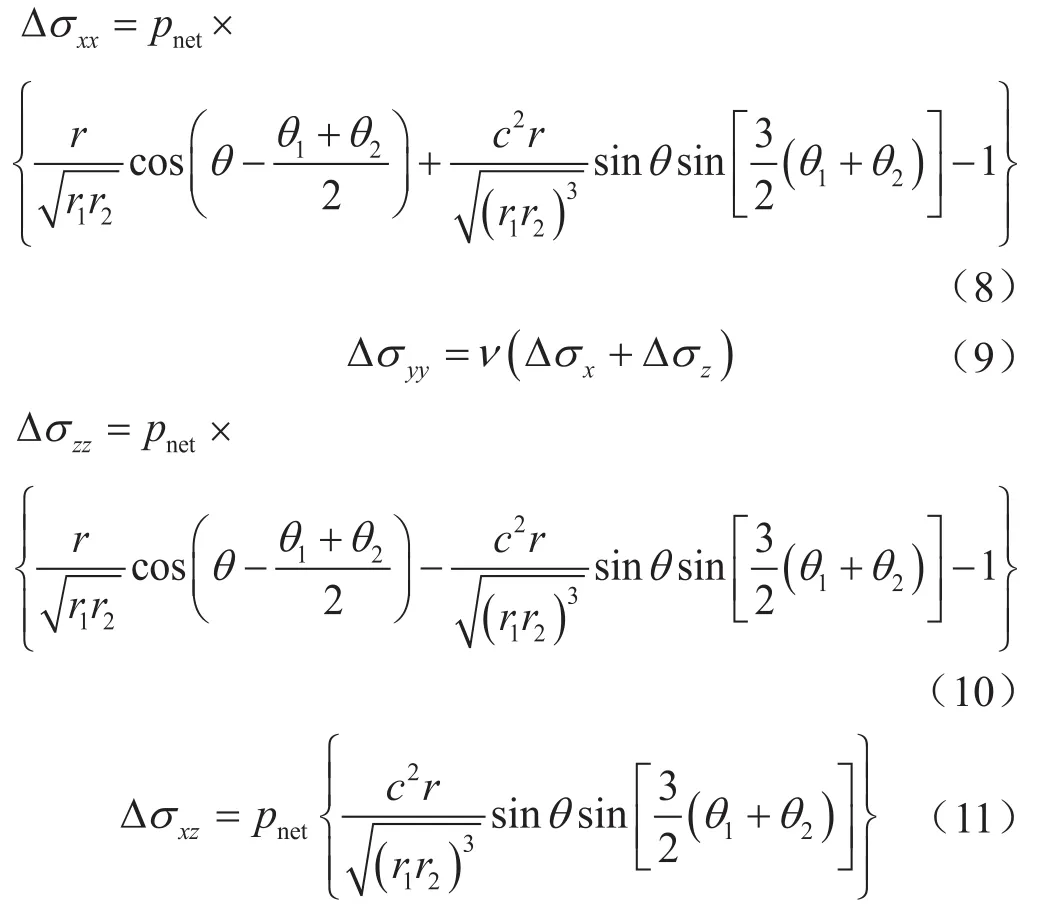
式中 、 、 分别表示x、y、z方向上法向诱导应力,MPa; 表示x面上z方向切向诱导应力,MPa;pnet表示裂缝内净压力,MPa;c表示裂缝高度hf(x)的 1/2,m ;r1、r2、θ1、θ2分别表示几何参数,可由图2中几何关系求得,m。
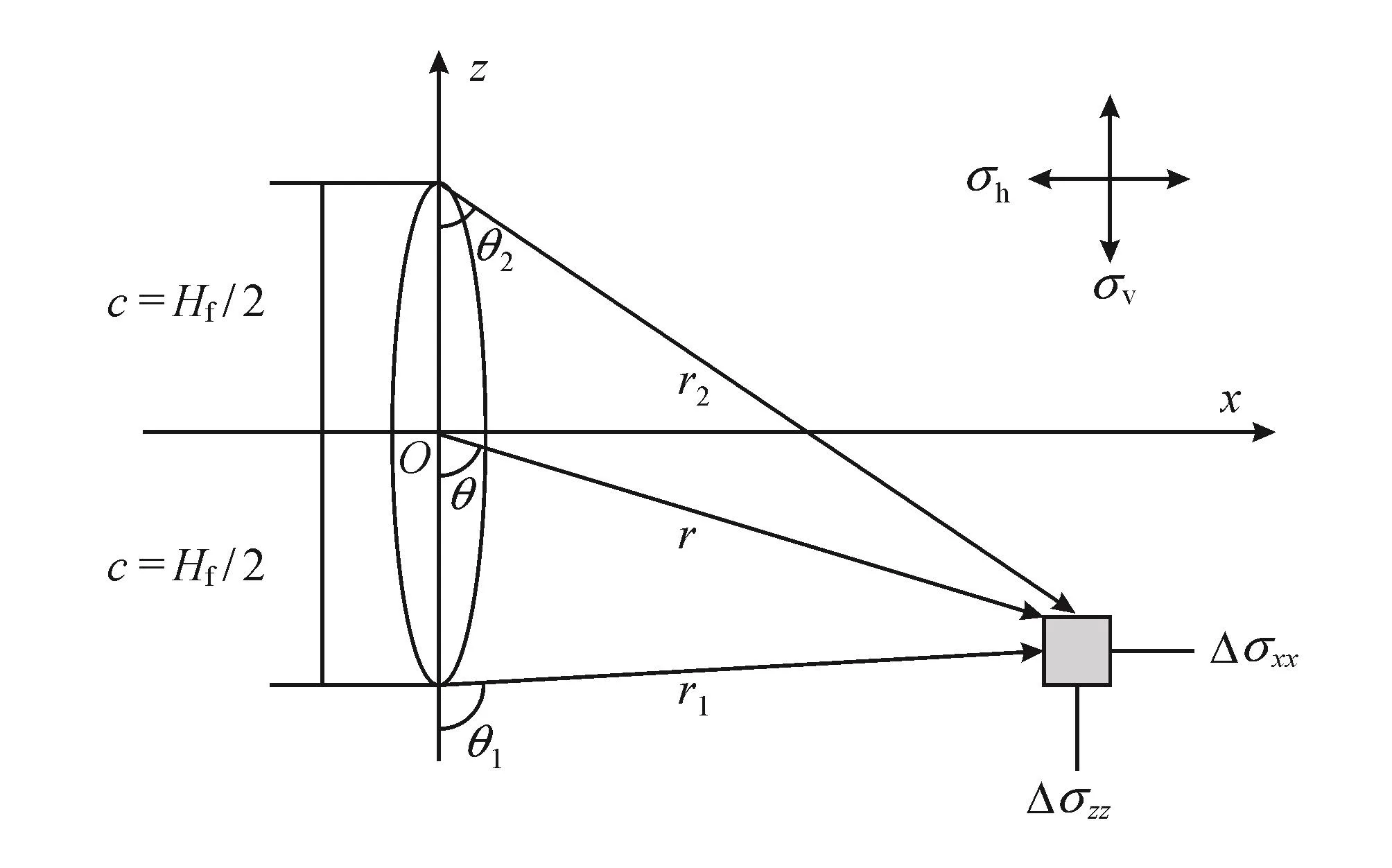
图2 水力裂缝附近诱导应力计算示意图
原始地层应力与水力裂缝引起的诱导应力都为三维二阶张量,通过两者各分量的线性叠加,即可计算得到页岩水平井分段分簇压裂过程中的地层应力场分布,即
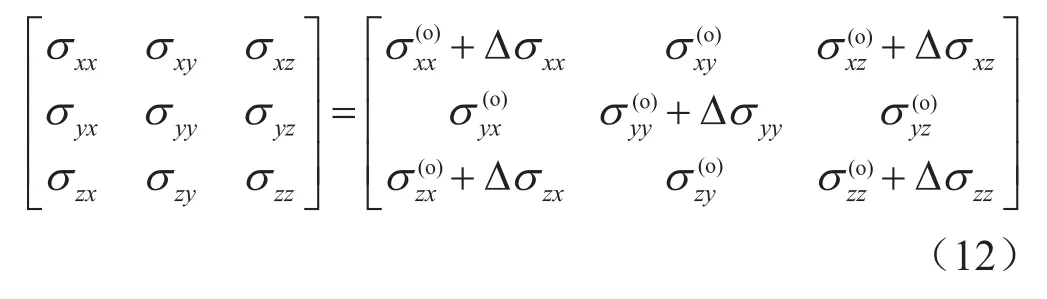
1.3 水力压裂储层压力场
页岩气水平井缝网压裂时,由于施工规模较大,大量压裂液将从水力裂缝壁面滤失流入附近储层中,抬高储层压力场。因此,可以基于水平压裂井储层渗流模型(图3),并将水力裂缝视作面源,计算储层压力变化情况。
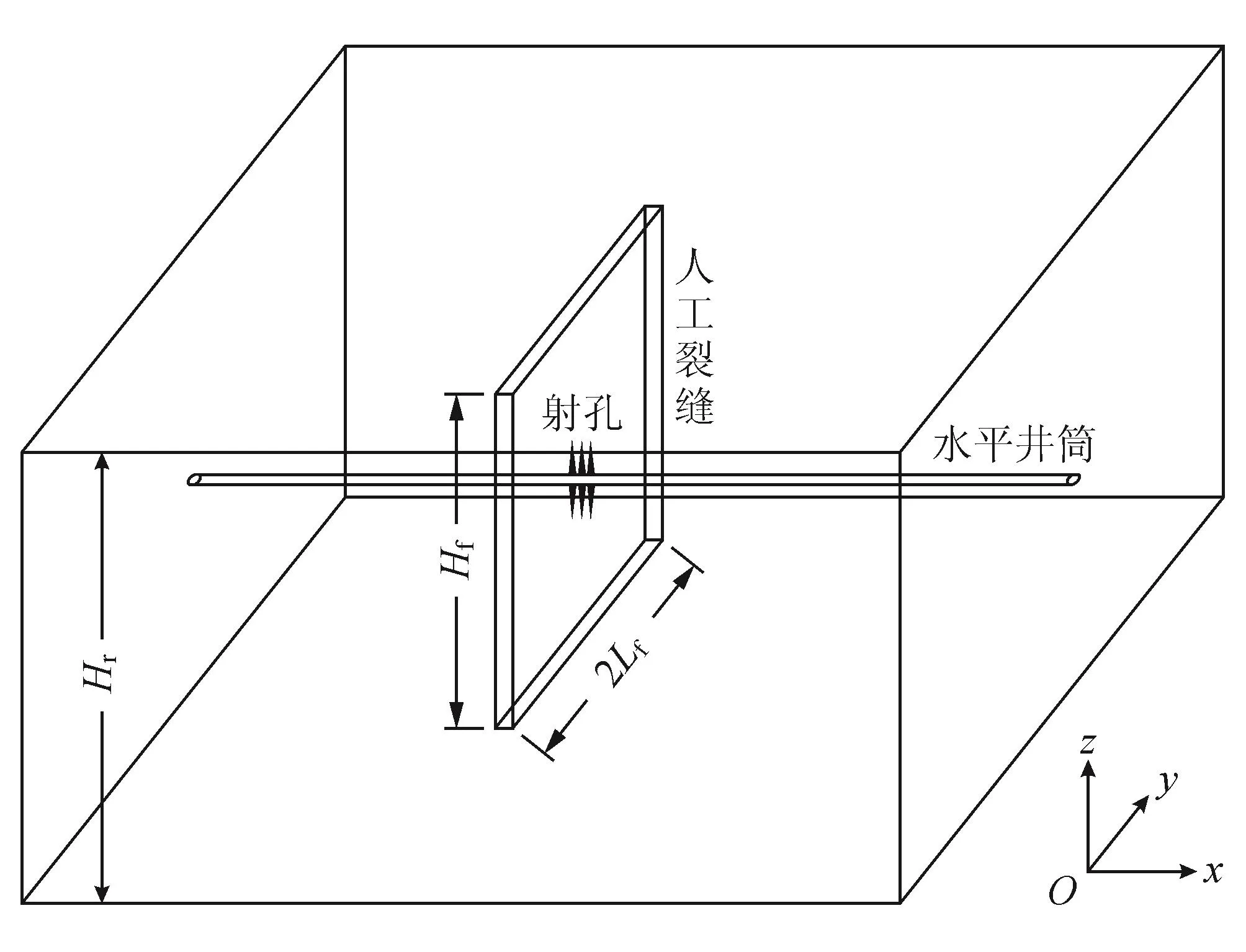
图3 水平井压裂的储层压力计算模型图
通过格林源函数(Green Function)方法与Laplace变换[47],推导得出水平井压裂滤失时,Laplace域内任意空间位置处的储层流体压力增值为:
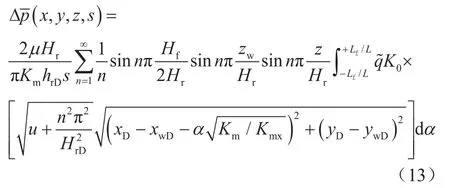
通过式(13)计算出Laplace域内储层压力值后,再通过Stehfest数值反演[48]算出储层内任意位置和时间的实际压力值:
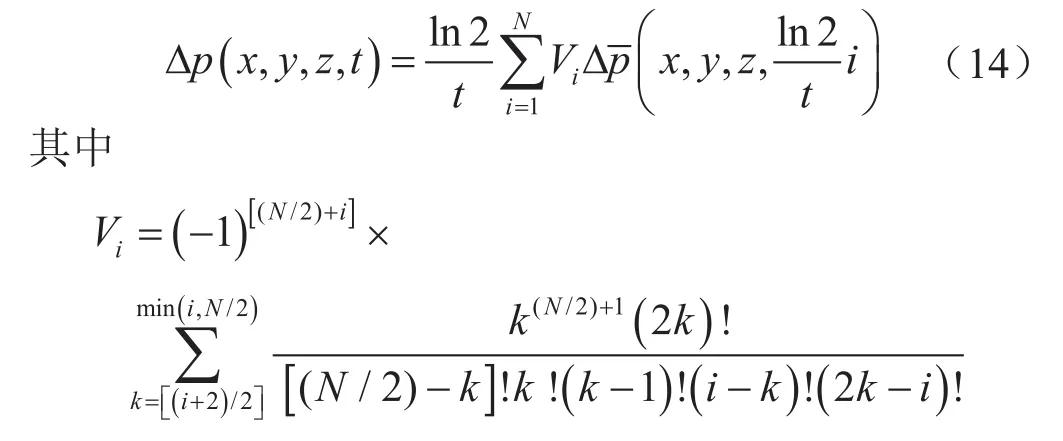
式中N表示求和项数,值越大越精确,一般取6~18之间的偶整数。
储层压力场为标量场,和地层应力场类似,当储层中存在多条水力裂缝时,能够通过线性叠加运算,计算出当前储层内任意点任意时刻的压力值:
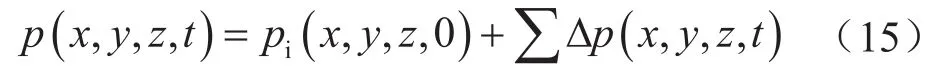
式中pi表示初始储层压力场,表示储层压力增量叠加场,MPa;p表示当前储层压力场,MPa。
1.4 天然裂缝破坏判断方程
页岩通常脆性较高,往往发育有大量的天然裂缝,并且天然裂缝具有较强的方向性。缝网压裂时,天然裂缝受到地层应力改变和储层压力抬升的双重影响会发生张性破坏或剪切破坏,被激活形成储层改造体积[2]。基于张量运算准则,对地应力条件下的天然裂缝避免进行受力分析(图4)。根据Warpinski准则[49],建立任意产状天然裂缝的破坏判断准则。
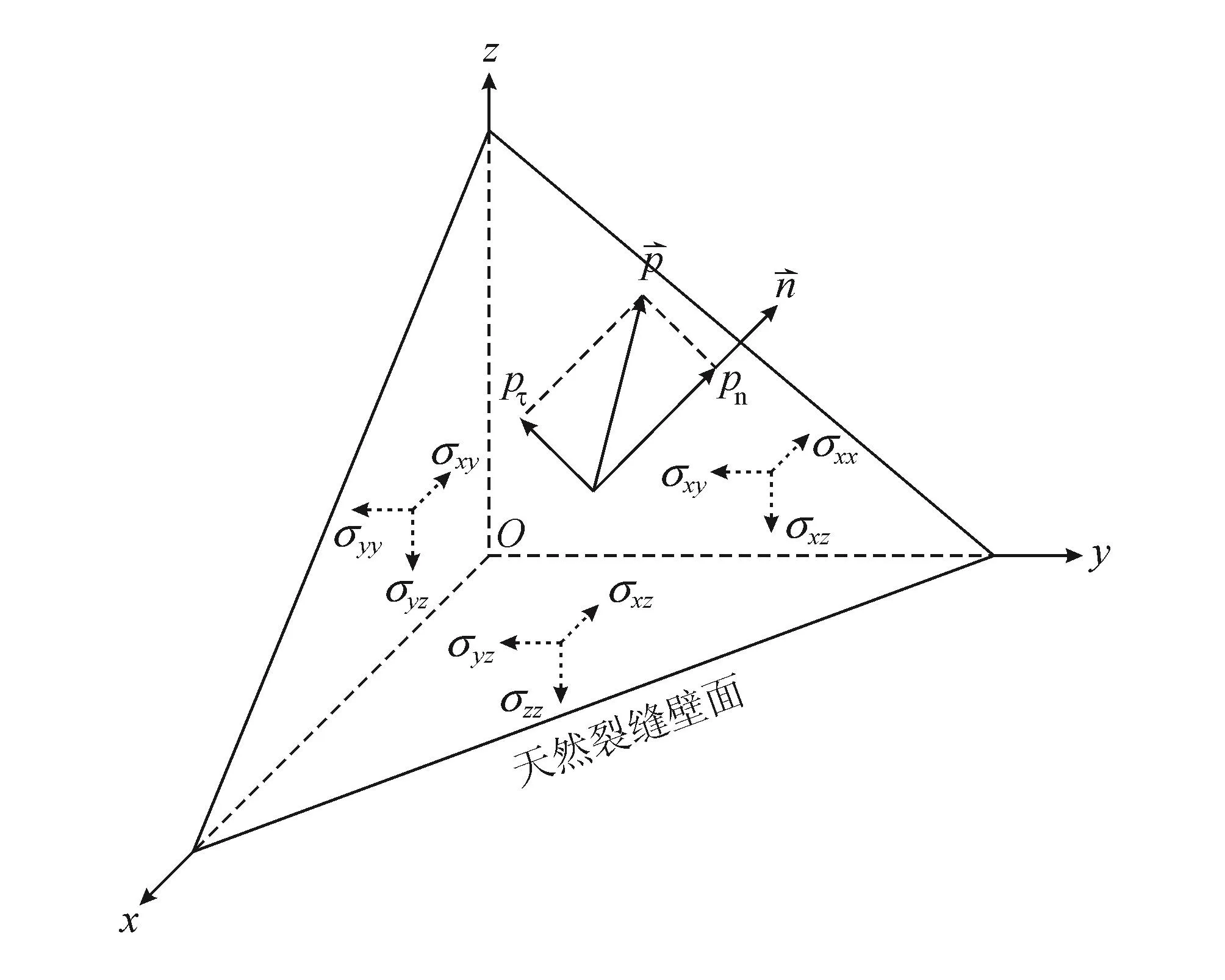
图4 天然裂缝壁面受力分析图
作用在天然裂缝面上的力为:
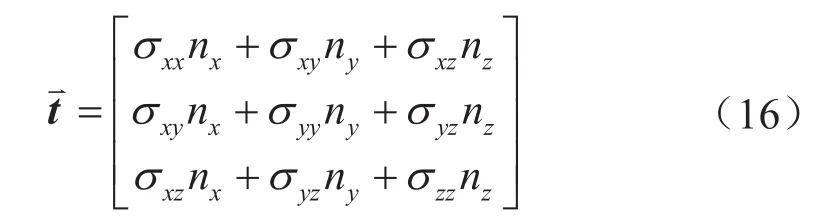
将式(16)中计算得到的作用力分解到天然裂缝壁面法向上,得到裂缝壁面所受到的法向应力(正应力)值:
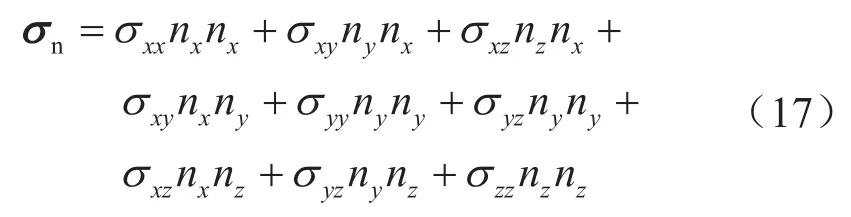
式中 表示裂缝壁面受到的正应力值,MPa。
基于矢量计算原则,天然裂缝壁面所受剪切方向的应力分量值为:
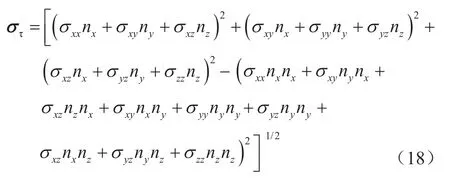
根据Warpinski准则可知,当天然裂缝内流体压力超过其壁面所受正应力值与抗张强度之和的情况下,天然裂缝就会发生张性破坏,故其张性破坏判别式为:

式中pnf表示天然裂缝内压力,即其所在位置的储层压力,MPa;σn表示天然裂缝壁面所受法向应力(正应力)值,MPa;St表示抗张强度(天然裂缝),MPa。
天然裂缝在满足下式条件下将发生剪切破坏,即
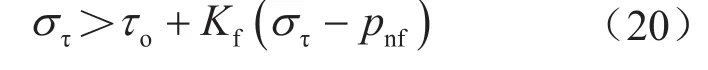
式中στ表示天然裂缝壁面所受应力(剪切应力)值,MPa;τo表示天然裂缝内聚力,MPa;Kf表示天然裂缝壁面摩擦系数,无量纲。
1.5 SRV计算流程
SRV计算流程:①基于井筒位置与分段射孔参数建立相应的三维笛卡尔坐标系;②利用式(1)~(7)模拟计算裂缝扩展,获得延伸裂缝的几何尺寸、缝内压力和流量分布;③基于分簇裂缝延伸模型,耦合求解出裂缝延伸过程中各参数,并通过式(8)~(12)计算出诱导应力场和地层应力场;④基于水力裂缝几何参数及其滤失参数,通过式(13)~(15)计算出储层压力场;⑤对水力裂缝周围区域的任意位置点,考虑该点的应力场和压力场数据,利用式(16)~(20)判断天然裂缝发生破坏与否;⑥根据储层中破坏的天然裂缝空间位置坐标,并结合三维数值积分方法,分别计算得到发生剪切破坏与发生张性破坏的体积,对这两个破坏体积求并集,最终计算得到储层改造总体积。
2 模型验证与应用
2.1 模型验证分析
基于国内西南地区FL页岩示范区气藏X1-HF井压裂施工数据和压后微地震监测数据,使用本文所建立的数学模型对该井缝网压裂时形成的SRV进行模拟计算,相关地质与工程参数如下:原始储层压力为38 MPa,基质系统孔隙度为0.051,天然裂缝系统孔隙度为0.021,基质系统渗透率(x、y、z方向)分别为 0.50 μD、0.50 μD、0.05 μD,天然裂缝系统渗透率(x、y、z方向)分别为25 mD、 50 mD、5 mD,储层综合压缩系数为4.00×10-4MPa-1,水平最大地应力为61.50 MPa,水平最小地应力为52.40 MPa,垂向地应力为58.50 MPa,天然裂缝的黏聚力为1.00 MPa,天然裂缝的抗张强度为0.50 MPa,天然裂缝面摩擦系数为0.4,天然裂缝与主应力方向夹角(逼近角)为37°,裂缝倾角为62°,杨氏模量为30 GPa,泊松比为0.26,储层厚度为300 m,压裂液黏度为10 mPa·s,泵入排量为13 m3/min,泵注时间为2 h,簇数为3,簇间距为30 m。根据模型数值计算得出,当该段压裂施工结束时,储层流体压力分布计算结果如图5所示。页岩水力压裂过程中,受滤失效应的影响,流体压力在储层中传播,使得储层的压力显著上升,其压力分布呈不规则的“倒漏斗”形状。
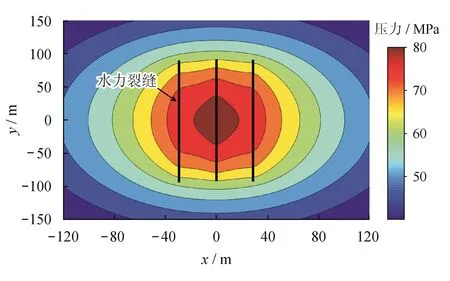
图5 储层压力分布图
压裂后地层应力分布情况如图6所示,从图6中可知,受延伸裂缝诱导应力的影响,导致裂缝间的应力变化较大,而裂缝外部应力变化相对较小。
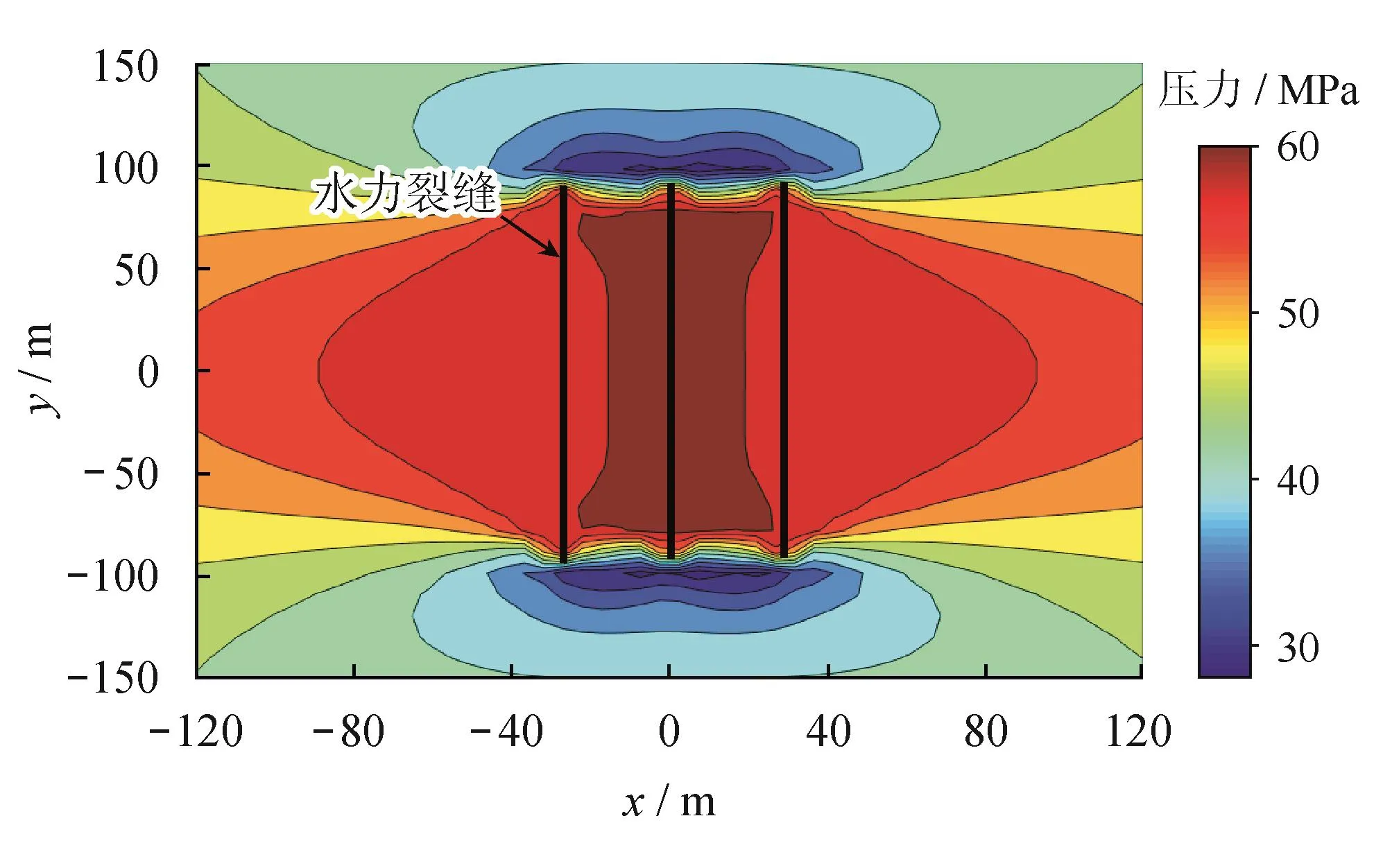
图6 地层x—y截面上σx分布图
水平井该段实施水力压裂后,附近地层应力分布如图6所示。可以看出,水力裂缝附近产生了明显的诱导应力,引起各条裂缝之间地应力值显著增大,但裂缝外侧区域内地应力变化相对较小。因此,水力裂缝之间区域内受到的应力干扰效应更强,更容易发生天然裂缝破坏。
计算得到该段总体SRV为2.03×106m3,其空间展布形态如图7所示。因为该地层中的天然裂缝是存在一定倾角的高角度缝,对滤失渗流存在一定的各向异性影响,从而导致SRV形态出现非轴对称的“倾斜”现象。
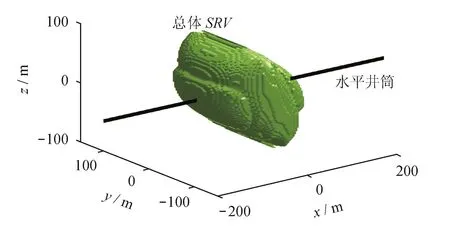
图7 该压裂段总体SRV空间形态展布图
为了对本文所建立的SRV评价模型进行可靠性验证,将计算所得总体SRV轮廓面与该段压裂现场实际监测到的微地震数据点置于同一坐标系中进行匹配比较(图8~11)。
从图8~11可见,总体上微地震监测结果与理论计算结果匹配较好,在水平面(x—y截面)和裂缝长度方向的纵剖面(y—z截面)上匹配程度高,在水平井筒方向上的纵剖面(x—z截面)匹配较差。

图8 三维SRV轮廓面与微地震信号匹配图
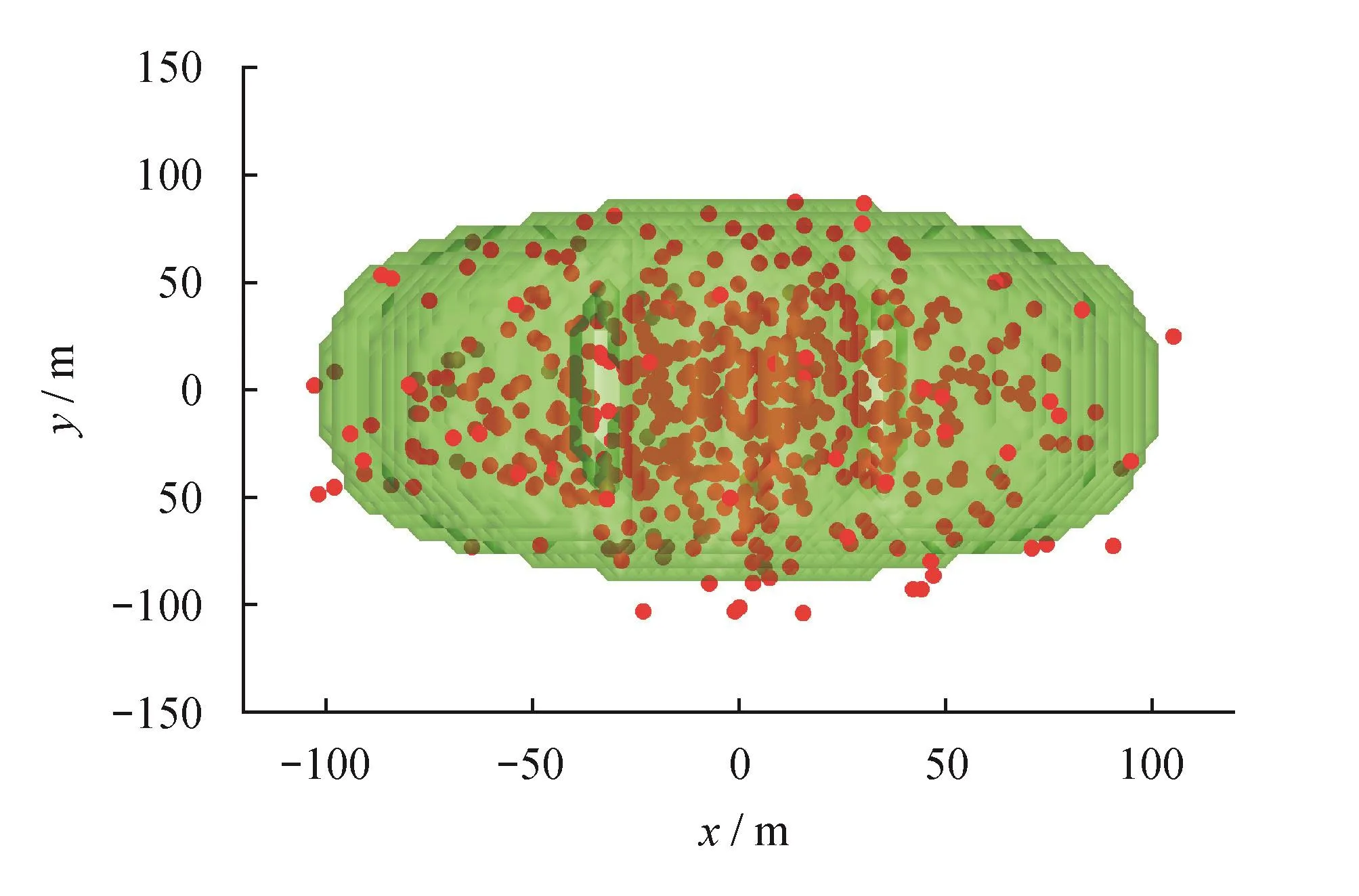
图9 SRV轮廓线与微地震信号匹配图(x—y截面)
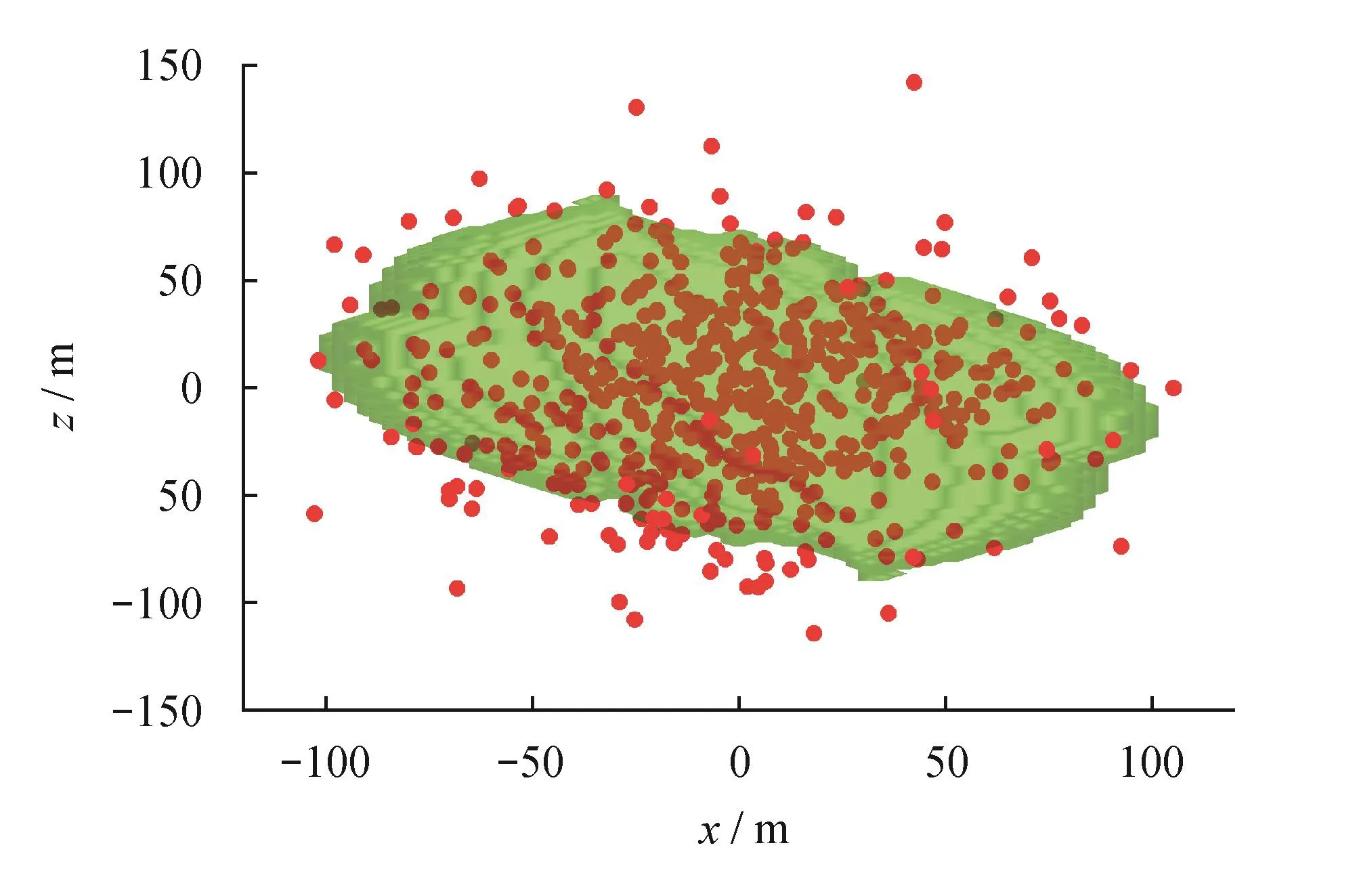
图10 SRV轮廓线与微地震信号匹配图(x—z截面)
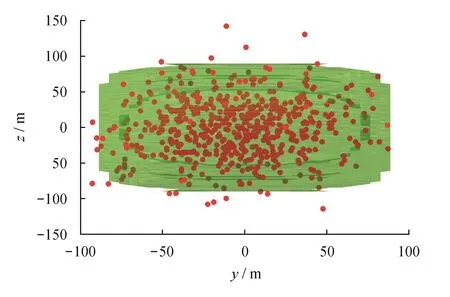
图11 SRV轮廓线与微地震信号匹配图(y—z截面)
通过数据统计,92.6%的微地震信号分布在SRV轮廓面之内,7.4%的微地震信号分布在SRV轮廓面之外,这主要是受压裂过程水力裂缝远界天然裂缝的随机破坏导致微地震监测结果和理论模型的计算产生的差异,同时还受到流体场传播和应力场干扰范围影响,导致理论计算的SRV较微地震监测的SRV偏小。总体上所建模型计算所得SRV轮廓面与实际微地震监测区匹配程度较高,且能很好匹配微地震产生的非对称SRV体积,证实了其较高的可靠性和准确性。
2.2 模型矿场应用
采用建立的SRV评价模型,对FL页岩气示范区93口井进行了SRV计算,并结合示范区地质模型,对各井SRV展布进行了三维可视化表征。现以FL页岩气示范区内X2-HF井为例进行计算。
该井位于FL页岩气示范区北部构造高部位,水平井平均垂深约为2 560 m,水平段长约为1 470 m,其目标储层为上奥陶统五峰组—下志留统龙马溪组,储层内高角度的天然裂缝较为发育。地层的垂向应力是63.50 MPa,最大水平主应力是58.50 MPa,最小水平主应力是52.50 MPa,地层岩石泊松比为0.23,杨氏模量为34.5 GPa。该井实施了分段分簇大型加砂压裂施工,设计分段15段,单段射孔簇数3簇,压裂液主要选用滑溜水,总用量28 650 m3,支撑剂主要选用100目粉陶、40/70目覆膜砂以及30/50目覆膜砂,施工压力45~65 MPa,泵注排量12~14 m3/min。该井各段分簇压裂具体施工参数如表1所示。
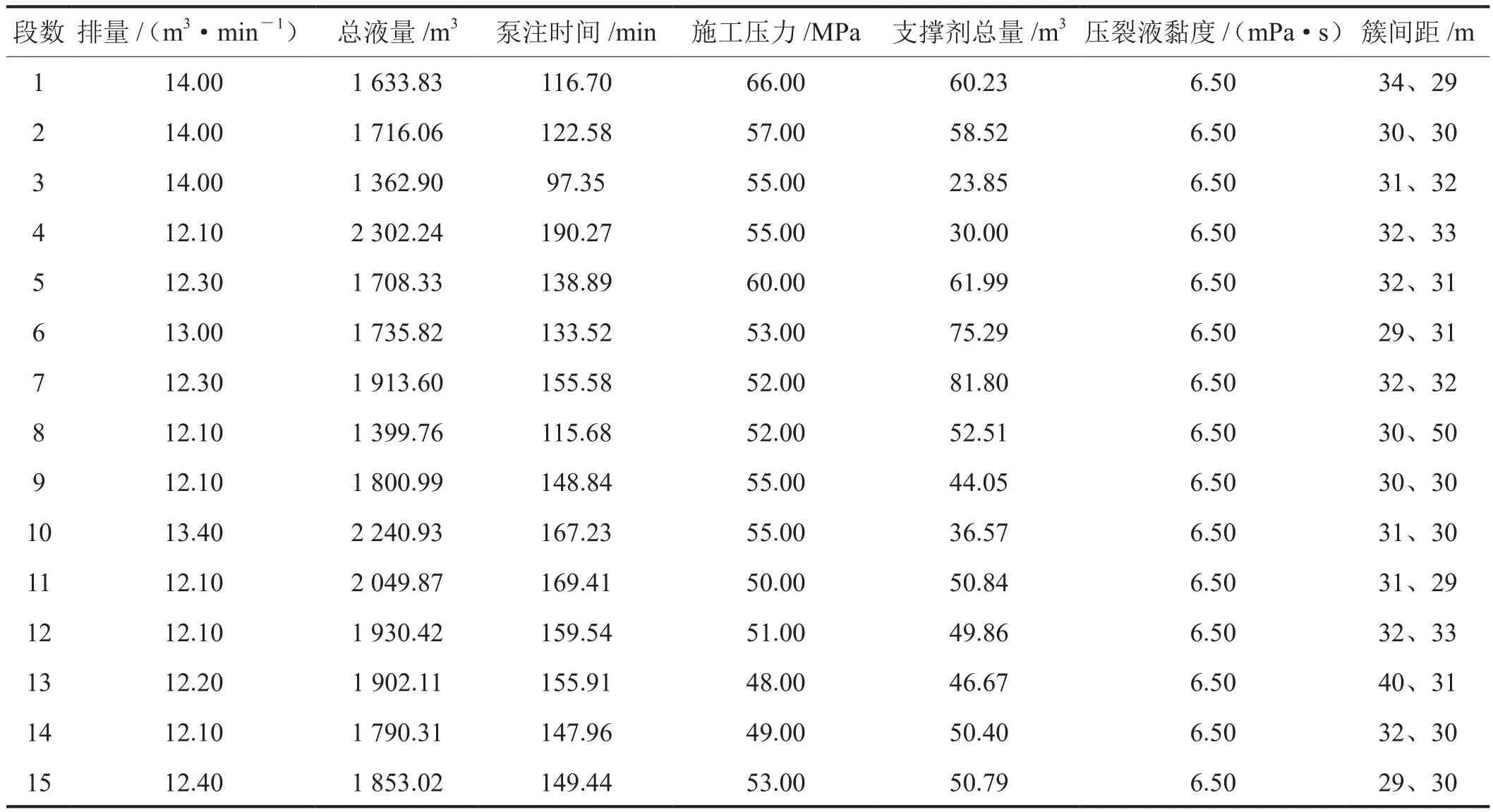
表1 FL页岩气示范区X2-HF井压裂施工参数表
基于页岩压裂SRV评价模型,结合表1中的矿场实际压裂施工数据,通过SRV评价模型计算程序得到X2-HF井各段压裂后形成的储层改造体积参数(表 2)。
将X2-HF井全井段压裂SRV空间数据点嵌置于示范区地质模型中,并把SRV三维展布情况进行可视化呈现,其效果如图12所示。
X2-HF井压裂单段SRV的长、宽、高平均分别为334 m、101 m和75 m,平均体积1.53×106m3;全井段SRV总体积为24.5×106m3。由全井段SRV三维展布图可知,X2-HF井储层得到了充分改造,该井投产后进行的产能测试表明其压裂增产效果较为显著,无阻流量达到了81.9×104m3/d。
对FL页岩气示范区内共计93口压裂水平井进行了SRV计算和表征,计算结果统计与SRV展布情况分别如图13、14所示。计算结果统计表明,FL页岩气示范区内单井SRV集中分布在20×106~40×106m3之间,大部分井改造体积较理想。但由图14的SRV整体展布平面图可以发现,部分井组之间仍存在较大的未改造区,其中宽度大于250 m的未改造区占比达到了34%,可通过在这些井组间设计加密井措施提高储层总体改造程度和有效动用,从而提高FL页岩气示范区的经济开发效益。
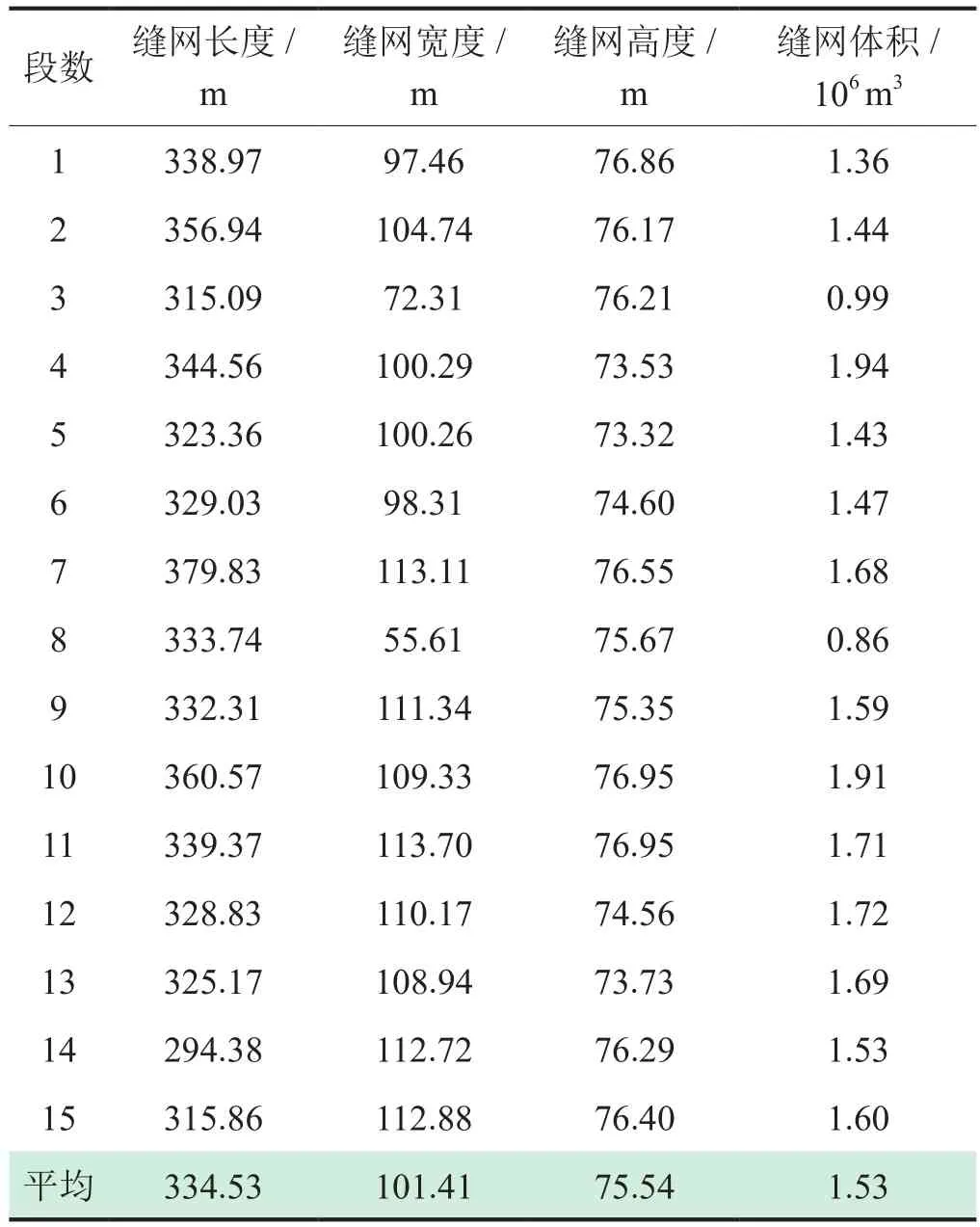
表2 FL页岩气示范区X2-HF井各段SRV参数表
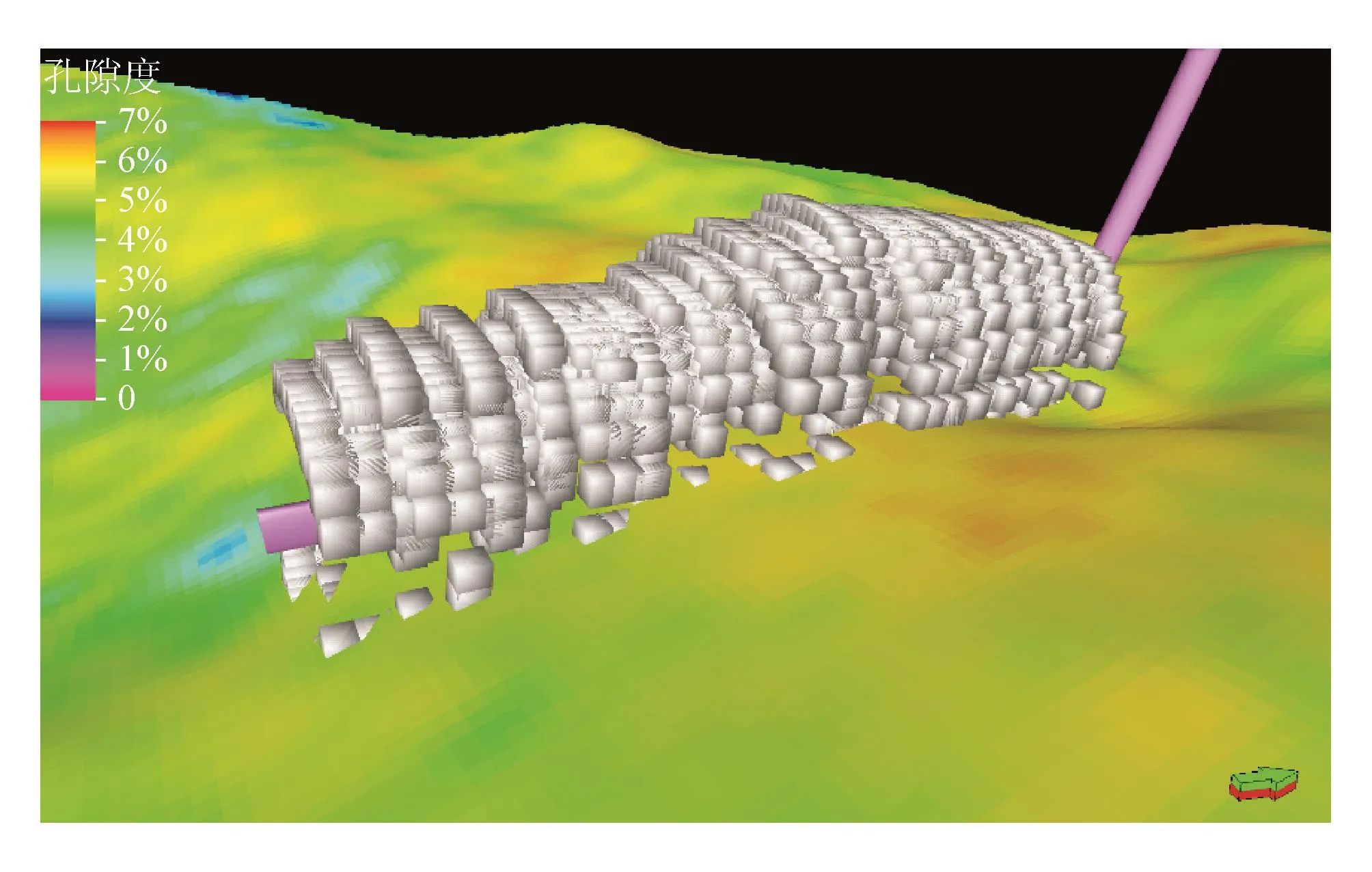
图12 全井段SRV在地质模型(孔隙度)中的三维展布情况图
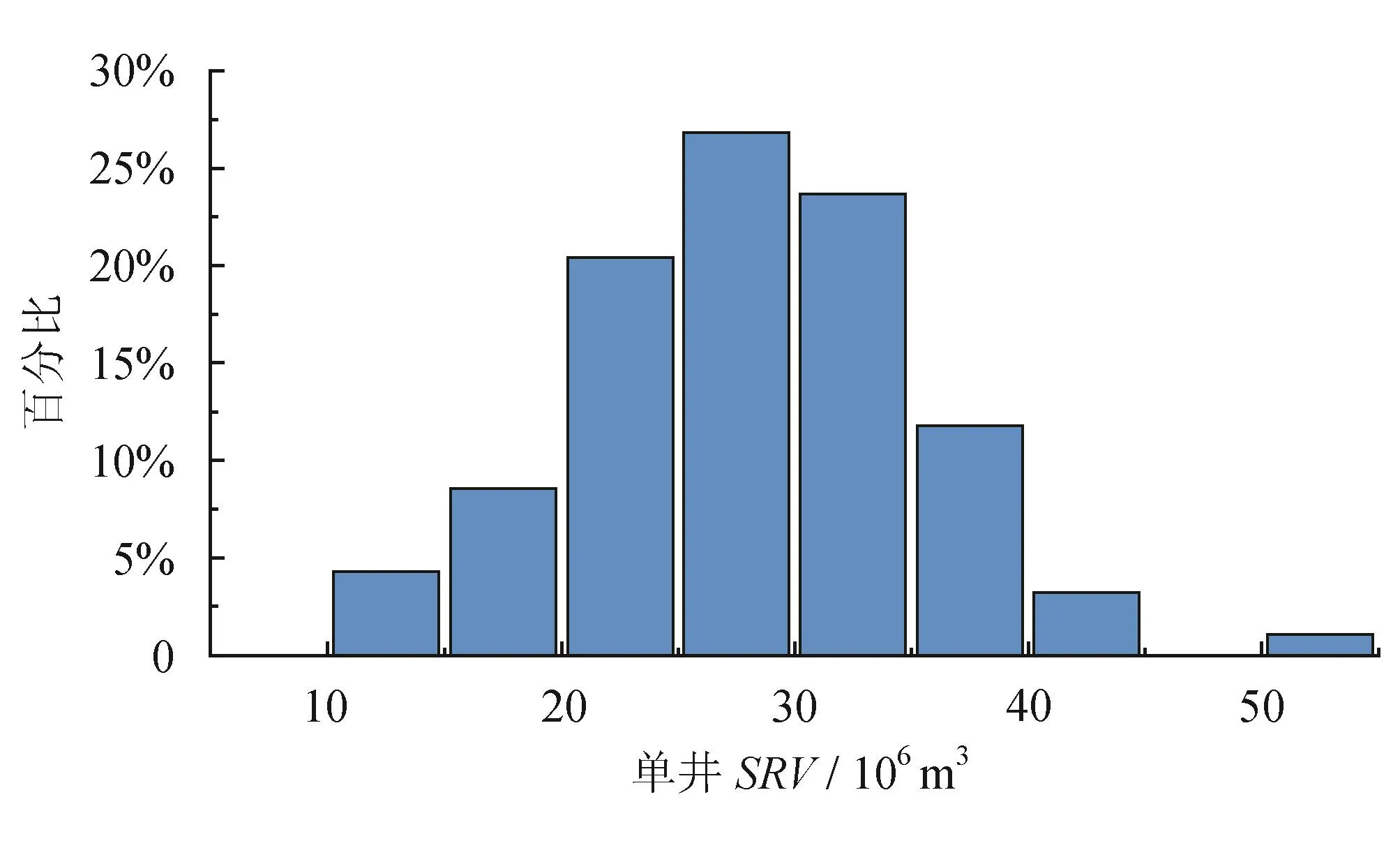
图13 FL页岩气示范区内93口压裂水平井单井SRV数据统计直方图
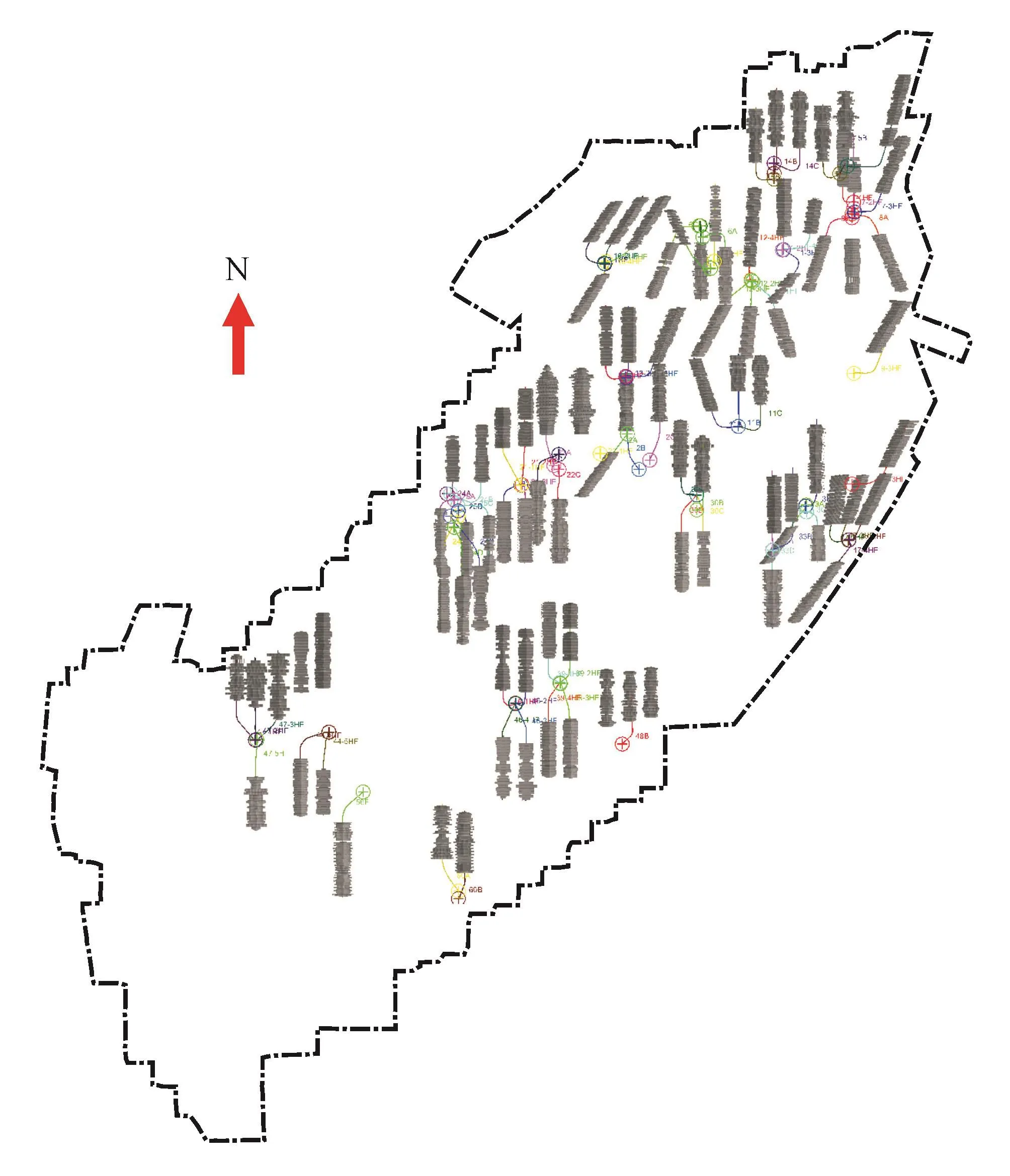
图14 FL页岩气示范区内SRV展布图
3 结论与认识
1) 基于分段分簇压裂裂缝扩展理论、岩石力学和渗流力学理论建立了页岩储层缝网压裂的SRV计算模型,该模型的计算方法与页岩压裂过程储层SRV实际物理演化过程相一致,可实现对SRV更准确地计算和定量表征。
2) 通过对模型计算结果的分析表明,模拟所得SRV与现场微地震监测结果较为符合,说明本文模型的准确性和可靠性较高,适合用于页岩气藏水平井分段分簇压裂设计与压后评价环节。
3) 模型的矿场应用表明,FL页岩气示范区内水平井分段压裂形成的SRV能够满足页岩气的高效开发,压裂增产效果明显。但部分井组间存在较大的压裂未改造区,SRV的计算表征为指导下一步加密井部署设计,提高储层总体改造程度和有效动用具有重要指导意义。

