基于不确定性用气量的输气管网供气可靠度计算方法
黄燕菲 吴长春 陈 潜 王 莉 左丽丽 赵亚南 仇 晶
1. 中国石油大学(北京) 2. 北京市燃气集团有限责任公司
0 引言
目前我国已基本形成覆盖全国大部分地区的天然气管网,同时,天然气消费量迅猛增长,预计将在2020年达到3 500×108m3。管道规模的扩大与消费量的迅速增长对天然气管道的供气可靠性提出了挑战。在天然气管道的终端用户中,居民和商业用气处于优先级最高的地位,一旦发生供气不足的情况,将优先保障二者的用气需求,而恰是这两者的用气需求呈现出较强的不确定性。因此,正确认识用气量的不确定性是保障供气可靠的关键。
在输气管网运行优化研究中,满足供气往往作为约束条件,各分输站的分输量必需满足用户用气量,尚未有将供气可靠性最大化作为目标函数的优化模型。这是由于在优化过程中,通常采用某种确定的预测结果来表示用气量,因而较容易满足供气可靠性的条件。但这种处理方法忽略了用气量变化的不确定性,会影响优化结果的客观性。因此,亟需建立涵盖用气不确定性的供气可靠性评价模型。
1 技术现状与研究进展
1.1 用气量不确定性预测
在管道运行过程中,调度人员可通过用气量预测模型预测次日、次周或次月的用气量,调整供气以满足供气需求。常见的预测模型有神经网络模型、灰色模型以及多元函数拟合法等[1-4]。其中神经网络模型能够较好地解决用气量预测中的非线性问题。
准确预测用气量是保障供气的关键[5]。但未来用气量实际是一种随机变量,采用点预测的方式无法客观体现出其随机性的特征。目前,国内尚未有表达用气量随机性的预测模型。由于管道系统和电力系统的相似性,可借鉴电力系统中负荷预测的方法。
张亚超[6]建立了基于RBF神经网络的短期负荷预测模型,并表明由于该预测结果为确定性数值,无法表达未来负荷可能的波动情况,而在电力系统中包含许多不确定性因素,从而使得决策工作面临风险。张亚超[6]通过分析历史负荷预测误差的分布特性,结合确定性的预测结果,得到一定置信水平下的区间预测结果。用其代替传统的确定性预测结果,使得决策结果更为合理。赵希人等[7]同样通过分析预测误差得到了预测结果的分布特性,并将确定性预测结果转换为概率性结果,同时给出了转化方法的数学证明。
1.2 供气可靠度
供气可靠度,即输气管网在一定时间内、一定条件下满足用户需求的概率。
大多数文献所提出的可靠性评价指标为极限状态类指标[8-15],简单地将管网状态划分成了供气可靠或供气不可靠两种状态。当某一工况下管网的供气能力大于或等于用户需求时,视为此工况下管网供气可靠;反之则管网供气不可靠。通过统计所有供气可靠工况的发生概率,得到管网处于供气可靠状态下的概率,即管网的供气可靠度。
在实际中,尤其是冬季气源供应不足的情况下,尽管用户的需求不能被完全满足,部分满足也是可以被接受的。此外,对于决策者而言,满足用户90%的需求与满足用户50%的需求,二者存在很大的差别。所以,评价供气可靠性不应该采用极限状态指标,而应该结合供气满足度指标表示。即评价结果应体现不同用户满足程度下的供气可靠度。
为此,笔者提出了一种基于用气量预测随机性的供气可靠度计算方法。该方法从用气量预测模型出发,通过分析模型的预测结果与实际用气量的误差,确定用气量所服从的分布类型及参数,从而得到用气量作为一个随机变量的表达方式。最后结合管道的最大输送能力,建立基于随机用气量的管网供气能力优化模型和供气可靠度计算方法。
2 模型建立
2.1 用气量预测模型
笔者采用了基于小波分解的神经网络模型预测某天然气长输管道的日供气量。样本从2015年1月2日—2016年12月31日每日的用气量和日期类型、天气参数,用气地点为英国某郡。样本个数共计727个,其中85%(618个样本)用作训练预测模型,15%(109个样本)用于测试模型准确性。
2.1.1 数据预处理
标准化也名为归一化,是将不同数量级的数据转变为同一数量级的方法。不同类型的影响变量往往具有不同的量纲和量纲单位,会影响模型拟合结果。为了消除不同类型变量之间的数量级的差异,需要进行标准化处理,以解决变量之间的可比性。
笔者采用了最大—最小标准法,对于每一种变量X中的每一个变量x进行如下变换,使得所有输入变量x的范围都在[-1, 1]区间:
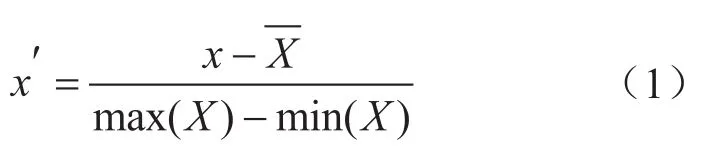
式中x表示原变量;x'表示x变换后的变量;X表示X类型变量的均值;max(X)表示X类型变量中的最大值;min(X)表示X类型变量中的最小值。
当用气量包含了居民用气时,其随时间的变化曲线往往呈现不确定性的扰动,为了使预测模型更好地预测出用气量,可以对历史用气量曲线做小波分解,分离出高频的扰动和低频的较为稳定的用气量(图1),再将高频和低频信息作为数据输入至预测模型中。
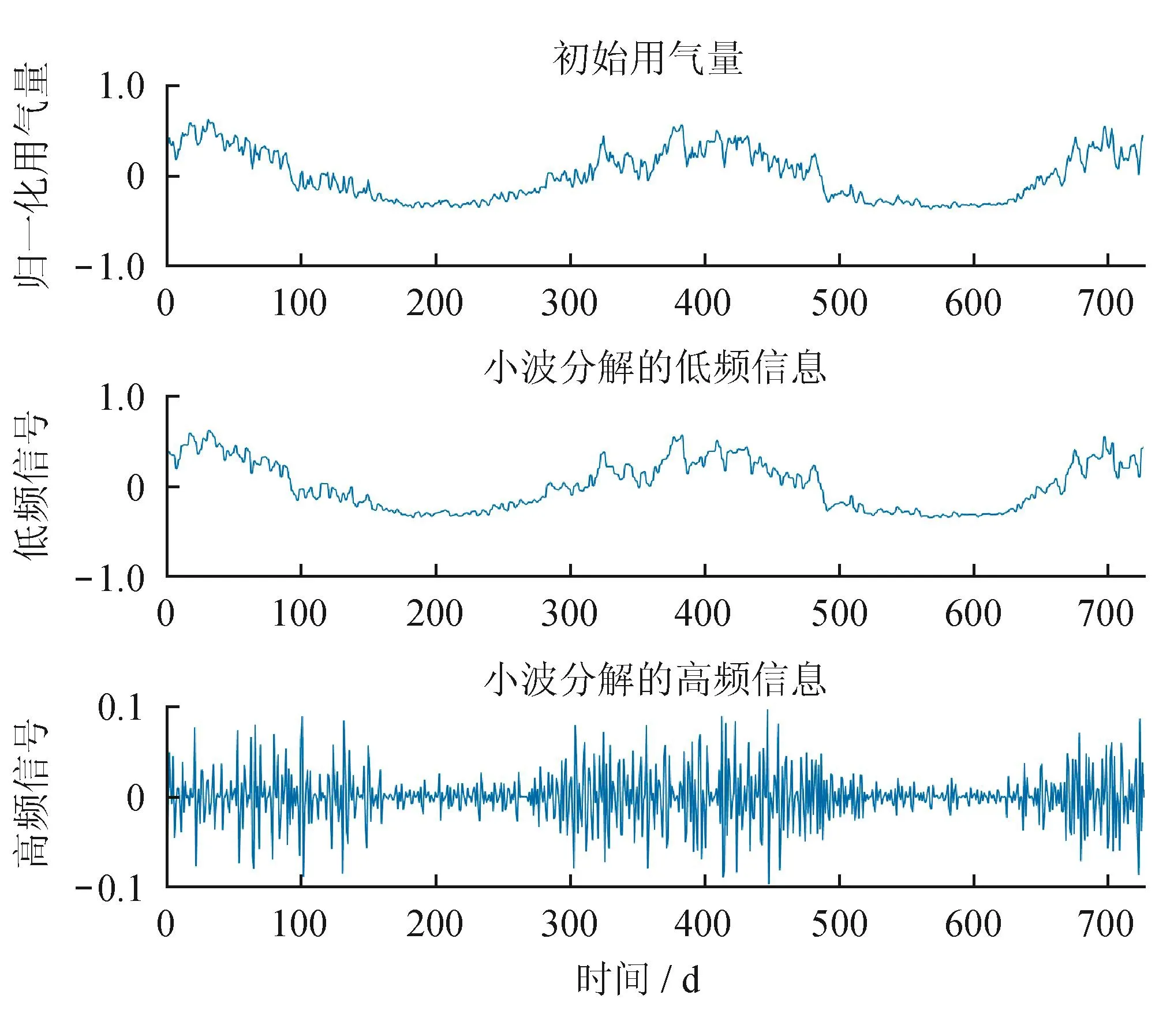
图1 小波分解的用气量曲线图
2.1.2 神经网络结构
神经网络模型的每一层输入数据都经过如下变换:
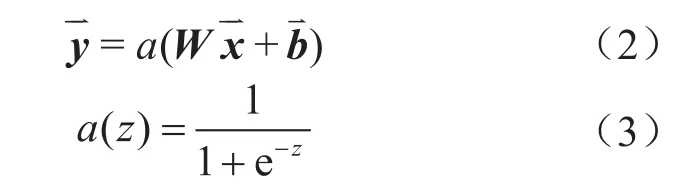
模型的损失函数为均方差MSE函数,即
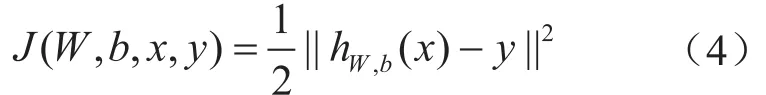
模型所输入数据包括预测日的日期类型:星期、月份和年份;预测天气参数:温度—风力指数;历史用气量:前一天的实际、高频、低频用气量和前3天的实际、高频、低频平均用气量。输入共26个维度的变量;输出数据则是预测日的用气量。
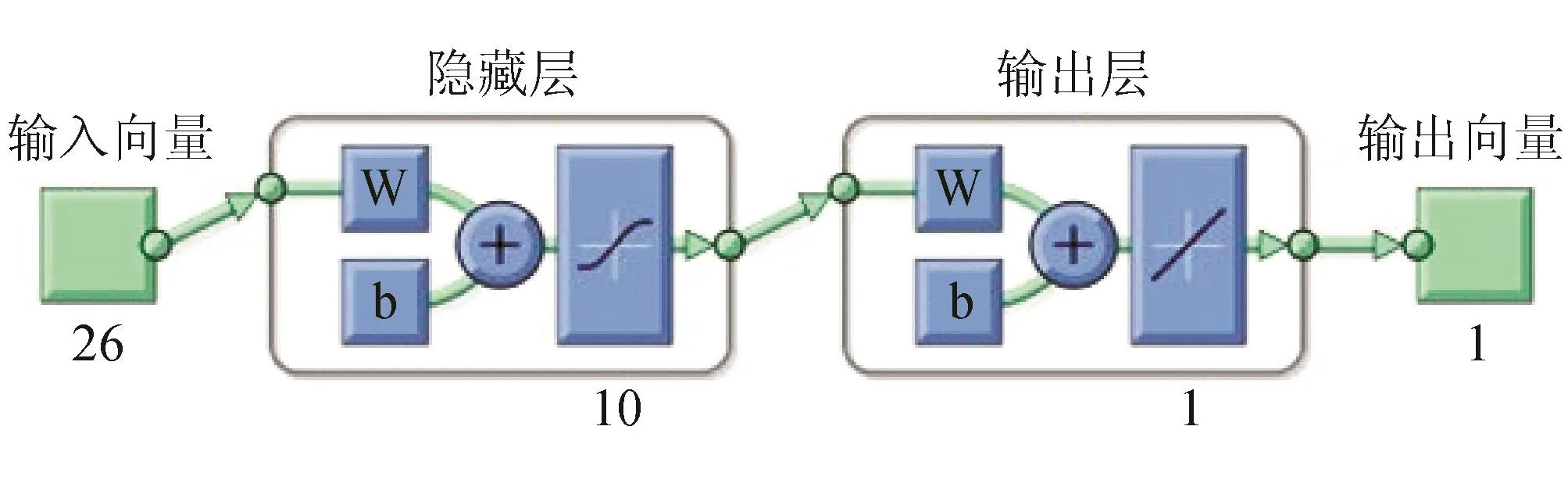
图2 神经网络模型结构图
2.1.3 预测模型结果
经过验证,模型具有较好的准确性,预测用气量与实际用气量比较如图3所示,预测结果相对误差的绝对值平均为3.2%。
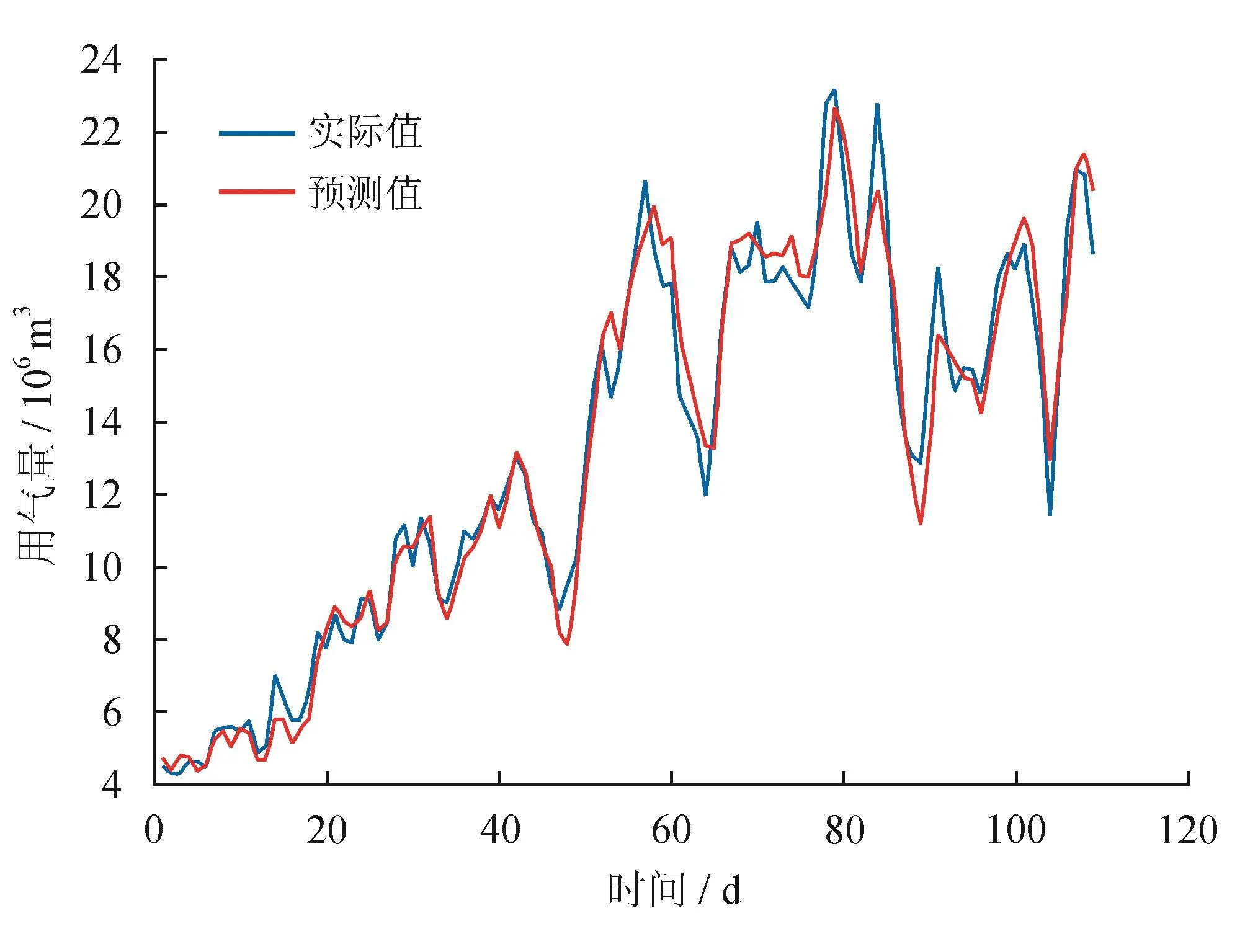
图3 用气量预测模型结果与实际值对比图
2.2 用气量不确定性变化
通过分析相对误差的分布,可将模型预测的用气量转变为服从正态分布的随机变量。预测用气量的相对误差为:
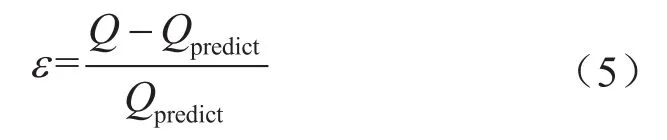
式中ε表示预测值的相对误差,Q表示预测日的实际用气量;Qpredict表示预测日的预测用气量。
从图4可以看出,预测误差基本服从正态分布,对误差样本进行正态拟合,得到相对误差的均值(με)为-0.003 2,标准差(σε)为0.066 8。
经柯尔莫哥洛夫—斯米尔诺夫(K—S)检验,在显著性水平为0.05时,误差服从正态分布,即ε~N(-0.003 2, 0.066 82)。
实际上,对于较好的预测模型,其相对误差都应当服从均值近似为零的正态分布。这是因为较准确的预测模型其误差主要来自于偶然误差,而偶然误差是服从正态分布的;反之则说明系统误差占主导,此时应重新检验模型。
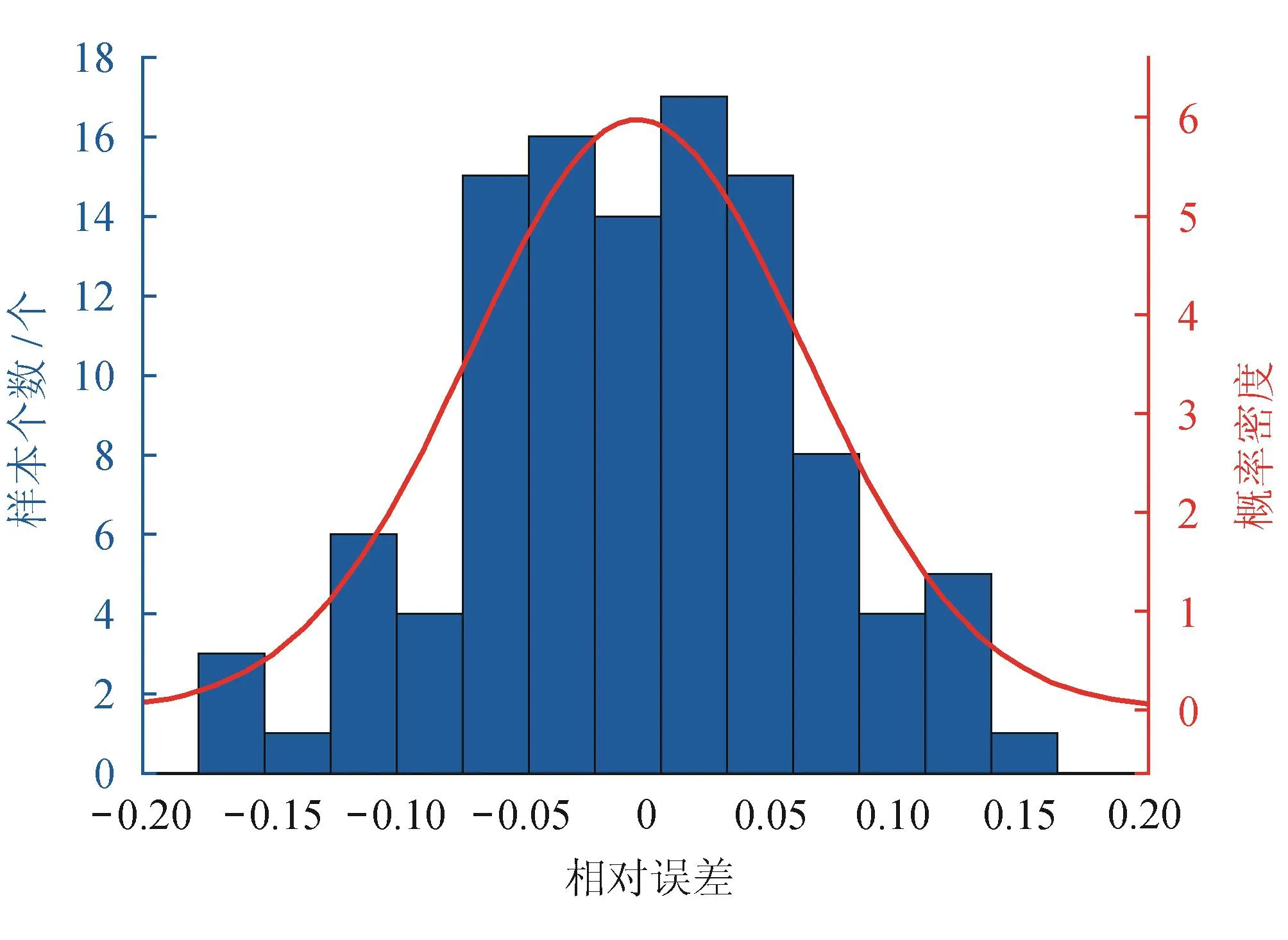
图4 误差直方图及其拟合的概率密度曲线图
由公式(5)可知,实际用气量可以由预测用气量和预测相对误差表示,即

由高斯分布的性质可通过公式(7)计算用气量所服从正态分布的均值(μQ)和标准差(σQ),即
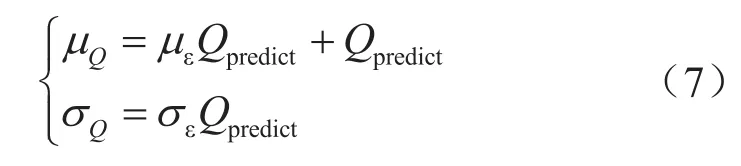
由此,即可得到预测用气量的随机性表达:
(8)式中μQ表示用气量服从正态分布的均值;σQ表示用气量服从正态分布的标准差;φ(Q)表示用气量为Q时的概率。
图5表示了某一星期的用气量预测曲线,以及在星期四该日用气量的概率密度分布曲线(图5中的小图)。
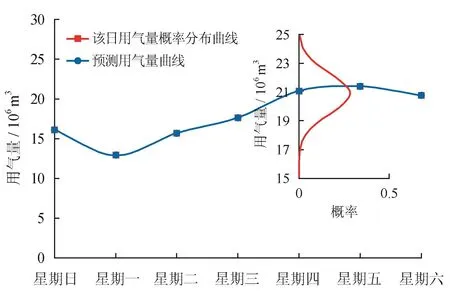
图5 预测用气量及其概率分布图
则用气量概率的累计分布见公式(9)及图6。
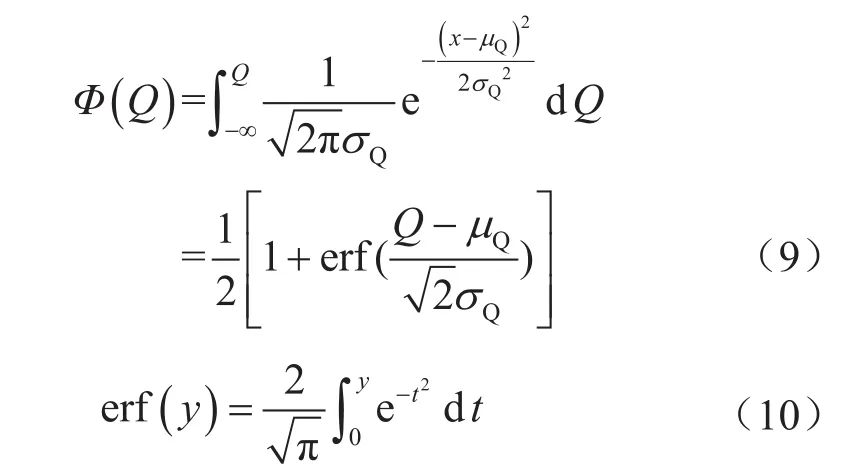
式中表示用气量的累计分布函数,即用气量小于或等于Q的概率;erf(y)表示误差函数,形状亦与图6类似,该函数没有解析解。
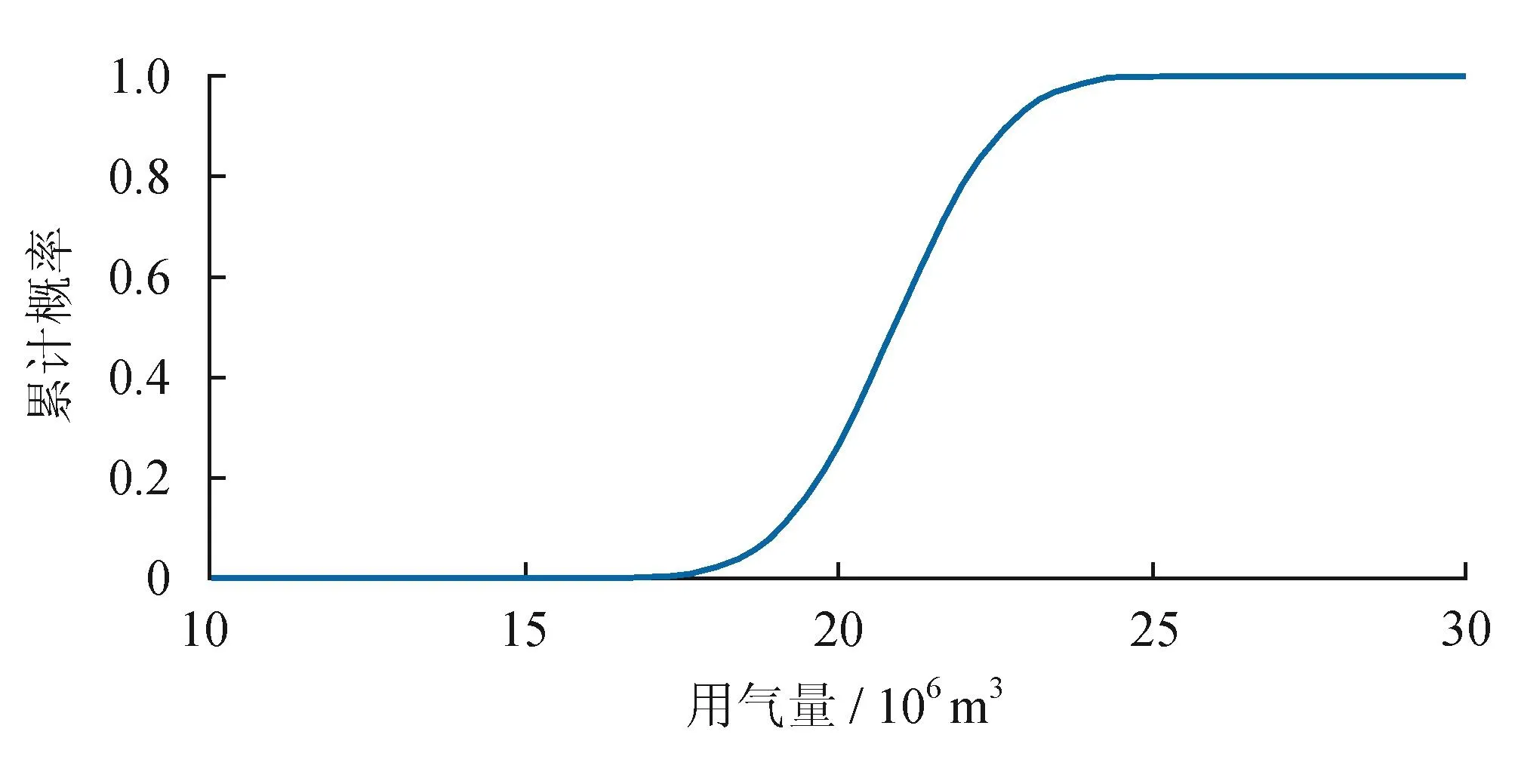
图6 用气量概率累计分布曲线图
当面临着供不应求的情况时,决策者往往更关注管网在不同用气需求满足程度下的可靠度。由正态分布的性质可求出用气量在不同用气满足程度时的概率分布:
例如,若某用户的用气量Q服从均值为μQ、标准差为σQ的正态分布那么该用户80%的用气量0.8Q则服从均值为0.8μQ、标准差为0.8σQ的正态分布
则当用气量Q≤管网的供气能力Qsupply时,可称为满足用气量需求,此事件发生的概率为P(Q≤类似地,当管网的供气能力Qsupply>80%的用气量时,可称为满足80%用气量需求,此事件发生的概率为
其中,Φ80%表示80%的用气量的累计分布函数,即
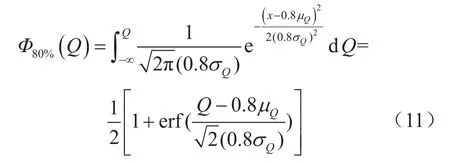
需要注意,笔者所提出的用气量随机性转化方法并不局限于神经网络预测模型。对于所有类型的用气量预测模型,当其预测样本达到具有统计意义的数量时均可采用此方法。
2.3 流量分配模型
已知用气量的分布函数后,再计算出管网的供气能力,即可通过公式(9)得到管网的供气可靠度。管网的供气能力是指管网在给定工况下所能够向用户输送的最大气量。管网的实际供气能力与各管道的压力、流量和管存等参数有关。在实际运行中这些参数会随着时间不断变化,若采用水力—热力模拟的方法获得这些参数,计算量是巨大的。因此,在最大流算法的基础上[16-17],提出一种基于管道最大输量和用气量不确定性的稳态供气可靠度计算方法。将管网的拓扑结构用有向图表示,通过水力计算得到每段管道所能允许通过的最大流量,在此约束下求出使各个用户用气量满足概率最大(即可靠度最高)下的流量分配,从而得到管网的最大供气能力。在考虑了社会影响和政策等因素后,对不同用户进行分级,各个用户重要程度通过加权体现。对于居民用气等必须满足的用户,可设定较高的权重优先保障;反之,对于工业用气等可中断用户可设定较低的权重。
此外,假设上游气源不存在相对短缺的情况。当气源短缺时,通过简单计算即可得到各用户的用气满足程度,在此不做赘述。
2.3.1 决策变量
决策变量分为两种,分别是每段管道中的流量(F)和向各个用户的供气量(Q)。当流量和供气量确定后,即可知道管网的流量分配和总供气量,从而可通过公式(9)得到针对各个用户和管网总体的供气可靠度。
2.3.2 目标函数
为使得管网供气可靠度最大,目标函数为最大化各个用户用气量满足概率的加权之和,即
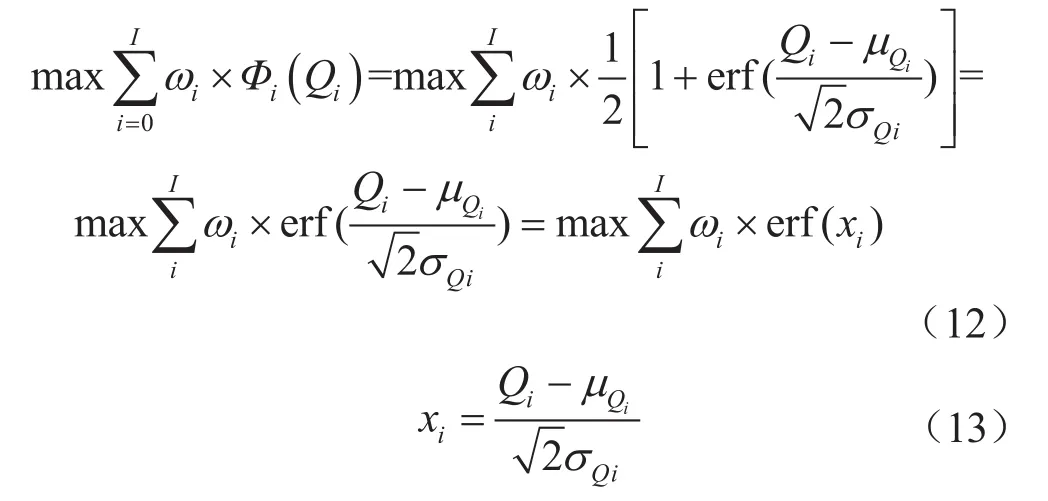
式中i表示用户编号;I表示所有用户的集合;wi表示第i个用户的权重,Qi表示对第i个用户的供气量;xi表示对第i个用户的供气量的线性变换。
2.3.3 约束条件
1)用户分输流量的约束:
每个用户i的分输流量必需大于等于0,即

2)管道中流量的约束:
对于从节点a到b之间的管道,其中的流量必需大于等于零(正向流动)且小于等于管道的允许最大流量,即
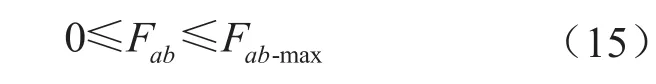
3)节点的流量平衡约束:
对于每个节点b(压气站V,不包括分输点I),流入的流量之和必须与流出的流量之和相等,即
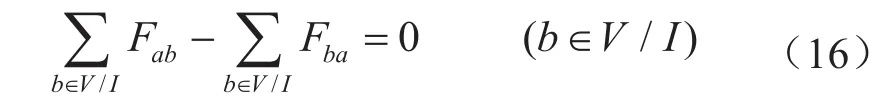
2.4 修正模型
从公式(9)可看出,管道供气量越大,满足用气量的概率越接近于1;反之,当满足用气量的概率为1时,管道的供气量将接近于无穷大,这是明显无法满足的。可以对每个用户i的分输流量取上限μQi+3σQi,即不满足的概率在2‰以下是可以接受的。若对可靠性有更高要求,上限可取更高值。
一般管网的最大输量都可基本满足用户需求。为了避免优化模型盲目地追求权重高的分输点流量最大,当管网的允许最大输量大于各分输点用气量均值之和时,可提高用户i流量约束的下限为μQi。
由此,分输点流量约束为:
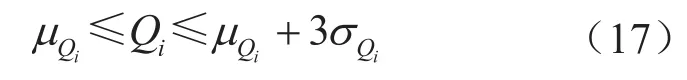
此外,在原模型中,目标函数是非线性的,若采用遗传算法等启发式算法求解,不仅不能保证获得全局最优解,而且计算量较大。
由于公式10是单调递增的。故在管网设计输量能大致满足用户需求的情况下,可线性化目标函数,提高计算效率,此时最优解为原问题的一个局部最优解。
改进的优化模型见公式(18)。I、V分别为用户、节点(分输点和压气站)集合。
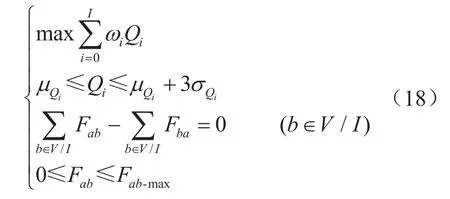
3 算例分析
3.1 管网数据
笔者对一虚拟管网进行可靠性评价,管网拓扑结构见图7,其中A、B、C、D、E、F、G是节点;PIPE为管道;INPUT为气源;OUTPUT为用户。其余参数如表1所示。
取用气量上限为μQi+3σQi,即满足此上限时可靠度为99.865%,可视作达标。用户的用气需求见表2。
3.2 可靠度计算
通过最大流算法可得出,在不考虑各个分输点用气分配的情况下,该管网的最大供气能力为1 073 m3/s,大于各分输点用气量预测均值之和1 000 m3/s。通过修正模型[公式(17)]计算结果见表3,最优值即管网总体可靠度为95.270%。可看到除了用户OUTPUT4外,其余用户可靠度均达到要求(99.865%)。导致供应用户OUTPUT4的流量未满足的原因有2点:①管道的允许输送能力限制;②该点的权重系数较小。
进一步提高可靠度达标线为99.999%,结果见表4,管网总体可靠度为88.110%。此时只有2、3、5号用户能够达到99.999%的用气需求,其中3和5号是权重较大(优先级较高)的用户。在满足了3和5号用户后,由于2号用户距离气源较近,且其需求量较小。因此也被优先满足。
由于管网状态并未改变,管网总体可靠度降低,可见这3个用户可靠度的提高,是以牺牲其他用户可靠度为代价的。
在可靠度达标限制为99.999%的基础上使各用户的权重相等,即没有优先满足某些用户的要求。计算结果见表5,管网可靠度为89.730%,相比上一算例提高了1.84%。此时,优化模型会优先满足距离气源点最近的用户,即1、2、3号,此时气体输送成本较低。
在可靠度达标线为99.999%,1~5号用户权重分别为1/6、1/6、1/4、1/6、1/4的条件下,各用户和管网在不同用户满足度条件下的可靠度曲线见图8。
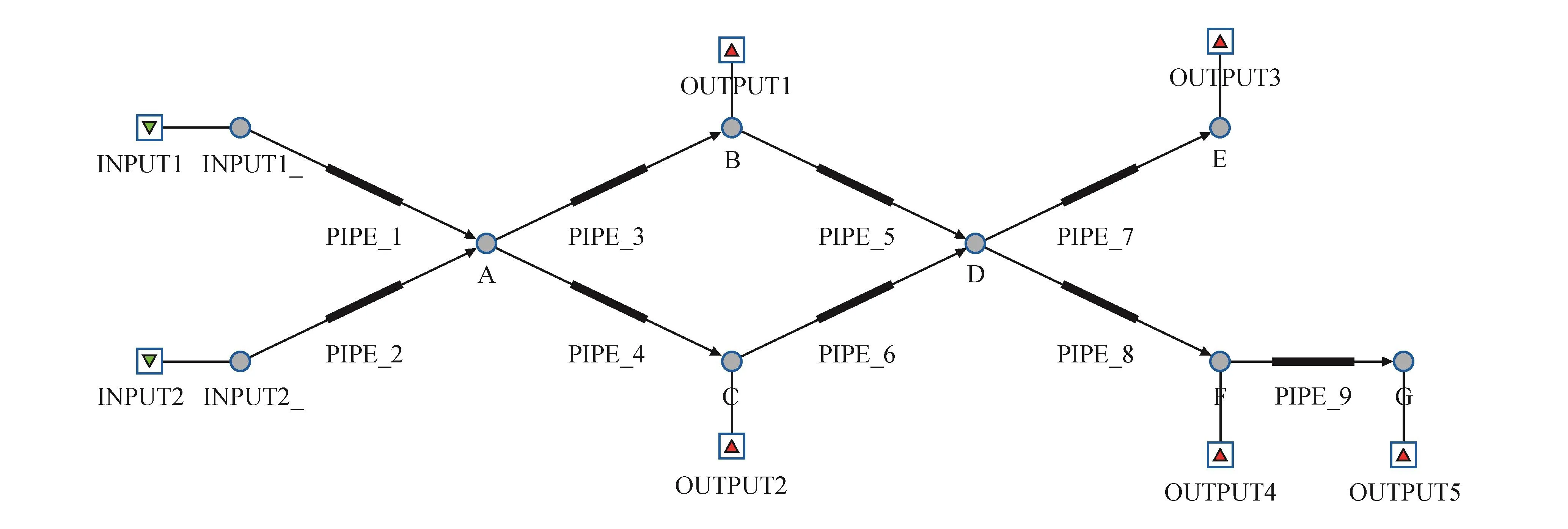
图7 管网拓扑结构图

表1 各管道最大允许输量表

表2 用户用气量随机性表达表
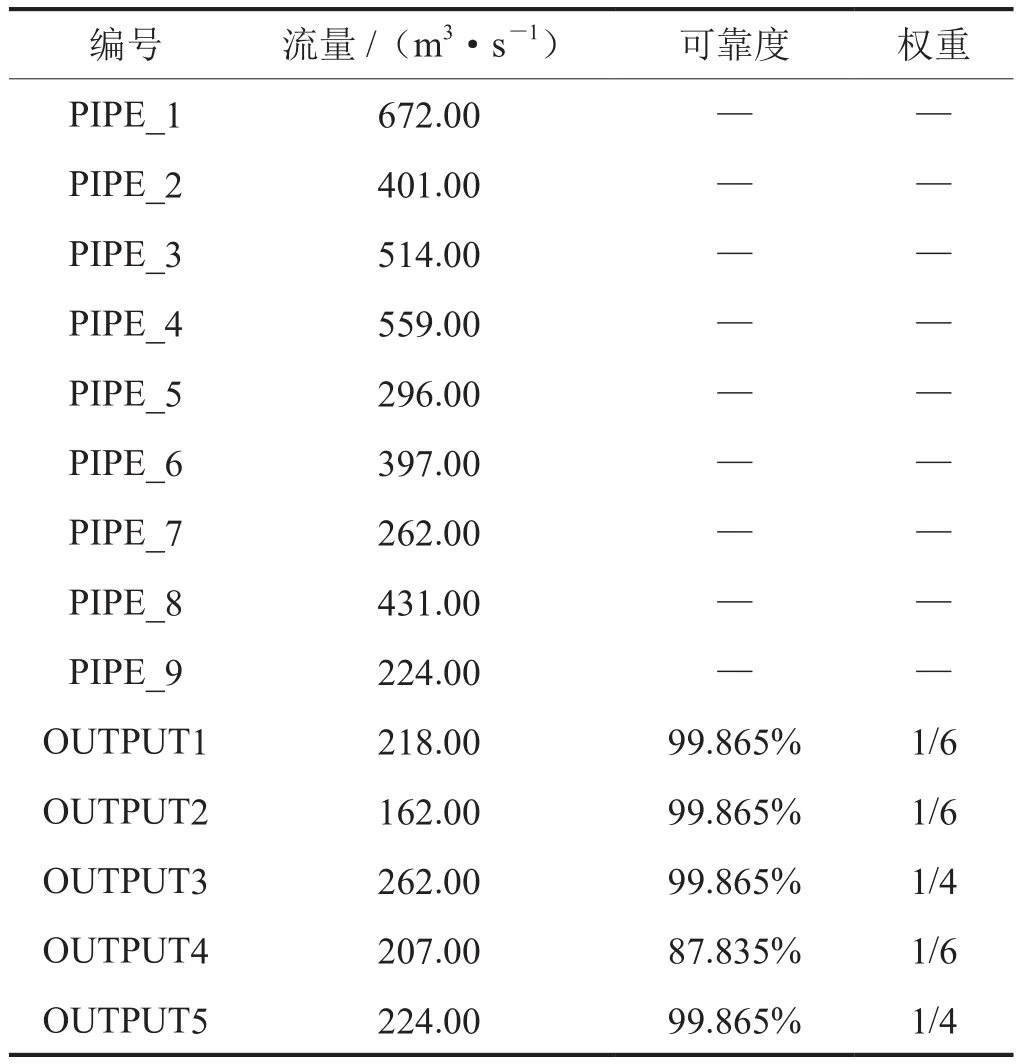
表3 各管道/分输流量表
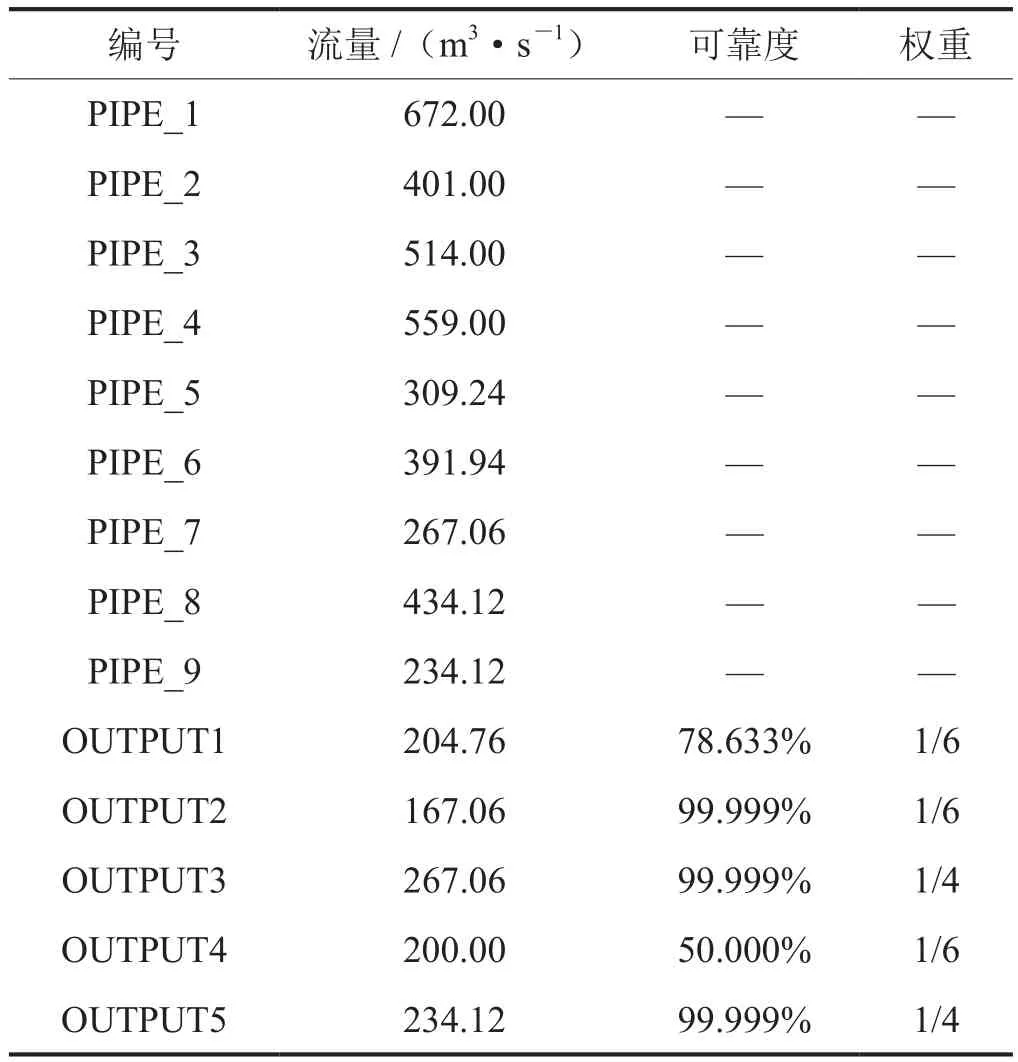
表4 提高可靠度标准后各管道/分输流量表
其中,由于3号和5号用户权重较高,二者可靠度相同(可靠度曲线重合),在不同满足度条件下始终为99.999%。而随着对用户满足度要求的降低,1、2、4号用户的可靠度也可达到99.999%。
4 结论
1)提出了一种基于用气量不确定性的可靠性评价方法。该方法从用气量预测模型出发,通过分析预测误差得到预测用气量的概率表达。在分析管网拓扑结构的基础上,通过水力计算得到管道的允许最大输气量,从而建立以总体供气可靠度最高为目标的管网流量分配优化模型,求解得到管网的最大供气能力及管网和各个用户的供气可靠度。
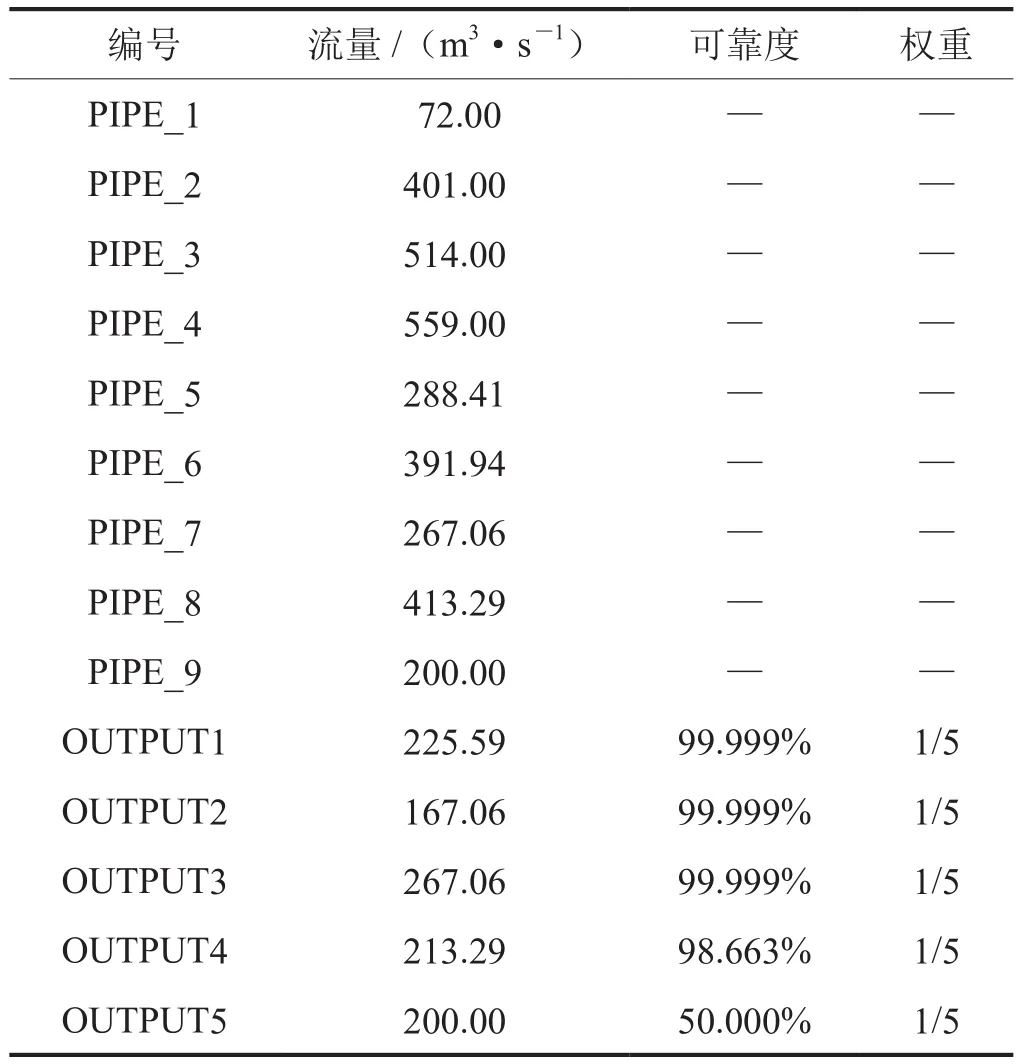
表5 无加权下各管道/分输流量表
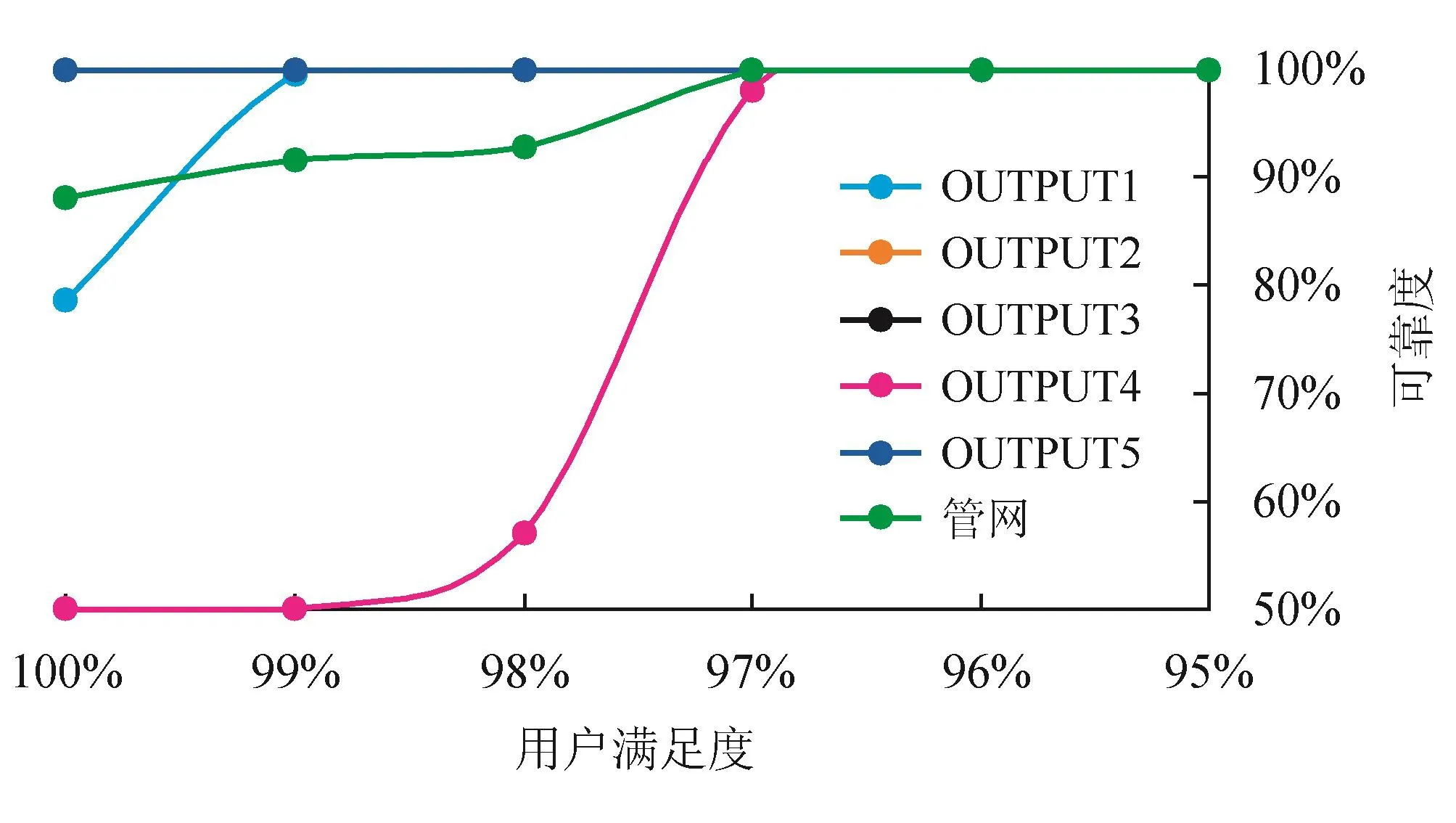
图8 不同用户满足度下各分输点和管网的供气可靠度曲线图
2)通过算例分析,模型求解的流量分配方案优先保障权重较大/较为重要的用户,但会牺牲其他用户的供气可靠度,管网总体供气可靠度亦会下降;在取消权重后,管网总体供气可靠度提高,优先保障距离气源地较近的用户。若不要求完全满足用户的用气量,则在降低一定标准后,所有用户的可靠度都会达标。
3)所提出的可靠度计算方法结合了用气量随机的特性,能够更加客观地评价管网的供气可靠度。同时引入了用户的权重,在计算管网供气能力时候能够优先满足重要的用户,更加符合实际情况。评价结果可以有效地指导管网的安全运行。

