基于主基底分析降维方法的水稻冠层叶片叶绿素含量估算

袁炜楠，许童羽,2*，曹英丽,2，王洋，于丰华,2

（1.沈阳农业大学信息与电气工程学院，沈阳110161；2.辽宁省农业信息化工程技术中心，沈阳110866）

植物通过光合作用进行物质和能量交换，叶片中的叶绿素作为光合作用的主要色素，是光合作用能力、叶片氮含量和作物发育阶段的指示物，因此，获取叶绿素的变化信息已成为检测作物长势的重要手段[1]。然而，传统的化学分析方法具有破坏性，且耗费人力，时间长，成本高。高光谱遥感技术是一种便捷、低成本的监测手段，它使窄波段光谱信息的获取成为可能。近年来发展了一系列窄波段组合运用于叶片色素含量的估算[2]，为作物叶绿素含量的定量诊断提供了简便有效、非破坏性的数据采集和处理方法[3]。

利用高光谱技术估算叶片中的色素含量主要有2类方法模型：物理模型[4]和经验模型[5]。近年来，国内外学者在利用高光谱遥感数据监测植被叶绿素含量方面做了大量的研究。HUNT等[6]和李粉玲等[7]利用高光谱特征波段组合构建了估算作物冠层叶绿素含量的遥感模型；李媛媛等[8]利用叶片高光谱特征波段组合构建了估算作物叶片叶绿素含量的遥感模型；丁永军等[9]通过把原始光谱数据进行一阶微分和去除包络线等处理后，结合波段自相关分析建立了多元线性回归模型，并对番茄叶绿素含量进行反演；岳学军等[10]在主成分分析降维的基础上利用支持向量机回归算法和偏最小二乘回归模型预测了柑橘叶片叶绿素含量；邓小蕾等[11]应用波段间相关系数分布对光谱数据进行降维，建立了苹果叶片叶绿素含量的逐步回归模型。周冬琴等[12]选出了与水稻氮含量相关性较好的5个波段，建立回归方程对氮素进行反演。CHEN等[13]利用绿峰、红边位置、高光谱特征波段组合作为反向传播（BP）神经网络的输入变量对水稻叶绿素含量进行了估算，并与线性回归模型进行比较分析。目前，降维方法有主成分分析、因素分析、典型相关性分析，以及偏最小二乘回归、分段逆回归等，这些方法的共同特点是依照某种最优化原则，在原变量X1，X2，…，Xp中提取成分F1，F2，…，Fm（m＜p），再利用这些成分进行相关的分析工作。但是，由于每一个成分都是原始变量的线性组合，所以这些方法都没有筛选变量的功能[14]。还有一些学者只选取几个波段建立植被指数进行降维，但这种方法只选择了波段中的很小一部分，造成数据的大量舍弃，而且对原数据进行了数学变形，丢失了原数据的信息。

本研究提出了一种基于主基底分析的降维方法，通过对降维后的光谱与对应的叶绿素数据建立回归模型来进行叶绿素含量的估算。本文选取对叶绿素敏感的400～1 000 nm[15]波段进行Gram_Schmidt变换并找到投影空间，构造集中波段信息的主基底来进行建模，并与选取的植被指数降维法进行对比分析，以期为光谱数据降维估算叶绿素含量提供一种行之有效的方法。

1 材料与方法

1.1 试验设计与样品采集

试验于2017年6—9月在辽宁省沈阳市沈阳农业大学辽中区卡力玛村院士工作站进行。供试水稻品种为千重浪1号，试验时间包含了水稻生长的分蘖期、拔节孕穗期、抽穗灌浆期和成熟期。工作站近几年种植作物均为水稻。试验田中共设4个施肥梯度，分别为无氮（N0）、低氮（N1）、正常氮（N2）和高氮（N3）；小区面积6 500 m2，每个水平3次重复，共12个小区，随机分布，如图1所示。每星期无人机飞行采集1次，共进行13次试验。每次从每个小区选取3穴具有代表性的水稻作为样本，每穴水稻随机采集2片叶，装入密封袋中并标注小区的名称及编号，采集后立即运回实验室。从得到的936组样本中随机抽取736组作为建模样本，剩余200组作为检验样本。

1.2 冠层光谱数据采集与叶绿素含量测定

图1 水稻小区分布图Fig.1 Distribution map of riceplot

图2 无人机平台Fig.2 Unmanned aerial vehicle(UAV)platform

本试验采用飞行高度50 m的中国GaiaSkymini无人机高光谱成像系统进行水稻冠层光谱反射率的采集，如图2所示。为了获取稳定的水稻冠层高光谱反射率数据，选择天气晴朗、少风或微风的天气，在10：00—14：00之间飞行采集；该光谱仪的光谱范围为400～1 000 nm，输出间隔为1 nm。从各次试验的高光谱图像中，每个小区随机选取6个点作为样本点，每个样本点采集1条光谱曲线。

叶片的叶绿素含量采用分光光度计进行测定。叶片用蒸馏水洗净后吹干，去掉中脉后剪碎，混匀；称取剪碎的新鲜叶片0.2 g，放入研钵中，加入少量石英砂和碳酸钙粉及2～3 mL 80%丙酮，研成匀浆；再加入10 mL丙酮，继续研磨至组织变白，静置3～5 min。在漏斗中放置滤纸，用丙酮润湿，经过滤和反复冲洗研钵和研钵棒以确保叶片色素全部进入25 mL棕色容量瓶中；用吸管吸取丙酮，将滤纸上的叶绿素也冲洗至容量瓶中，直至滤纸上无绿色为止；最后用丙酮定容至25 mL，摇匀，于避光处静置2 h。取萃取液装入光径1 cm的比色杯内，以80%丙酮为空白对照，测定在波长为649、665 nm处的吸光度，利用式（1）、（2）和（3）计算叶片中叶绿素的质量浓度。

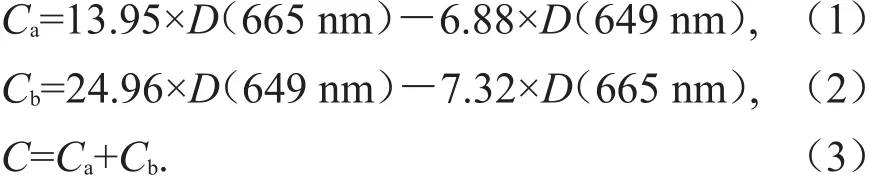
式中：D（665 nm），D（649 nm）分别为在665 nm与649 nm波长下的吸光度；Ca，Cb分别为叶绿素a与叶绿素b的质量浓度，mg/L；C为总叶绿素的质量浓度，mg/L。

1.3 Gram_Schmidt变换原理

任意一组线性无关的变量X1，X2，…，Xs，总可以经过Gram_Schmidt变换把它们变换成正交变量Z1，Z2，…，Zs，Gram_Schmidt变换公式见式（4）。

JAIN等[16]对式（4）进行了详细证明，且通过Gram_Schmidt变换可以得到如下推论：对于任意一组 秩为 s(s≤p)的变 量 X1，X2，…，Xp，对 它 们 做Gram_Schmidt变换后，得到 Z1，Z2，…，Zp；这其中必有Z1，Z2，…，Zs是相互直交的，且Zs+1=…=Zp=0。从推论可以看出，Gram_Schmidt变换有2个功能：1）将变量集合中的信息进行正交分解；2）排除X1，X2，…，Xp中的冗余变量（即被变换成0的那些变量）。

1.4 高光谱降维方法

影响叶绿素的光谱波段范围为400～1 000 nm，各波段间存在一定的相关性，如果不做降维处理，在对光谱数据进行叶绿素反演时，需要的数据量将呈指数幂增加，给数据处理带来困难。因此，本研究采用基于主基底分析的降维方法，其原理是通过Gram_Schmidt变换找到波段的投影空间，在投影空间下构造出最大限度涵盖原始变量信息的低维变量，该低维变量即为波段的主基底，利用建立的主基底变量代替原来的光谱波段数据。

投影空间的构造原理如下：设研究的每组对象涉及p个变量，共有n组对象，则构成一个n×p的数据矩阵，X=[x1x2…xP]。

1）选择与健康水稻叶片最接近的一列数据xm作为h1，计算其内积hT1h1，将其值作为初始能量，则

2）将xm从矩阵XT中去除，选择剩余数据的第一列，与z1作Gram_Schmidt变换，得到h2，计算其内积，则将h2作为投影空间的第二，则选择剩余数据的下一列。

3）选择zm列时，与z1，z2，…，zm－1进行Gram_Schmidt变换得到hm，计算其内积hTmhm；如果则将hm作为投影空间的第m列zm。

4）重复以上过程，直至经Gram_Schmidt变换后得到n个相互正交的向量z1，z2，…，zn，即为投影空间。

将光谱数据与投影空间相乘，得到所求的波段主基底；具体的技术流程如图3所示。

图3 技术流程图Fig.3 Techniqueflow chart

2 结果与分析

2.1 不同施氮量条件下水稻叶片高光谱特征

图4是千重浪1号水稻在不同施氮量下的光谱特征曲线。从中可知，在不同氮素水平下，水稻光谱反射率的变化明显，说明可以进行叶绿素的反演。

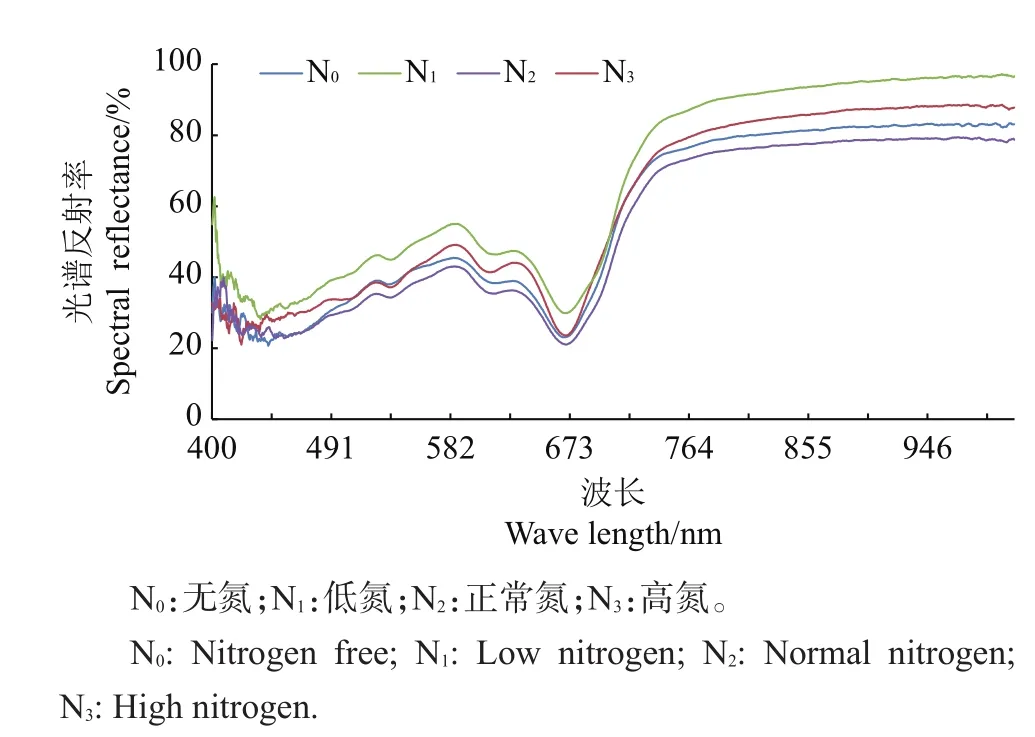
图4 不同氮素水平下水稻叶片高光谱曲线Fig.4 Hyperspectral curves of rice leaves under different nitrogen levels

2.2 不同叶绿素含量的水稻叶片高光谱特征

如图5所示：不同叶绿素含量的水稻叶片高光谱特征总体上保持一致，在400～500 nm的蓝紫光波段和650～700 nm的红光波段处形成2个吸收谷，在500～600 nm波段处形成1个反射峰，在650～750 nm的近红外波段处光谱反射率开始急剧上升，在750 nm波段处达到最大反射率值并趋于平稳；同时，不同叶绿素含量会造成光谱反射率曲线的变换，即光谱曲线会随着叶绿素含量的增大向下移动。由此可以看出，水稻叶片光谱曲线特征与叶绿素含量有着密不可分的关系。因此，可以将光谱反射率与叶绿素含量建立相关性来估算叶绿素的含量。

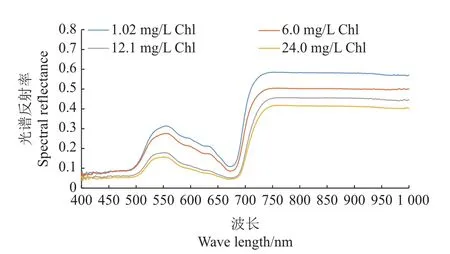
图5 不同叶绿素含量的水稻叶片高光谱曲线Fig.5 Hyperspectral curves of rice leaves with different chlorophyll(Chl)contents

2.3 基于主基底分析降维与模型的估算

选取736组光谱数据进行主基底分析降维。在主基底分析的基础上，建立波段长度为5、10、15、20、25、30、35和40 nm的窗口，对波段进行分组并找到主基底，建立主基底与叶绿素的线性函数、二次函数、指数、对数、幂函数、最小二乘回归模型，依据决定系数（R2）、均方根误差（root mean square error,RMSE）与主基底维数3项指标，选出窗口大小正好和精度最高的回归模型。在模型精度上，最小二乘回归模型精度明显高于其他回归模型，基于最小二乘回归模型的窗口指标情况如表1所示。从中可以看出：随着窗口大小的增加，R2逐渐减小；从窗口大小为30 nm开始，R2维持在0.68左右，RMSE达到最小值，主基底在48维处趋于稳定。因此，选择分段长度为30 nm的窗口最佳。

表1 波段窗口指标Table1 Band window indicator

对736组400～1 000 nm波段的光谱数据以30 nm窗口分段，分成20段，应用MATLAB R2016a编程，逐次选择每段进行Gram_Schmidt变换，共找到48列数据组成的投影空间。将每段光谱数据与对应的主基底相乘，得到光谱数据的主基底。736组400～1 000 nm波段的光谱数据主基底构成736×48的数据矩阵，光谱数据从601维降到48维。

应用最小二乘回归法建立叶绿素估算模型，Y=BX+A。其中：Y为叶绿素值；X为波段主基底；B为48个数据组成的数组；A为常量。因此，该模型需要48个输入变量，主基底中的48列数据即为输入变量。应用剩余的200组光谱数据进行验证，把波段进行30窗口的分段，每段光谱组成的200×30数据矩阵与各组投影空间相乘，得到测试数据200×48矩阵的主基底，每行作为最小二乘回归模型的输入，得到200组预测叶绿素值，并与200组真实叶绿素值进行比较，结果如图6所示。从中可以看出，叶绿素实测值与预测值的RMSE为1.20。

2.4 植被指数与水稻叶绿素的相关性

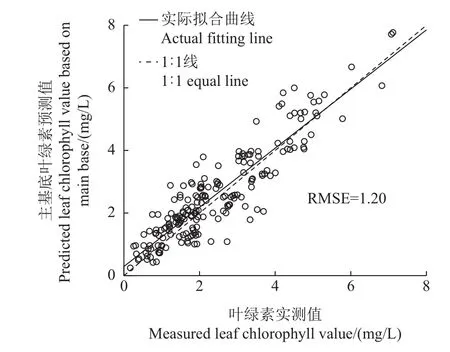
图6 叶绿素实测值与预测值比较Fig.6 Comparison of measured and predicted leaf chlorophyll values

依据表2中的公式计算植被指数，分析植被指数与叶绿素的相关性。从中可以看出：3种植被指数与叶绿素值均达到极显著相关水平（P＜0.01），光化学反射指数（photochemical reflectance index,PRI）与叶绿素值呈正相关，即叶绿素值随着植被指数的增加而增加；差值光谱指数（RD2）、叶绿素吸收比指数（modified chlorophyll absorption ratio index,MCARI）与叶绿素值呈负相关，即叶绿素值随着植被指数的增加而降低。其中：PRI与叶绿素值相关性最高，达到0.682；MCARI与叶绿素值的相关性最低，为－0.605。根据统计学分析，以上3种植被指数与叶绿素值均达到中度相关，说明这些植被指数能够很好地反映叶绿素值的变化，能够用来搭建估算模型。

表2 常用光谱指数Table 2 Common spectral index

2.5 基于植被指数降维的叶绿素估算模型及其检验

根据植被指数构建的线性函数、二次函数、指数、对数、幂函数、最小二乘回归模型精度的不同，以决定系数（R2）、均方根误差（RMSE）和相对误差（relative error,RE）为指标，选择出所选植被指数拟合度较高的回归模型作为估算模型，结果如图7所示。拟合方程中x为PRI值，y为实测的叶绿素值。基于3种植被指数PRI、RD2和MCARI建立的回归模型均能较好地估算叶绿素值，其中：R2分别为0.538、0.468和0.452，RMSE分别为3.295、3.761和3.872，RE为4.608%、5.407%和5.504%。基于植被指数PRI所建立的指数模型精度最高，拟合方程为y=3.825e14.707x。图8为200组检测数据对估算模型的验证。可以看出，3种植被指数PRI、RD2和MCARI估算模型的RMSE分别为3.20、3.62和4.62，其中，基于植被指数PRI的估算效果最佳。

图7 不同植被指数拟合的叶绿素含量估算模型Fig.7 Chlorophyll content estimation model fitted by different vegetation indices

3 讨论

水稻冠层叶片的叶绿素含量与冠层的高光谱反射率有着密不可分的联系，叶绿素含量越高，光谱反射率反而越低。近年来，将高光谱与叶绿素建立相关性进而估算叶绿素的含量已经成为研究的热点。由于高光谱数据维数多，直接建立估算模型需要的数据量与维数之间呈幂指数关系，因此，对高光谱数据的降维是研究的重中之重。

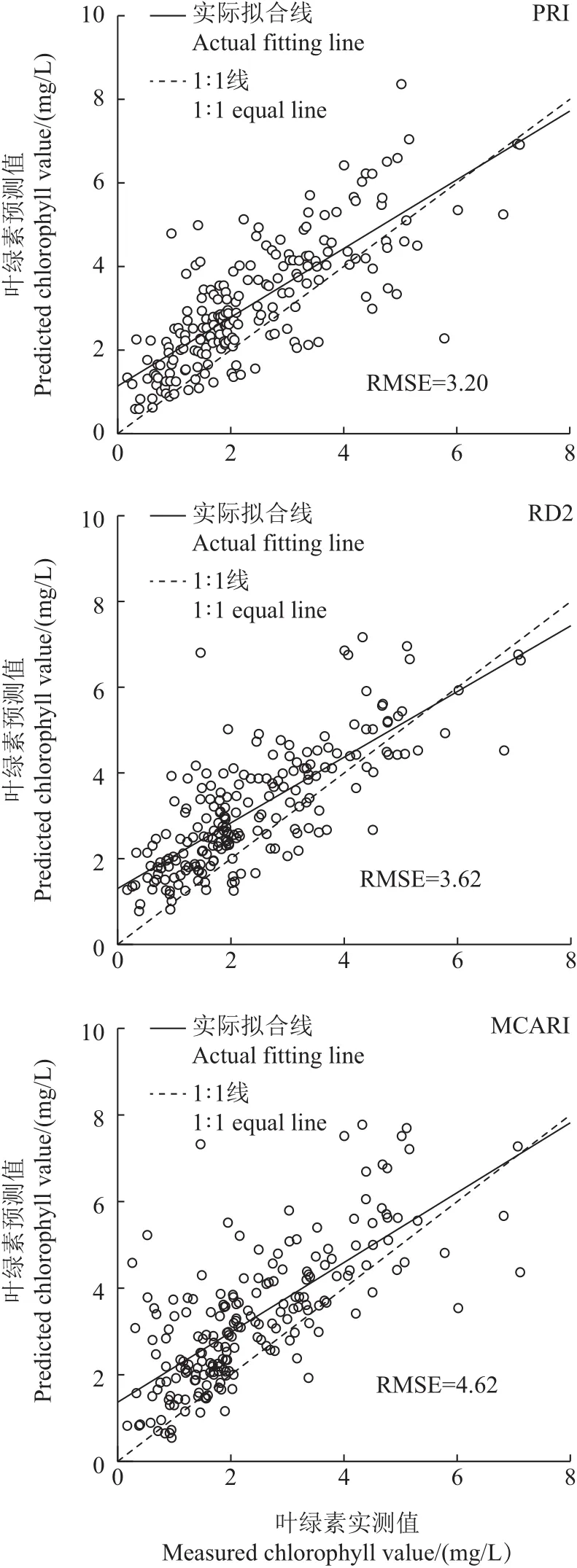
图8 不同植被指数拟合的叶绿素值验证模型Fig.8 Chlorophyll value verification model fitted by different vegetation indices

本研究表明，PRI、RD2和MCARI植被指数与水稻叶绿素的相关性分别为0.682、－0.645和－0.605，均达到极显著相关水平。利用这3种植被指数建立的估算模型的决定系数（R2）、相对误差（RE）和均方根误差（RMSE）均达到建模精度要求，验证模型RMSE分别为3.20、3.62和4.62；其中基于植被指数PRI建立的估算模型反演叶绿素效果最好，拟合方程为y=3.825e14.707x，可以对水稻进行叶绿素反演。

本文提出了一种基于主基底分析的降维方法，对降维后的光谱数据与叶绿素数据建立最小二乘回归模型，估算模型的R2为0.689，RMSE为2.20，检验模型的RMSE为1.20，相比植被指数建立的模型精度有很大的提高，估算和验证模型的误差有所降低，因而对叶绿素反演的准确性更高。

本文提出的降维方法改善了传统植被指数在选择过程中丢失大量数据的弊端，在降维的同时还能够保留光谱中起主要作用的部分，并更准确地建立光谱数据与叶绿素数据的估算模型，使得估算数据与实际数据偏差减小。

4 结论

本文利用高光谱数据对水稻冠层叶片的叶绿素含量进行了估算，提出了一种基于主基底降维的方法，为水稻中叶绿素含量高精度估算提供了科学依据。该方法选取对叶绿素敏感的400～1 000 nm波段进行Gram_Schmidt变换找到投影空间，在此投影空间下对波段进行降维，建立估算植物叶片叶绿素值的最小二乘回归模型，并与3种植被指数（PRI、RD2和MCARI）降维后建立的相同回归模型进行精度对比。结果表明：基于植被指数降维方法建立的模型建模精度和验模精度均低于基于主基底分析降维法所建立的同种模型精度，说明本研究采用的主基底分析方法对光谱数据进行降维是可行的；同时，该方法还能更好地保留原始波段的信息，改善了传统降维法的不足。因此，本研究建立的基于主基底降维的模型有较高的预测精度，对植物叶片中叶绿素含量的估算具有重要意义。