卫星在轨相对三维微角度高精度测量方法研究

贾奥男 沈海军 周徐斌 庞亚飞 姚骏

(上海卫星工程研究所，上海 200240)

卫星飞行过程中，由于外力、太阳照射、机械振动等因素的影响，有效载荷所在的基准板会发生微小的变形，从而使有效载荷在标准指向上产生小角度偏转，严重影响了高精度载荷的工作性能[1]。例如，风云四号卫星(FY-04)的闪电成像仪在轨发生的角度变化虽然只有1′～5′，但由于轨道高，对地图像移动距离达到了万米级别。

随着我国卫星事业的发展，特别是高分辨率对地观测卫星的发展，对有效载荷的指向精度要求越来越高，其微角度偏差测量的需求越来越迫切。角度测量是计量科学中较为成熟的一个分支，国内外已研制出多种测角仪器，以满足各种需要[2]。但是滚转角的高精度测量一直是精密测量技术领域的一个难题[3]。目前，滚转角测量主要有激光干涉法、偏振光测量法等，不过这些方法大都处于原理和试验阶段，距离实际工程应用还有一定距离[4-6]。而传统的地面高精度角度测量仪器或无法经受卫星发射时主动段的振动，或无法适应卫星的在轨环境，或其安装使卫星结构设计十分复杂。

盖亚(GAIA)空间望远镜[7]是欧洲航天局发射的高精密光学天文卫星，其上搭载了一套激光干涉角度测量系统，用于对GAIA卫星的两台望远镜载荷相对转角进行测量，精度达到了0.5 μrad。针对基准面的直接变形测量，文献[8]提出了基于应变测量的大型星载相控阵天线结构在轨变形测量及配准系统方案；文献[9]提出了基于位置传感器(PSD)的位移测量系统，用于测量低轨道星-2卫星(LEOStar-2)上搭载的核光谱望远镜阵列(NuSTAR)的镜面与探测器之间的相对位移变形。

在轨变形量的准确测量是结构在轨变形控制的基础，并可为图像配准系统提供修正依据，为提高卫星在轨性能提供技术保障。因此，设计制造出一种既有着小巧的机械结构，又能有较高的测量精度及分辨率的三维微角度测量仪对于解决在轨微转角测量问题提供技术手段。

本文针对航天器在轨变形问题，设计了一种能够测量两个被测物体间相对转角的方案，根据位移计测量的各面上多点的位移变化，提出了3种角度求解算法。与传统地面高精度测角仪器相比，本方案不仅适用于在轨测量，而且能同时测量三维角度。

1 测量方案

随着现代激光位移传感器技术的发展，对于微小位移的测量已经达到了很高的精度。本文提出的方案通过面的微角度旋转与由此产生的面上点的位移之间的关系，来求解相应的角度。

为了测量有效载荷偏离基准的三维角度，现设计如图1所示的测量装置(绿色与蓝色结构)。黄色物体代表星上有效载荷和基准物体，刚性悬臂分别从其上引出，用以传递发生的转动。为方便描述，称被包覆的立方为内接头，相邻的为外接面，并给外接面的各面分别命名：顶面、侧面、后面。外接面的3个面相互正交，内接头提供位移计的安装位置。

图1 初步设计的测量装置Fig.1 Preliminary designed measuring device

被测物体旋转后连带悬臂进行转动，转动后的装置如图1(b)所示。在各面上布置一定数量的位移计，对两面之间的相对位移变化进移测量，通过位移与转角之间的关系计算内接头与外接面间的相对转动，从而得到有效载荷相对基准的转角。由于位移计本身的测量结果中包含着接头的转角与平移信息，在求出转角的同时，可以进一步求出接头之间的相对平移。结合接头的转角与平移信息，可以反推出被测物体的相对平移信息。总之，即用接头之间的相对位移变化，反推出被测物体之间相对转角与相对平移。

2 数学模型

2.1 坐标系建立

在内接头和外接面上分别建立随体坐标系o-xyz和O-XYZ，其原点在各自的中心。坐标系遵循右手定则，坐标轴分别与各面垂直，如图2所示。图2(a)中两坐标系初始时重合，即内外接头的对应面相互平行。由于测量的是相对转角，假定内接头静止，外接面相对内接头旋转，此时内接头随体坐标系相当于惯性坐标系。即通过外接面随体坐标系相对于内接头随体坐标系的转动加平动来表征内外接头之间的相对位姿关系。

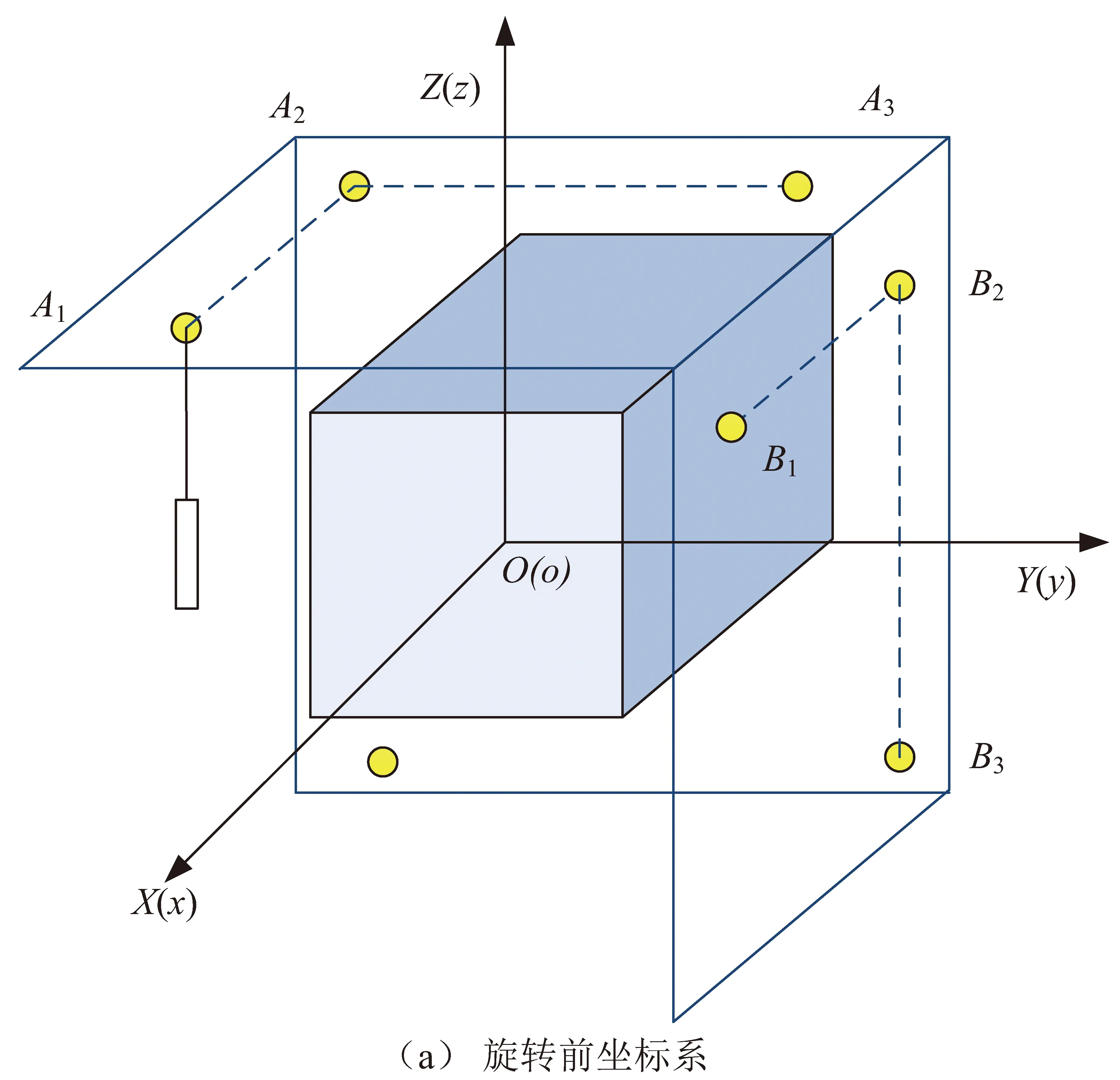
图2 坐标系定义Fig.2 Definition of coordinate system

相应的，可以得到内接头随体坐标系o-xyz下各测点的坐标：Ai=(xAi,yAi,zAi)，Bi=(xBi,yBi,zBi)，i=1,2,3。其中，测点为位移计的测量点，以激光位移计为例，测点即为光点。由三点定面的矢量叉乘运算可以得到外接面随体坐标系O-XYZ在内接头随体坐标系o-xyz下坐标轴的矢量表示。

平台顶板经过热变形后，内外接头发生相对转动，如图2(b)所示，外接面随体坐标系旋转后为O′-X′Y′Z′。假定位移计光路设置与O-XYZ的各坐标轴平行。相应的，仍可以得到o-xyz下各测点的坐标

(1)

式中：ΔhAi、ΔhBi为相应测点位移计的前后读数之差。需要注意的是，Ai与Ai′并非同一点，即转动前和转动后的测点并不相同。如图3所示，A为初始测点，AA为原测点A经过转动和平动后所到达的新位置，A′为位移计的新测点。

图3 顶面转动前后测点示意图Fig.3 Diagram of point on top surface before and after

由此同样可以得到坐标系O′-X′Y′Z′在坐标系o-xyz下坐标轴的向量表示。

2.2 相对转角求解

对于转角求解，有多种方法。假设三面上均有3个测点，根据方法需要确定所需测点。

2.2.1 解方程法

由式3.1可以得到初始状态下外接面随体坐标系的坐标轴矢量为X，Y，Z。设外接面相对于内接头随体坐标系转动的三个欧拉角为θ、φ、γ，平移量为Δx、Δy、Δz。

则通过变换矩阵[10]和平移量可以得到相对运动后的位移计原测点AAi、BBi、CCi(i=1,2,3)，以及外接面随体坐标系的坐标轴矢量X′、Y′、Z′；相对运动后的位移计新测点Ai′、Bi′、Ci′可由式(1)得到。

由平面法线和平面上一点可以得到得到平面表达式。如图3所示，由于AAi与Ai′在同一平面内，将A′的坐标带入平面表达式即可得到方程。对于侧面和后面亦是如此。

由此便得到关于θ、φ、γ，Δx、Δy、Δz的方程组。由于有6个未知数，需要6个方程。但6个方程所包含的测点必须涵盖三个面(详见2.3节)，即顶面、侧面、后面测点分配可以按3-2-1、2-2-2等形式分配。通过数值迭代的方法求解方程组，6个输入便可以得到6个输出。

2.2.2 方向余弦矩阵法

使用方向余弦矩阵[11-12]表示外接面随体坐标系与内接头随体坐标系的关系。

设o-xyz到O′-X′Y′Z′的方向余弦矩阵、o-xyz到O-XYZ的方向余弦矩阵、O-XYZ到坐标系o-xyz的方向余弦矩阵分别为H2、H1与H0。由R·H1=H2，则可以得到坐标转换矩阵为R=H2·H1-1。用θ、φ、γ定义外接面相对于内接头随体坐标系转动的3个欧拉角。按3-1-2的旋转顺序，可以求得在坐标系O-ZXY下从坐标系O-XYZ到O′-X′Y′Z′的欧拉角为

(2)

将θ1、φ1、γ1投影到坐标系o-xyz中即可得到外接面相对内接头旋转的三维角度。

(3)

2.2.3 四元数法

四元数在几何与工程应用上的重要性首先体现在它与旋转的关系上，单位四元数简洁地表示了三维空间中的旋转[13]。

取外接面顶面为例，如图4所示，可将其任意的转动分解为两次旋转：平面α1绕n转动σ1角，再绕Z′转动Φ1角，即得到平面α2。其中，平面α1为原面，法线为Z；平面α2为旋转后的面，法线为Z′；两面的交线为n；σ1为法线Z和法线Z′的夹角，即平面α1和平面α2的二面角。

法线Z和法线Z′可由测点坐标求得，于是可以得到n，σ1。由此可以写出两次转动的四元数：p1，p2。其中，p2包含未知数Φ1。对于侧面，采用同样的分解方式，可以得到两次转动的四元数q1，q2。由于顶面和侧面属于同一个外接面刚体，因此顶面的转动和侧面的转动最终效果应当一致，通过四元数乘法可得

p2p1=q2q1

(4)

通过四元数对应项相等，即可得到关于Φ1、Φ2的方程组。通过数值方法求解，便可得到Φ1、Φ2。将Φ1(或Φ2)带回原四元数，然后进行四元数相乘运算，便可得到描述整体转动的四元数。

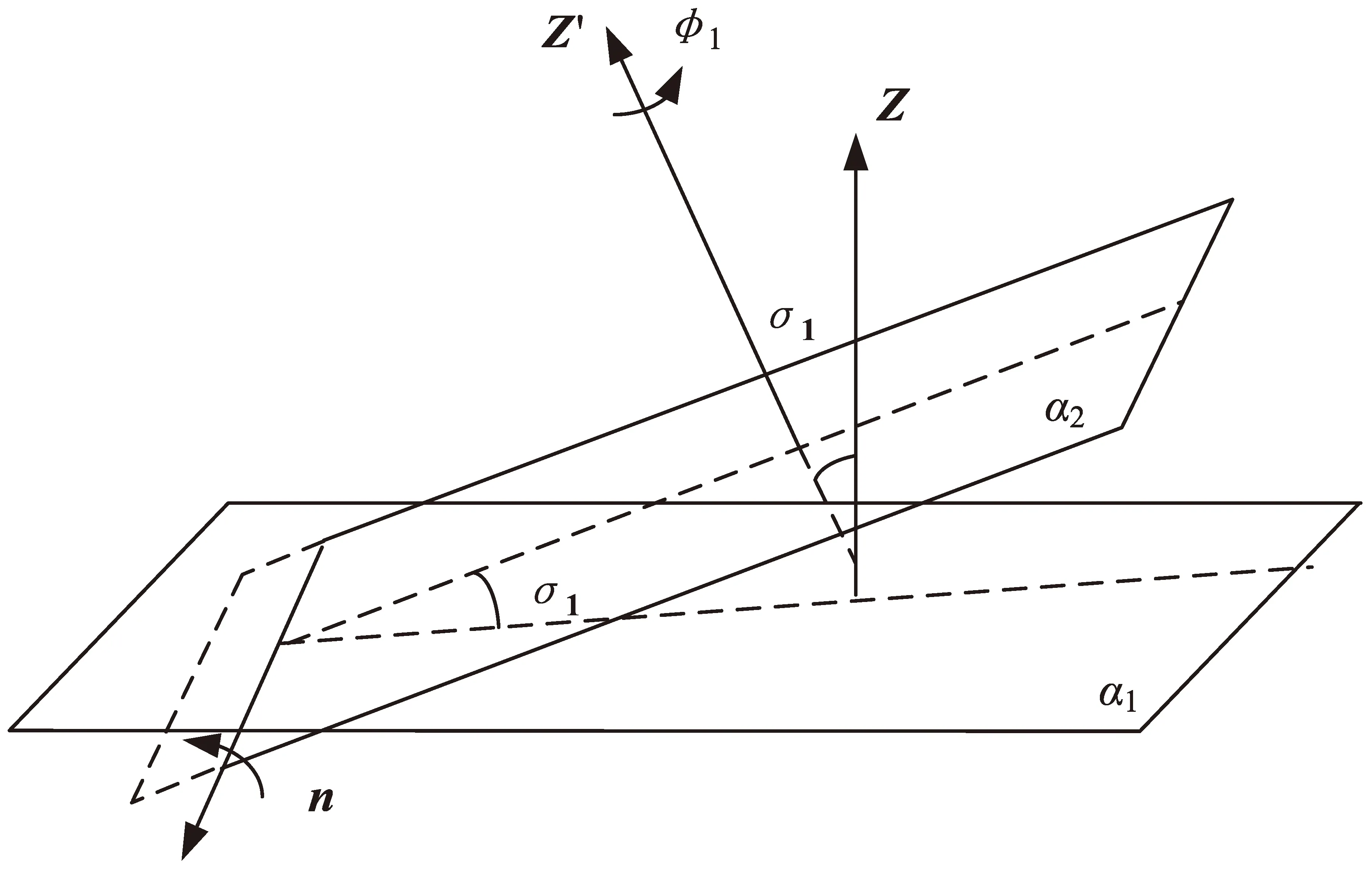
图4 顶面旋转分解图Fig.4 Rotation decomposition of top surface

2.3 平移求解

位移计读数不仅包含着角度信息，还包含着位移信息。而接头的位移则分成两部分，如图5所示：假设被测物体绕Z轴旋转，侧面上某一测点Bi到达位置Bbi；然后接头沿Y方向移动，Bbi到达位置BBi。则接头的位移分成两部分，如图5所示：d2即为因引入悬臂由旋转造成的外接面的平移，dy为被测物体y方向的位移。本节所求为总平移Δy=dy+d2。

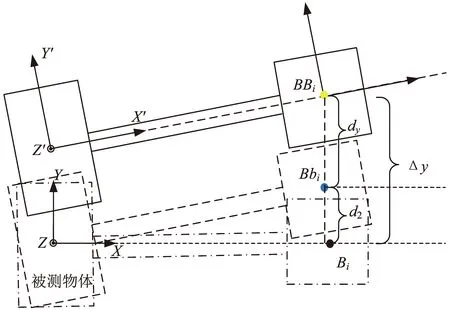
图5 悬臂而引起的位移示意图Fig.5 Displacement due to cantilever

取顶面为例，如图6所示，被测物体旋转后，顶面由原来的平面α1，变成了平面α3。把这个过程分成两部分：首先，平面α1绕内接头随体坐标系的各坐标轴分别旋转至平面α2，相应地测点从绿点位置移到了红点位置；然后，平面α2平移至平面α3，相应地测点从红点位置移到了黄点位置。而测量同一面的位移计，对于旋转，各位移计读数变化不同；而对于平移，各位移计读数变化相同，如图6所示。即指向同一面的各位移计所得到的平移信息相同。因此，为得到平移量，需3个面上的位移计信息。

对于解方程法，可以直接得到位移量。而对于方向余弦矩阵法和四元数法，由于只用到了两个测面，因此需要补充第3个面的测点。具体过程可以参照2.2.1节，与解方程法不同的是，此时θ、φ、γ已经为已知量，第3面上只需挑选一点就能获得平移量。

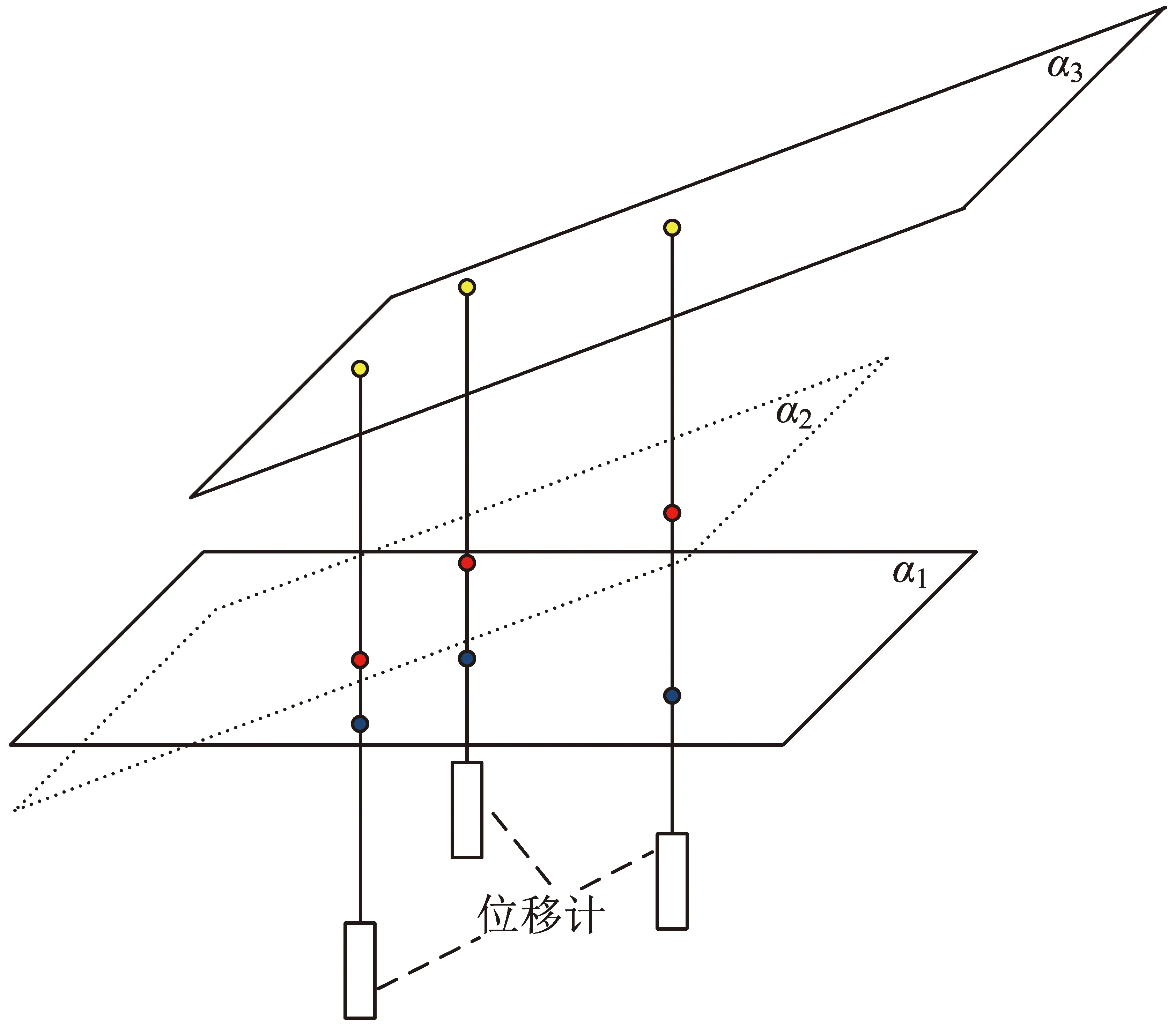
图6 旋转与平移位移计示意图Fig.6 The measures of rotation and translation by displacement sensor

2.4 相对位置确定

被测物体的转角与接头转角相同，但由于悬臂的影响，位移则有所不同。而要确定被测物体的相对位置，需要求出dx，dy，dz。由2.2节和2.3节可得到内外接头的相对转角与相对位移。进一步地，如图5所示，BBi与Bbi之间的坐标之差即为dx，dy，dz。

2.5 小结

得到位置和转角关系后便可得到被测物体之间的相对位姿(位置和姿态)。

解方程法必须用到3个面。如果仅需要测量角度，可以采用只需两个面的方向余弦矩阵法和四元数法，如表1所示。不仅可以减少装置的质量，而且可以消除由后面带来的偏转效应。不过，如果需要测量角度与位移，方向余弦矩阵法和四元数法需要7个测点。

就所需面数与测点数而言，如果仅需测量角度，方向余弦矩阵法和四元数法占优；如果需要测量角度和平移量，解方程法占优。

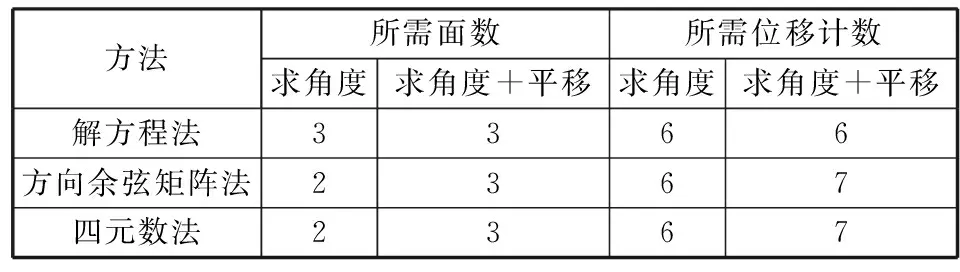
表1 各方法所需面数与测点数统计表

3 算例分析

考虑到星上的有限空间，测量装置不能过大，以及实际安装的便捷性，仿真中设单面上各测点分布在边长为100 mm的正方形的顶点，依照方法不同选择对应的测点。

3.1 仿真计算

为了验证算法的正确性，首先给定一组空间角度θ、φ、γ与位移Δx、Δy、Δz，给出理论上各位移计读数的变化量，然后代入第2节的方法中，得到θ′、φ′、γ′与Δx′、Δy′、Δz′。将得到的角度与给定的空间角进行比较，以此验证模型的正确性。

输入了多组空间角度进行验证，表中的位移量为总平移量，结果如表2所示。结果表明，计算得到的空间角和平移量与设定值吻合，证明了建模方法的正确性。而计算产生的微小偏差是由matlab软件的小数位数截断所带来的，代入计算的有效位数越多，差异越小。但相对来说解方程法出现的偏差较大，这是由方程的数值求解带来的，取决于求解过程中的循环次数。而四元数法也有方程数值求解的过程，但精度却比解方程法高，这是因为四元数法所涉及的方程较为简单。由于方向余弦矩阵有解析解，因此精度最高。

表2 仿真计算结果

3.2 参数影响分析

在实际操作中，如图1(a)所示，对于顶面而言，x和y方向的坐标可通过相对位置确定，而z方向的精确坐标，却很难通过测量手段获得。因此，必须计算其对最终测角结果的影响。

利用蒙特卡罗法进行分析，使外接面绕空间任意轴偏转某一角度，导致内外接头对应面不平行，各测点z坐标产生偏差，而求解角度时仍使用设计值，提取出多次计算所得的最大误差，如图7(a)所示。同样地，分别给各参数相应的随机误差，可以得到位移计本身测量误差、测点坐标偏差、位移计方向偏差对最终测角结果的影响，分别如图7(b)(c)(d)所示。

可以看到，在各参数人为可控的范围内，初始位置对结果的影响远大于其他参数。因此必须保证测点的坐标精度。

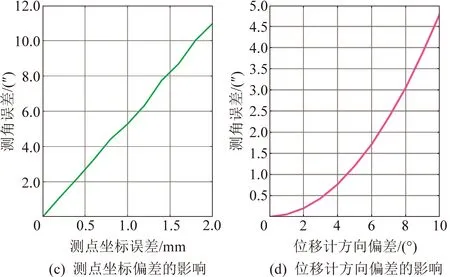
图7 各参数偏差对测角结果的影响Fig.7 Influence of deviation of each parameter on measurement results

4 试验验证

试验系统采用色散共焦位移传感器，精度为0.3 μm，如图8所示，通过质量块加载，使平台蜂窝板发生变形，从而使两边的被测物体发生微转动，以模拟星上发生的变形。随着组数增大，质量块的质量逐渐增加。

试验中设置两面均为3个测点，用最小均方误差(LMS)采集位移计数据。内接头为边长200 mm的立方壳。在一被测物体上安装自准直仪，对面的另一被测物体安装棱镜，达到测量相对转角的目的。同时为了增加精度，按上述方法布置两台，进行相互对照。以自准直仪的测量结果为对照，以方向余弦矩阵法进行结果求解。

图8 试验系统Fig.8 Experimental system

4.1 试验结果

图9为各组偏摆角的测量结果；图10为各组下俯仰角的测量结果；图11为各组俯仰角与偏摆角的综合结果，同一个圈内为同一加载条件下的结果。

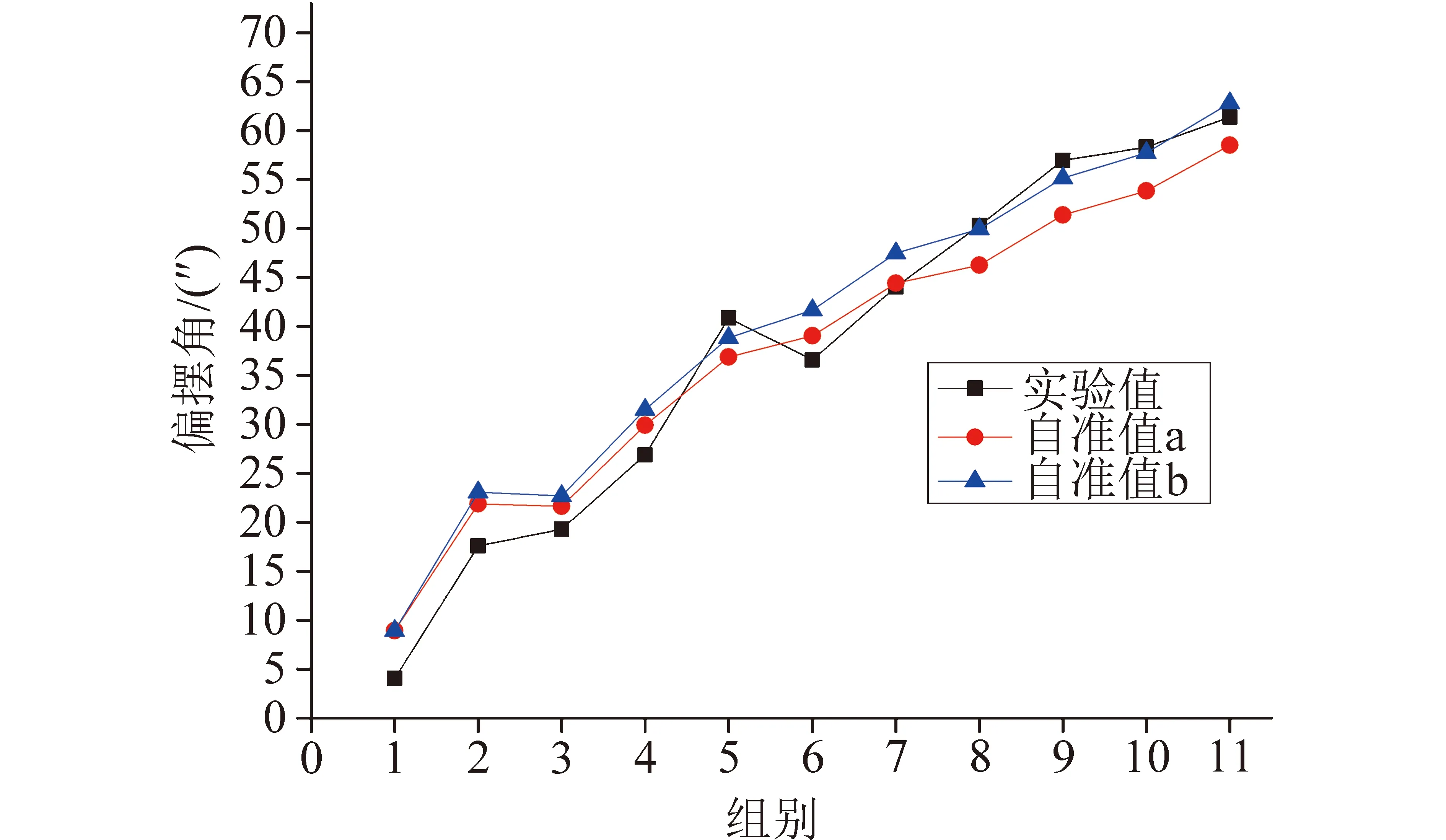
图9 不同加载质量下的偏摆角Fig.9 Bending angles of different loading quality

图10 不同加载质量下的俯仰角Fig.10 Pitch angles of different loading qualities

可以看到，两台自准直仪所标定的转角本身就有所不同，而且随着测量角度的增大，这个偏差有进一步扩大的趋势。这是因为自准直仪a与棱镜b是有一段距离的，如图12所示。棱镜的安装误差导致两自准直仪的测量坐标系不同，即两自准直仪所测角度并非绕同一轴的转角。而蜂窝板的变形会导致被测物体的微变形，使自准直仪a与棱镜b所在位置的局部变形不一致，导致读数发生偏差。

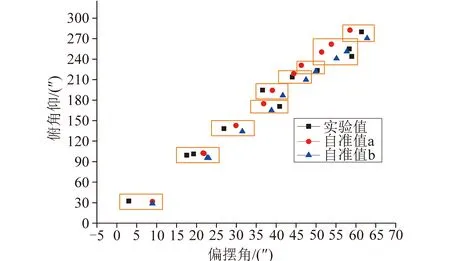
图11 偏摆角与俯仰角的综合结果Fig.11 Combined results of yaw angles and pitch angles

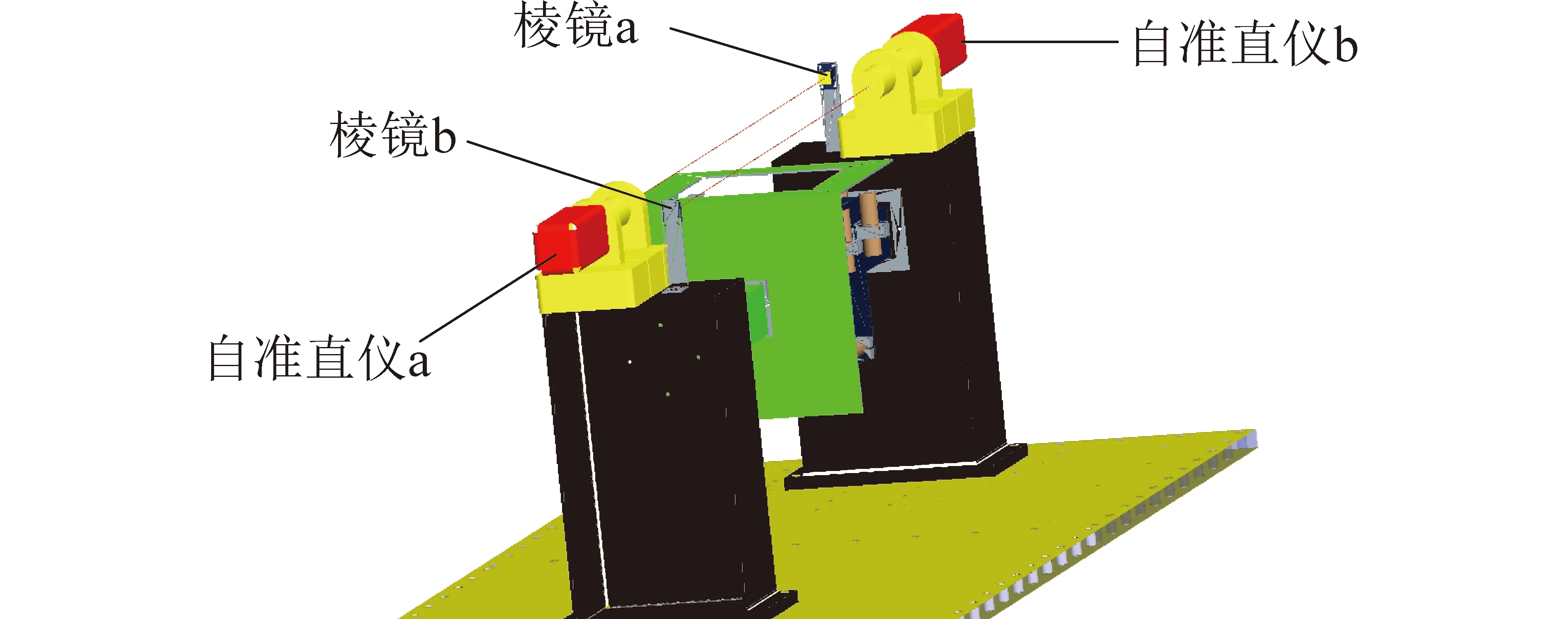
图12 自准直仪示意图Fig.12 Layout of self-collimator

图13表示角度的偏差值，其中横坐标为偏摆角偏差值，纵坐标为俯仰角偏差值。由于悬臂位于自准直仪a与棱镜b中间，所以俯仰角与偏摆角的基准值采用两自准直仪所测角的平均。由图13可以看出两个角的误差基本稳定在5″以内。

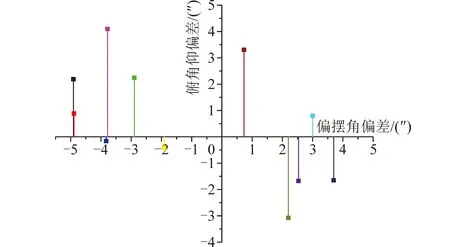
图13 不同加载质量下的偏差结果

4.2 误差分析

首当其冲的就是位移计本身的测量误差。而计算中的各项参数均采用设计值，在试验中由于位移计的夹持方式显然无法达到要求。测点的坐标预估在各方向上有+1 mm的误差；位移计方向与设定指向在空间中估计有1°的偏差；初始位置下内外接头对应面不平行，约有1°的偏差。此外，当边界条件发生变化时，由于重力导致悬臂弯曲变形会带来一定的影响。误差结果符合3.2节的分析。

5 应用展望

由3.2节的分析可知，内外接头的初始位置对测量精度的影响较大。在地面标定后，经过主动段，需要在轨开机查看位移计读数，据此调整数学模型的初始位置，然后进行求解。

不过，该方案建立在悬臂为刚体的基础上。由于在轨环境恶劣，在交变的温度场下，如果悬臂本身发生热变形，将会导致较大的测角误差。因此，对于悬臂结构的稳定性设计将是日后研究的重点。此外，位移计能否在真空中正常使用也将直接影响装置的精度。

针对某些因空间障碍无法直接测量的部件，可以通过第三者采用多个装置组成链式传递的方式。不过参与的部件增多，精度将有所下降。

由于在轨有效载荷指向精度测量不需要绕自身指向轴的旋转角，在这种情况下，可以将本方案的两个面退化为一个面，即可测出二维角度。

6 结束语

原理样机验证试验中，俯仰角与偏摆角的测量精度在5′的视场内分别达到了4″和4.9″。而误差的很大一部分原因是由于试验中一些初始参数设置没有进行精确保证，如(测点坐标、位移计方向等)。如果进一步使这些参数靠近设计值，精度将会进一步提高。实际应用中应优先保证对角度求解影响大的参数——测点坐标。后期将基于以上研究内容进行方案优化。

在轨变形测量满足目前卫星的高精度发展的迫切需求，发展前景广阔。该装置结构简单、性能稳定、测量精度较高，可以在卫星仪器安装板底部位于有效载荷的正下方设计相应接口，或直接在有效载荷上设计相应接口，实现在轨相对三维角度测量。