基于季节调整与神经网络融合算法的售电量预测
● 国网湖南省电力有限公司经济技术研究院 陈耀红 陈火焱 徐彬焜 国网湖南省电力有限公司 陈 勇 陈 翔
针对月度售电量波动性大、随机性强、精准预测困难的特点,本文构建了一种结合数据预处理 (X11加法模型)和BP神经网络算法的预测模型,结合宏观经济及自然环境采用历史售电量、固定资产投资、梯度温度等输入参数进行月度售电量预测。实际结果表明,基于X11-BP神经网络融合算法进行售电量预测,能够较好模拟月度售电量的波动性,比单一BP神经网络预测精度更高,可为电网公司和售电企业生产经营及规划计划管理提供重要数据参考。
1 方法介绍
1.1 季节分解
时间序列季节调整是对时间序列中隐含的因季节性因素造成的影响加以纠正的过程。季节调整的方法有X11方法、CensusX12方法、移动平均法、Tramo/Seats方法。本文主要采用X11方法中加法模型,如式1所示。

其中:Tt是趋势项,St是季节项,It是随机项。
经季节调整后的数据列分出三个子序列,包括长期趋势列、季节因素列、不规则因素列(随机列)。通过分离时间序列中季节变动因素和不规则要素,使得数据中的长期趋势序列符合不同月份之间具有可比性的特征,从而能及时反映数据的趋势变化,分析预测的结果更为可靠。
1.2 神经网络算法
BP神经网络算法具备多层次的前向反馈特性。首先数据信息前向传播,通过隐含层进行逐层计算,然后传送至输出层。通过判断输出层获得的结果不是期望值时,进入反向传播,即按照误差大小从输出层经隐含层逐步向输入层调整各阈值及联结权值,直至预测值不断接近或等于给定值。
反向传播算法的步骤可概括如下:
(1)选定权系数初值。
(2)重复下述过程,直到误差指标满足精度要求,

其中:E表示总误差函数,Ek表示第k个样本的误出项网络和单元k的实际输出k, 然后k=2,...,N 过程。 反向过程:对各层(l=L-1 到 2),对每层各单元,计算差,ε表示精度。
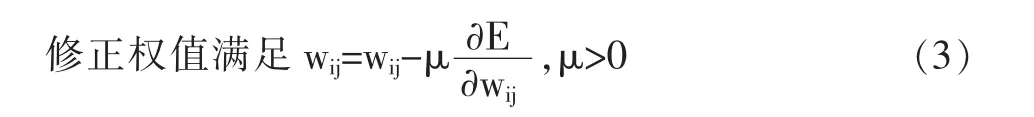
对k=1到N正向过程计算,计算每层单元的节点输
其中:wij表示修正权值,μ为修正系数。
(3)结束。
1.3 X11-BP神经网络融合算法
考虑到月度售电量数据不仅受经济发展、生产活动季节性、气象等常规因素,还受抄表、政策变化等偶然因素的影响,因而使用X11季节调整与BP神经网络相融合的算法,对月度售电量进行季节分解,将分解后的长期趋势列、季节因素列和随机项列分别进行BP神经网络计算。其中,通过相关性分析寻找不同序列的关键影响因素,将各个关键影响因子与相关分解序列进行BP神经网络训练。具体构建步骤如下:
(1)外生变量选取。以宏观经济为切入口选取GDP、CPI、PPI、固定资产投资和产品产量等经济指标作为待选影响因子,筛选出月度固定资产投资与月度售电量趋势性因素有很好的相关性。
以自然因素为切入点,选取温度梯度分类统计月度天数,低温高温异常温度月度天数、降水月度均值等指标作为待选影响因子,筛选出温度梯度分类统计月度天数和降水月度均值与月度售电量随机序列有较好的相关性;而低温高温异常温度月度天数与月度售电量季节性因素序列有很好的相关性。
(2)数据归一化。由于数据量纲不同,在进行具体运算前对数据进行归一化处理,数据归一化处理也可以保证程序运行时加快收敛速度。
(3)隐含层神经元数确定。本文采用人为经验判断和留一交叉验证法来确定隐含层神经元的数量,人为经验判断法是依据隐节点数一般是远小于训练样本数的经验,用同一样本集对具有不同隐节点数的网络进行训练,直到权值不再变化网络稳定为止,然后依据测试误差最小,确定网络的隐节点数;留一交叉验证法是按照有N个样本的情况下,留一个样本,剩下的用来训练,如此重复N次,这样来选择参数,之后利用全部N个样本和选择好的参数来训练,进行外推预测。
(4)训练次数确定。训练次数直接影响网络的泛化能力。本模型采取措施为在训练过程中每经过一定训练次数后,停止训练并测其测试误差,将每次获得测试误差及相应的权值保存,直到测试误差开始上升时,网络便达到了最佳训练次数,相应的权值便具有最佳的泛化能力。
2 实证分析
2.1 月度售电量的季节分解
月度售电量是典型的隐含季节性因素的时间序列。以H地区电网售电量为例,从假期及气温因素分析,受春节因素影响每年1~3月售电量有所波动,4~6月保持相对平稳水平,7~9月因夏季高温天气影响达到一年中月电量峰值,10月因国庆假期及气温下降影响月电量回落,11、12月因低温天气影响月电量又有所上升。考虑经济指标对售电量的影响,随着经济指标的波动,每年环比月度售电量均有不同程度的变化,整体以增长趋势为主,体现为年度曲线不断上移。
通过以上分析,得出在研究的样本期内月度售电量呈现出典型的季节性特征,短期内受假期、气温等周期性因素的影响,中长期主要受区域内经济发展变化的影响。另外,抄表周期因素可能会对月度售电量预测造成干扰。因此,采用X11加法模型对月度售电量进行季节分解,可将影响售电量波动性的影响因素进行剥离。X11加法模型分解出的季节性、长期趋势性和非常规因素等3个序列具体见图1。

图1 月度售电量的季节分解结果
2.2 模型构建及结果分析
基于季节分解和1.2节中选取的外生变量,构建季节分解X11-BP神经网络融合算法模型。实例中采用2006年1月至2017年8月H地区的售电量、投资、不同梯度异常温度数据作为输入参量,进行训练、测试模型,从而预测2017年9~12月度售电量。
将2006年1月至2016年12月作为训练集,2017年1~8月售电量作为验证集,结果显示季节分解-BP神经网络融合算法模型的售电量整体模拟偏差在1.3%以内。将灰色预测、单一BP神经网络算法与季节分解X11-BP神经网络融合算法的预测结果进行对比,结果表明灰色预测效果最差,某些月份出现17.7%的偏差率,单一BP神经网络相对灰色预测效果较好,最大偏差率为8.1%,X11-BP神经网络融合算法预测效果最好,最大偏差率仅为1.3%,且平均偏差率0.1%,具体数据见表1。
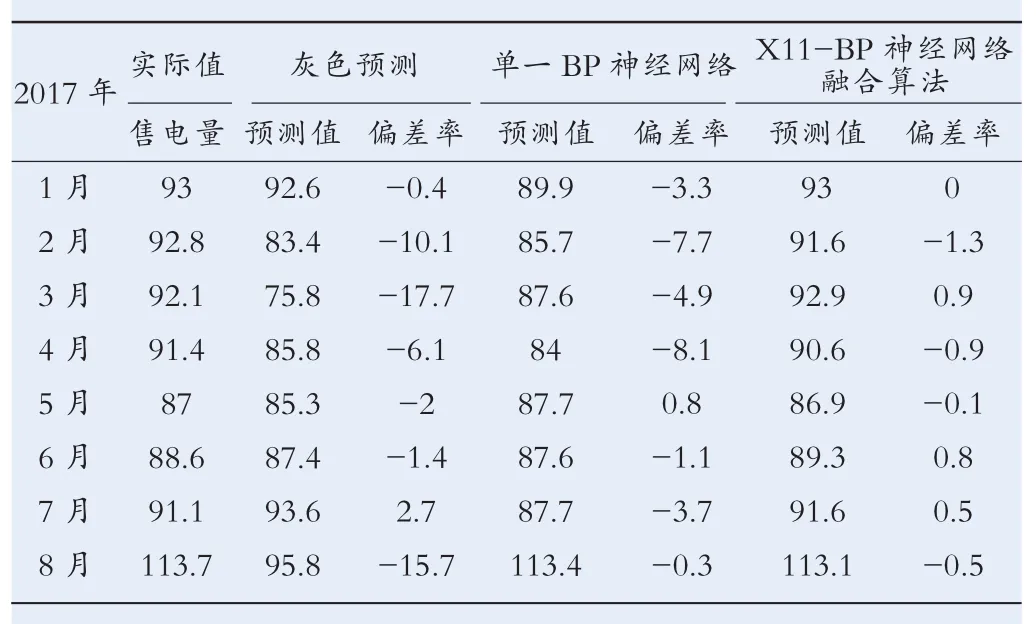
表1 不同模型拟合对比 亿千瓦时,%
基于X11季节分解-BP神经网络融合算法,得出2017年9~12月预测售电量合计375.7亿千瓦时,具体每月售电量预测结果如图2所示。
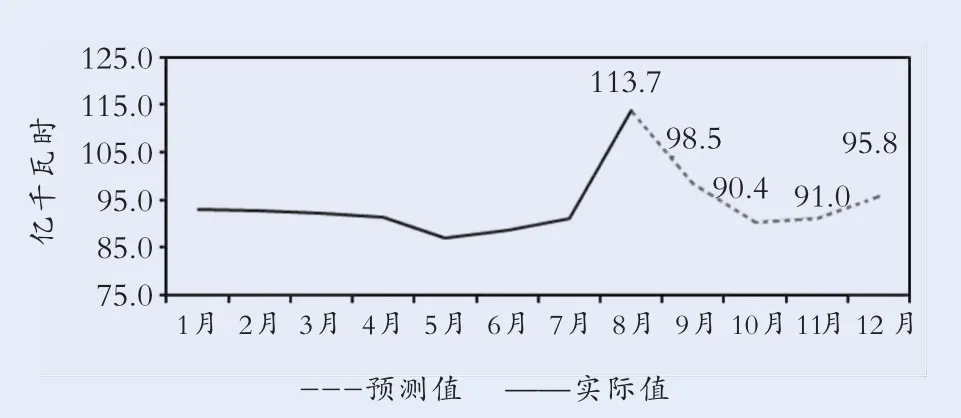
图2 基于X11季节分解-BP神经网络融合算法预测结果
3 结束语
本文构建基于X11季节调整与BP神经网络融合算法的售电量预测模型,较好的预测了月度售电量波动性,达到了较高预测精度。验证结果表明,基于季节调整与BP神经网络融合算法的预测精度最高达到98.7%,比传统预测方法的预测精度更高,具有一定的实用价值。

