周期性公司正常化估值的理论框架与模型构建

陈 蕾（博士生导师），于 田

一、引言

经济增长总是在平衡与不平衡的矛盾运动中呈波浪式前进，继而形成经济周期。不同行业变动时，也往往随之呈现出明显、可预测的增长或衰退格局，只是与宏观经济周期波动之间的关系密切程度存在差异。其中，周期性行业作为一个运动状态与宏观经济波动相关性较强的行业，在经济处于上升时会紧随其扩张，在经济衰退时也会相应衰落。周期性公司因此具有收益波动性大、预测难度高等特征，导致其估值问题成为国内外企业价值评估领域的难题。加之周期性公司在我国国民经济中的地位举足轻重且转型升级态势凸显，其在兼并重组中的估值问题日益成为理论界和实务界共同关注的焦点。这些都对周期性公司估值体系的完善提出了要求。

已有研究表明，即便是选择适用性较强的收益途径[1]对其进行估值，在利用两阶段永续模型评估第二阶段收益额时仍然容易出现较大偏差。对此，陈蕾、于田[2]提出，在周期性公司第二阶段的收益额预测情形不够明朗的情况下，采用退出倍数法有利于提高周期性公司估值的有效性。而在此基础上，结合此类公司特征尝试引入正常化估值思路，对收益法两阶段永续模型进行改进，力求进一步完善周期性公司估值方法体系。

立足此研究视角进行文献梳理发现，目前有少量文献涉及对正常化估值思路的初步探讨与应用研究，目的是提高周期性公司估值的合理性；其中，“正常化”有时也被称作为“平滑化”“平均化”或“标准化”。比较具有代表性的是，Aswath Damodaran[3]提出，在周期性公司估值中，可以对现金流折现法的因子进行正常化，即采用正常化的现金流、增长率和折现率，估算其正常化价值；陈蕾[4]也强调，正常化（或标准化）的收益额就是周期性公司在正常年份即周期中段年份的收益额，此时的收益额、折现率、增长率等指标受宏观经济的影响可忽略不计，近似达到周期性公司收益的一种内在稳定状态，其具体数额可根据历史长周期数据进行分析估计，而与之相匹配的折现率也应考虑选用正常化的折现率。此外，也有部分学者针对企业收益额这一单一因子，指出对其进行平滑化处理，有助于提高收益预测的合理性。例如，顾朝阳（Gu Z.Y.）[5]发现，收益平滑化处理能够提高企业未来现金流量预测的准确性，即收益平滑化程度越高，企业未来现金流的波动性越小；张国清、夏立军和方轶强[6]发现，平滑历史收益数据，有助于预测企业未来的盈利能力，提高会计盈余与企业价值的相关性；谭峻、赵亮和王智鹏[7]认为，在对矿业公司这一类典型周期性公司的收益额进行预测时，由于收益波动周期较长，有必要长周期或跨周期对金属价格和投资回报率进行平滑化处理。

通过以上研究，可以了解正常化估值思路应用于公司估值的理论依据，只是这些研究的理论系统性和操作指导性尚显薄弱，以至于该方法尚未在公司估值实务中得以广泛、有效地使用。鉴于此，本文拟基于现有研究，从基本思路、基本模型、应用步骤、适用范围和注意事项等方面，构建正常化估值思路应用于周期性公司估值的理论框架，结合案例，设计、模拟、比较周期性公司正常化估值的三种具体模型并提出选择建议，以此为该类公司估值的方法选择与实务操作提供参考。

二、周期性公司正常化估值的理论框架构建

（一）周期性公司正常化估值的基本思路

对于当前公司估值中常用的收益法两阶段永续模型，目标公司在第一阶段的预期收益额通常较为明朗，在第二阶段则达到或近似达到稳定状态，其收益额一般是永续年金形式或永续增长形式。但是，周期性公司在第二阶段的预期收益额通常无法达到稳定或近似稳定的状态，因为其收益更易受宏观经济的影响，呈现出一种上下反复的周期性运动，所以传统的两阶段永续模型无法合理地体现第二阶段的收益水平。

事实上，周期性公司正常化估值的实质，就是合理估算周期性公司的正常化价值，同时结合目标公司在评估基准日位于收益周期的具体阶段及其经历完当前这一完整收益周期的时间，综合判断目标公司在评估基准日的时点价值。即可以采用改进后的两阶段永续模型，假定目标公司在第一阶段期末，刚刚经历完一个完整的收益周期，其不是收益周期的波峰或波谷，而是恰好达到周期中段年份（以下简称为“基准年”），此后进入第二阶段的新一轮收益周期并循环反复，如下图所示。可见，目标公司在第一阶段期初的收益现值，就是该公司从评估基准日至新一轮周期基准年的各年预期收益额的现值合计，该值可以通过分析公司历史财务数据和预测未来若干年可能的盈利情况测算确定；目标公司在第二阶段期初的收益现值，则可视为该公司的正常化价值，需要根据其历史收益的长周期或跨周期数据的起伏状况，分别建模估计正常化的收益额、稳定增长率和折现率，以减少收益剧烈波动导致的价值严重高估或低估问题。

周期性公司收益周期示意图

（二）周期性公司正常化估值的基本模型

首先，根据周期性公司正常化估值的基本思路，其基本模型可以表示为：

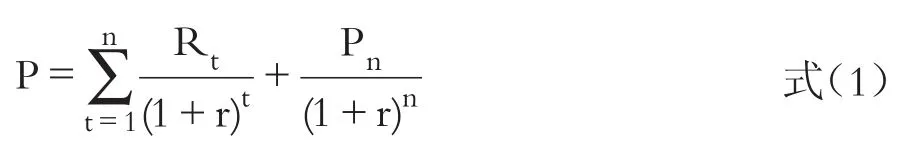
式中，P为目标公司评估值，Rt为未来第t个预测年期的收益额，r为当期折现率，t为收益预测年期，n为第一阶段收益预测期限，第n＋1年亦即目标公司新一轮收益周期基准年，Pn为目标公司正常化价值。

其次，结合永续年金模型和永续增长模型的公式，周期性公司正常化价值（Pn）可以分别用公式表示为：

式中，An为正常化的收益额，gn为正常化的稳定增长率，rn为正常化的折现率。

综上，周期性公司正常化估值的基本模型可根据其收益额增长特征，进一步表示为：

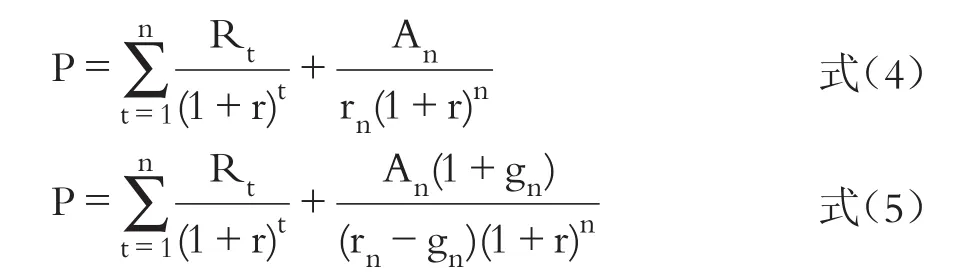
其中，当目标公司的正常化稳定增长率gn=0时，式（3）等同于式（2），式（5）等同于式（4）。

不难看出，对周期性公司收益周期的判断及其正常化价值（Pn）的测算是周期性公司正常化估值的重点，而在此过程中对价值因子（An、gn、rn等）的正常化进一步成为周期性公司正常化价值测算的难点。对此，本文将在第三部分深入探讨周期性公司正常化价值及其因子的具体测算模型，对基本模型予以细化。

（三）周期性公司正常化估值的应用步骤

1.确定新一轮收益周期基准年。对目标公司未来收益进行判断，通常需要参考企业的经营和财务状况以及生命周期、近期投资计划、经营风险水平、外在宏观经济走势等因素，以此选取一个正常年份即收益周期中段年份作为两阶段的分割点。如果直接将当期年份作为基准年，而忽视了目标公司自身的历史情况与现处周期阶段，会导致估值结果不准确；如果选取的基准年处于收益周期的波峰或较高位置，会造成目标公司的价值高估；如果选取的基准年处于收益周期的波谷或较低位置，则会造成目标公司的价值低估。因此，应避免以上三种情况的发生。

2.测算目标公司第一阶段收益现值合计值。一是分析目标公司的历史财务数据，预测基准年之前若干年的盈利状况及各年预期收益额；二是估算目标公司折现率，将各年预期收益额进行折现求和。这一步的具体分析和测算方法与传统收益法无异。其中，企业自由现金流、股权自由现金流、息税前利润、息税摊销折旧前利润、净利润等不同的净现金流或利润指标是可供选择的预期收益额口径；加权平均资本成本、权益资本成本是可供选择的折现率口径，需要注意二者口径的一致性。

3.选取正常化估值的历史周期区间测算目标公司正常化价值。选取正常化估值的历史周期区间，需要分析目标企业历史收益的波动规律。这一区间应当恰好涵盖目标企业一个完整的历史收益周期，且应距离评估基准日较近。其长度可以短至5年左右，也可以长至10年左右，但通常以后者更为常见。在此之后，可以采用绝对平均测算模型、相对平均测算模型或近似年金测算模型等具体模型测算正常化价值。

4.计算目标公司评估值。将目标公司第一阶段收益现值合计值以及目标公司正常化价值（Pn）等代入式（1），可以计算得到目标公司价值（P）。但如果目标公司存在非经营性资产或溢余资产，则需要将此评估值再加上评估基准日的非经营性资产评估值和溢余资产评估值，以此作为目标公司价值的最终评估结论。

（四）周期性公司正常化估值的适用范围

周期性公司正常化估值思路的应用价值，一是避免了应用收益法时因公司长期收益额难以预测所形成的估值困扰，二是充分利用了历史财务数据来提升整体估值的可信度，三是合理兼顾并妥善处理了公司当期位于收益周期的具体阶段与基准年之间可能存在的差异。所以，该思路无疑为周期性公司估值提供了新的有效路径。但是，在周期性公司正常化估值过程中，通常需要对历史收益的长周期或跨周期数据的起伏状况进行分析，据此测算目标公司的正常化价值，因此，正常化估值思路更适合于成立时间较早、已经具有长期经营纪录的周期性公司；对于经营期有限或经营纪录曾发生变化的周期性公司，其适用性会相应减弱。

（五）周期性公司正常化估值的注意事项

1.关于正常化估值的完整性。在测算目标企业正常化价值时，容易进入的误区是只对部分因子例如收益额进行正常化处理，而其余的因子仍采用当期数据。这就会把周期性公司的正常化收益与衰退年份或繁荣年份提取的其他指标数据相混淆，从而造成估值不合理。正确的正常化估值，除了需要对收益额进行正常化处理，也应当对折现率、稳定增长率等因子进行正常化，还可能涉及对融资成本、资本回报率、再投资率等具体指标数据的正常化，这才是完整的正常化估值。

2.关于是否考虑通货膨胀。如果选取一个完整历史周期区间的收益数据，测算目标公司在新一轮收益周期基准年的正常化价值，那么可能存在一个疑问，即是否应当考虑通货膨胀？为解决此问题，可以通过简单举例予以说明。假设基准年正常化收益额为A0，每年通货膨胀率为it，则预期年收益为Rt=A0（1+it）n；假设正常化折现率为r0，受通货膨胀影响，折现率变为 rt=（1+r0）（1+it）-1。于是，考虑通货膨胀的估算模型可表示为：

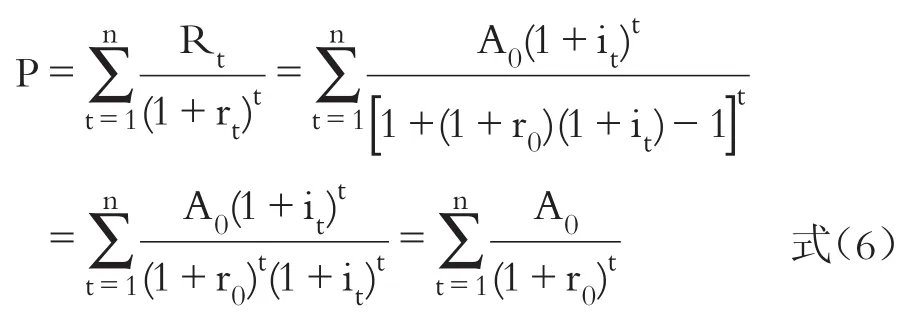
由式（6）可知，对目标公司采用现行价格水平进行未来收益预测时，如果其价格水平仅受通货膨胀的影响，则这种影响可以在价值估算过程中得以抵消，即最后估值结果不会因为是否考虑通货膨胀而存在差异。

三、周期性公司正常化价值的具体测算模型及案例分析

下文将重点针对式（1）中的正常化价值Pn以及式（4）和式（5）中正常化收益额An的测算问题展开讨论。具体结合周期性公司估值案例，设计、模拟并比较绝对平均测算模型、相对平均测算模型和近似年金测算模型这三种具体模型并提出选择建议，以对前文提出的周期性公司正常化估值的基本模型予以细化。

（一）绝对平均测算模型及案例分析

1.基于绝对平均测算模型的收益额正常化。均值是统计学中最基本、最常用的一种平均指标。估算目标公司正常化收益额最简易的方式，就是将已选定的历史周期区间内的历史收益额数据直接进行平均化处理。用公式表示为：

式中，m为历史周期区间期限，Rt为历史周期区间内第t年的历史收益额。

2.关于折现率和稳定增长率的正常化。折现率的正常化通常需要关注目标公司在较长时间跨度里的资本成本。如果目标公司的资本结构和资本成本在很长时间内都没有发生较大变动，那么可以直接以此判断正常化的折现率。反之，需要进一步采用正常化的无风险报酬率、风险报酬率、负债率、债务资本成本等具体指标判断正常化的折现率。例如，可以采用长期国债收益率取代当期利率作为无风险报酬率，采用历史周期区间内的市场平均风险溢价等计算风险报酬率。同样，稳定增长率的正常化，亦可根据目标公司在历史周期区间内的历史增长规律进行统计分析和具体判断。关于折现率和稳定增长率的正常化问题，在后续探讨其他三种具体测算模型的过程中并无实质差异，故不再赘述。

3.基于绝对平均测算模型的案例分析。下文将结合某个周期性上市公司（以下简称“ZC公司”）正常化估值的案例，对绝对平均测算模型进行模拟应用。假设评估基准日为2017年12月31日，评估对象为ZC公司股东的全部权益价值，其在2008～2017年间的经营状况如表1所示。

测算目标公司的正常化价值，首先需要选取正常化估值的历史周期区间。根据1995～2016年我国GDP的增长走势，该公司在2009年及2015年形成了两个低谷，并且平均9年左右会形成一个完整的经济波动周期；再结合ZC公司2008～2016年的经营状况，可以看出，ZC公司在2009～2015年恰好经历了一个完整的收益波动周期，与宏观经济走势基本吻合，加之此时段距离评估基准日较近，故将2009～2015年选定为ZC公司正常化估值的历史周期区间。

其次是对收益额、折现率、稳定增长率等因子的正常化。将ZC公司在2009～2015年间的各年度股权自由现金流（FCFE）的数值分别代入式（7），计算得到正常化的股权自由现金流为：

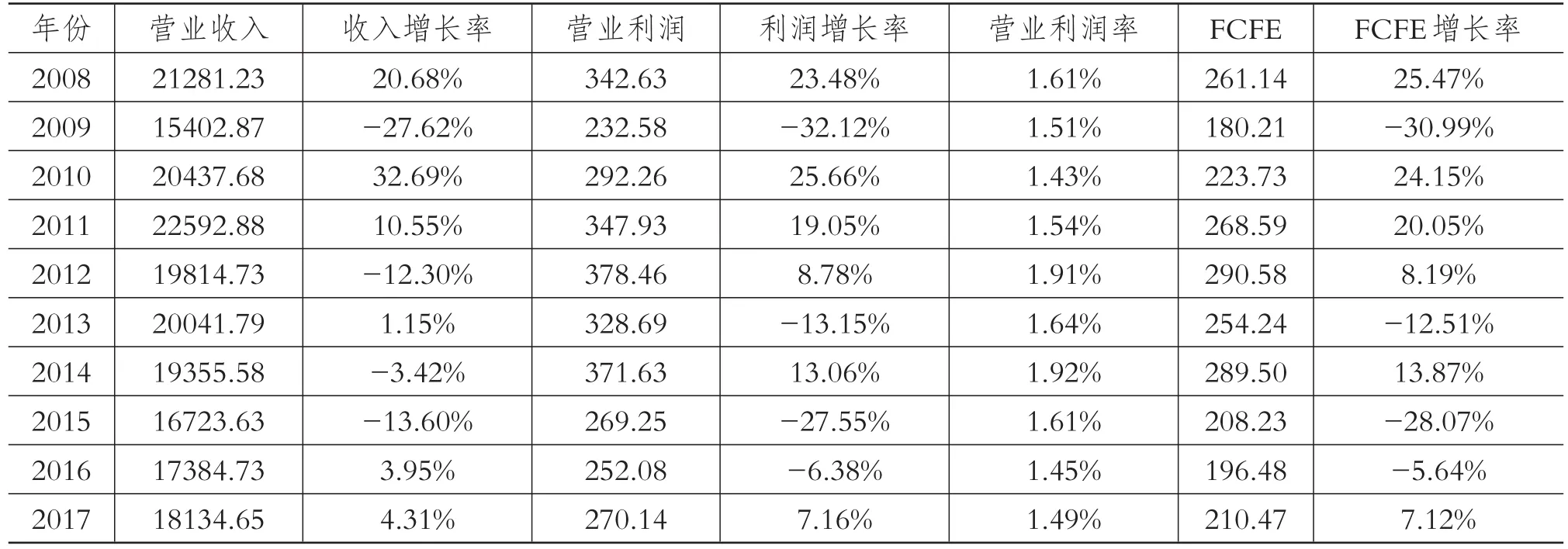
表1 2008～2017年ZC公司经营状况 单位：百万元

同时，综合考虑ZC公司在2009～2015年间的投资回报率、股权风险溢价、收益增长率等指标的波动特征和期间均值，将正常化的折现率rn和正常化的稳定增长率gn分别取值为8%和2%。

最后，将An、rn、gn一并代入式（3），计算得到ZC公司的正常化价值为：

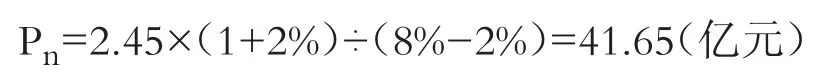
（二）相对平均测算模型及案例分析

1.基于相对平均测算模型的收益额正常化。为解决绝对平均过程中可能存在的尺度问题，本文继续引入相对平均测算模型，即计算一段时期内该变量缩小版指标的平均数。该种方法更加注重各个指标的比率而非绝对值，例如应用一段时期的利润率指标取代净利润予以平均化，再将平均利润率与正常化的营业收入或基准年相近年度（如第n年）的营业收入预测值相乘，以此求得正常化收益额。对于资本性支出、营运资本等指标也可以采取这种做法，即将一段时期内各指标与收入或账面资本的比率进行平均化，而不是直接将绝对值平均化。

以利润率为例，正常化的营业利润可以用公式表示为：

式中，pt为历史周期区间内第t年的营业利润率（营业利润/营业收入），In为第n年营业收入或正常化的营业收入。

2.基于相对平均测算模型的案例分析。继续以ZC公司的正常化估值为例，对相对平均测算模型进行模拟应用。假设ZC公司在第n年的营业收入预测值为190亿元，预计没有投资收益、营业外收入和营业外支出，企业所得税税率为25%。将ZC公司在2009～2015年间的各年度营业利润率分别代入式（8），计算得到正常化的营业利润为：

据此，可进一步求得ZC公司正常化的净利润为：3.14×（1-25%）=2.36（亿元）。将此数值与 rn=8%、gn=2%一并代入式（3），计算得到ZC公司的正常化价值为：

（三）近似年金测算模型及案例分析

1.基于近似年金测算模型的收益额正常化。在现实估值活动中，企业在稳定期的未来预期收益虽然比较稳定，但大多数情况下，并不一定表现为绝对等额的年金收益，而是表现为有窄幅波动的非年金收益。此时，可以利用年金现值系数将每年不等额的非年金收益转化为近似年金收益，再进行资本化处理求取评估值。对于周期性公司我们同样可以借助这一思路，将其在历史周期区间内的各年不等额的非年金收益转化为近似年金收益即正常化收益额，进而测算周期性公司的正常化价值。公式为：

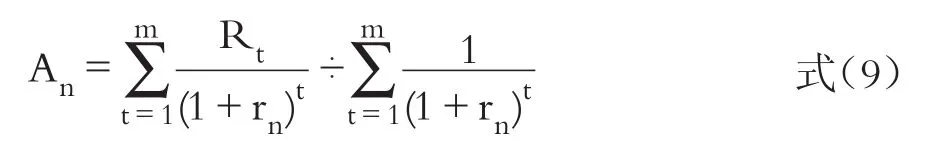
式中，前半部分表示目标公司在历史周期区间内的非年金收益“现值”合计值，后半部分表示目标公司在历史周期区间内的折现系数之和，即年金现值系数。将二者相除，即可得到被视为正常化收益额的近似年金收益。

2.基于近似年金测算模型的案例分析。仍然以ZC公司的正常化估值为例，对近似年金测算模型进行模拟应用。将ZC公司在2009～2015年间的各年度股权自由现金流（FCFE）数值与rn=8%分别代入式（9），计算得到正常化的股权自由现金流如下，详细计算过程见表2。

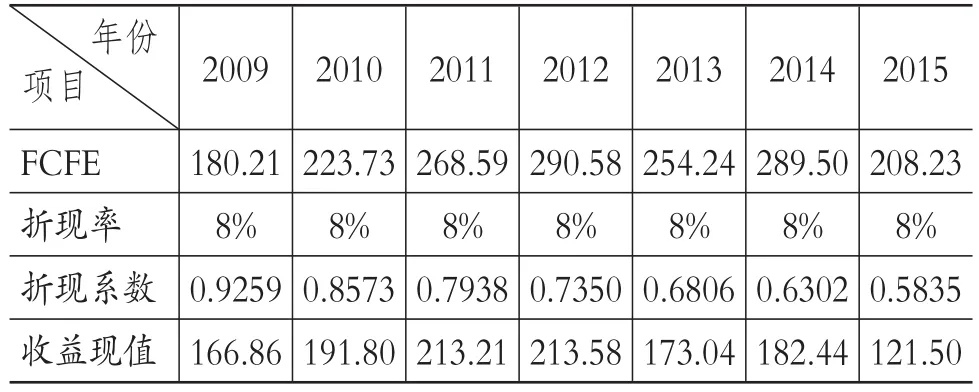
表2 2009～2015年历史收益及其“现值”单位：百万元

将An=242.48百万元≈2.4亿元、rn=8%、gn=2%一并代入式（3），计算得到ZC公司的正常化价值为：

Pn=2.4×（1+2%）÷（8%-2%）=40.80（亿元）

（四）不同测算模型的比较与选择

通过比较可以看出，无论是哪种测算模型，关键都在于对历史收益进行适当的平滑化处理，并配以正常化的折现率、增长率等因子，从而测算目标公司正常化价值。基于三种测算模型所展开的案例测算结果基本趋于一致，这种相互验证也从侧面说明将上述模型用于测算周期性公司正常化价值的适用性。然而，不同测算模型具有各自不同的优缺点，在具体估值实务中必须结合目标公司的实际情况合理选择使用。

例如，绝对平均测算模型最为简便直观、易于操作；相对平均测算模型能够解决绝对平均过程中可能存在的尺度问题，但计算相对复杂，需要进行正常化处理的指标相对较多；近似年金测算模型有效地考虑了目标公司在历史周期区间的收益波动情况，更适合于收益呈窄幅波动、异常值不多的周期性公司。

四、结论

正常化估值思路为周期性公司估值提供了新的有效路径，但相关研究的理论系统性和操作指导性尚显薄弱。本文从基本思路、基本模型、应用步骤、适用范围和注意事项等方面系统构建了正常化估值思路应用于周期性公司估值的理论框架，并结合案例，设计、模拟和比较周期性公司正常化估值的三种具体模型，最终提出选择建议。研究结论如下：

一是恰当运用正常化估值思路，可以在应用收益法时避免产生因公司长期收益额难以预测所形成的估值困扰，充分利用历史财务数据来提升整体估值的可信度，合理兼顾并妥善处理了公司当期位于收益周期的具体阶段与基准年之间可能存在的差异。但是，正常化估值思路更适合于成立时间较早、已经具有长期经营条件的周期性公司；对于经营期有限或经营纪录曾发生变化的周期性公司，其适用性会相应减弱。

二是对收益周期的判断和正常化价值的测算是周期性公司正常化估值的重点，而在此过程中对收益额、折现率、稳定增长率等因子的正常化进一步成为周期性公司正常化价值测算的难点。在具体估值实务中，估值人员可以结合不同测算模型的优缺点和目标公司的实际情况，合理选择采用绝对平均测算模型、相对平均测算模型、近似年金测算模型等方法估计周期性公司的正常化价值。

希冀上述研究结论和相关建议能够在一定程度上促进周期性公司估值方法体系的完善，同时为周期性公司估值方法的选择与实务操作提供借鉴。当然，本文重点讨论的是正常化估值思路在周期性公司收益法估值中的应用，而该思路在公司估值的其他方法或环节中可能也具有一定的适用性，且周期性公司正常化价值的测算应当不局限于以上三种具体模型，这些都可以成为本选题的下一步研究方向。