Prediction of MBR Membrane Pollution Based on Improved PSO and Fuzzy RBF Neural Network
TAO Ying-xin, LI Chun-qing, SU Hua
Prediction of MBR Membrane Pollution Based on Improved PSO and Fuzzy RBF Neural Network
TAO Ying-xin, LI Chun-qing, SU Hua
(College of Computer Science and Software, Tianjin Polytechnic University, Tianjin, China)
In order to improve the prediction accuracy of MBR membrane flux, using a fuzzy Radial Basis Function neural network to establish a network prediction model, and use the improved Particle Swarm Optimization (PSO) algorithm to optimize. The functional equivalence of the fuzzy inference process and the RBF neural network is used to unify the system function. When using a modified PSO algorithm to train a fuzzy RBF neural network, First, using the improved PSO algorithm to obtain the initial weights and thresholds of the fuzzy RBF neural network, and then perform a second optimization on them to get the final weights and thresholds. The experimental simulation results show that this method of this paper shortens the response time, has a small steady-state error, and can better fit the expected value of the membrane flux and better predict the membrane flux.
MBR; PSO; RBF
0 Introduction
The membrane bioreactor (MBR) is a new wastewater treatment technology, which combines membrane separation technology with bioreactor technology. Membrane flux is an important parameter in the MBR study. Membrane flux reflects membrane fouling. The prediction of membrane pollution through the establishment of prediction models has become an important research direction in MBR simulation. Most of the commonly used prediction models have some defects, such as insufficient analysis of the membrane fouling mechanism and poor prediction accuracy.In this paper, the improved PSO algorithm is used to optimize the fuzzy RBF neural network so that the experimental results of the simulation system are closer to the prediction results.
1 Improved PSO and Fuzzy RBF Neural Network
1.1 Fuzzy RBF neural network
RBF neural network as a good feedforward neural network has global approximation ability. It is superior to backpropagation neural network in terms of approximation ability, classification ability and learning speed. Combining RBF neural network with fuzzy control, utilize the function equivalence of the fuzzy inference process and the RBF neural network to unify the system function. The structure of the fuzzy RBF neural network is shown in the figure.
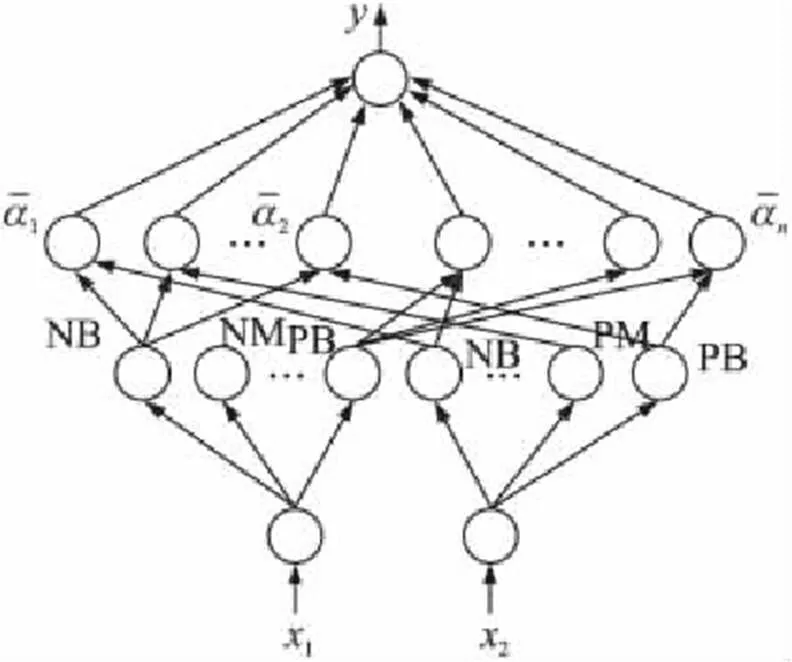
Fig.1 Fuzzy RBF neural network structure model


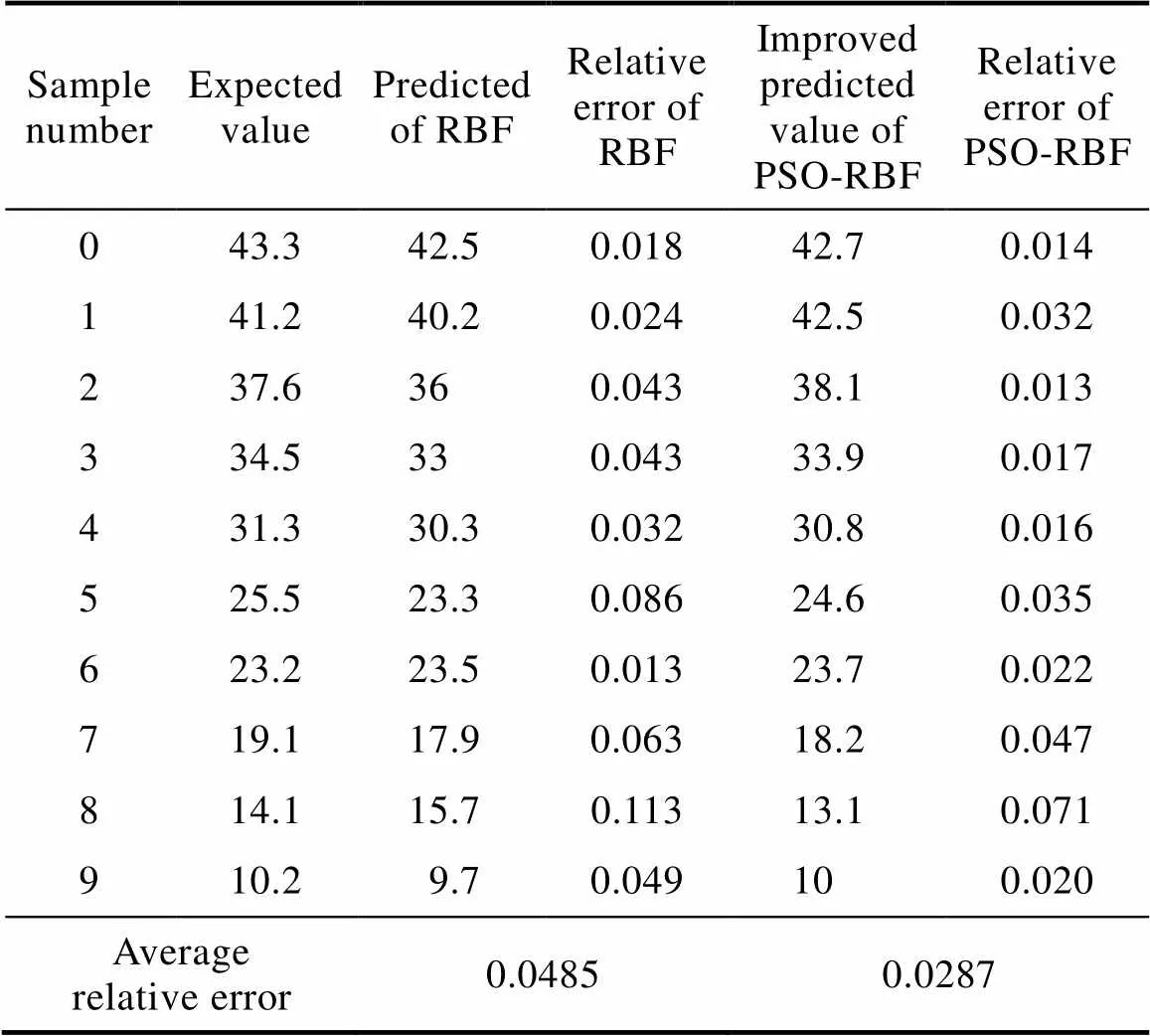
Tab.1 Comparison of membrane flux prediction results
In this equation: X1 is the membership function, X2 and X3 represent the center and width of the membership function, respectively. The number of nodes in this layer is 16. Layer 3 is the rule layer, and each node represents a fuzzy rule. Its role is to match the premise of fuzzy rules, and calculate the applicability of each rule. Which is

In this paper, the “multiply” operator is used to complete the simulation and normalized calculations are performed at the same time, which is
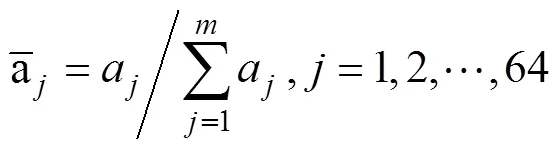
The fourth layer is the defuzzification layer, which is the output y, which is used as a predictor of the flux of the membrane. which is
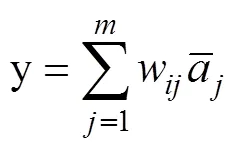
1.2 Standard PSO Algorithm
The standard PSO algorithm is a heuristic search technology with simple implementation, strong global search capability and superior performance. The standard PSO algorithm uses a speed-position search method in which all particles have been performing search motions in parallel. By recording the best position of each particle so far and simultaneously communicating the local information between the particles, the best solution so far for the entire particle group or domain is obtained. The flow chart is shown in Figure 2. Expressed as a mathematical model
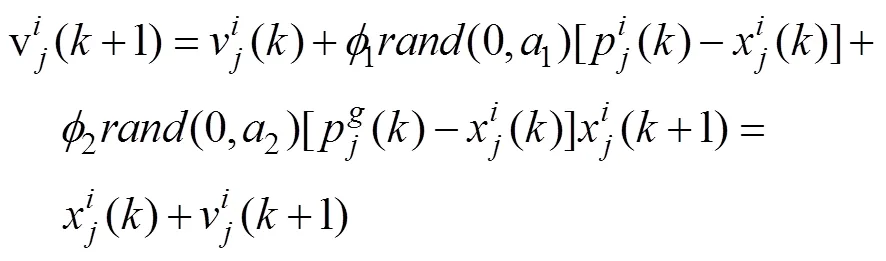
In the formula: i=1, 2,…, m represents the number of the particle; j=1,2,…, n is the j-th component of the n-dimensional vector; and represent the velocity vector and position vector of particle i in k iterations, respectively; are the learning rates that control the relative contributions of individual cognitive component and social component of the group, respectively; g denotes the particle number with the global best fit value so far; and generate a uniform distribution of random numbers between S and M, respectively. Its introduction will increase the randomness of the cognitive and social search direction and the diversity of algorithms, a1, a2 are the corresponding control parameters. represents the current position of the i-th particle, relative to the distance of the particle so far to the optimal position , represents the current position of the i-th particle, relative to the distance of the particle so far to the optimal position .
1.3 Improved PSO algorithm
The standard PSO algorithm has a fast search speed and high efficiency, but it also has many shortcomings, such as the existence of premature convergence or prematurely falling into local extremum, which makes the search speed of the whole algorithm slower and sometimes stagnate.For this reason, this paper proposes an improved PSO algorithm, trying to expand the global search ability and improve the local search accuracy.Practice shows that if the PSO algorithm is iteratively linearly decremented, the local search accuracy in the later iteration can be enhanced, thereby improving the convergence performance of the algorithm.Often adopt the following formula
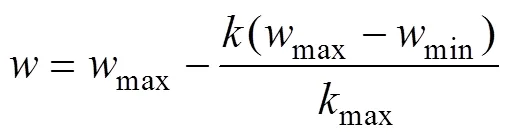

From the standard PSO algorithm, the current position of the particle and the current velocity determine the position of the next moment, so the particle will update its velocity and position by iterating to move closer to the optimal position. However, if this optimal location is a local optimal location, the particle swarm cannot be searched again in the solution space and thus falls into a local optimum. If the genetic algorithm is used to modify the global extremum P by referring to the genetic algorithm at this time,then the direction of the particles will change, so that you can enter other areas to search, and you can find the optimal solution by looping.This is the basic idea of the PSO algorithm.In order to make the PSO algorithm have better optimization performance, this paper introduces a random operator to make the particle group perform the mutation operation with a certain probability q under the condition of satisfying the variation. The calculation formula of q is as follows
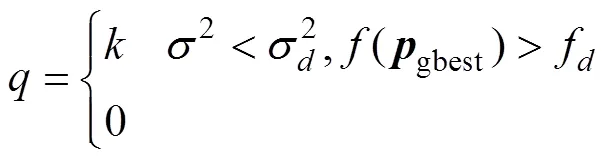
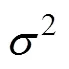

1.4 Improved PSO and RBF neural network algorithm
The fuzzy RBF neural network learning method has strong nonlinear mapping ability and is a good learning method.What it needs to solve is a complex non-linearization problem. The weight of the network is gradually adjusted in the direction of local improvement. This will cause the algorithm to fall into local extremum and lack globality. At the same time, the adjustment of its convergence is also determined by the choice of initial state. The PSO algorithm has better global search ability. When training the fuzzy RBF neural network, a combination of the two is adopted. Firstly, the initial weights and thresholds of the fuzzy RBF neural network are found by using the PSO algorithm, and then the initial weights and thresholds are used for the second optimization to obtain the final weights and thresholds. The specific steps are as follows:
Initialize the particle swarm first according to initial conditions and constraints.
(2) Determine the initialization speed, position and population size of the particle swarm, learning factor, inertia weight, and number of iterations.
(3) Determine the fitness function of the particle swarm. In this paper, the mean square error of BP neural network is used as a fitness function. Its formula is as follows:
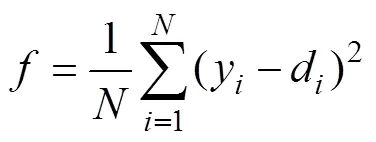
In the formula: N is the number of samples for network training, X1 is the actual output value of the i-th sample, and X2 is the expected output value of the i-th sample.
(4) Calculate the fitness value of each particle in the particle swarm. According to formula (6), the fitness of each particle under network training is calculated. In this paper, the network excitation function is taken as the sigmoid function.
(5) Extreme update. The fitness of each particle is compared with the fitness of the local best position, and if it is better, it is the best position at present. For the global extremum, the fitness of the particle is compared with the global optimal fitness. If it is better, the current fitness value of the particle is taken as the global optimal fitness value of the population.
(6) Speed update. The position and velocity of the particles are updated according to equations (1) to (3).
(7) Mutation operation. Calculate the mutation probability according to Equation (4) and perform the mutation operation according to Equation (5).
(8) Iteration stops. The iteration is stopped when the iteration reaches the error requirement or the number of iterations reaches the maximum number of times.The weights and thresholds obtained at this time are then substituted into the network for secondary optimization, otherwise, go to step (3) to continue the iteration.
Figure 3 is the change curve of fitness of PSO and improved PSO algorithm after the mean squared error is equal to 0.002. It can be seen that the PSO algorithm got into a local optimum when iterating 14 times.For the improved PSO algorithm, due to the addition of mutation operations, the particles entering the local optimum are searched into other regions. Although the convergence rate is reduced, the local convergence ability is enhanced and the training ability of the neural network is improved.
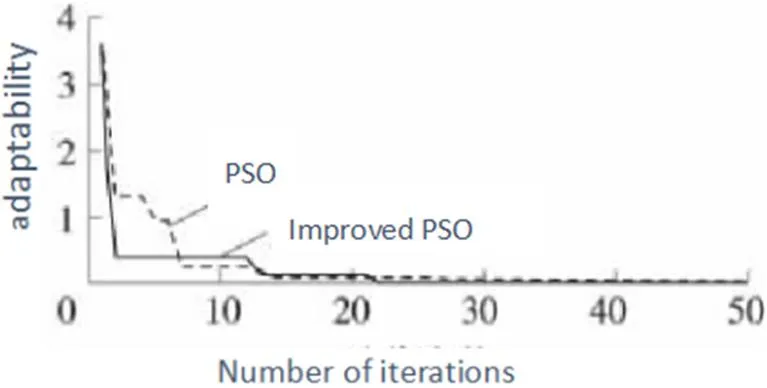
Fig.3 Fitness curve
2 Application of the algorithm in MBR membrane pollution prediction
2.1 Application of the algorithm in MBR membrane pollution prediction
In order to verify the effectiveness of the fuzzy RBF neural network optimized by PSO algorithm in this paper, the MBR membrane pollution prediction accuracy is improved. The membrane bioreactor is used as the research object, and the transfer function is as follows
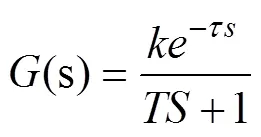
In the formula: T=10, k=9, setting temperature is 24°C. For a fuzzy RBF neural network controller, first we use the expected rate of flux and flux of the membrane flux as input, and the actual flux of the membrane as output. The performance index of BP neural network online learning is
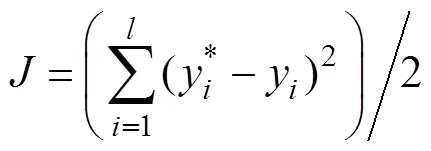

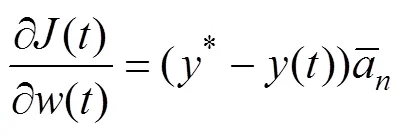
2.2 Analysis of experimental results
A simple RBF neural network prediction model is established under the same training conditions, and the relative results of the improved PSO and fuzzy RBF models are used to obtain the prediction results.
Table 1 shows the comparison table of predicted membrane flux prediction results. As can be seen from the table, the average relative error of the prediction model of the unoptimized RBF algorithm is 4.85%, while the average relative error of the prediction of the fuzzy RBF optimized by the improved PSO is 2.87%.
It can be seen by comparing Figure 4 that the simulated RBF neural network optimized by the improved PSO algorithm enhances its own learning adaptability, has a small steady-state error, and can well fit the output of the reference model. The control effect is significantly better than the traditional RBF algorithm model prediction results.
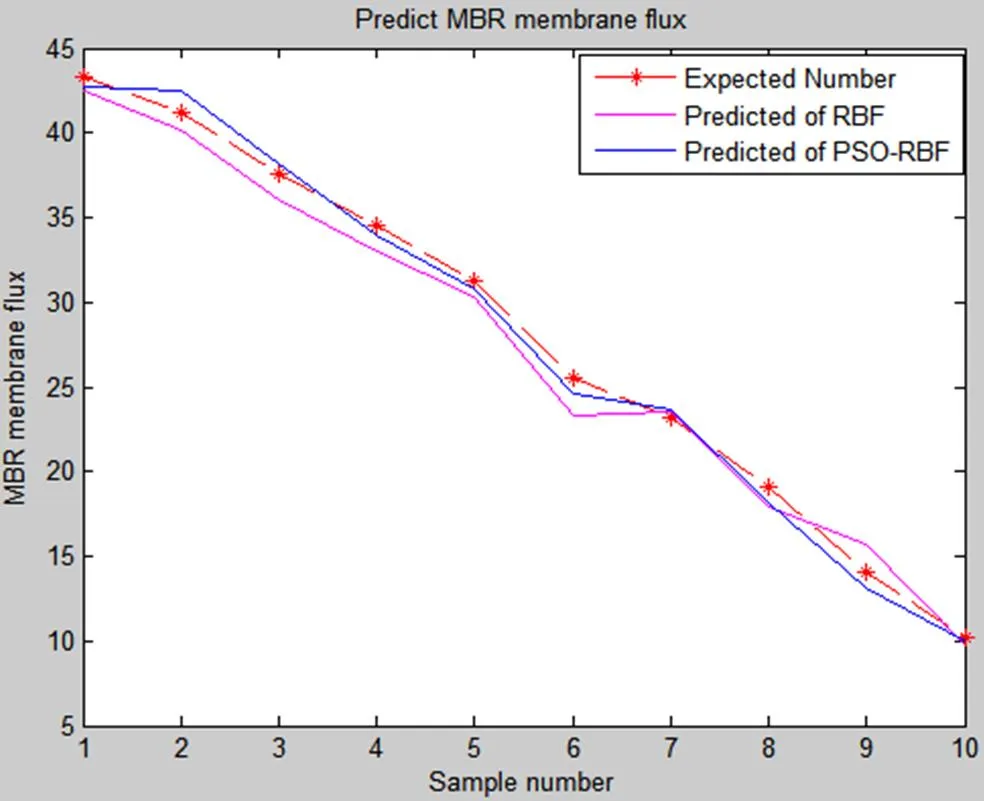
Fig.4 Comparison of prediction results
3 Conclusion
In this paper, the PSO algorithm is applied to the fuzzy RBF neural network, so that it has a stronger nonlinear approximation ability.
At the same time, it overcomes the problem that the standard PSO algorithm is easy to fall into the local minimum, improves the self-learning and self- adaptive ability of the fuzzy RBF neural network, and improves the transient and steady-state performance of the system.It is proved that the fuzzy RBF neural network optimized by PSO algorithm is feasible in MBR membrane pollution prediction simulation and has achieved good prediction results.
[1] IYAN Hong-ying, LI Chun-qing, 2013. Study on Intelligent Simulation and Prediction Method of MBR Membrane Fouling[J]. Journal of Computer Measurement and Control, 21(8): 1-5.
[2] TANG Jia, LI Chun-qing, 2016. Study on Simulation and Prediction of MBR Fouling Based on RBF Neural Network Optimized by Genetic Algorithm[J]. Software Engineering, 19(9): 11-13.
[3] Zhang Dingxue, Guan Zhihong, Liu Xizhi. 2006. A RBF Neural Network Learning Algorithm Based on PSO and Its Application[J]. Computer Engineering & Applications, 42 (20): 13-15.
[4] ZHANG Jian, LIU Ding-Yi. 2014, A Method of Optimizing RBF Neural Network with PSO. Computer Simulation, 31(11): 269-272.
[5] Li Jie-jia, Li Xiao-feng, Xie Jin-xiang, 2014. Temperature Control of Annealing Furnace Based on Improved PSO and Fuzzy RBF Neural Network[J]. Acta Metallurgica Sinica, 38 (3): 337-341.
[6] Liang Kai. 2017. Application of Support Vector Machine Based on Simulated Annealing Algorithm in MBR Membrane Pollution[D]. Tianjin University of Technology.
[7] ZHANG Zhi-yu, ZHAO Dan-guo, HOU Xiao-yu. 2013. Application of PSO-RBF Neural Network in Prediction of Urban Water Demand[J]. Hydropower Energy Science, (6): 55-57.
[8] Xie Yugui, Zhong Shaodan, Wei Yuke. Improved particle swarm optimization and convergence analysis[J]. Computer Engineering and Applications. 2011, 47(1): 46-49.
[9] Ren Zihui, Wang Jian. An adaptive example group algorithm for dynamically changing inertia weights[J]. Computer, 2009, 36(2): 227-229,25.
基于改进的PSO和模糊RBF神经网络的MBR膜污染预测
陶颖新,李春青,苏 华
(天津工业大学计算机科学与软件学院)
为了提高对MBR膜通量的预测精度,采用模糊径向基函数(RBF)神经网络建立网络预测模型,并采用改进的粒子群(PSO)算法进行优化。采用模糊推理过程与RBF神经网络所具有的函数等价性,统一系统函数。在利用改进的PSO算法对模糊RBF神经网络进行训练时,先利用改进PSO算法得到模糊RBF神经网络的初始权值和阈值,然后对其进行二次优化得到最终的权值和阈值。实验仿真结果表明:本文的这种方法,缩短了响应时间,稳态误差很小,能够与膜通量的期望值更好的拟合,更好的预测膜通量。
MBR;PSO;RBF
TP39
A
国家自然科学基金(51378350);国家青年科学基金(50808130)
陶颖新(1992-),女,硕士研究生,主要研究方向:MBR计算机模拟仿真,大数据;李春青(1962-),男,博士,主要研究方向:MBR计算机模拟仿真,大数据云计算;苏华,女,硕士,主要研究方向:计算机网络,可信计算。
本文著录格式:陶颖新,李春青,苏华. 基于改进的PSO和模糊RBF神经网络的MBR膜污染预测[J]. 软件,2018,39(8):52-56
10.3969/j.issn.1003-6970.2018.08.012

