农村基础设施投资公平性测度方法
文/王秉鼎,山西财经大学会计学院
1 极差
极差:样本数据中最大值与最小值的差,它可以部分反映样本数据的离散程度。一般而言,当用极差来反映公平程度时,极差越大,就越不公平。但极差只利用了样本中的两个极端值,并不是样本整体数据离散程度的全面真实反映,而且易受通货膨胀因素的影响,因而,极差并不是一个很好的统计指标。
2 变异系数
变异系数:在计算数据的分散程度时,样本标准差是一个使用较为普遍的统计指标。但是样本标准差数值的大小一方面取决于原变量值本身水平的高低的影响,也就是与变量的均值大小有关,变量值绝对水平高的,离散程度的测度值自然就更大,绝对水平低的,离散程度的测度值自然也就更小;另一方面,它们与原变量值的计量单位相同,采用不同计量单位计算的变量值,其离散程度的测度值也就不同。为消除变量值水平高低和计量单位不同对离散程度测度的影响,需要计算变异系数。如果用σ表示样本标准差表示样本平均值,则变异系数的计算方法为CV=σ/。通常CV的取值范围为0到1,CV=0就说明所有样本个体取值相同,当然也就意味着绝对公平;一般而言,变异系数的数值越大,不公平的程度就越高。
3 基尼系数
世纪初意大利经济学家基尼,根据洛伦茨曲线找出了判断收入分配平等程度的指标(如下图),设实际收入分配曲线和收入分配绝对平等曲线之间的面积为A,实际收入分配曲线右下方的面积为B。并以 A 除以 A+B的商表示不平等程度。这个数值被称为基尼系数或称洛伦茨系数。
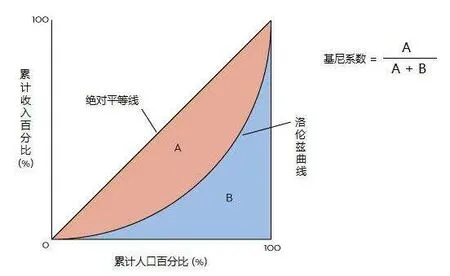
图1 洛伦兹曲线
在实际计算时,其计算公式为:

其中Mi为某一收入水平组人口数累积百分比,Qi为某一收入水平组输入数累积百分比。基尼系数的取值范围为0-1, 等于零则意味着完全公平;等于 0则意味着完全不公平。
基尼系数由于使用了所有样本数据,并且对通货膨胀不敏感,因而它是一个很好的反映公平程度的统计指标。对基尼系数而言,并没有设定一个公平程度的标准,只能说基尼系数越小,公平程度就越高。在使用基尼系数反映收入不平等程度时,联合国有关组织规定:若低于0.2表示收入高度平均;0.2-0.3表示比较平均;0.3-0.4表示相对合理;0.4-0.5表示收入差距较大;0.6以上表示收入差距悬殊。
4 泰尔指数法
泰尔指数法(Theil 指数):泰尔指数是衡量个人或地区间收入差距的指标,泰尔指数越高表示越不公平,取值为0~1,一般认为泰尔指数值大于0.4,则存在较大的不公平,其计算公式为:

其中,T为泰尔指数;x表示的是泰尔指数以x为权重进行计算,y是指对公平性度量对象的测量指标。
5 集中指数法
集中指数法:集中指数方法一般用于公共卫生系统测度健康不平等,世界银行推荐使用集中指数法用于测量不同社会经济条件下卫生服务体系的公平性,本文将其引入农村基础设施投资公平性研究的领域中,利用该方法测量不同经济水平( 以地域分布作为衡量标准) 地区农村基础设施投资的公平性。集中指数的计算公式为:

6 阿特金森指数法
阿特金森指数是测度收入分配不公平指数中明显带有社会福利规范看法一个指数。阿特金森指数首先计算出一个等价敏感平均收入yε(yε定义为如果每个人享受到了这样一个等价敏感收入时的社会总福利,相当于收入实际分布时具有的社会总福利值)。

其中 yi为第i人(或组)的实际收入(总收入);f(yi)为第i人(或组)占总人口比例的密度函数;ε为不平等厌恶参数。该参数反映社会对于不平等的厌恶(或对平等的偏好) 程度,其取值范围是0<ε<+∞随着ε的增加,社会给予更大的权重给收入相对较低的人群。比较典型的ε权重有0.5和2。在定义了yε后阿特金森指数可以表示为:

其中μ为平均收入,从该指数可以看出:社会收入分配越公平,则yε越接近μ,阿特金森指数值也就越小;对于任何分布而言,阿特金森指数值的取值范围为[0,1],其中0代表社会达到了收入的完全公平分配;如果yi代表的是第i人的收入,则第i人占总人口数的比例就是1/n,
在上述六种衡量不公平程度的方法中,极差只利用了样本中的两个极端值,并不是样本整体数据离散程度的全面真实反映,而且易受通货膨胀因素的影响,因而,极差并不是一个很好的统计指标。基尼系数法的应用虽然是首选, 但是在具体计算基尼系数时可能存在计算复杂等问题,庞大的运算量会使得在计算过程中出现很多失误,影响计算结果。阿特金森指数与其他测量贫富差距的指标最大的区别就在通过不平等厌恶指数表示不同收入群体对差距的容忍度,有助于解释不同国家(地 区)的不平等对经济发展或社会稳定的影响。但其主观性和变动性较强,不同学者计算出来数值可能不一致,不利于比较分析。

