拉格朗日乘数法求解条件极值问题
罗 棋,朱珊珊
(吉林师范大学 数学学院,吉林 长春 130000)
引言
多元函数的条件极值[1]275-276问题常用拉格朗日乘数法进行求解,而泛函的条件极值[2]19-20问题的解法是关于多元函数条件极值的拉格朗日乘数法的直接推广.条件极值在实际问题中有着广泛的应用,本文讨论最常用的拉格朗日乘数法对多元函数的条件极值问题和泛函的条件极值问题进行求解和应用.
1 条件极值问题
1.1 多元函数的条件极值问题
多元函数的条件极值问题的一般形式是在条件组
φk(x1,x2,…,xn)=0,k=1, 2,…,m(m (1) 的限制下,求目标函数 y=f(x1,x2,…,xn) (2) 的极值. 泛函[3]64-65的条件极值问题的一般形式是在约束条件 (3) 之下,求 (4) 的极值.其中,G是m(m (5) 式(1)和(2)所表示的一般条件极值问题的拉格朗日函数是 L(x1,x2,…,xn,λ1,λ2,…,λm) (6) 其中,λ1,λ2,…,λm为拉格朗日乘数 的解. 引入待定的向量函数 λ(t)=(λ1(t),…,λm(t))T (7) 作辅助函数[5]193-196 (8) 如果条件泛函极值问题式(4)和(3)在x(t)=(x1(t),…,xn(t))T∈Ω达到极值,则必存在函数λ(t)=(λ1(t),…,λm(t))T使得x(t)=(x1(t),…,xn(t))T满足欧拉方程组 (9) 由欧拉方程(9)和约束条件(3),可解出泛函条件极值问题的极值曲线x(t)和拉格朗日乘子函数λ(t). 例1抛物面x2+y2=z被平面x+y+z=1截成一个椭圆.求这个椭圆到原点的最长与最短距离. 解这个问题实质上是要求函数f(x,y,z)=x2+y2+z2在条件x2+y2-z=0 及x+y+z-1=0下的最大、最小值问题. 令L(x,y,z,λ1,λ2)=x2+y2+z2+λ1(x2+y2-z)+λ2(x+y+z-1) 对L求一阶偏导数,并令它们都等于0,则有: 求得这方程组的解为: 解引入拉格朗日乘子λ(t),构造新的泛函 欧拉方程为: 2u-λ=0 将边界条件代入上式,有: 求解得: 于是,所求的函数和极小值曲线分别为: 在求解有约束条件的多元函数极值时,应用拉格朗日乘数法是一个非常好的办法,并且可将拉格朗日乘数法进行变形推广到求解泛函的条件极值问题,本文对这一方法进行探讨,并进行了实际应用.1.2 泛函的条件极值问题

2 拉格朗日乘数法求解条件极值
2.1 拉格朗日乘数法求解多元函数条件极值

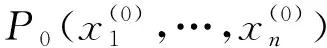

2.2 拉格朗日乘数法求解泛函条件极值
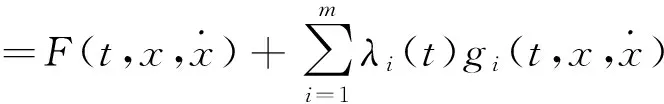


3 拉格朗日乘数法求解条件极值的应用
3.1 拉格朗日乘数法求解多元函数条件极值的应用
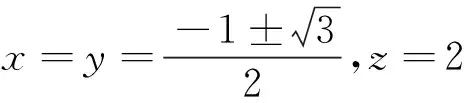

3.2 拉格朗日乘数法求解泛函条件极值的应用
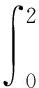
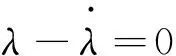
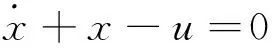
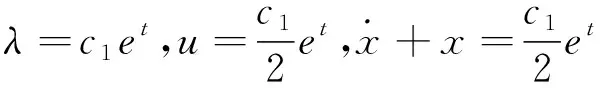
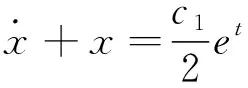
4 结语

