Improved GNSS Cooperation Positioning Algorithm for Indoor Localization

TaoyunZhouBaowangLianSiqingYangYiZhangandYangyangLiu

Abstract: For situations such as indoor and underground parking lots in which satellite signals are obstructed, GNSS cooperative positioning can be used to achieve highprecision positioning with the assistance of cooperative nodes. Here we study the cooperative positioning of two static nodes, node 1 is placed on the roof of the building and the satellite observation is ideal, node 2 is placed on the indoor windowsill where the occlusion situation is more serious, we mainly study how to locate node 2 with the assistance of node 1. Firstly, the two cooperative nodes are located with pseudo-range single point positioning, and the positioning performance of cooperative node is analyzed,therefore the information of pseudo-range and position of node 1 is obtained. Secondly,the distance between cooperative nodes is obtained by using the baseline method with double-difference carrier phase. Finally, the cooperative location algorithms are studied.The Extended Kalman Filtering (EKF), Unscented Kalman Filtering (UKF) and Particle Filtering (PF) are used to fuse the pseudo-range, ranging information and location information respectively. Due to the mutual influences among the cooperative nodes in cooperative positioning, the EKF, UKF and PF algorithms are improved by resetting the error covariance matrix of the cooperative nodes at each update time. Experimental results show that after being improved, the influence between the cooperative nodes becomes smaller, and the positioning performance of the nodes is better than before.

Keywords: Indoor localization, GNSS cooperative positioning, extended kalman filtering(EKF), unscented kalman filtering (UKF), particle filtering (PF).

1 Introduction

With the advantages of low cost, wide coverage, and high precision, Global Navigation Satellite System (GNSS) gradually integrates into human life. It is the most widely used navigation and positioning technology in many scenarios [Song and Lian (2015); Zhang,Lian and Yan (2016)]. GNSS positioning accuracy is high under no-occlusion environment. However, in a sheltered environment, such as indoors, urban canyons, or areas where trees are heavily shaded, the positioning performance is poor and sometimes even cannot perform positioning [Chang, Hou, Li et al. (2014); Chang, Hou, Zeng et al.(2014)]. For these reasons, many other technologies applied to different environments have been used for positioning, such as base station positioning, wireless sensor network(WSN) positioning and assisted GNSS (AGNSS) positioning and so on. Base station positioning [Zadeh, Schlegel and Macgregor (2012)], which is mainly applied to mobile phone users, has a wide coverage, but its positioning accuracy can only reach tens of meters in an ideal situation, and its application in indoor positioning is not good. WSN positioning [Lopes, Vieira, Rei et al. (2015)] is suitable for indoor positioning, however,it needs the assistance of anchor nodes to obtain the position of other unknown nodes in the entire network. Besides, the topology of nodes and the communication distance of wireless modules will affect the continuity of positioning. AGNSS positioning [Li, Liu,Qu et al. (2016)] is very important for the navigation and positioning of users under weak signals, but it requires the support of a network location server and needs additional costs for the enhancements of the satellite-based and road-based technology, and the positioning performance in indoors is also not good. With the continuous development of communication technologies, location information service network in the future must develop toward fusing multiple technologies, sharing multiple types of information, and adapting to multiple environments. Cooperative positioning technology will emerge from time to time [Vincent, Damien, Philibert et al. (2018)].

The cooperative positioning research group funded by European Space Agency (ESA)proposes Peer-to-Peer Cooperative Positioning (P2P-CP), which combines the advantages of GNSS positioning and WSN positioning, and proposes a new solution to the problem of poor GNSS positioning in shadowed environments [Zadeh, Schlegel, Macgregor et al.(2012)]. The receivers broadcast and share the positioning location through the communication modules and achieve positioning with data fusion algorithm. GNSS positioning method does not require the construction of a complex facility network in advance and need no3t any extra fees, it is suitable for positioning in a complex environment, so it has a very good prospect for the development of Cooperative Positioning (CP) [Ricardo and CiaránMc (2017)]. The cooperation in CP refers to the cooperation between the information captured by the GNSS receivers and the ranging information between the cooperative nodes. A CP system needs to be equipped with a GNSS receiver, a ranging module, and a communication module [Luís, Philippe and Urbano (2017)]. The communication module which functions as a communication link is used to broadcast the node position information and the captured satellite information; the distance measurement module is used to measure the distance between the cooperative nodes. The nodes in cooperative positioning are peer-to-peer, which means that no central node acts as a data processing center for all nodes, no other infrastructure and fixed structure are needed. The nodes are free and can be either static or motive.

The cooperative positioning was initially applied to the positioning of mobile robots and did not refer to satellite positioning [Xiao, Vincent and Wang (2016); Georges, Xiao and Wang (2016)]. Wymeersch et al. [Wymeersch, Lien and Win (2009)] study the cooperative positioning based on wireless networks and adopt Least Square (LS) for data fusion. However, the LS method requires the error to follow positive distribution, and the Non-Line of Sight (NLOS) distribution in the ranging process is uncertain, it is not suitable for the GNSS cooperative positioning. Caceres et al. [Caceres, Sottile, Garello et al. (2010)] study and compare the data fusion algorithms of cooperative positioning.Fritsche et al. [Fritsche and Klein (2010)] study the cooperative positioning of GPS and GSM with the nonlinear filtering algorithm on the mobile terminal. Penna et al. [Penna,Caceres and Wymeersch (2010)] study the Cramér-Rao Lower Bound (CLB) of cooperative positioning. Sottile et al. [Sottile, Wymeersch, Caceres et al. (2011)] adopt particle filtering to perform data fusion. The simulation results show that this algorithm is superior to the Kalman filtering algorithm. Morosi et al. [Morosi, Re and Martinelli(2013)] study the point-to-point cooperative positioning with the assistance of precise and coarse time respectively. Chang et al. [Chang, Hou, Li et al. (2014); Chang, Hou, Zeng et al. (2014)] review the cooperative positioning and propose a cooperative positioning node selection strategy. Tong et al. [Tong, Tian and Li (2016)] analyze the performance of dynamic cooperative positioning system based on particle filtering algorithm. Because of its own advantages and simplification of the hardware system, GNSS cooperation positioning is a positioning technology with a promising future. However, this technology is still in the experimental stage, and its development is restricted by many factors, so it faces relatively big challenges [Xu, Chen, Xu et al. (2017)].

Due to the mutual influences among the cooperative nodes in cooperative positioning, we mainly study the data fusion algorithm, and improve the traditional EKF, UKF and PF algorithms by resetting the error covariance matrix of the cooperative nodes at each update time. The rest of paper is organized as follows. In Section II, the basic principle of GNSS cooperative positioning is analyzed, a baseline method based on double difference carrier phase used to the distance measurement between cooperative nodes is proposed,the system state model and observation model based on location-time are built. In Section III, the traditional EKF, UKF and PF are analyzed respectively, due to the mutual influence of nodes in the cooperative positioning, a kind of improved algorithm is proposed by resetting the error covariance matrix at each update time and some simulation experiments are done. Finally, in Section IV, we conclude our work.

2 Basic principle of GNSS cooperative positioning

Fig. 1 depicts the model of GNSS cooperative positioning [Zadeh, Schlegel, Macgregor et al. (2012)]. The entire cooperative positioning process can be seen in Fig. 2, which is divided into three basic stages: Ranging, broadcasting and positioning. The first stage is ranging, in which each node measures the distance to all the neighbor nodes that can communicate with each other. The second stage is broadcasting, in which each node sends its own location information and the captured satellite information to all the neighbor nodes within the coverage of its own signals, and stores it in one-to-one correspondence with the ranging information, and afterwards, the receiver begins to capture satellites information quickly. The final stage is positioning, the receiver calculates its own position by fusing the pseudo-range information, ranging information and location information of neighbor nodes. The entire cooperative positioning process requires two kinds of pivotal measurement information: pseudo-range information and distance information between cooperative nodes.

Figure 1: Model of GNSS cooperative positioning

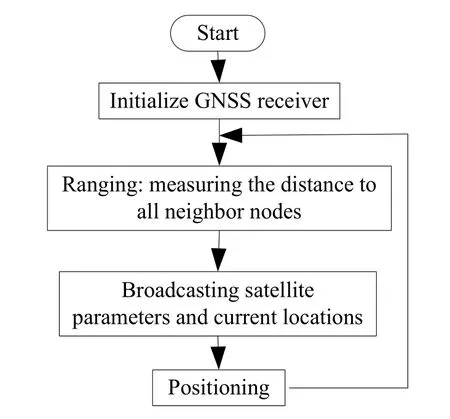
Figure 2: Flow diagram of cooperative positioning

2.1 Distance measurement between cooperative nodes based on double difference carrier phase

The measurement process of carrier phase can be described in Fig. 3.

Figure 3: Schematic diagram of carrier phase measurement

Certain satelliteSsends a carrier signal withphase atttime, after a while, attime,the receiverreceives the satellite signal withphase, then the phase changes during this time is

If the receiver clock error, satellite clock error, atmospheric delays and other errors are considered, the carrier phase observation equation can be described as:

2.2 Model of cooperative positioning

The main task of cooperative positioning is to find the state estimationof each cooperative node and its covariance matrixunder the condition that the location of visible satellite, pseudo-range measurementand its covariance matrix,location estimation of the peer cooperative node and its error covariance matrix,range measurements of cooperative nodesand its covariance matrixatttime are known. Here we mainly study the cooperative positioning based on two static nodes, one indoor and the other outdoor, so the location-time model is adopted.

2.2.1 System state model based on location-time

Let the state variable of each user node includes its three-dimensional positionunder the Cartesian coordinate system and the clock errorδtmwhich is usually expressed in the distance formbm=c⋅δtm, in other words, the system state variable is expressed as=, then the system state update model can be written as:

2.2.2 System observation model based on location-time

The measurement information of each node in cooperative positioning system includes the pseudo-range measurementsdistance measurementsobservation equation of nodeatttime can be described as:

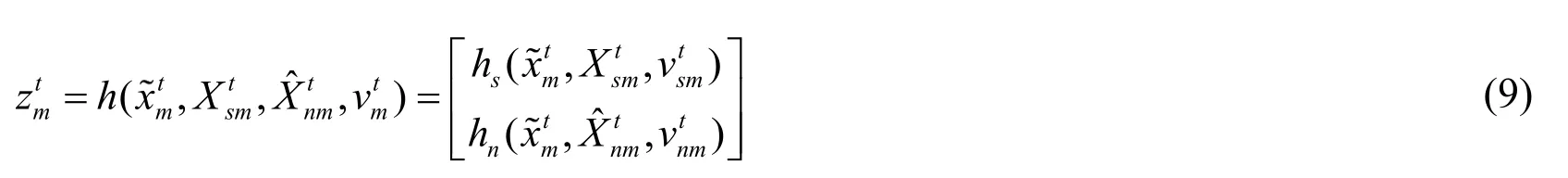
Measurement equation of pseudo-range can be written as:

Measurement equation of range between cooperative nodes can be written as:

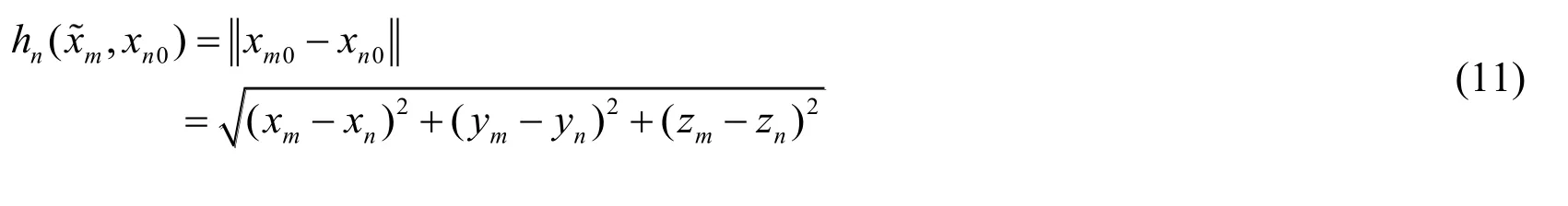
3 Algorithms of cooperative positioning

3.1 Traditional cooperative positioning algorithms

3.1.1 Extendted Kalman Filtering (EKF) algorithm

According to the priori state mean and its covariance, EKF can be used to estimate the linearization system and observation model, which can be divided into two processes:Prediction and correction.

(1) Prediction:

(2) Correction:

The priori state estimates obtained in the prediction phase are corrected with the actual measurements during the update phase.

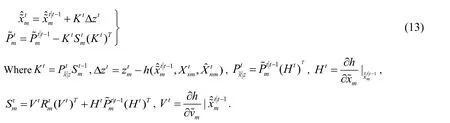
Algorithm flow of cooperative EKF is shown in Fig. 4.

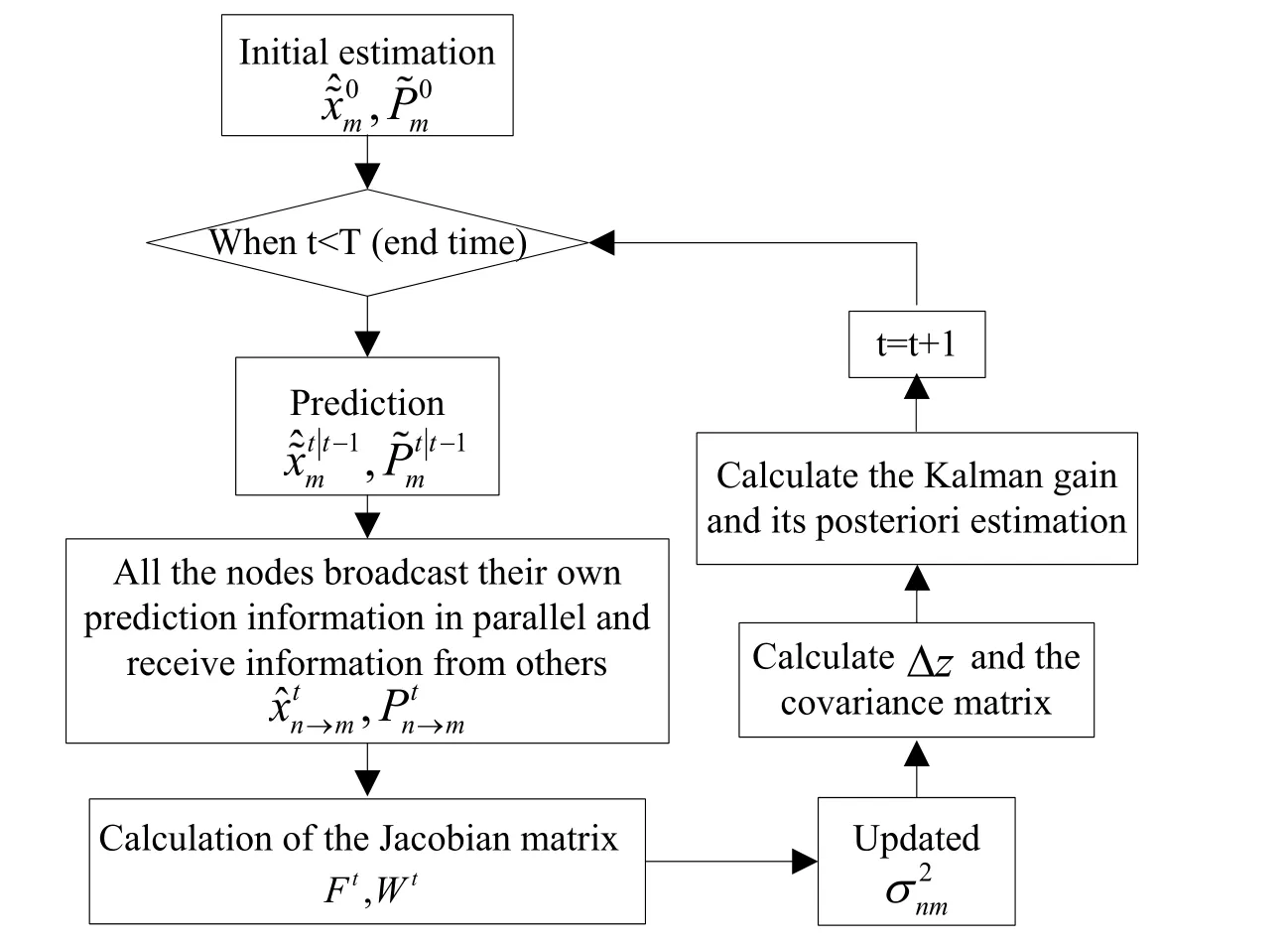
Figure 4: Algorithm flow of cooperative EKF

3.1.2 Unsented Kalman Filtering (UKF) algorithm

EKF can be used in nonlinear systems, but the negligence of higher order terms is prone to generate great errors and sometimes even cause filtering divergence. In order to solve the estimation problem under strong nonlinear conditions, UKF is proposed. The process of UKF is also divided into prediction and correction.

(1) Prediction:

The augmented state matrix added with process noise can be written as:

The priori state and its covariance matrix can be represented respectively as:

Where the weighted coefficientcan be calculated as follows:

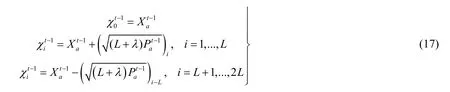
(2) Correction:

The augmented state added with measurement noise is:

The update of the state equation and its covariance matrix can be expressed as:

Algorithm flow of cooperative UKF is shown in Fig. 5.

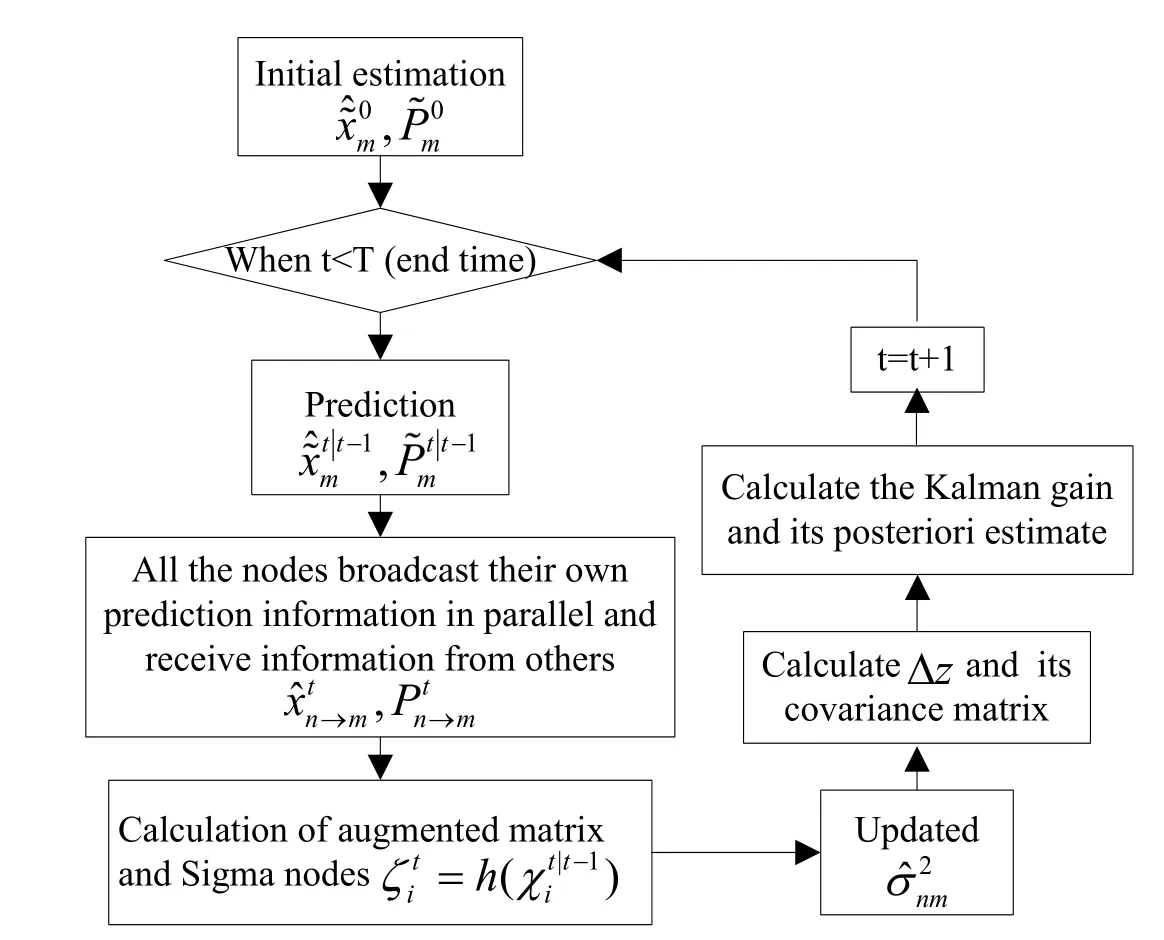
Figure 5: Algorithm flow of cooperative UKF

3.1.3 Particle Filtering (PF) algorithm

The process of PF is divided into prediction and correction too.

(1) Prediction:

Under the condition that posterior probability density functiontime is known, solve the prior probability density function attime through time update with the following:

(2) Correction:

Update the measurements attime based on Bayesian principle and calculate the posterior probability density function as:

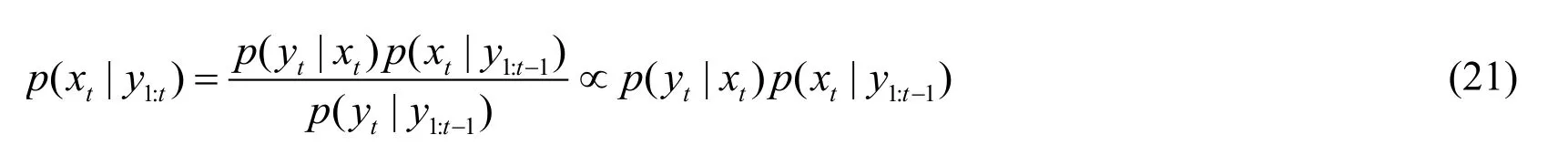
The probability distribution of discrete random samples constructed with particles and corresponding weights is represented as:

The posterior probability of particle estimation is calculated as:

Algorithm flow of cooperative PF is shown in Fig. 6.

Figure 6: Algorithm flow of cooperative PF

3.2 Improved cooperative positioning algorithm

In the process of cooperative positioning, the information exchanged between nodes includes position and distance, the positioning performance of EKF,UKF and PF will be affected by the uncertainty of the node itself and its neighbor nodes, and sometimes may even lead to filtering divergence. In order to solve these problems, firstly we regard the uncertainty of the node’s location estimation as a measurement with noise and establish a corresponding noise model, and secondly we assume that the peer nodes share the uncertainty in the form of state error covariance matrix and reset the error covariance matrix of the collaboration node at each update time.

3.2.1 The establishment of noise model

The uncertainty of the measurements is represented by measurement covariance matrixis the matrix which is related to the satellites, the propagation of satellite signals and GNSS receivers, andRnmis the matrix which is related to the ranging process between peer nodes. Here we consider the uncertainty of the node’s position estimation as a measurement with noise which may no longer be Gaussian distribution, so it is difficult to model the noise. Here we build the noise model by adding the original variance of measurements with the trace of the state error covariance matrix coming from cooperative nodes, the new variance can be described as:

3.2.2 Reset of error covariance matrix

Here we consider the cooperative positioning of two nodes, node1 placed outdoor is able to realize single-point positioning with a high positioning accuracy for it can acquire good satellite observations. However, due to the serious shelter, node 2 placed indoor needs the location information and its covariance matrix broadcasted by node 1 to assist its positioning. If the positioning error of node1increases, the trace ofwill increase significantly, leading todeviate from the real situation and result in a high positioning error for node 2 or even filtering divergence. In response to this phenomenon,we improve the traditional EKF, UKF and PF algorithms by resetting at each update time.

However, due to the state variables used in UKF is an augmented matrix,is reset toas:

3.3 Simulation analysis

3.3.1 Experimental environment

We study the indoor static cooperative positioning of two peer-to-peer nodes, node 1 and node 2 is placed on the roof and laboratory interior windowsill of the fifth-floor of the School of Electronics and Information, Northwestern Polytechnical University respectively. For node 1 is located in an open outdoor environment without obstructions,the observation condition is ideal, and the number of satellites that can be observed is large. The satellite observations at 3:00 to 7:00 on June 21, 2016 are shown in Fig. 7,where G, C and R represents the satellites of GPS, Beidou and GLONASS received by node 1 during this period respectively. It can be seen that during the entire observation period from 3:00 to 7:00, the number of observed GPS satellites and Beidou satellites are far more than four.

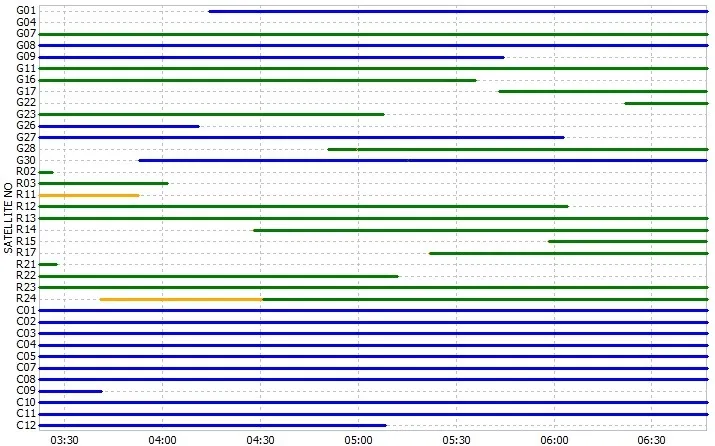
Figure 7: Satellite observations of node 1

Due to the obstruction of walls and poor observation conditions, the number of satellites that can be observed by node 2 is small, the observations at 3:00 to 7:00 on June 21, 2016 are shown in Fig. 8. It can be seen that the number of GPS satellites observed by node 2 during the entire observation period is less than 4, the number of Beidou satellites observed is slightly larger than that of GPS satellites, but most of the time is less than 5 and is not stability. Therefore, in such an occlusion environment, the reception of the receiver is not ideal, and a single GPS system even cannot be used for independent positioning.

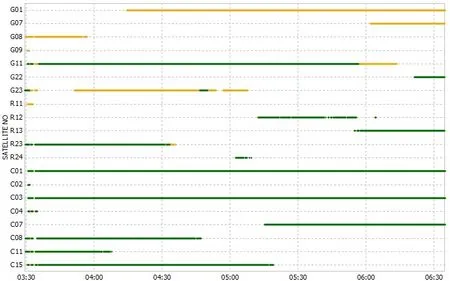
Figure 8: Satellite observations of node 2

Based on the observations of one whole week, we calculate theand earth rectangular coordinates of node 1, which is (34.03140320°, 108.76350725°,422.27646136m) and (-1702129.484m, 5010430.822m, 3549570.165m) respectively.Set its east-north-up (ENU) coordinates isA=(0, 0, 0). The GPS positioning of node 1 is shown in Fig. 9 and its directional errors in E, N, U are shown in Fig. 10.

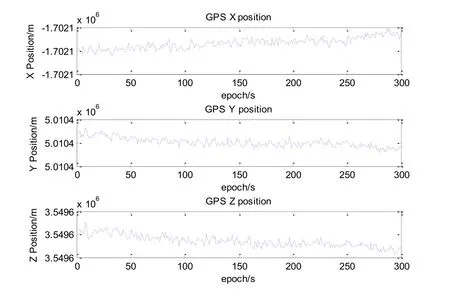
Figure 9: GPS positioning results of node 1 in earth rectangular coordinates system

The positioning RMS of Beidou and GPS of node 1 in the E, N and U directions is shown in Tab. 1, which depicts that the positioning error of node 1 in N direction during this period is greater than that in E and U directions for both GPS and Beidou, the positioning error of GPS is slightly smaller than that of Beidou, but the difference in positioning error is not large.

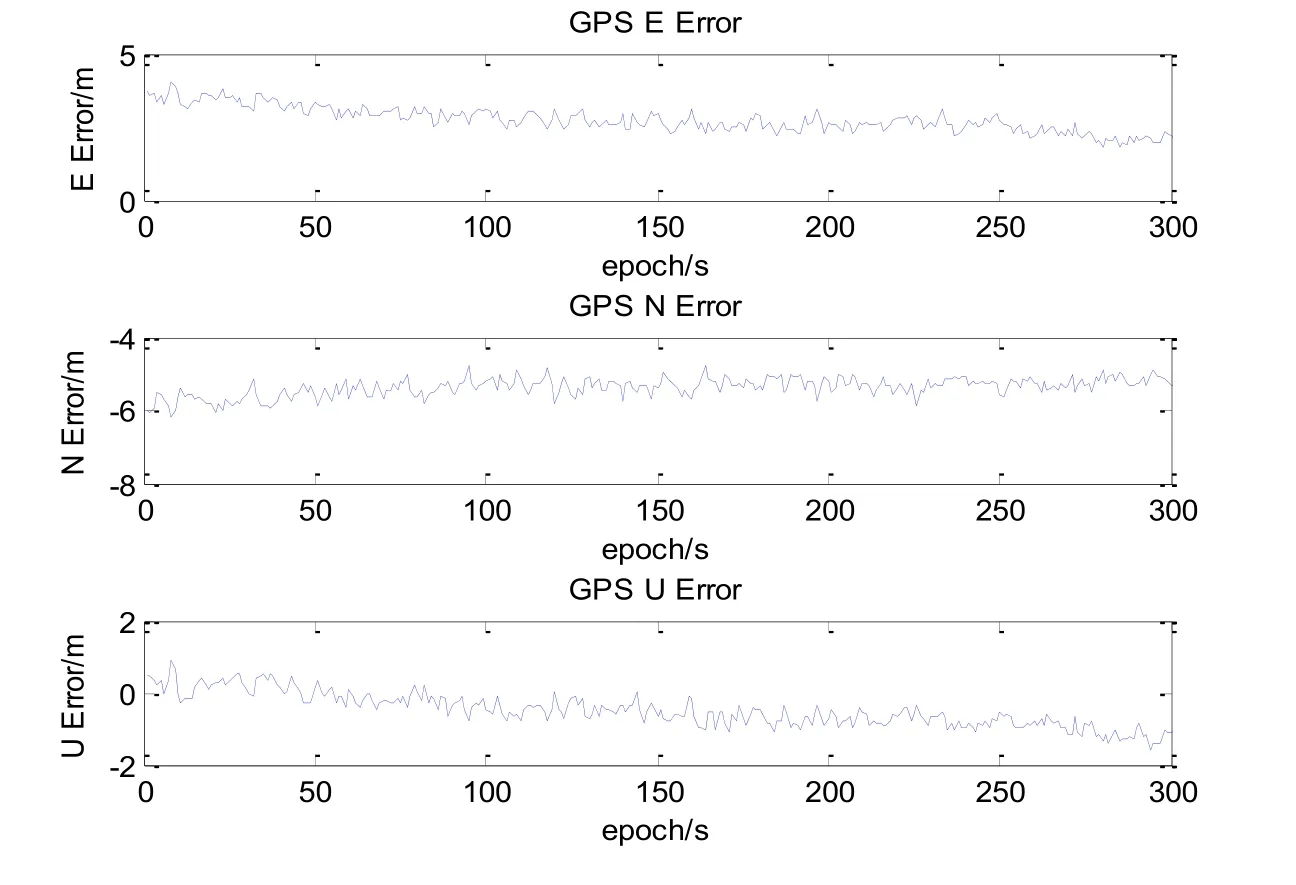
Figure 10: Directional errors of node 1 in the E, U and N directions

Table 1: Positioning RMS/m of Beidou and GPS of node 1 in the E, N and U directions

For the number of observed GPS satellites is less than four, Beidou pseudo-range positioning is used for node 2. Similarly, the 300 epochs of Beidou observation data began at 3:30:42 on June 21, 2016 is calculated for positioning. Calculate the average of the positioning results and we can calculate the rectangular coordinates of node 2 is (-1702120.2179m, 5010436.6589m, 3549572.7830m). For the precise position of node 2 is unknown in advance, the error analysis and comparison cannot be performed. The distance between node 1 and node 2 is calculated by solving the baseline with a doubledifference carrier phase method. Take node 1 as the origin, and solve the ENU coordinates of node 2 isB=(-5.1861m, -0.8038m, -3.9173m), the baseline distance between node 1 and node 2 is 6.5488m.

3.3.2 Simulation analysis of cooperative positioning algorithm

According to the satellite observations within 4 h from 3:00 to 7:00 on June 21, 2016, 50 epochs begun at 3:30:42 is selected for data analysis. Due to the obstruction of walls and poor observation conditions, the positioning accuracy of node 2 is low. Therefore, the information of distance between node 2 and node 1 and position of node 1 is used for cooperative positioning. LS algorithm, cooperative EKF, cooperative UKF and cooperative PF are used for simulation analysis. The positioning errors before and after improvement in X, Y, and Z directions are shown in Figs. 11-13 respectively.

Figure 11: Positioning error of X direction before and after improvement

Figure 12: Positioning error of Y direction before and after improvement

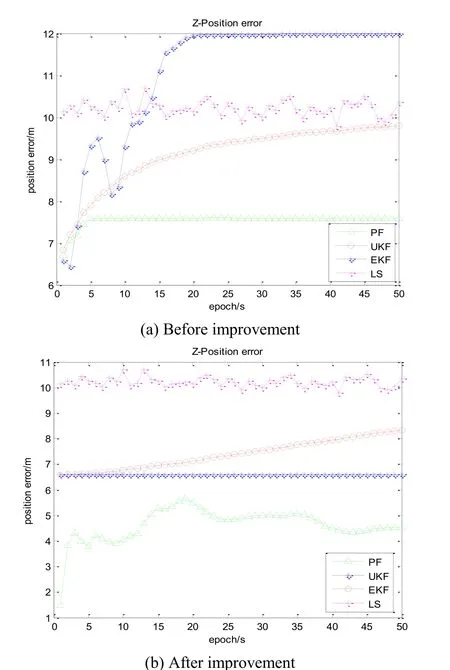
Figure 13: Positioning error of Y direction before and after improvement

Fig. 11 to Fig. 13 depict that the localization result curves of EKF are relatively smooth,due to the changes of the satellites number observed, there will be a relatively large curve jitter. Compared to EKF, the positioning result curves of UKF are smoother, and the positioning error is also smaller. Obviously, the positioning performance of UKF is better than that of EKF. Simulation results clearly show that the performance of PF is significantly better than that of EKF and UKF, but in terms of complexity, PF algorithm has the highest complexity and longest computation time. The statistical analysis of positioning error RMS of cooperative EKF, UKF and PF before and after improvement is shown in Tab. 2.

Table 2: Positioning error/m of node 1 with three algorithm before and after improvement in X, Y and Z directions

Tab. 2 depicts that the positioning error in Y direction is significantly higher than that in X and Z directions. The positioning error of the three improved algorithms is smaller than that before the improvement, so after being improved, the positioning accuracy of the cooperative EKF, UKF and PF is higher than that before being improved, which indicates that the improved algorithms are helpful for the improvement of the positioning accuracy and can be well applied to cooperative positioning.

4 Conclusion

In view of the problem of unsatisfactory satellite positioning in indoor and other sheltered environments, we study the cooperative positioning of two static nodes placed indoor and outdoor respectively. Firstly, single point positioning of GPS and Beidou is performed on the cooperative nodes respectively, and the positioning performance is analyzed and compared. Thus, the information of satellite pseudo-ranges and position of partial cooperative nodes is obtained. Secondly, the distance between the two cooperative nodes is obtained by using the baseline method of double-difference carrier phase. Finally, the EKF, UKF and PF algorithms are used to study the data fusion of pseudo-range, ranging information and location information. Due to the problem of mutual influences among the cooperative nodes in cooperative positioning, the EKF, UKF and PF algorithms are improved by resetting the error covariance matrix of the cooperative nodes at each update time. Experimental results show that the improved algorithms can reduce the mutual influences among nodes and improve the positioning accuracy greatly. However, we only study the cooperative positioning of two static nodes, we will study the dynamic cooperative positioning of multiple nodes in our next work.

Acknowledgement:This work was financially supported by National Major Special Science and Technology (No. GFZX0301040115), the National Natural Science Foundation of China (No. 61301094, No. 61571188), the Construct Program of the Key Discipline in Hunan Province, China, the Aid program for Science and Technology Innovative Research Team in Higher Educational Institute of Hunan Province, and the Planned Science and Technology Project of Loudi City, Hunan Province, China.