跳出传统假设检验方法的陷阱*——贝叶斯因子在心理学研究领域的应用

*

(1.浙江大学心理与行为科学系，杭州，310028；2.Department of Psychology,LMU Munich,Munich,80802,Germany)

1 引 言

在心理学以及众多社会科学的发展史上，假设检验作为一种简单易用的推论统计工具，长期为研究者们所青睐。几乎在每一篇心理学论文中，我们都能看到p值(往往是小于0.05，Fisher,1926)的存在。然而，由于假设检验方法本身存在一定的局限性，实际研究中经常会发生对p值意义的错误解读和假设检验方法的滥用，甚至有的研究者还会在研究中进行p值操纵(p-hacking)——即通过增减被试、变量或尝试不同的数据分析方法将p值控制在理想的范围。这会导致发表的论文中出现假阳性的结果，进而误导后续研究。近年来，很多科研工作者和科技论文期刊的编辑逐渐意识到假设检验的误用和滥用所带来的问题，并呼吁停止使用假设检验，更换其他统计方法。例如，美国的著名社会心理学期刊《基础与应用社会心理学》(BasicandAppliedSocialPsychology)在2015年称，虚无假设显著性检验(null hypothesis significance testing procedure,NHSTP)是无效的，并宣布禁止研究者在投稿中加入假设检验，包括p值、t值、F值等(Trafimow,2015)。无独有偶，2018年初美国政治学的顶级学术期刊——《政治分析》(PoliticalAnalysis)在社交网络的官方账号宣布，从2018年的第26期开始禁用p值(详见该期刊2018年第26期第1卷Comments from the New Editor)。根据该刊的声明，禁用p值主要原因是：“p值本身无法提供支持相关模式或假说之证据。”当然，该观点还有待商榷，但假设检验这一推论统计方法本身存在的问题却不容小觑。笔者将试图从假设检验的基本原理出发，为读者揭示心理学界目前面对的统计困境。

2 传统假设检验的问题

2.1 传统假设检验的基本原理

频率学派的假设检验主要是基于概率性质的反证法所实现的推论统计方法，即承认如下前提：小概率事件(发生概率小于0.05的事件)在单次抽样中不会发生。研究者先根据研究需要对总体做互斥的两种假设，即虚无假设H0和备择假设H1，选取合适的统计量，在假定虚无假设为真的情况下计算统计量及其对应的概率p。若p值小于预先确定的显著性水平α(一般将显著性水平α设定为0.05)，则说明观察到了小概率事件。由于小概率事件在单次试验中不会发生，因此认为虚无假设不成立，从而拒绝虚无假设，接受备择假设；若p值大于显著性水平α，则接受H0。

2.2 对传统假设检验的批评

尽管假设检验在心理学以及其他科研领域应用多年，但其存在的问题也在一定程度上制约了学术研究的发展，目前学界针对假设检验的批评主要包括以下三方面(Rouder,Speckman,Sun,Morey,& Iverson,2009;Wagenmakers et al.,2018a)：

2.2.1 假设检验的结果不直观

假设检验所得到的p值表示的是当虚无假设H0为真时，在多次重复试验中观测到与当前样本数据D一致或更极端数据的概率。简言之，p值是关于数据D在假设H0下的条件概率，即P(D|H0)，并非在观察到当前样本数据的前提下理论假设H0成立的后验概率P(H0|D)。在概率论上，P(D|H0)并不等同于P(H0|D)，而后验概率P(H0|D)才是判断虚无假设H0概率大小的依据。然而，在实际研究中研究者们通常会以P(D|H0)的大小来决定是否拒绝一个理论假设，这在逻辑上显然存在问题，也容易导致人们对p值意义的误解。

2.2.2 假设检验无法为虚无假设的成立提供证据

通过假设检验的基本原理可知，当p值大于显著性水平α时，由于不满足小概率反证法的条件，这一结果不能直接作为支持虚无假设H0成立的证据。虚无假设一般是假设研究的不同条件之间不存在差异，而备择假设一般是假设不同条件之间存在差异。由于大部分心理学研究都试图获得“显著效应”，因此研究者大多期待备择假设成立，即不同条件之间存在差异。然而，在心理学研究中并非只有差异性才具有学术价值和社会意义，比如证明不同群体(按不同性别、年龄、种族等变量分组)之间在认知功能上不存在差异有助于加深对其一般机制的理解，也可能有利于消除社会大众对特定群体的歧视。对于这类研究，传统的假设检验方法似乎无能为力。

2.2.3p值对样本容量的变化较敏感

众所周知，统计量(t、F等)会随着样本容量的增多变大，相应的p值也随样本容量的增多变小。即使在虚无假设为真的情况下，研究者仍可通过“p值操纵”推出p值小于0.05的假阳性结论：通过刻意扩大样本容量，并实时关注整体的p值变化，一旦到了显著性水平就停止增加被试量。这样的推论结果显然是毫无学术价值的。

假设检验的上述局限导致了研究者只能关注体现差异性的理论问题，而对涉及不变性或恒常性的理论问题束手无策，同时也给某些学术不当行为提供了野蛮生长的土壤。总而言之，心理学界迫切需要一种概念简单直观、能够为虚无假设提供支持且不受样本容量过多影响的统计方法，而贝叶斯因子(Bayes factor,BF)分析似乎是目前的一个合适选择。

3 贝叶斯因子

3.1 贝叶斯因子的意义

频率学派将随机事件发生的频率作为一种客观指标，而贝叶斯学派则从观察者的视角出发将概率理解为一种主观不确定性。在贝叶斯统计中，能够通过观察到的数据输出特定条件下对应的假设概率，这种量化后的数据结果可定义为后验概率，即P(H|D)。一种较合适的比较假设的方法即比较后验概率比，如以虚无假设H0和备择假设H1为例：

①

这里的后验概率比具有直接的意义：如果比值为20，那么在当前数据与已有先验预期下，备择假设成立的可能性是虚无假设的20倍。

另根据贝叶斯公式：

②

将包含H0和H1的②式各自代入①式中，消去P(D)可得：

③

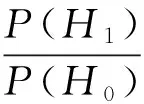
④

贝叶斯因子BF10表示H1和H0对比的贝叶斯因子，反之，BF01即为H0和H1对比的贝叶斯因子。

由上也可看出，贝叶斯因子不等同于后验概率，二者有不同的作用和含义。后验概率是根据已知数据来决定我们对某个事实的信念(belief)，并做出结论；贝叶斯因子则描述数据本身传递了多少证据(Etz & Vandekerckhove,2018)。

3.2 贝叶斯因子的优势

贝叶斯因子的概念最早提出于在20世纪60年代中期(Jeffreys,1961)。由于当时计算机运行速度有限，贝叶斯因子难以计算。近年来，计算机科学的飞速进步，使得贝叶斯因子的广泛应用成为可能。我们将贝叶斯因子的主要优势概括如下：

3.2.1 概念清晰，容易理解

根据上文给出的定义，若贝叶斯因子BF10=10，则说明在当前数据之下，备择假设成立的可能性是虚无假设的10倍；而BF10=0.1，即BF01=10，则表明在当前数据之下，虚无假设成立的可能性是备择假设的10倍。作为评估某理论成立可能性的指标，贝叶斯因子比p值更加直接和易于理解。

3.2.2 贝叶斯因子可以为虚无假设的成立提供证据

假设检验是先设定虚无假设，再以反证法检验备择假设，但难以证明虚无假设成立。贝叶斯因子分析对虚无假设和备择假设一视同仁，只是考察两者成立的可能性的高低，因此同样可以为虚无假设提供支持证据。后者适用于探究心理学领域的不变性、恒常性等问题。此外，由于贝叶斯因子作为虚无假设与备择假设两者成立概率的比值只是一种特例，因此它还适用于比较不同模型(或假设)对实验数据的解释程度。

3.2.3 对于大样本容量下的实验效应，贝叶斯因子比p值更加严格

图1是贝叶斯因子分析与虚无假设检验的临界t值随样本容量变化的曲线图。由图1可见，p值等于0.05对应的临界t

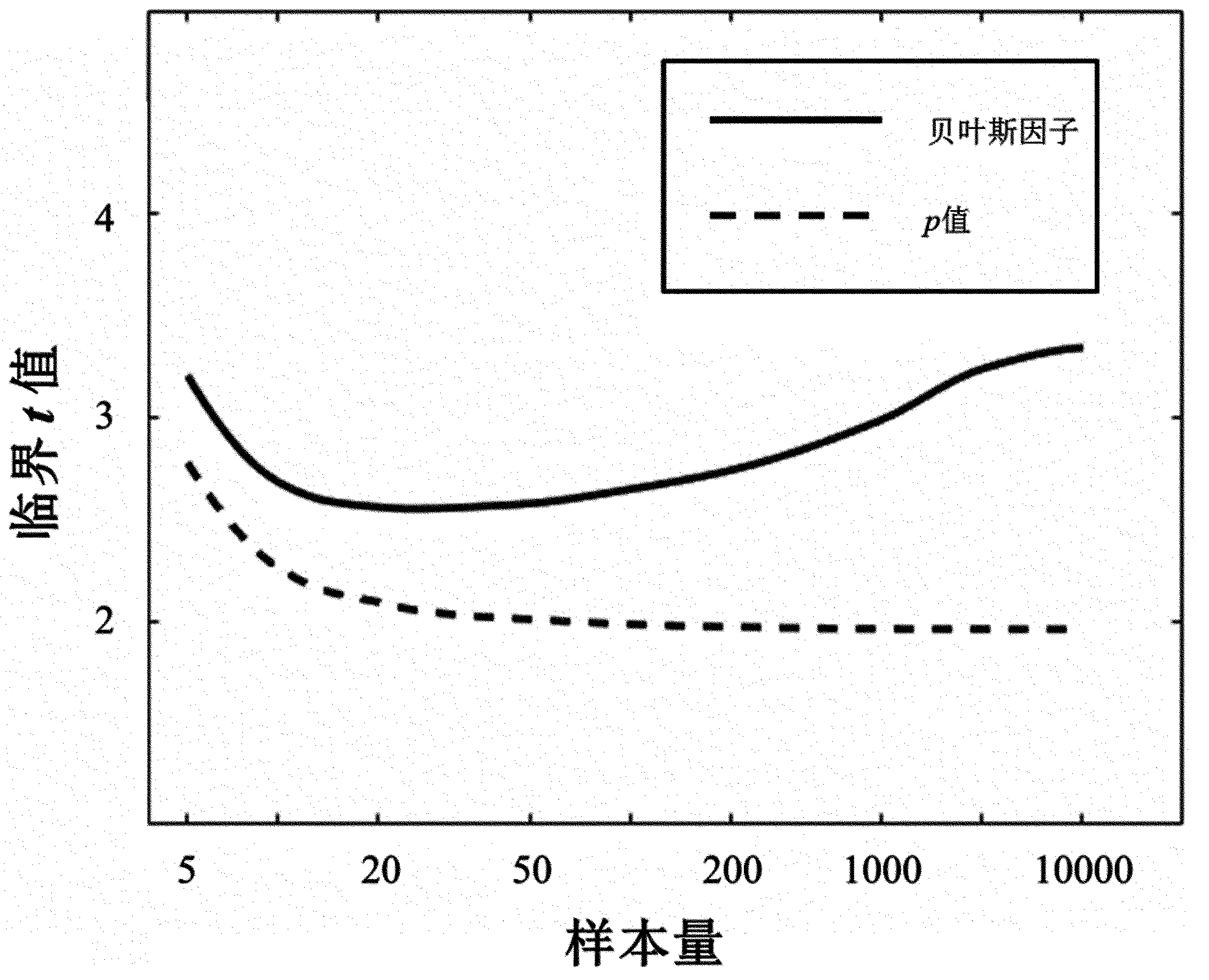
图1 贝叶斯因子分析与虚无假设检验的临界t值随样本容量变化曲线图

图中实线表示贝叶斯因子在备择假设成立可能性是虚无假设3倍的情况下对应的t值，虚线表示p值等于0.05的情况下对应的t值。

值小于贝叶斯因子等于3对应的临界t值，而且p值所对应的临界t值随着样本容量的提高而不断减小，而贝叶斯因子在达到一定的样本容量之后其临界t值反而随样本容量的提高而缓慢变大。因此，在某些情况下p值和贝叶斯因子对于同样的数据有可能得出完全不同的结论；贝叶斯因子分析方法也在一定程度上能够避免研究者不停收数据直到p值显著才停止的错误做法。

3.2.4 贝叶斯因子可以结合理论假设的先验概率与样本数据进行统计推断。

传统的假设检验并不考虑理论成立的先验概率，仅关注理论假设是否符合研究者当前收集到的数据。在贝叶斯因子分析中，我们可以结合前人的研究，整合先验信息与当前数据，并计算理论假设成立条件下的后验概率之比，从而判断当前证据的强度是否足够推翻(或支持)前人的理论。对于前人研究很少的效应，通常将虚无假设和备择假设的先验概率之比设置为1∶1；对于有充分证据支持的理论或者过于违背常识的假设，先验概率之比可以设置得相对悬殊些。例如，Bem在其2011年的一项研究中通过假设检验的统计方法发现，被试能够以显著高于随机水平的概率预知特定随机事件的发生，并进而讨论超感官知觉(extra sensory perception,ESP)存在的可能性(Bem,2011)。Rouder及同事用贝叶斯因子重新分析了Bem的数据，计算得出其贝叶斯因子BF10大约为40，即该效应存在的可能性是效应不存在可能性的40倍(Rouder & Morey,2011)。虽然其贝叶斯因子较高，但是由于超感官知觉本质上违背了因果律，也从未得到任何科学研究的支持，其先验概率显然应该远低于1/40，因此Bem的证据还不足以支持他的结论(Morey & Rouder,2011)。

3.3 评估贝叶斯因子大小的标准

贝叶斯因子分析能够帮助研究者根据现有证据评估不同假设成立的可能性之比，并且在评估证据强度上也有一套独立的标准(见表1)。

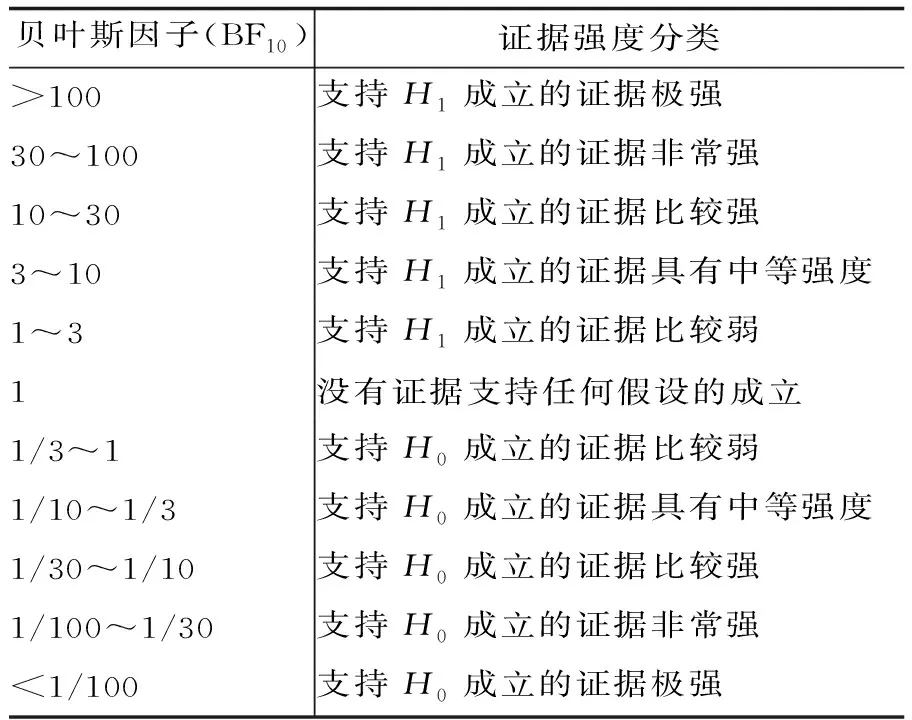
表1 贝叶斯因子BF10的不同数值对应的证据强度分类(调整自Jeffreys,1961;Wetzels & Wagenmakers,2012)

4 贝叶斯因子的计算

Jeffrey与Morey等在t检验的基础上，发展了针对多因素方差分析、多元回归分析的贝叶斯因子计算方法(如Rouder,Morey,Speckman,& Province,2012)。尽管贝叶斯因子在计算上相对复杂，但目前已经有多款软件支持贝叶斯因子的计算，如R语言中开发的BayesFactor软件包[注]BayesFactor软件包简介与获取详见http://cran.r-project.org/web/packages/BayesFactor/index.html、可视化统计软件JASP*

*JASP软件包简介与获取详见https://jasp-stats.org/等。这些软件满足了大部分心理学研究的统计需求。有关如何计算t检验、多因素方差分析的贝叶斯因子，以及如何应用贝叶斯因子进行统计推断，本部分将结合上述两款软件包进行简介。为使读者能精准理解相关操作，笔者在附录1、附录2中分别提供了两款软件包的具体操作示例(在《应用心理学》杂志在线下载)。

4.1 BayesFactor工具包的特点与注意事项

BayesFactor工具包由Richard D.Morey等人共同开发，是一款仍在实时更新的R语言工具包。它可用于计算各种简单实验设计下的贝叶斯因子，具体适用设计类型包括列联表、单样本或双样本t检验设计、单因素或多因素方差分析和线性回归模型。各常用设计的贝叶斯因子计算原理与过程已均有文章详细介绍，如t检验(Rouder et al.,2009；Morey & Rouder,2011),线性回归(Rouder & Morey,2012),方差分析(Rouder et al.,2012；Rouder,Engelhardt,McCabe,& Morey,2016；Rouder,Morey,Verhagen,Swagman,& Wagenmakers,2016；Wetzels,Grasman,& Wagenmakers,2012)等，本文不作赘述。笔者仅针对较为常用的模型与计算语句(如ttestBF，anovaBF等)提供输入、输出的操作示例(见附录1)[注]更为详细的从安装、载入工具包开始介绍的英文原版BayesFactor使用简可见https://cran.r-project.org/web/packages/BayesFactor/vignettes/manua.html。结合这些操作示例，笔者对BayesFactor工具包的特点与使用注意事项做如下概括：

(1)BayesFactor工具包通过调用特定函数语句，在原有R语言统计函数帮助下(可实现载入数据、初步分析数据内容、准确进行传统统计检验),进一步调节选用模型与参数，从而实现贝叶斯因子的计算与输出。尽管该工具包在使用时包含了明确的指令输入，但是它又同时包含了不透明、不易懂的默认参数设定，故会对初学者造成一定的使用困难。

(2)工具包受限于具体的输入方式与极为局限的交互界面。如用于计算的输入函数往往包含若干个默认的参数，而初学者可能会错过、忽视若干可选设置或必选设置。故笔者建议研究者在使用初期结合BayesFactor工具包内的函数说明手册，详细了解待使用功能的适用条件与待输入参数类型，避免未修改默认参数而导致输出并不适配当前分析条件的贝叶斯因子。

(3)特定实验设计下导入的原始数据格式，与传统统计检验用的数据格式有较大的差别。以重复测量方差分析为例，在以往的SPSS检验中，每一列均可为一种特定而具体的实验条件，每一行为一次观测或若干次观测后平均的测量结果，并适当添加特殊列作为被试间分组变量。而在BayesFactor的数据导入中，默认的数据格式为每一列为特定的指标类型(如自变量和因变量)，每一行则为相应的自变量与因变量具体水平，其中自变量的命名需要为字符串格式以区分条件间异同，如包含被试间条件，则需要单独一列以字符串格式保留的被试编号，才能有效区分与识别是否为同一名被试在不同观测条件下的测量结果。在输入每一条包含特定标题行变量的函数语句时，需要确保每一个变量名都与待分析数据的抬头名严格一致才能有效运行特定函数语句。

(4)区别于传统统计检验(如方差分析)，给定实验条件与数据结果的贝叶斯因子并不是一个稳定值，而是一个区间，且每一次计算得到的结果区间间存在一定的波动。这与贝叶斯因子计算过程中的蒙特卡洛模拟过程相关。为避免误差较大时，挑选特定的贝叶斯因子结果进行选择性报告，Morey建议在报告时提供当次的误差范围[注]Morey,R.D.对此给出的回复http://forum.cogsci.nl/index.php?p=/discussion/3259/how-to-report-the-results-of-anovabf，或结合JASP软件等同时报告顺序检验(sequential analysis)等可支持贝叶斯因子稳定性的结果。

4.2 JASP软件的特点

JASP是一个免费开源、具有图形操作界面的统计分析软件。相比于BayesFactor工具包而言，这是一个功能更全面、操作更友好、对熟悉使用SPSS软件的研究人员更易上手的软件。其底层基于BayesFactor工具包。除传统的统计检验功能外，它还能实现诸如探索性因素分析、主成分分析、结构方程模型等功能。本文则注重于其现阶段能实现的贝叶斯因子计算功能，例如t检验(独立、配对、单样本)、相关分析(皮尔逊、斯皮尔曼和肯德尔相关)、一致性检验、方差分析(单因素，协方差，重复测量)、线性回归(也包括对数线性回归)、列量表、二项分布和元分析。在附录2中将分别提供使用JASP软件进行独立样本t检验和重复测量方差分析的贝叶斯因子计算操作过程。结合这两个操作示例，笔者对JASP软件计算贝叶斯因子的特点与使用注意事项做如下概括：

(1)JASP软件整体界面设计较为简洁明快，导入数据后使用者根据待分析数据结构进行相应的功能选择，相关的功能与布局较符合多数研究者的已有习惯。在计算贝叶斯因子的同时，也可进行传统的统计检验，输出结果是可直接使用的三线表。

(2)JASP的结果呈现全面、规范，研究者可根据需要选择所需的分析内容，甚至可直接将相关的分析图表用于科研论文中。

(3)JASP的分析功能亦具有一定的不透明性。如若缺乏对JASP中各个功能标签的深入理解，使用者易错过当前使用界面未提供但更合适的分析方式。因此，在不确定每一个标签或参数是否选择了最合适的选项时，笔者建议结合不同分析软件比较细微的功能定位差异以增进理解，或通过相关论坛网站进行具体条目的交流与讨论。*

*较有代表性的JASP & BayesFactor讨论论坛地址：http://forum.cogsci.nl/index.php?p=/categories/jasp-bayesfactor

5 贝叶斯因子应用于心理学研究的注意事项

尽管贝叶斯因子相比传统假设检验有着多方面的优势和便利，但贝叶斯因子并不是“万金油”，也和假设检验一样存在着难以在统计学框架下解决的问题。在将其应用于心理学研究之前，我们还需要了解以下几点注意事项：

5.1 贝叶斯因子的数值是相对的，而不是绝对的

这一点在多元回归分析等统计建模中尤其值得关注。比如BF12=100表示的是模型1成立的概率是模型2成立概率的100倍，但这并不能保证模型1就能很好地拟合数据，有可能两个模型对数据的拟合效果都很差，只是模型2比模型1更差而已。

5.2 贝叶斯因子比p值更加严格，但仍然可能被操纵

盲目扩大样本容量、选择性报告、随意剔除极端值都会影响贝叶斯因子的大小，从而导致与p值操纵类似的所谓的“B值操纵”。

5.3 贝叶斯因子无法根本性解决“发表偏倚”(publication bias)的问题

“发表偏倚”是指在同类研究中，达到统计显著性(如p<0.05)的研究结果更容易被学术期刊发表的现象，这很容易对其他研究者产生误导。上文提到过贝叶斯因子的评估标准，建立这一标准的主要目的是为了客观地评估证据的强度，但如果这套标准(比如BF>3)和p<0.05同样被奉为决定一篇文章能否发表的金科玉律，那么摒弃p值而采用贝叶斯因子只不过是“换汤不换药”而已。所以在如何合理运用贝叶斯因子的评估标准，以及如何在使用贝叶斯因子的过程中避免发表偏倚这些问题上，还需要学界从统计学和心理学之外的角度进行讨论和改善。

6 小 结

贝叶斯因子较传统统计方法有很多优势，其中最突出的优势是对虚无假设和备择假设一视同仁。这一方面能够帮助研究者解决为虚无假设提供证据的问题，另一方面还能帮助研究者拓宽思路，使更多心理学热点问题得到严谨的回答。此外，支持贝叶斯因子计算的统计软件正在逐渐增多，贝叶斯因子分析本身也在不断发展进步，这些都为贝叶斯因子分析在心理学研究领域的广泛应用提供了条件。