纸瓦楞管的轴向准静态缓冲吸能特性研究
康健芬 郭彦峰 付云岗 李 琼 吕亚博


摘 要:对4种正多边形纸瓦楞管进行了轴向准静态压缩实验,计算出缓冲吸能特性参数,分析了管方向、横截面形状、管长、压缩速率对纸瓦楞管的失效模式与缓冲吸能特性的影响。结果发现,X向纸瓦楞管仅发生手风琴变形模式,而Y向纸瓦楞管发生稳态渐进屈曲、欧拉失稳、角撕裂、横向剪切4种变形模式。对于Y向纸瓦楞管,正多边形横截面边数的变化对纸瓦楞管的缓冲吸能特性影响明显,压缩速率为12 mm/min和48 mm/min时,正三边形管和正五边形管的比吸能和单位面积吸能较高;当管长为150 mm或压缩速率为72 mm/min时,均会导致Y向纸瓦楞管的非理想变形模式占比增大,缓冲吸能特性降低。X向纸瓦楞管的变形模式更稳定可控,而Y向纸瓦楞管的缓冲吸能特性更优良。
关键词:纸瓦楞管;轴向准静态压缩;变形;缓冲吸能
中图分类号:TS76;TB332
文献标识码:A
DOI:10.11981/j.issn.1000-6842.2018.04.23
纸瓦楞是瓦楞夹芯结构被推广应用于包装科技领域而出现的一类非金属多孔夹层结构和材料,具有质量轻、比刚度/强度大、抗冲击性能高、成本低、工艺简单等优点,在军工/民用产品防护与包装工程领域都有很重要的应用价值,还可代替传统的木质材料及其包装[1-3]。在产品包装防护系统中,纸瓦楞作为缓冲吸能结构,被合理地放置于包装箱和产品之间,通过自身的压缩变形与缓冲吸能作用来实现产品保护与安全运输[2,4]。
典型的纸瓦楞能量吸收结构大致可划分为两大类:一类是层状结构形式(或层状纸瓦楞结构),如具有不同数量夹芯层的瓦楞纸板、折叠型和弹力型纸瓦楞结构、纸瓦楞与纸蜂窝或泡沫塑料的层合结构,利用横向压缩变形而实现缓冲吸能作用;另一类是管状结构形式(或管状纸瓦楞结构),如具有不同正多边形截面的纸瓦楞管、泡沫填充紙瓦楞管,通过轴向压缩变形而减缓外部载荷作用。有关层状纸瓦楞结构的承载性能和吸能特性方面的研究论文数量多、成果丰富。通过对单瓦楞、双瓦楞准静态和动态压缩实验,获得不同瓦楞的横向压缩力学性能、失效机理和能量吸收性能,结果表明瓦楞纸板逐层屈曲压溃,并提出了瓦楞参数、压缩速率对整体变形过程以及局部压溃的控制作用[5-8]。基于C型多层瓦楞纸板的缓冲特性和能量吸收图,采用中等应变率下评估动态应力的 Cowper-Symonds方程与实验数据,构建了一个综合考虑结构参数和应变率效应的多层瓦楞纸板的动态平台应力的预测方程[9-10]。通过研究X-PLY型瓦楞纸板、弹力型和折叠型纸瓦楞结构在不同高度下的跌落冲击动态响应和缓冲特性曲线发现,这些层状纸瓦楞结构具有优良的缓冲吸能特性[11-13]。利用虚拟质量方法,研究了多层瓦楞纸板、瓦楞纸板-泡沫塑料层合结构的跌落冲击响应、动态本构关系和缓冲性能优化方法,其计算结果与实验数据吻合较好,为这类结构的缓冲性能表征与工程运用提供了一种新思路[14]。
此外,管状纸瓦楞是一种非金属类缓冲吸能管状结构,在军工/民用产品防护与包装领域都有重要的工程应用价值,然而有关这类新型结构的缓冲吸能特性方面的研究成果几乎未见报道。近年来,研究者们利用瓦楞波形在轴向压缩条件下更易弯折变形的优势提出了金属或复合材料瓦楞管状结构,以有效改善薄壁管状结构的承载性能和能量吸收特性[2,15]。例如,Eyvazian等[16]研究了横向/纵向瓦楞铝合金圆管的几何参数对缓冲吸能特性的影响规律;结果表明,瓦楞管是提高传统金属圆管的轴向压溃模式的可控性和缓冲吸能机制的有效措施。Liu等[17]研究了正弦波形瓦楞铝圆管在轴向冲击载荷作用下的屈曲变形模式和能量吸收特性;解析和数值模拟结果表明,瓦楞圆管具有可控的、优异的缓冲吸能特性,冲击速度和瓦楞径厚比是控制轴向压缩变形的2个主要参数。张平等[18]利用塑性铰理论分析波纹金属管受轴向压缩时的吸能机理,推导出平均压溃载荷的解析公式,模拟研究了几何结构参数、材料性能参数和加载速度对波纹管吸能特性的影响规律。冯丽娜等[19]采用经典板壳屈曲理论分析了纵向和环向碳纤维复合材料波纹夹层圆柱壳的准静态轴压力学性能,获得了欧拉屈曲、整体屈曲、局部屈曲、面板压溃等4种失效模式下的极限载荷解析公式和失效机理图,结果表明,纵向波纹夹层圆柱壳的轴向承载能力及载荷/质量效率优于环向波纹夹层圆柱壳。Klaslan[20]对比研究了泡沫铝填充单/双瓦楞圆管结构在轴向动态压缩载荷作用下的抗压碎性能和能量吸收特性,指出泡沫铝填充瓦楞圆管的动态压缩变形曲线包含低初始峰值载荷和平滑的塑性平台区,是一种优异的缓冲吸能结构。
在受到轴向外力作用时,管状纸瓦楞结构能够通过自身的塑性变形来耗散外部冲击能量,对提高空投物资装备和产品包装运输的缓冲吸能特性都具有重要的学术意义和工程应用价值。本研究采用双瓦楞纸板,经过模切、压痕、粘接等工艺制成正多边形纸瓦楞管状结构,对比研究这类管状结构的轴向准静态压缩变形特性、失效模式,分析管方向、横截面形状、管长、压缩速率对承载能力和缓冲吸能特性的影响规律,为正多边形纸瓦楞管的研制与应用提供理论和技术基础。
1 轴向准静态压缩实验
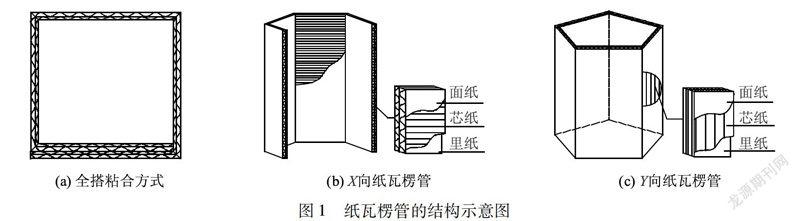
纸瓦楞管是由BC型瓦楞纸板经过模切、压痕、全搭粘合制成的正三边形、正四边形、正五边形、正六边形管状结构,其横截面边长为50 mm。BC型瓦楞纸板的基本参数如表1所示,纸板厚度7 mm,边压强度为6771 N/m。纸瓦楞管状结构的几何参数包括管方向、横截面形状、管长。对试件编号Cn-l-v-d,C代表瓦楞,n是横截面边数,l表示管长(70、110、150 mm,以110 mm为主),v是压缩速率(12、48、72 mm/min),d是瓦楞管的轴向(X、Y方向)。X向纸瓦楞管代表管轴向与瓦楞纸板的波纹方向(MD方向)平行,如图1(b)所示,Y向纸瓦楞管代表管轴向与瓦楞纸板的瓦楞方向(CD方向)平行,如图1(c)所示。例如“C5-110-12-X”表示横截面边长50 mm、管长110 mm的X向正五边形纸瓦楞管在压缩速率12 mm/min下轴向压缩。
实验前,所有试样按照国家标准GB/T 4857.2—2005“包装运输包装件温湿度调节处理”在温度20℃、相对湿度65%的环境条件下预处理24 h。每个纸瓦楞管的轴向准静态压缩实验参考国家标准GB/T 8168—2008“包装用缓冲材料静态压缩试验方法”,将试样放置在HT-2402电脑伺服控制材料试验机的下压板中央,上压板以恒定速率对纸瓦楞管沿轴向压缩,直到纸瓦楞管被压缩至密实化状态。
2 实验结果
2.1 压缩变形模式
(1)X向纸瓦楞管在轴向准静态压缩作用下只发生手风琴变形模式(见图2),因瓦楞芯层的正弦波纹的波峰和波谷是塑性铰的策源地,其具有良好的稳定性和可控性。在轴向压缩变形过程中,纸瓦楞管首先在底部或顶部出现一个折叠变形;随着变形量增大,纸瓦楞管沿着瓦楞波纹方向(MD方向)形成周期性的折叠单元;这种变形情况类似于弹簧压缩模式,当压缩载荷消除之后部分变形可恢复。
(2)Y向纸瓦楞管在轴向准静态压缩载荷作用下的变形模式包含稳态渐进屈曲、欧拉失稳、角撕裂、横向剪切,主要是稳态渐进屈曲与其余一种或多种非理想变形模式的混合,如图3所示。Y向纸瓦楞管在受到轴向压缩时,最先出现稳态渐进屈曲,由于芯纸和面纸排列方式的不同,导致芯纸与面纸分层变形,瓦楞芯纸沿着楞柱形成周期性折叠变形,面纸形成层状的折叠变形,如图3(a)所示。发生欧拉失稳的部分,只有弯折部分形成塑性铰,芯纸与面纸一致发生屈曲折叠;未弯折部分不发生变形且没有形成塑性铰,如图3(b)所示。随着横截面、管长或压缩速率的改变,会出现不同程度的角撕裂或横向剪切变形。沿棱线开裂的角撕裂,表面形成一条移形塑性铰外,其余不发生变化,如图3(c)所示,这种模式会使纸瓦楞管的承载力大幅减弱,总吸能和比吸能也降低。另外,横向剪切模式的发生是由于纸瓦楞管壁受到剪切力作用,双瓦楞纸板的面纸和芯纸发生脱层现象,面纸脱层后不发生周期性折叠压缩,但芯层沿瓦楞楞柱折叠压缩产生塑性铰,如图3(d)所示。
3 影响因素分析
3.1 管方向的影响分析
为了比较管方向对变形模式的影响,图4给出了X向和Y向正五边形纸瓦楞管的轴向压缩载荷-位移曲线以及不同时刻的变形情况比较。X向纸瓦楞管的塑性平台区比Y向纸瓦楞管的低很多,曲线波动幅值较大,出现较大波峰,对应着手风琴变形的塑性铰,I时刻达到初始载荷峰值,II时刻为平稳手风琴变形阶段,III时刻后开始进入密实化阶段。Y向纸瓦楞管在i时刻达到初始峰值载荷,ii时刻为稳态渐进屈曲变形阶段,iii时刻开始出现欧拉失稳和横向剪切,载荷值呈现下降趋势,能量吸收能力减弱。结合表2和表3所给出的缓冲吸能特性结果可知,Y向曲线波动比较细密且上下波动幅值较小,由于沿楞柱方向施加压缩载荷,其产生的抵抗力远远高于X向纸瓦楞管在楞波方向加载产生的抵抗力,总吸能、比吸能、单位面积吸能也均高于X向纸瓦楞管。X向纸瓦楞管的行程利用率基本在63%左右,压溃力效率在50%~85%之间;Y向纸瓦楞管的行程利用率在71%左右,压溃力效率高达70%~90%。
3.2 横截面形状的影响分析
不同横截面的X向纸瓦楞管的变形模式稳定,不随瓦楞管横截面形状的变化而变化。Y向纸瓦楞管的变形表现为多种模式的混合,随着横截面正多边形边数的增加,其变形更加复杂。正三边形纸瓦楞管主要发生稳态渐进屈曲和欧拉失稳的组合,正四边形纸瓦楞管主要发生稳态渐进屈曲、欧拉失稳和横向剪切的组合,正五边形纸瓦楞管和正六边形纸瓦楞管主要发生稳态渐进屈曲、欧拉失稳、角撕裂和横向剪切几种变形模式的组合,正六边形纸瓦楞管相比正五边形纸瓦楞管大部分发生了欧拉失稳和角撕裂,且角撕裂的程度更加严重。
管长110 mm的不同横截面纸瓦楞管在压缩速率12 mm/min下的载荷-位移曲线对比图如图5所示。结合表2和表3可得,由于正多边形横截面边数的增加导致纸瓦楞管的承压面积和总质量增加,X向与Y向纸瓦楞管的初始峰值载荷、平均压溃载荷、总吸能和行程利用率也逐渐增大。4种横截面形状Y向纸瓦楞管在不同压缩速率下的比吸能、单位面积吸能如图6所示。由图6可知,压缩速率为12 mm/min和48 mm/min时,正三边形、正五边形纸瓦楞管的比吸能和单位面积吸能都比正四边形、正六边形纸瓦楞管的高;压缩速率为72 mm/min时,由于压缩速率过高致使Y向纸瓦楞管的非理想变形占比增加,随横截面边数的增加,其比吸能和单位面积吸能下降。
3.3 管长的影响分析
为了评估管长对纸瓦楞管的影响,选用压缩速率12 mm/min的正五边形纸瓦楞管分析,其吸能特性参数值与轴向压缩载荷-位移曲线如表4与图7所示。X向与Y向正五边形纸瓦楞管在管长为110 mm时,初始峰值载荷、平均压溃载荷皆最高,管长过大反而引起承载力降低。由于纸瓦楞管的承载面积不变,管长的增加使得管的可压缩距离增加,X向纸瓦楞管与Y向纸瓦楞管的总吸能、单位面积吸能、行程利用率都增大,但由于结构总质量也增加,比吸能变化不大,管长为110 mm时纸瓦楞管的比吸能稍优。
对于Y向纸瓦楞管,试样C5-70-12的变形主要是稳态渐进屈曲,在临近底部出现了微小的欧拉失稳,也伴随着轻微的横向剪切现象;试样C5-110-12最先出现稳态渐进屈曲,再发生欧拉失稳、横向剪切,欧拉失稳比管长70 mm时严重;而试样C5-150-12的欧拉失稳最严重且出现了角撕裂现象,如图8所示。管长为150 mm时,纸瓦楞管出现的非理想变形模式占比增大,从而导致承载力下降,载荷-位移曲线有大幅度的下降趋势,故管长的增加致使Y向纸瓦楞管组合变形模式更加复杂,结构承载力降低。
3.4 压缩速率的影响分析
图9为X向与Y向正五边形纸瓦楞管3种压缩速率下的轴向压缩载荷-位移曲线比较,结合表2给出的X向纸瓦楞管的缓冲吸能特性结果可得出,由于变形模式的单一稳定,压缩速率的增大导致X向管结构的总吸能、比吸能和单位面积吸能都提高。对于Y向纸瓦楞管,稳态渐进屈曲的吸能相比欧拉失稳、角撕裂、横向剪切更稳定且吸能效率更好,为理想的吸能模式,压缩速率增大更易发生后三者变形模式。从图10对不同压缩速率下Y向纸瓦楞管的总吸能、比吸能、单位面积吸能和行程利用率的比較分析可知,随压缩速率的增大,正三边形和正四边形纸瓦楞管的总吸能、比吸能和单位面积吸能提高,其缓冲吸能特性提升;而正五边形和正六边形纸瓦楞管的总吸能、比吸能和单位面积吸能在压缩速率48 mm/min时最大,在压缩速率
72 mm/min时有所下降。这是由于压缩速率过高,导致正五边形和正六边形纸瓦楞管的非理想变形模式的占比增大,从而降低纸瓦楞管的能量吸收性能。Y向纸瓦楞管在压缩速率48 mm/min时的行程利用率最大;当压缩速率增加到72 mm/min时,由于组合变形模式的占比变化导致行程利用率降低,如图10(d)所示。
4 结 论
本实验研究了正多边形纸瓦楞管在轴向准静态压缩下的力学性能,计算出总吸能、比吸能、单位面积吸能、压溃力效率、行程利用率,分析了管方向、横截面形状、管长、压缩速率对纸瓦楞管的失效模式与缓冲吸能特性的影响。
4.1 X向纸瓦楞管只发生可控稳定的手风琴变形模式,而Y向纸瓦楞管有稳态渐进屈曲、欧拉失稳、角撕裂、横向剪切4种变形模式;几何参数和压缩速率对X向纸瓦楞管的手风琴变形模式几乎没有影响,但能影响Y向纸瓦楞管稳态渐进屈曲和3种非理想变形模式的占比。
4.2 压缩速率为12 mm/min和48 mm/min时,正三边形、正五边形Y向纸瓦楞管的缓冲吸能特性较优;正多边形横截面边数的增加使得两种方向纸瓦楞管的行程利用率提高,但Y向纸瓦楞管的行程利用率比对应横截面形状的X向纸瓦楞管高。对于3种管长和3种压缩速率下的Y向纸瓦楞管,当管长为150 mm或压缩速率为72 mm/min时都会导致其非理想变形模式占比增大,结构承载力降低,从而降低缓冲吸能特性。
4.3 由于Y向纸瓦楞管是沿芯纸楞柱加载,产生的承载力远大于沿X向纸瓦楞管的楞波方向加载产生的力,其总吸能、比吸能、单位面积吸能、压溃力效率、行程利用率都较X向纸瓦楞管高,故Y向纸瓦楞管作为缓冲吸能结构更具有优势。
参 考 文 献
[1] Jing Lin, Wang Zhihua, Zhao Longmao. Advances in studies of the mechanical performance of cellular metals and related sandwich structures[J]. Mechanics in Engineering, 2015, 37(1): 1.
敬 霖, 王志华, 赵隆茂. 多孔金属及其夹芯结构力学性能的研究进展[J]. 力学与实践, 2015, 37(1): 1.
[2] Lu Fude, Liu Jianxiong, Gao De. Review of constitutive model and its application of cellular cushioning material[J]. Journal of Zhejiang University (Engineering Science), 2014, 48(7): 1136.
卢富德, 刘雄建, 高 德. 多胞缓冲材料本构模型与应用进展[J]. 浙江大学学报(工学版), 2014, 48(7): 1136.
[3] Kooistra G W, Deshpande V, Wadley H N G. Hierarchical corrugated core sandwich panel concepts[J]. Journal of Applied Mechanics, 2007, 74(1): 259.
[4] E Yuping, Wang Zhiwei. Research progress in energy absorption characteristics of paper cushioning materials[J]. Journal of Vibration and Shock, 2010, 29(5): 40.
鄂玉萍, 王志偉. 纸质缓冲材料能量吸收特性研究进展[J]. 振动与冲击, 2010, 29(5): 40.
[5] Lu T J, Chen C, Zhu G. Compressive behavior of corrugated board panels[J]. Journal of Composite Materials, 2001, 35(23): 2098.
[6] Fu Yungang, Guo Yanfeng, Wang Zhongmin. Compression Deformation and Energy Absorption Properties of Corrugated Paperboard[J]. Transactions of China Pulp and Paper, 2015, 30(3): 31.
付云岗, 郭彦峰, 王忠民. 瓦楞纸板的压缩变形及吸能特性研究[J]. 中国造纸学报, 2015, 30(3): 31.
[7] Sek M, Rouillard V, Crawford S, et al. Enhancement of cushioning performance with paperboard crumple inserts[J]. Packaging Techno-logy & Science, 2005, 18(5): 273.
[8] Rouillard V, Sek M. Behaviour of multi-layered paperboard cushioning systems under impact loads[J]. Strain, 2007, 43(4): 345.
[9] Wang Dongmei. Cushioning properties of multi-layer corrugated sandwich structures[J]. Journal of Sandwich Structures & Materials, 2009, 11(1): 57.
[10] Wang Dongmei, Bai Ziyou, Gong Huxiang, et al. Dynamic proprty evaluation for a corrugated sandwich structure[J]. Journal of Vibration and Shock, 2014, 33(3): 94.
王冬梅, 柏子游, 龚户祥, 等. 瓦楞夹层结构动态力学性能评估[J]. 振动与冲击, 2014, 33(3): 94.
[11] Guo Yanfeng, Xu Wencai, Fu Yungang, et al. Dynamic shock cushioning characteristics and vibration transmissibility of X-PLY corrugated paperboard[J]. Shock and Vibration, 2011, 18(4): 525.
[12] Guo Yanfeng, Xu Wencai, Fu Yungang, et al. Comparison studies on dynamic packaging properties of corrugated paperboard pads[J]. Journal of Engineering, 2010, 2(5): 378.
[13] Guo Yanfeng, Becker W, Fu Yungang, et al. Package cushioning properties of corrugated paperboard pads with hollow pillars[C]// Proceedings of 2nd International Conference on Packaging Technology and Science, Wuxi, China, 2014.
[14] Lu Fude, Tao Weiming, Gao De. Impact response of series cushioning system and structure optimization analysis[J]. Journal of Zhejiang University (Engineering Science), 2012, 46(10): 1773.
卢富德, 陶伟明, 高 德. 串联缓冲系统冲击响应与结构优化分析[J]. 浙江大学学报(工学版), 2012, 46(10): 1773.
[15] Qiu Xinming, Pan Mingle, Yu Xiaohuan, et al. Analysis of the energy absorption properties for tubular structure under axial compression of different failure models[J]. Mechanics in Engineering, 2016, 38(5): 477.
邱信明, 潘明乐, 虞晓欢, 等. 不同失效模式下轴压管状结构的吸能特性比较[J]. 力学与实践, 2016, 38(5): 477.
[16] Eyvazian A, Habibi M K, Hamouda A M, et al. Axial crushing behavior and energy absorption efficiency of corrugated tubes[J]. Materials and Design, 2014, 54∶1028.
[17] Liu Zhifang, Hao Wenqian, Xie Jiamiao, et al. Axial-impact buckling modes and energy absorption properties of thin-walled corrugated tubes with sinusoidal patterns[J]. Thin-Walled Structures, 2015, 94: 410.
[18] Zhang Ping, Ma Jian, Na Jingxin. Theoretical study on the crash worthiness of corrugated tube[J]. Journal of Mechanical Strength, 2015, 37(4): 676.
张 平, 马 建, 那景新. 波纹管耐撞性的理论研究[J]. 机械强度, 2015, 37(4): 676.
[19] Feng Lina, Xiong Jian, Zheng Wei, et al. Fabrication and axial compression properties of composite corrugated sandwich cylindrical shells[J]. Acta Materiae Compositae Sinica, 2016, 33(2): 418.
冯丽娜, 熊 健, 郑 伟, 等. 复合材料波纹夹层圆柱壳设计及轴压性能[J]. 复合材料学报, 2016, 33(2): 418.
[20] Klaslan C. Numerical crushing analysis of aluminum foam-filled corrugated single-and double-circular tubes subjected to axial impact loading[J]. Thin-Walled Structures, 2015, 96: 82.
[21] Li Zhibin, Yu Jilin, Zheng Zhijun, et al. An experimental study on the crashworthiness of thin-walled tubes and their metallic foam-filled structures[J]. Journal of Experimental Mechanics, 2012, 27(1): 77.
李志斌, 虞吉林, 鄭志军, 等. 薄壁管及其泡沫金属填充结构耐撞性的实验研究[J]. 实验力学, 2012, 27(1): 77.

