基于波动量法的用户侧谐波发射水平评估方法研究
缪江豫


摘 要:电网中存在多种谐波,这些谐波成非线性。为了能将谐波源准确定位出来,本文主要从波动量法的基本原理出发,利用系统侧和用户侧输出的谐波对公共连接点造成的影响,准确辨识出谐波源的位置,从而对谐波的发射水平进行合理评估。通过仿真分析,验证波动量法的有效性。
关键词:谐波阻抗;谐波发射水平;波动量法;公共连接点
中图分类号:TM711 文献标识码:A 文章编号:1003-5168(2018)14-0056-03
Assessing the Harmonic Emission Level Based on Fluctuation
Method Methodological Research
MIAO Jiangyu
(Henan Zhonghui Electric Power Engineering Consulting Co., Ltd,Zhengzhou Henan 450000)
Abstract: There are many kinds of harmonics in the power grid, and these harmonics are nonlinear. In order to locate the harmonic source accurately, this paper, based on the basic principle of the wave method, used the influence of the harmonics output by the system side and the user side to the common connection point, and accurately identified the location of the harmonic source, so that the harmonic emission level was reasonably evaluated. The validity of the volatility method was verified by simulation analysis.
Keywords: harmonic impedance;harmonic emission level;fluctuation method;point of common coupling
1 研究背景
随着科技的不断进步,越来越多的电子产品被运用到电力网络中,而这些电气设备大多是非线性的,从而产生大量的谐波传送到电网中,主要包括一些大型的交流控制器、变压器和逆变器等非线性负载。而谐波产生的最根本原因是非线性负载。在电力网络中,当负载起动,电流经过这些负载时,电流与加载设备的电压产生不对称性,形成非线性的干扰,从而在电网中产生谐波[1]。
电弧设备由于工作特性,电弧在70V以上的条件下才会有弧电流产生,且灭弧电压略低于起弧电压,造成弧电流与弧电压的非线性。此外,弧电流的非对称性使其波形成为非正弦波,从而在电网中产生多次谐波,对电网造成非常大的谐波污染。
交流整流设备在电网中也会产生较多谐波,设备中的设置阀电压小于额定值时,产生的电流为零,这主要是因为产生谐波污染。为了补充系统中的电流,为其提供优质稳态的电源,在整流设备中加入了滤波电容和滤波电感,从而使阀电压提高,加激了谐波的产生量。为了使系统中的电压和电流值成一定的线性关系,在系统中加入了硅元素,这使得整个系统的污染更大。
基于上述问题,本文提出了一种基于波动量法的谐波源阻抗估计方法,并对用户的谐波发射水平进行评估。该方法能有效地对谐波源进行定位,并对谐波的治理提供了更好的方案。笔者通过仿真分析,验证了该方法的有效性。
2 波动量法
谐波波动量法的基本思想是:在配电系统中,电流的变化会引起电压的变化,从而干扰谐波阻抗。系统电压的变化量在电流变化量的对比下,可以估计出阻抗的上升曲线,从而稳定系统的工作状态。
为了便于对系统进行评估,将电网系统等效为诺顿等效电路[2-4],等值电路如图1所示。
[IS][ZS][PCC][VPCC][IPCC][ZC][IC]
图1 等值电路
图1中,IS为系统侧等值h次谐波电压源,IC为用户侧等值h次谐波电流源,ZS为系统侧等值h次谐波阻抗,ZC为用户侧等值h次谐波阻抗,PCC(Point of Common Coupling)为公共连接点,VPCC、IPCC为公共连接点的谐波电压和电流。
通过对电路图进行初步计算,可以得出系统的等效计算公式:
[Vpcc=Ipcc+IcZc] (1)
[Vpcc=Is-IpccZs] (2)
当系统工作一段时间,系统中的谐波电流会发生相应变化,其提升量为[ΔIs],从而可以估算出系统的额谐波电压的变化量[ΔVpcc-s],则式(1)变为:
[Vpcc+ΔVpcc-s=Ipcc+ΔIpcc-sZc+IcZc] (3)
式(3)減去(1)得:
[Zc=ΔVpcc-sΔIpcc-s] (4)
通过相同的计算方式,可以估算出用户侧电压的变化量[ΔVpcc-s],则式(2)变为:
[Vpcc+ΔVpcc-c=IsZs-Ipcc+ΔIpcc-cZs] (5)
式(5)减去(2)得:
[Zs=ΔVpcc-cΔIpcc-c] (6)
由上述几个公式得出额参数量,再根据[Zc]和[Zs]的特性可知,复阻抗的实部是大于零的,也就是[ReZk>0],[ReZs>0]。定义如下等式:
[Zk=ΔVpccΔIpcc] (7)
当[ReZk>0],[Ic]会发生变化,则[Zs]的估计值就是[Zk];当[ReZk<0],[Is]会发生变化,则[Zc]的估计值为[Zk]。
为了减少估计值[Zc]和[Zs]的误差,可以对多个[Zc]和[Zs]值进行取均值。谐波的发射水平可以估计出来。
[ΔVc=VpccZc-IpccZsZcZs+Zc] (8)
波动量法的理论原理比较简单,简化了对协同谐波源定位的模型,利用此方法可以较为简单地对谐波源的发射水平进行估计[5-9]。
3 仿真分析
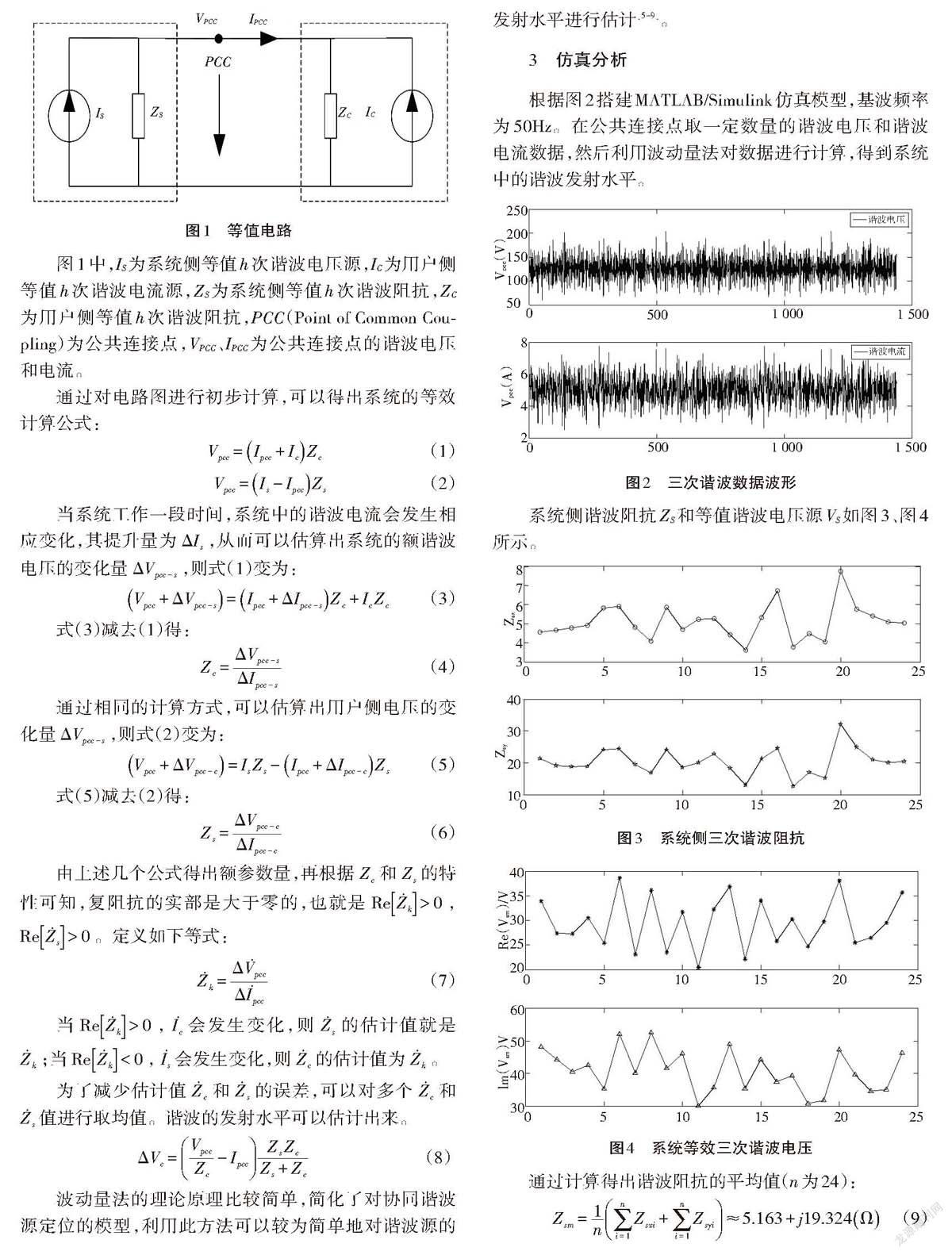
根据图2搭建MATLAB/Simulink仿真模型,基波频率为50Hz。在公共连接点取一定数量的谐波电压和谐波电流数据,然后利用波动量法对数据进行计算,得到系统中的谐波发射水平。
[Vpcc(V)][250
200
150
100
50][Vpcc(A)][0][8
6
4
2][500][1 000][1 500][谐波电流][谐波电压][1 500][1 000][500][0]
图2 三次谐波数据波形
系统侧谐波阻抗ZS和等值谐波电压源VS如图3、图4所示。

