基于混合连边机制的网络演化和渗流相变研究

王睿婕

摘 要：随机演化网络中的BFW渗流模型具有的强不连续相变以及多重巨型分支稳定共存的特性引起了统计物理学家的广泛关注。本文基于混合连边机制，提出了修改的BFW模型。大量模拟实验表明存在一个调控参数的临界点。当偏好连边概率大于该临界点时，生成网络的度分布呈现幂律分布；而小于临界点时，生成网络的度分布呈现泊松分布。进一步对该模型渗流特性的分析结果表明，当偏好概率大于临界点时，模型具有多级相变；而小于临界点时，只有一次相变发生。更有趣的是，当偏好概率小于临界点时，序参量在热力学极限下是自平均的。相反，序参量会出现随机震荡现象，且在热力学极限下不具有自平均性质。

关键词：随机网络；渗流；多级相变；自平均

中图分类号：N94；O357.3 文献标识码：A 文章编号：2096-4706（2018）02-0085-05

Research on Network Evolution and Seepage Transformation Based on Hybrid Connection Mechanism

WANG Ruijie

（ABA Teachers University，Aba 623002，China）

Abstract：The characteristics of the discontinuous percolation at the transition point and multiple giant components coexist in the supercritical region of the BFW model on random network has attracted much attention from physicists and statisticians. A modified BFW percolation model is proposed by changing the way of selecting the candidate edge. Through large numbers of numerical simulations，we find that there exists a critical point，which separates the type of the network structure. If the probability of the preferential attachment excesses the critical point，the network degree exhibits a power-law distribution. Otherwise，the network degree is poisson distribution. Additionally，the percolation process of the modified BFW model is researched. Simulation results indicate that the percolation undergoes multi-transition when the probability of the preferential attachment excesses the critical point. More interestingly，order parameter has random fluctuations when the probability of the preferential attachment excesses the critical point.

Keywords：random network；percolation；multiple-transition；self-averaging

0 引 言

渗流是统计物理学和概率论中被广泛研究的基本概念之一[1]，目前渗流模型被广泛应用于流行病传播[2]，网络信息传播与交互[3]，复合材料的电导[4]，生物蛋白质交互[5]，多孔介质[1]等领域中。

1959年至1961年间，Erd?s和Rényi提出了随机网络演化模型[6]，在该模型中，系统开始于N个独立的顶点，每次以完全随机的方式选取一条连边，并加入到系统中，其网络的渗流相变被认为是连续的二阶相变。

直到2009年，文献[7]对ER渗流模型随机连边规则稍作修改，引入竞争加边的乘积规则，延迟了最大分支的生长，导致网络序参量（系统最大连通分支的约化尺度）在相变点附近产生急剧变化，并称这种现象为“爆炸渗流”。

随后，大量相似或改进的添边规则被引入不同的网络结构中[8，9]并且同样得到了类似的爆炸渗流现象。特别地，文献[10]研究发现阿赫利过程下的序参量演化曲线具有随机震荡现象，而在ER随机演化模型中序参量在热力学极限下收敛到一条稳定曲线。此外陈巍等人研究了推广的BFW模型[11]，发现了多重巨型分支共存现象，并指出这种相变是强不连续的。

本文基于经典BFW模型，研究了在混合选边机制下，网络结构和渗流相变的变化情况，并提出了修改的BFW模型中的候选边的选取方式，并称之为修改的BFW（简记为MBFW）模型。数值模拟和理论分析表明存在一个生成网络结构类型变化的临界点γc，同时该临界点也是渗流是否具有多级相变的临界点。

此外，研究发现了更有趣的现象：实验表明，随着控制参量的变化，序参量的自收敛性在临界点γc处也随之发生改變。

1 模型介绍

为方便描述，记时刻t=l/N为当前添加到系统中的连边数与系统尺度比值。将BFW模型中候选边选取方式进行如下的修改：第一个结点按照随机的方式从系统中选取，第二个结点以概率γ按度大优先选取（每个顶点被选择的概率为该顶点的度数与当前系统中节点总度数的比值，，ki（t）为节点i在时刻t时的度数），否则以1-γ的概率从系统中随机选取。

连接这对顶点得到一条候选边eu，对得到的候选边eu按照BFW模型算法判断该条候选边是否添加到系统中，BFW算法描述见文献[11]。

2 网络结构分析

首先，假设每一条侯选边在每一步都被接受，即不受阶段数K和衰减函数g（K）的限制，称按照这种方式增长的网络模型为ER-like模型，在ER-like模型下每添加一条边，系统中每个顶点被选中的概率为：

（1）

（2）

（3）

为节点i被选中为主节点的概率，为节点i被选中为从节点的概率。我们将表达式（2）与文献[12]提出的幂指数可调模型中的优先连接机制相联系，在Price模型中，每个已经存在的节点被新添加边指向的概率为：

（4）

（4）式可以理解为：1）以概率p按照度大优先选择，每个节点被选中的概率为，其中p∈（0，1）为可调节参数；2）以概率1-p按照完全随机地方式选取已有节点，此时每个节点被选中的概率为1/N，Nt为当前时刻添加到网络中的节点数。通过主方程方法可以计算出，其中α为可调节参数，为第i个节点的入度，λ=2+α/m，m为每次添边数，λ∈（2，∞）。如果把Price模型中的每一条有向边改为无向边，可得pk～（k-m+α）-λ，其中λ=2+α/m，且λ∈（2，∞）。

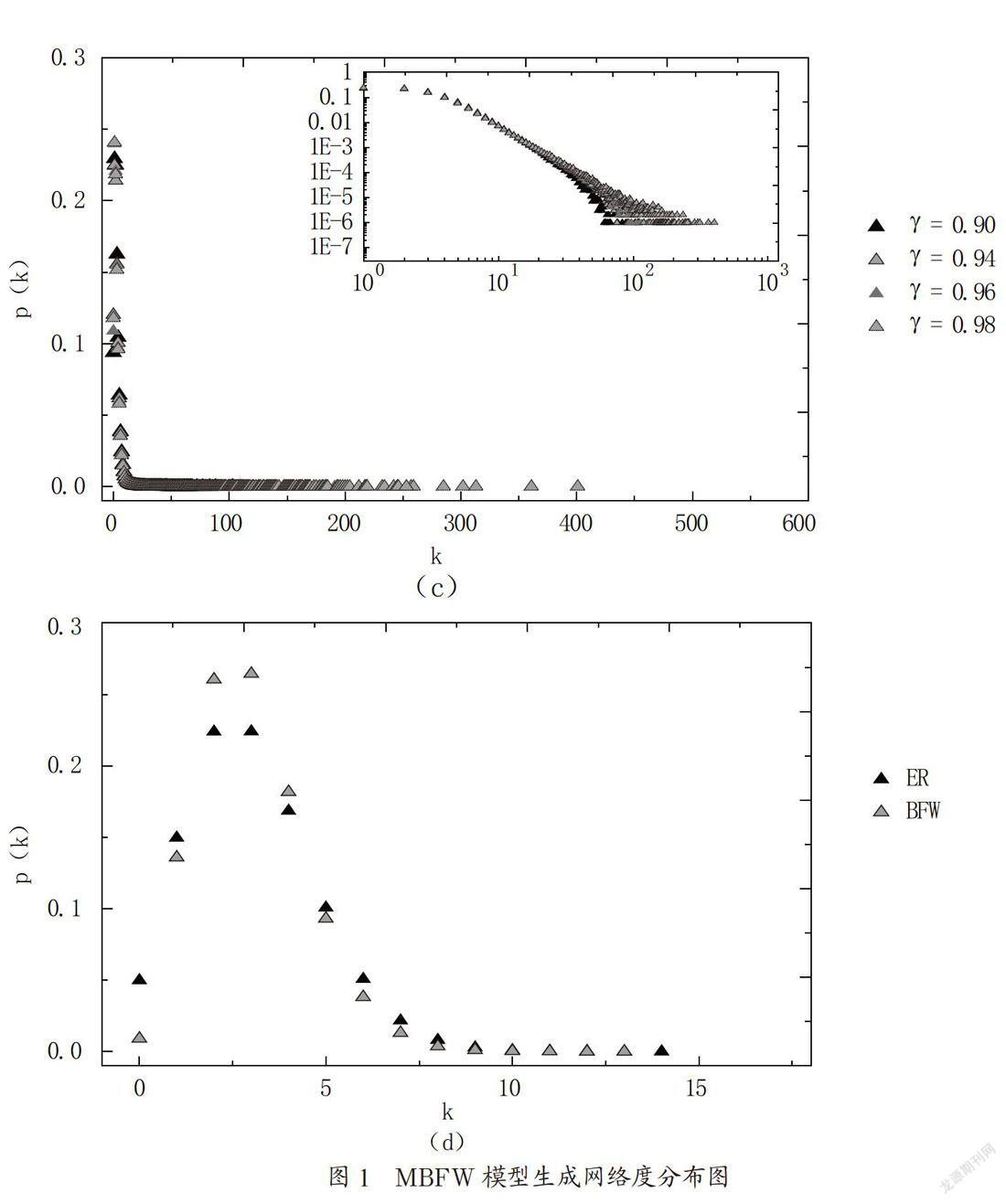
图1所示为MBFW模型生成网络度分布，系统尺度均为N=106。（a）γ=0.5，0.7，t=1.5时度分布图，插图为γ=0.84度分布图；（b）为γ=0.86，t=1.5时度分布情况，插图为双对数坐标下度分布情况；（c）γ=0.90，0.94，0.96，0.98，t=1.5时的度分布以及双对数坐标下的度分布情况；（d）ER模型和BFW模型在t=1.5时生成網络度分布对比图。

由公式（2）、（3），并结合Price模型优先连接机制可知，当N→∞，其生成网络结构为无标度网络和均匀网络的组合，当只考虑时，按照无标度网络结构增长，幂指数随的γ调节而变化，当只考虑时，生成网络为均匀网络，其度分布也被证明服从泊松分布[13]。

而BFW模型中在阶段数K和衰减函数g（K）的限制下，大分支的生长被一定程度的抑制，渗流相变点之前，添加到系统中的随机连边主要位于孤立节点或小连通分支当中，因此与ER随机网络度分布相比，BFW模型下节点的度数会更集中于平均度数附近，大量数值模拟也证明了我们的分析结论，图1（d）为ER渗流模型和BFW渗流模型下t=1.5时的度分布对比，BFW模型节点度分布更集中于平均度

以上實验结果表明，γ<γc时，序参量具有自平均特性，而γ>γc时，序参量不具有自平均特性。该结论与经典ER渗流模型以及阿赫利过程下的渗流相变相比具有非常显著的差别。

4 结 论

本文基于混合连边机制提出了MBFW模型，并且研究了该模型下的网络结构变化以及渗流相变性质。大量实验结果表明，网络结构随着γ的增大而发生改变，在添边数为1.5N时，存在临界点γc∈（8.84，0.86），在和γ∈（γc，1），生成网络结构分别具有均匀网络特性和无标度网络特性。研究发现，γ对渗流过程具有显著地影响，结果表明当γ<γc时，MBFW模型只有一次相变；而当γ∈（γc，1）时，MBFW模型具有多级相变。此外，通过对比实验表明，在MBFW模型中，序参量的自平均性质也随控制参量γ的改变而变化，当 时，序参量具有自平均性；而当γ∈（γc，1）时，序参量具有随机震荡现象，不具备自平均性。该结论与经典ER模型以及阿赫利过程下的渗流相变相比具有非常明显的差别。

以上研究结果表明：通过控制BFW模型候选边结点的选取方式，可以有效控制生成网络结构类型。但是对MBFW模型加边数为1.5N之后的渗流现象仍有待进一步的研究，并且对异质网络结构下的渗流相变机理还需更严格的理论加以研究论证。

参考文献：

[1] AHARONY A，STAUFFER D.Introduction to percolation theory [M].S.l.：Taylor and Francis，2003.

[2] Klaus Dietz.Infectious diseases of humans：dynamics and control [J].Trends Parasitol，1992，8（5）：179.

[3] David Strang，SOULE saraha.Diffusion in organizations and social movements：from hybrid corn to poison pills [J].Annu Rev Sociol，1998，24.

[4] SAHINI M，SAHIMI M.Applications of percolation theory [M].S.l.：Taylor and Francis，2014.

[5] ROZENFELD HD，SONG C，MAKSE HA.Small-world to fractal transition in complex networks：a renormalization group approach [J].Phys Rev Lett，2010，104（2）.

[6] ERD?S P，R?NYI A. On the evolution of random graphs [J].Bull.Inst.Internat. Statist.，1961.

[7] D.ACHLIOPTAS，R M.D'SOUZA，J.SPENCER. Explosive percolation in random networks [J].Science，2009，323（3）：1453-1455.

[8] ZIFF RM. Explosive growth in biased dynamic percolation on two-dimensional regular lattice networks [J].Phys Rev Lett，2009，103（4）.

[9] CHO YS，KAHNG B，KIM D.Cluster aggregation model for discontinuous percolation transitions [J].Physical Review E，2010，81（3）.

[10] Oliver RiordanLutz Warnke.Achlioptas processes are not always self-averaging [J].Phys. Rev.E，2012.

[11] Chen，Wei，D'SOUZA R M.Explosive percolation with multiple giant components [J] Phys Rev Lett，2011，106（11）.

[12] PRICE D D S. Networks of scientific papers [J].Science，1965，149（3683）：510-515.

[13] Noga Alon，Joel H. Spencer.Random graphs [M].Hoboken，NJ，USA：John Wiley & Sons，Inc.，2000：155-181.