不同加载方式下的沥青路面结构动态响应分析
罗正德

【摘 要】借助ANSYS构建半刚型基层沥青混凝土路面的构造模型,并进行瞬态调研,获得路面构造在平均移动常量负载与半波正弦负载之下的竖向移动与竖向动应力时程曲线,即两类加载方法之中的路面构造,在动态响应之中的规律类似;不一致的加载方法仅凸显在极值产生的时间段与极值多少的较少间距之中。这一论断能够给沥青路面处于不一致动载之中的施工辅以参照。
【关键词】沥青路面;加载方式;动态响应
【中图分类号】U416.217 【文献标识码】A 【文章编号】1674-0688(2018)05-0153-02
0 前言
沥青路面构造之中的力学响应会被负载、构造种类、构造融合等各类因素影响,汽车速度快、多载等特征得以逐步凸显,路面构造在具体的动态型重载之中凸显出的力学特性与原本的静态模型间具备过量的差别。传统的静力学方法已无法全方位地凸显沥青路面构造之中的动力响应对于轴载、路面构造数值的敏感特性。对路面构造处于重载之中的动力响应数值进行调研,把握路面构造响应对于负载数值与路面构造数值产生的敏感特性尤为关键,能够帮助施工设计单位提升对重载型沥青路面构造设计的高效性。
1 三维型有限元分析模型
1.1 路面构造与原料数值
在调研期间,考虑到路面构造之中的阻尼对于动力响应的影响,把路面构造之中的阻尼比重ζ设定为0.05,依据路面构造模态进行调研,获得自振频次ω1与ω2,测算出Rayleigh型阻尼比重数值α=5.159(2ω1ω2 ζ/ω1+ω2)、β=3.623×10-4(2 ζ/ω1+ω2)。
1.2 负载数值
负载借助对道路沥青路面构造进行设计时运用的规范型轴载,单轴型双轮组为100 kN。借助半波型正弦平均分散负载测算动载,运作速率借助高速公路相应的设计速率(80 km/h),测算负载作用的周期T=0.058 s。轮胎的触地面积即矩形,矩形之中长宽比重为0.871 2/0.6。P(t)=Pmax×sin(π/Tt),Pmax为负载作用之中的峰值,规范轴为0.70 MPa;T为负载作用的周期,T=12a/v;v为汽车运行的速率;a为轮胎触地面积之中的当量圆半径,规范轴为0.106 5 m。
1.3 模型数值
有限型元模型的大小憑借应力测算成果收敛平稳作为凭据,平面大小为6.0 m×6.0 m,路基的深度为6.0 m,模型如图1所示。各大构造层借助八大节点六面体之中的全部积分单位即C3D8进行模拟[1]。因为构造与负载具备一致性,所以使用1/4型模型进行调研。边界借助路基底层施行竖向制约(z朝向),对各大构造层一致面施行一致制约,侧向(x朝向与y朝向)施行水平制约,x朝向即公路横向,y朝向即公路纵向。
2 不一致加载方法之中沥青路面构造相应的动态响应
2.1 两类加载方式之中测算处力学响应相应的变换规律
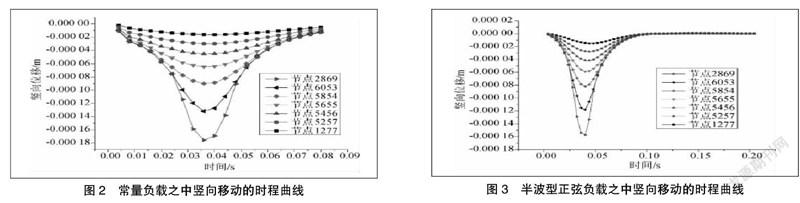
在图2之中,汽车处于起始处或终点处的期间,各处的竖向移动为0;运作的汽车愈趋近测算处,竖向移动愈多,在运行至测算处后,具备的竖向移动最多;汽车驶走后,测算处之中的移动逐渐回归为0,而移动得以全方位回归,这与路基及路面构造层原料所具备的弹性特性相关[2]。在图3之中,汽车的起始处与图2之中的起始处一致,然而,汽车负载的多少会在移动的同时产生变换,变换规律即半波型正弦函数,在Z=5.0 m位置的测算处,汽车逐渐趋近、到达直到逐步驶走后,其竖向移动经由0逐渐增多直至最高,再逐渐变小归0的规律加以变换,与常量负载之中的变换规律一样。在图2与图3之中,面层之上的移动数值最高,依据深度的增长逐步变小。
竖向之中的动应力大多为压应力,汽车处于起始处或是终点处后,动应力为0;汽车在移动逐渐趋近测算处后,测算处的动应力逐步增多;在到达测算处后,动应力最高;接着汽车逐步驶走,测算处的动应力逐步变小直至回归为0;随着汽车逐步驶远,测算点的动应力不会被影响,保持为0,体现为某一零刻度部位的水平直线。
然而,不一致深度点之中的测算处所包括的竖向动应力曲线,在变换期间依旧具备不一致性[3]。对竖向动应力之中的时程变换进行调研,面层表层的节点即2 869,仅有在汽车将要到达后,才会具备瞬时增多的竖向压应力,汽车间距其过远时,节点之中的竖向压应力不具备变换,保持为0。在面层之下的10 cm深度的节点即6 053,这一突变具备缓和性,然而竖向动应力的范畴有所扩充;其往下愈深,测算处之中的竖向压应力产生的突变越不突出,然而竖向压应力的范畴逐步增大。例如,在面层表层之下的深度为60 cm时,这一位置之中的节点即1 277,竖向动应力的时程曲线较平,然而在汽车开启与驶走期间,这一节点都具备竖向压应力。如此就明确了越趋近路表,竖向应力越汇集,路表朝下越深的竖向应力越分散。
在常量负载之中,竖向最多移动与最高动应力都高过波动负载之中的数值,即因为常量负载长时间凭借稳固的压力作用到路面构造之上,而波动负载仅有在峰值点时才与常量负载的稳固压力数值一样,其余时间作用到路面之中的数值都少于稳固压力[4]。依据加载的时间进程进行测算,波动负载在移动至Z即5.0 m后的测算处,趋近峰值又未达到峰值,所以这一位置之中的竖向移动与竖向动应力都过少。最高竖向移动与竖向动应力产生的时间依据测算处的深度增加而逐步落后,而在波动负载之中,这类最高值产生的时间与波动峰值产生的时间紧密相关。
2.2 波动负载之中不一致部位测算处力学响应的变换规律
对于某大稳固部位点的测算处而言,负载间距其越近,对其所产生的影响就越大;负载间距其越远,对其所产生的影响就越小。总体而言,负载只有在测算处相邻的相应范畴之中,才会对其产生力学响应的影响[5]。例如,负载在作用至Z=5.0 m的测算处后,Z=6.4 m的测算处之中的竖向移动与竖向动应力相应的数值为0,曲线体现为某一在零刻度部位之中的水平直线;而在负载作用至Z=6.4 m的测算处后,Z=5.0 m的测算处的竖向移动与竖向动应力相应的数值也为0,曲线也体现为某一在零刻度部位之中的水平直线。
3 结语
对路面之中的某大稳固处来说,常量负载与波动负载之中的竖向移动与竖向动应力相应的时程变换规律类似。借助调研不一致深度之中测算处的竖向动应力相应的时程曲线变换规律发现:越趋近路层,竖向应力越汇集;路层朝下越深的竖向应力越分散。把路面构造稳固处的竖向移动与竖向动应力相应的极值辅以列表,指出不一致加载方法仅凸显在极值产生时间与极值多少的过少间距之中。
参 考 文 献
[1]许新权,吴传海,周勇,等.多层位移计在长寿命沥青路面动态响应测试中应用研究[J].公路,2016(8):7-11.
[2]杨毅,刘忠,辛亚兵,等.动载作用下半刚性基层沥青路面应变响应的演化规律[J].中外公路,2017(2):51-55.
[3]王甲辰,李浩,吴传海,等.湿热重载地区长寿命沥青路面动态响应实测系统研究[J].中外公路,2016(3):58-63.
[4]张丽娟.重载作用下沥青路面结构动态响应敏感性分析[J].上海师范大学学报:自然科学版,2015(2):138-145.
[5]陈峙,王铁,谷丰收,等.典型路面激励下的工程专用自卸车车架动态响应研究[J].汽车技术,2015(3):16-20.
[责任编辑:陈泽琦]

