超磁致伸缩执行器精密位移控制研究

王继骁　邵青伟　赵俊杰

摘 要：超磁致伸缩材料（GMM）是一种新型的功能性材料，具有应变大、可控精度高等优点，是研制精密驱动器的理想材料。本文阐述了在交变磁场中超磁致伸缩棒产生震动，通过对超磁致伸缩执行器（GMA）进行控制，使其输出的震动位移在我们要求的位移误差范围内，建立了超磁致伸缩位移控制模型并搭建了实验平台，最终实现了GMA的振动位移误差在1μm的误差范围内，GMA的输出达到了理想精度要求。

关键词：超磁致伸缩制动器；控制方法；滤波方法；交变磁场

中图分类号：TN712.2 文献标识码：A 文章编号：1003-5168（2018）04-0072-02

Research on Precision Displacement Control

of Giant Magnetostrictive Actuator

WANG Jixiao SHAO Qingwei ZHAO Junjie

（Shenyang University of Technology， Shenyang Liaoning 110870）

Abstract： Giant magnetostrictive material （GMM） is a new type of functional material with the advantages of large strain and high controllability. It is an ideal material for the development of precision actuators. This paper described the generation of vibrations in an alternating magnetic field by controlling the Giant Magnetostrictive Actuator （GMA） so that the output vibrational displacement was within the range of the displacement error we require. The displacement control model was extended and the experimental platform was set up. Finally， the vibration displacement error of GMA was within the error range of 1μm， and the output of GMA reaches the ideal accuracy requirement.

Keywords： giant magnetostrictive brake；control method；filtering method；alternating magnetic field

超磁致伸縮材料（GMM）是20世纪70年代迅速发展起来的智能材料，具有伸缩系数大、机电耦合系数大、响应速度快、承载力强等优点[1]。在外加磁场的作用下，GMM会沿磁化方向发生伸长或缩短变形，利用这一原理制成的超磁致伸缩驱动器（GMA）具有响应时间短、负载力大、低频性能好等特点。基于其特性设计出的前馈逆补偿PID控制器用于大行程GMA驱动位移精密控制，得到纳米级别的定位精度。本文采用LMS算法对GMA进行实时控制，控制方法不依赖于物理模型，因此较为方便简捷。

1 超磁致伸缩执行器（GMA）的结构模型

本实验所用到的超磁致伸缩执行器的总体结构主要包括：碟形弹簧、传动轴、不锈钢上盖、预紧螺母、螺栓、紧固螺母、不锈钢中盖、上导磁片、纯铁套筒、不锈钢套筒、上导磁块、线圈骨架、GMM棒、下导磁块、防磁钢圈、下导磁片、不锈钢底座和线圈，共18个部分组成。在GMA整体系统中，将GMM固定在底座，顶端自由无约束且无任何能量损失的圆柱形棒体。

实验中使用的超磁致伸缩棒的长度为44mm、直径为12mm大小的TbDyFe材料，线圈匝数为600匝。试验系统利用日本NF可控电源为GMA提供交流电，激光位移传感器在传动轴处采集位移信号，通过PCI-1741U板卡采集信号到计算机，通过Labview与Matlab结合进行信号处理与控制编程。

2 LMS算法的基本原理

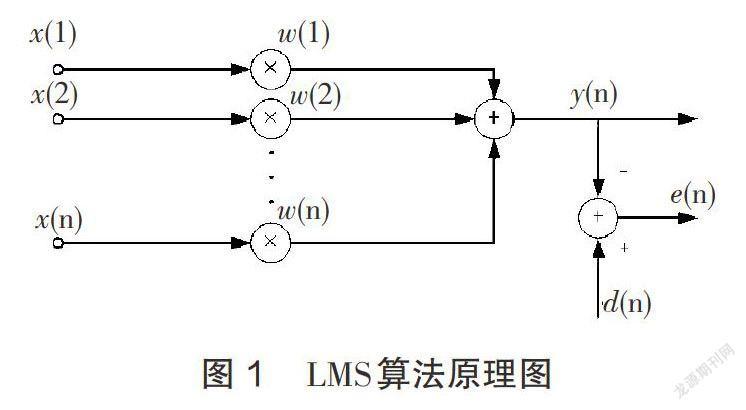
LMS算法基本原理如图1所示。

输出信号[yn]为激光位移传感器采集到的一系列震动位移信号：

[yn]=[i=0N-1winxn-i=WTnXn] （1）

定义权向量：

[Wn=W1n，W2n，…，WN-1nT] （2）

[Xn=xn，xn-1，…，xn-N+1T] （3）

令[dn]代表“所期望的输出位移”，并定义误差信号：

[en=dn-yn] （4）

误差信号的平方值近似该时刻的均方误差：

[εn≈e2n=dn-yn2] （5）

[?n=?e2n?W=-2enXn] （6）

通过最陡下降法可以得到[Wn]的迭代公式：

[Wn+1=Wn-μ?n] （7）

[μ]为收敛因子，[?n]为期望位移与实际位移的均方误差。LMS算法就是根据式（7）不断调节输出信号控制电源使输出位移的误差[en]达到最小值。

3 超磁致伸缩执行器的控制方法

GMA驱动器的控制原理：通过PCI-1741U板卡采集激光位移传感器的输出位移信号导入到LabVIEW中，然后通过控制程序给电源加载交变电压信号，控制器通过不断调节输出的电压信号，使GMA的输出位移不断改变，从而达到我们所需要得到的控制精度。

设激光位移传感器的输入位移信号为[yn]，所期望的位移为[dn]，输入的一组初始值为[Xn]，[μ]为收敛系数，取0.2，则根据第一次输入的一组信号求出[yn]的初始值为：

[yn=wn*Xn] （8）

求出期望信号与实际输出信号的误差：

[en=dn-yn] （9）

根据LMS算法中最陡下降法原理最终求出：

[wn=wn+2*μ*en*Xn] （10）

通过对输出的[yn]反复进行控制最终达到理想的期望信号。

为了验证辨识算法的有效性，分别以频率为30Hz，幅值为[40μm]的期望信号和[60μm]的期望信号进行控制，控制收敛因子[μ]设为0.02，控制输入初始值[Xn]取第一次输入的激光位移传感器的输出信号，控制系统以初始值0.1A，30Hz的电流进行第一次输入。激光位移传感器对应位移为：0.001V对应2.5μm，实验结果如图2所示。蓝色实线代表初始位移波形，红色实线代表控制后激光位移传感器输出的波形。通过BP4610双极性电源读取控制后的电流分别对应为[40μm]对应的电流值为0.7A，[60μm]对应的电流值为1.2A。

通过对比图可以看出，在期望位移为[40μm]的控制下电流值为0.7A，期望位移[60μm]的控制下电流值为1.2A。误差小于0.000 4V的激光位移传感器采集电压，对应的控制位移误差小于1μm，对应最终控制电流为0.7A，30Hz的交流电，实验结果达到理想的控制目的。

4 结论

通过上述理论分析以及实验研究可以得出以下结论：通过LMS算法对GMA进行控制可以得到一个比较高的精度，其误差在1μm范围内，对其精度的控制已经达到一个理想的范围。虽然控制过程中还存在噪声的干扰，且由于其参考电压的数值比较小，造成控制过程中还是会产生一定的偏差，但该控制方法与实验为以后的研究及应用奠定了一定的基础。

参考文献：

[1]徐彭有.超磁致伸缩驱动器精密位移驱动控制研究[D].上海：上海交通大学，2010.