大围长可快速编码QC-LDPC码的构造
冯志宇,彭海英,郭振勇,胡 蓉
(1.重庆邮电大学 光电学院,重庆400065;2.重庆邮电大学 移通学院,重庆 401520)
0 引 言
低密度奇偶校验(low-density parity-check, LDPC)码由Gallager[1]于1962年所提出,它是一种性能逼近Shannon限的好码。近年来,大量的研究人员为了获得高效的LDPC码,提出了各种LDPC码的构造方法。根据构造方式的不同,大致可以分为2种:①随机构造法,根据一定的设计准则利用计算机搜索构造所需要的校验矩阵;②结构化构造法,利用代数方法或者组合方法确定性构造所需要的LDPC码校验矩阵。
准循环低密度奇偶校验(quasi-cyclic low-density parity-check, QC-LDPC)码[2]是结构化LDPC码中一个支系,占据着重要的位置,可以由指数矩阵和扩展维数表示得到的码字结构。以往我们主要关注校验矩阵的构造,使之满足无短环或其他条件的要求,但是实际上编码复杂度也是制约码字性能及实际应用的一个重要因素。Richardson等[3]通过对校验矩阵执行分块和行列变换,将复杂度降为O(n+g2)。当g数值较大时,复杂度也会呈近似二次方增长。Myung等[4]利用QC-LDPC码准循环特点,把校验矩阵的校验部分直接设计成近似下三角结构,达到快速编码和降低复杂度的双重效果。已经提出的典型具备近似下三角结构的编码方案有双对角线结构[5]和准双对角线结构[6],可以直接通过校验矩阵进行迭代,求得校验码元序列,最后完成编码,并已在实际通信系统中得到了应用。
此后众多研究人员对上述校验部分进行了深入研究,提出了一些有效且结构良好的编码方案。然而,这些在双对角线基础上改进的方案,双对角线为单位矩阵或一对角线为单位矩阵,另一对角线为移位矩阵,形式固定且列重为2。Tam等[7]提出的改进方案中第一列列重设为3,但是对这3个移位矩阵系数做出了限制。此外,以往研究人员主要关注校验部分的设计,对信息部分矩阵的设计研究较少,构造出的校验矩阵中存在少量的四环和大量的六环,对码字的性能有一定的不利影响。王汝言等[8]提出了一种大围长低复杂的QC-LDPC码,码字性能优异。但是该构造方法分别独立设计校验矩阵的信息部分和校验部分,最后验证得到的校验矩阵围长为8,其构造过程证明繁琐。因此,怎样通过直接构造校验矩阵使之同时兼容大围长和快速编码双重特性是一个值得深入研究的课题。
本文针对上述难题,设计了一种大围长可快速编码的QC-LDPC构造方法。首先提出一种结构新颖更加灵活适合构造大围长QC-LDPC码的低复杂度快速编码方案,其次对利用最大公约数(greatest common divisor, GCD)算法得到的指数矩阵进行行列操作,验证得到的新指数依然满足大围长的特性,最后与掩饰矩阵和快速编码方法相结合,达到了QC-LDPC码大围长和快速编码的目的。本文所提方法无须对QC-LDPC码的信息部分和校验部分分别构造,而是直接在围长为8的原指数矩阵上通过一系列变化来实现低复杂度的快速编码。最后,通过仿真验证了所构造的QC-LDPC码的优异性能。
1 基于GCD算法的QC-LDPC码
QC-LDPC码是一种高度结构化的LDPC码,其校验矩阵H是由单位矩阵循环移位后的循环置换矩阵组成。该矩阵形式为[9]
(1)
(1)式中,Hj,l=I(pj,l)表示校验矩阵中的子矩阵,其中,1≤j≤J,1≤l≤L,I(pj,l)表示将一个P×P的单位矩阵向右循环移位pj,l位得到的循环置换矩阵。根据QC-LDPC码的循环特性可以得到对应的指数矩阵为
(2)
因此,QC-LDPC码的构造可以归结为指数矩阵E的设计。QC-LDPC码的校验矩阵由循环置换矩阵和零矩阵构成,这一特点使其可以通过简单的移位寄存器实现线性编码,且只需要1/P的存储空间。
在指数矩阵中,如果若干个元素(p1,p2,…,p2l)构成一个长度为2l的环,则对应的校验矩阵H中也存在与之对应的P个同样大小的环。可以看出在QC-LDPC码的校验矩阵中,短环是以集合的形式出现。QC-LDPC码中长为2l的环可以表示为(j0,l0),(j1,l0),(j1,l1),…,(jl-1,l0),(j0,l0),其中,(jk,lk)表示H矩阵第jk行lk列所在的循环子矩阵I(pjk,lk)。(jk,lk)和(jk+1,lk+1)之间的子矩阵可以看作(jk+1,lk)。显而易见,要正确地表示一个环,需满足jk≠jk+1,且lk≠lk+1。文献[10]提出长度为2l的环检测定理。
定理1对于指数矩阵E中的序列pj0,l0,pj1,l0,…,pjl-1,l0,pj0,l0,其中,pjk,lm和pjk,ln在同一行或同一列,pjk,lm和pje,lf在不同行且不同列,则pj0,l0,pj1,l0,…,pjl-1,l0,pj0,l0构成长为2l环的充分必要条件是
(3)
短环的存在会导致LDPC码在译码时相关信息经过2次迭代后互相关,产生错误传播信息,译码收敛速度减慢,甚至不能收敛,造成误码比特率(bit error rate, BER)性能变差。因此,若要使构造的QC-LDPC码中不含长为2l的环,就必须通过一定的设计规则,使得(3)式不成立。图1给出了6环存在的6种形状。
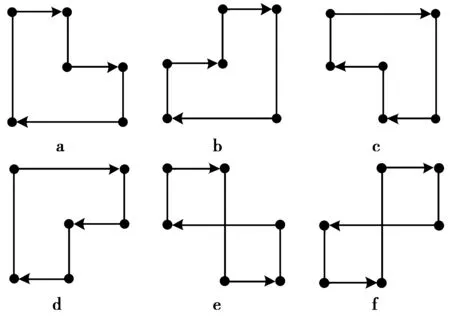
图1 6环的6种形状Fig.1 Six types of six cycles
张国华等[11]提出了一种基于GCD算法构造的QC-LDPC码,得到的码字无4环和6环,且具有大围长特性。其指数矩阵形式为
(4)
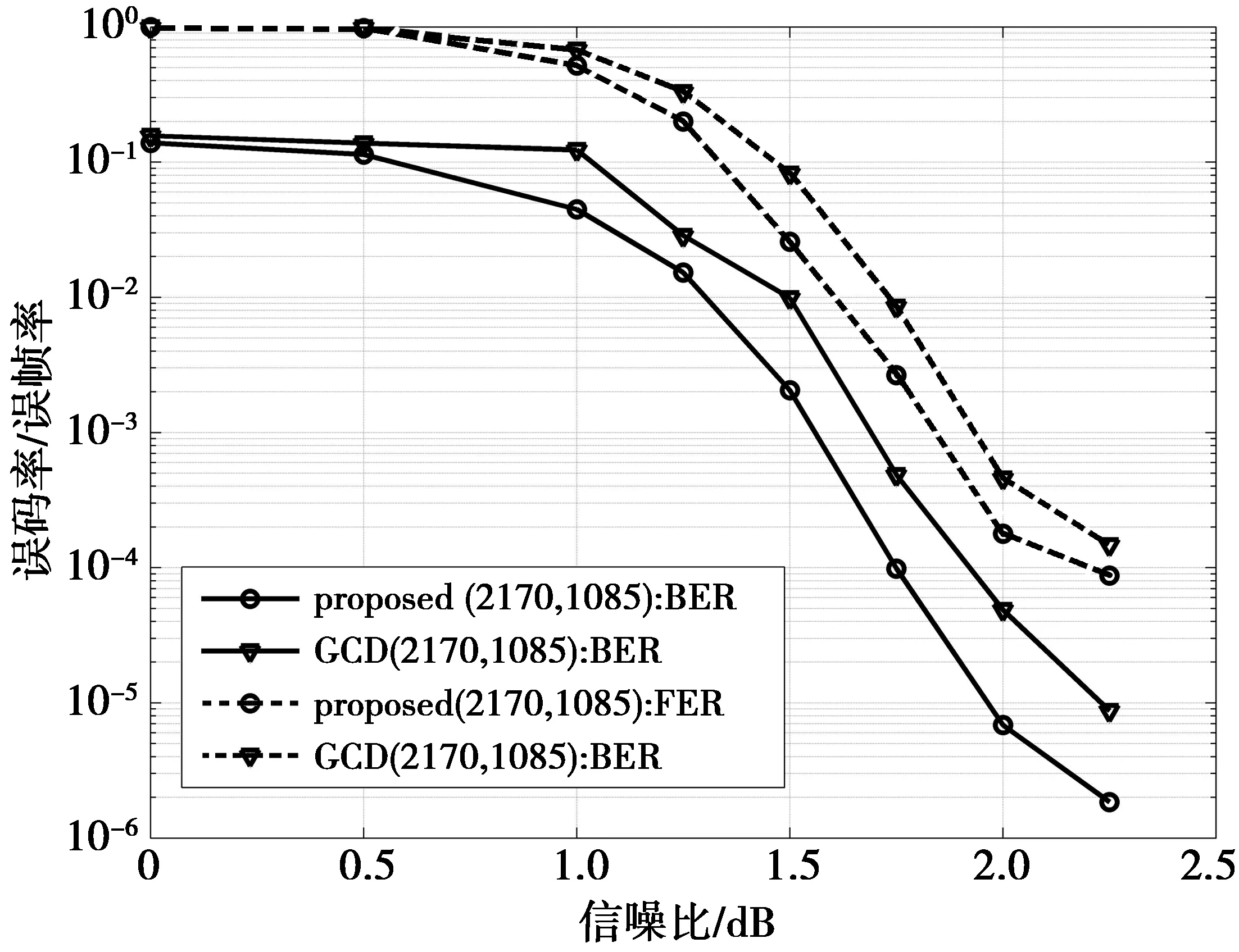
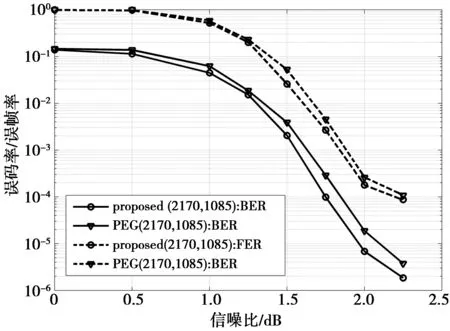
每个单位矩阵的移位值为pj,l=aj-1·(l-1),其中,j=1,2,…,J;l=1,2,…,L;0≤a0 通过研究我们知道无论是采用传统编码还是高斯消元法,其编码复杂度较高,不利于实际应用。经过研究人员的不懈努力及QC-LDPC码的发现,提出了众多快速编码方案,降低了编码复杂度,取得了优异的码字性能。本文提出一种改进型下三角结构的快速编码算法,灵活性更好,对直接构造大围长可快速编码的QC-LDPC码有很大的促进作用。 将QC-LDPC码的校验矩阵H分为(5)式所示的2部分。 H=[HkHp] (5) 信息部分矩阵Hk为 (6) 快速编码算法主要是对校验部分Hp的构造,本文所提出的可快速编码算法的校验部分Hp矩阵为 (7) (7)式中,hi,j表示校验部分矩阵Hp的第i行,第j列的非单位矩阵,2≤i≤M,1≤j≤M。第1列3个子矩阵对应的移位值非零且不相等,从第2列到最后一列每一列的hi,j只有1个非零移位值且是随机存在的,也即列重是2。 将码字序列c分为2部分:信息比特序列和校验比特序列,如(8)式所示。 c=[sp] (8) 由码字生成式HcT=0,把(5)式和(8)式代入其中可得: HksT=HppT (9) 把(6)式和(7)式代入(9)式展开后形式为 (10) 然后对矩阵的每一行进行计算,得到以下等式: (11) i=2,…,M-3 (12) i=M-2 (13) i=M-1 (14) i=M (15) 由(11)式和(12)式可求得pi(i=2,…,M-2)为 (16) 根据(13)式和(14)式求得pM-1,pM分别为 (17) 根据(15)式可得p1为 (18) 由上述一系列式子可以看出,校验比特序列可以直接以简单迭代的方式逐一求出,进而与信息比特序列结合起来组成码字c,最后完成编码。 编码复杂度主要是对编码过程中产生的乘法运算次数、加法运算次数、存储复杂度来进行分析。乘法运算和加法运算的运算量直接决定着运算复杂度,而这一点正是能否实现线性快速编码的关键。因为构造的校验部分矩阵Hp第2列至最后一列每列列重为2,且非零移位值hi,j是随机存在的,为了计算复杂度,对第2列至最后一列取hi,i(2≤i≤M)为非零值。下面对上述提出的快速编码算法计算乘法和加法次数,结果如表1所示。表1中,R表示码率,P表示指数矩阵的扩展维数,n表示LDPC码的码长,且n=N×P。 表1 快速编码算法的计算复杂度Tab.1 Computation complexity of fast encoding algorithm 对表1结果分析可知,每个校验位分矢量的计算复杂度为O(n)。这说明使用该形式构造的QC-LDPC码编码复杂度与码字的码长成线性关系,能实现线性快速编码,为后面构造大围长可快速编码的QC-LDPC码奠定了基础。 一般情况下构造低编码复杂度的快速编码方法,研究人员更多关注的是校验部分的构造,信息部分常常采用随机方法或者其他方案,对构造的码字围长考虑较少,存在数量较多的短环,而短环的存在会严重影响码字性能。文献[8]提出的大围长快速编码方法是分别独立构造指数矩阵的信息部分和校验部分,然后证明围长为8,使得构造的LDPC码同时具备了大围长和低编码复杂度的可快速编码的双重特点,最后仿真验证了码字性能。 上述方案都是分别对校验矩阵的2部分进行构造,不管是构造方法还是围长都存在不足。观察上述快速编码方案可知,若采用GCD算法直接构造指数矩阵,然后把其校验部分转化为(7)式,受制于对角线上单位矩阵的存在,势必会影响最后得到的码字围长大小状态。本文利用GCD算法构造的指数矩阵的某一行或某一列加减相等的公差,不影响围长的大小,依然保持围长为8的特性。下面围绕定理2展开讨论。 定理2如果基于GCD算法构造的QC-LDPC码没有4环、6环存在,则分别对指数矩阵中的某行或某列加减相等的公差后,所得到的指数矩阵围长不变。 证明围长大小不变意味着指数矩阵中不存在4环和6环,下面分别验证2种环状态。 1)无4环验证。不失一般性,任取指数矩阵中一个2×2维的子矩阵,令0≤i air-ais+ajs-ajr≠0(modP) (19) 设公差为di≥0,dj≥0(0≤i,j≤J-1),对指数矩阵的任意2行的数值进行加减公差操作。若存在4环,则根据环检测定理得到的充要条件为 (air+di)-(ais+di)+(ajs+dj)- (ajr+dj)=0(modP) (20) 对(20)式计算可得: air-ais+ajs-ajr=0(modP) (21) (21)式与 (19) 式矛盾,故不存在4环。同理,对指数矩阵的任意2列也执行上述同样的操作,可证明也不存在4环。进而可知,对指数矩阵的某行或某列加减相等的公差不会存在4环。 2)无6环验证。根据图1可知,矩阵中存在6环有6种情况。不失一般性,任取指数矩阵的3行3列,即0≤i air-ais+ajs-ajt+akt-akr≠0(modP) (22) 设公差di≥0,dj≥0,dk≥0(0≤i,j,k≤J-1),对指数矩阵的任意3行的数值进行加减公差操作。若存在6环,则根据环检测定理得到的充要条件为 (air+di)-(ais+di)+(ajs+dj)-(ajt+dj)+ (akt+dk)-(akr+dk)=0(modP) (23) 对(23)式计算可得: air-ais+ajs-ajt+akt-akr=0(modP) (24) (24)式与 (22) 式矛盾,故不存在6环。同理,对形如图1a指数矩阵的任意3列也执行上述同样的操作,可证明也不存在6环。同样,可以对6环存在的其他5种形状用上述证明方法进行证明也不存在6环。所以,对指数矩阵的某行或某列加减相等的公差不会存在6环。 因此,由定理2可知,对利用GCD算法得到的确定性指数矩阵的某行或某列加减相等的公差,不会影响围长的大小,即新得到的指数矩阵围长依然为8。运用此定理,首先使用GCD算法对序列A={a0,a1,…,aJ-1}进行搜索,得到确定的指数矩阵。然后对指数矩阵的行或列进行加减公差运算,使得其校验部分转化为上述提出的快速编码算法形式,即对角线为单位矩阵。然后利用掩饰技术[12]不会影响围长大小的特点设计掩饰矩阵,最后得到的指数矩阵同时满足围长为8和快速编码的特性。 本部分在AWGN(additive white Gaussian noise)信道下进行仿真,调制方式采用二进制相移键控(binary phase shift keying, BPSK),译码方式采用置信传播(belief propagation,BP)算法,最大迭代次数设置为100。 首先,利用GCD算法构造一个维数为5×10的指数矩阵。分别设置参数列重J=5,行重L=10,通过GCD算法搜索得到序列{a0,a1,…,a4}={0,1,10,11,23},根据 (4) 式计算得到确定的指数矩阵为 E= (25) 然后,根据本文提出的快速编码算法,通过对指数矩阵中校验部分的数值进行加减数值,使对角线数值变为0,也即单位矩阵。得到新的指数矩阵为 E= (26) 掩饰技术[12]不会改变围长的大小,利用此性质可以灵活设计掩饰矩阵,不仅能满足快速编码算法第2列到最后一列除单位矩阵外另一个数值随机分布的特点,而且能使校验矩阵整体更加稀疏,有效地提高码字的性能。掩饰矩阵M(5,10)设计为 (27) 最后,得到的指数矩阵为 E= (28) 仿真1当扩展维数取P=217时,根据上述指数矩阵得到非规则(2 170,1 085)码与原始基于GCD算法构造的同等码长、码率、围长为8的QC-LDPC码的误码率(bit error rate, BER)、误帧率((frame error rate,FER)性能对比,结果如图2所示。 图2 与GCD算法的QC-LDPC码性能比较Fig.2 Comparison of the error performance for GCD QC-LDPC codes 由图2可知,与基于GCD算法构造的围长为8的QC-LDPC码相比,本文提出的基于GCD算法的快速编码方法在误码率为10-5时,获得了0.25 dB的编码增益。另外,本文所提出的码字可以利用校验矩阵直接进行编码,不仅围长不会减小,而且能实现线性快速编码。 仿真2渐进边长(progress edge growth, PEG)算法[13]是一种随机算法,虽然实际应用难度较大,但以其自身优异的码字性能成为众多研究人员构造LDPC码相比较的对象。图3是本文构造的(2 170,1 085)非规则QC-LDPC码与同等码长、码率等指标一致的基于PEG算法构造的随机码性能比较。 图3 与PEG算法的LDPC码性能比较Fig.3 Comparison of the error performance for PEG LDPC codes 从图3中可以看出,本文构造的QC-LDPC码在误码率为10-5时,码字性能与PEG算法相比提高了约0.1 dB。也从侧面证实了结构化LDPC码具有不输于随机化LDPC码的码字性能。 本文针对影响LDPC码码字性能的高编码复杂度的问题,提出了一种具有线性编码复杂度的可快速编码方案。该方案相较经典的近似下三角结构灵活性更高,更适合构造大围长的QC-LDPC码。证明了对基于GCD算法构造的指数矩阵的行列进行加减数值运算不改变围长的大小。最后采用掩饰技术与提出的快速编码方案相结合,使得构造的QC-LDPC码同时兼容了大围长和低编码复杂度的双重特性。由仿真部分可以看出本文构造的QC-LDCP码性能优异,且无误码平层。2 大围长可快速编码的QC-LDPC码设计
2.1 一种快速编码算法及编码复杂度分析

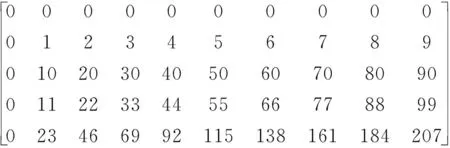
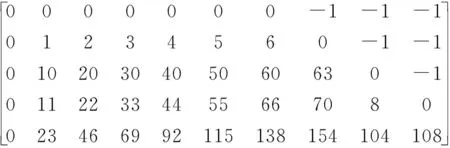
2.2 符合可快速编码的大围长QC-LDPC码设计
3 仿真与分析

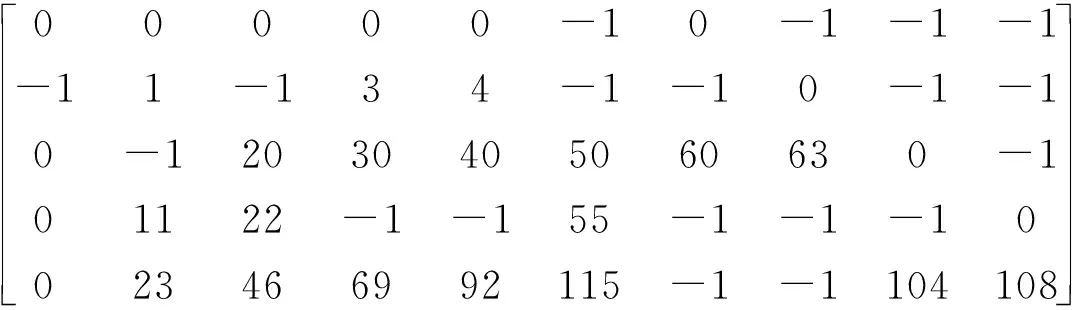
4 结束语

