THREE NONTRIVIAL SOLUTIONS FOR A NONLINEAR ANISOTROPIC NONLOCAL EQUATION∗
Amin ESFAHANI
School of Mathematics and Computer Science,Damghan University,36715-364 Damghan,Iran
E-mail:esfahani@du.ac.ir;amin@impa.br
Abstract In this article,we establish the existence of a sign-changing solution and two signconstant solutions for nonlinear nonlocal problem involving the BO-ZK operator on bounded domain.Our main tool is constrained minimization on appropriate Nehari manifolds.
Key words sign-constant and nodal solutions;BO-ZK operator;variational method
1 Introduction
The Benjamin-Ono-Zakharov-Kuznetsov(BO-ZK)equation

was first proposed in[32]as a model to describe the electromigration in thin nanoconductors on a dielectric substrate,here H stands for the Hilbert transform in the x-variable.In[4,5,36],equation(1.1)was generalized to

where L=(−∆x)α− ∆ywith α ∈ (0,1).The operator(−∆x)αstands for the fractional Laplacian in x-variable,which is defined,up to a constant Cn,α,by

When α =1,(−∆x)αis the usual Laplacian −∆x.In the case n=1 and α =1/2,we note that(−∆x)α=H ∂x.We will call L the BO-ZK operator.Some local and global well-posedness results for(1.2)in R2were obtained in[36].The BO-ZK operator L in(1.3)is also observed in the study of parabolic equations for which local diffusions occur only in certain directions and nonlocal diffusions[4,5,14].More precisely it models diffusion sensible to the direction in the Brownian and Levy-Itˆo processes.See[3,22]for some results on regularity and rigidity properties of the BO-ZK operator L,and also Hölder and Lipschitz estimates for viscosity solutions of the elliptic and parabolic nonlinear integro-differential equations associated to L.
The present paper deals with the following Dirichlet-type boundary value problem

where Ω ⊂ RN=Rn×Rm,m,n ∈ N,is a bounded domain with Lipschitz boundary,Ωc=RNΩand f∈C1( Ω×R,R).
In[20],the authors used the concentration-compactness principle(see[33])and some commutator-type estimates and obtained the existence of ground states of(1.1)in the fractional Sobolev-Liouville space X(see Definition 1.1).See also[19].
Contrary to(1.3)which contains the anisotropic operator L,the nonlinear fractional Schrödinger equation

is well-known as a nonlocal model containing an isotropic operator.Equation(1.4)was first introduced by Laskin[30,31]through expanding the Feynman path integral from the Brownianlike to the Lévy-like quantum mechanical paths.Recently,the analysis of the standing wave solutions of(1.4)is of much interest,and attracts much attention in nonlinear analysis.
At present,there were a few results appeared in the literature for the characterization of the ground states of(1.4).By applying the variational methods,with a detailed analysis of a mountain-pass-type geometry,the authors in[10–13,39–41]studied the existence,regularity and properties of standing waves of(1.4).In[21,25,26]the authors obtained deep results about uniqueness and non-degeneracy of ground states for(1.4)in case f(u)=up.See[17]as a nice reference for the study of the fractional Laplacian and the fractional Sobolev spaces.
Definition 1.1(see[18]) Let m,n∈N and N=m+n.The fractional Sobolev-Liouville space X,is the set of all functions g∈L2(RN)such that

Remark 1.2 Note from[27]that
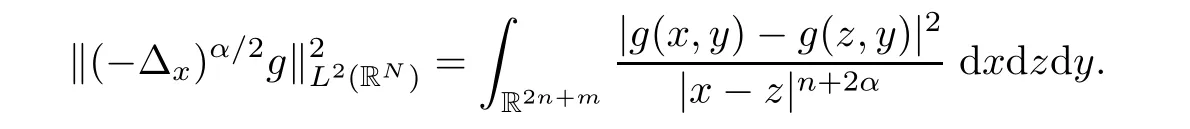
And X with the following inner product is a Hilbert space,

We recall the main embedding results for the fractional Sobolev-Liouville space X.
Theorem 1.3(see[18,Remark 2.2]) The fractional Sobolev-Liouville space X is continuously embedded into Lp(RN)for p ∈ [2,q∗];and is compactly embedded if p ∈ (2,q∗).
Remark 1.4 It is important noticing that one can define the space X in bounded domainΩ ⊂ RNif Ω satisfy a semirectangular condition(see[28]),that is Ω = Ω1× Ω2⊂ Rn×Rm;and Theorem 1.3 is still valid.More precisely the fractional Sobolev-Liouville space XΩon the bounded domain Ω is defined as the space of all g ∈ L2(Ω)such that

To study problem(1.3),we define a closed subspace
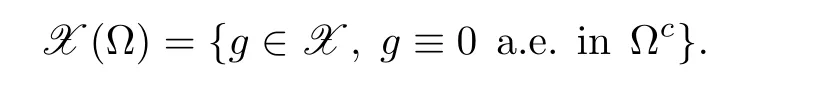
It is clear for g∈ X(Ω)that

Because of the fractional Sobolev inequality and Theorem 1.3,X(Ω)is a Hilbert space(see[9]and[41,Lemmas 7–9])with inner product
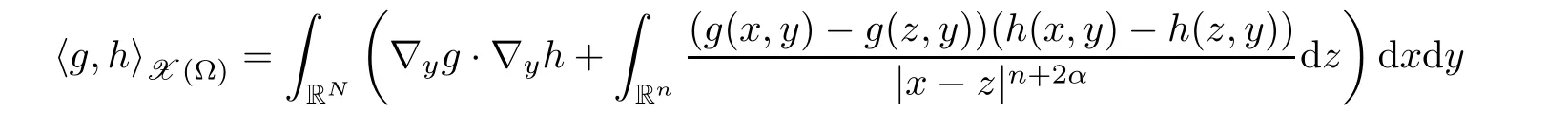
and this induces a norm kgk2X(Ω)=hg,giX(Ω).Observe from[17,Proposition 3.6](see also[18,27])that we have the following identity
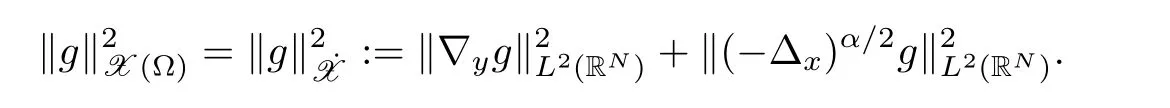
We assume that the nonlinearity f in(1.3)satisfies the following growth conditions.
(f1)uniformly for a.e.(x,y)∈ Ω.
(f2)There exist R>0 andµ>2 such that 0<µF(x,y,t)≤tf(x,y,t)for all(x,y)∈Ωand|t|≥R,where F(x,y,t)=Rf(x,y,s)ds.
(f3)uniformly for a.e.(x,y)∈ Ω,where
(f4)The function f(x,y,t)/t is increasing in|t|>0,for every(x,y)∈Ω.
For u∈ X(Ω),set

Then J ∈ C1(X(Ω))and for any ϕ ∈ X(Ω),
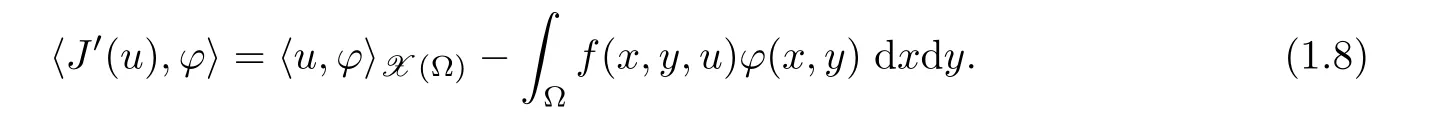
Moreover,all the critical points of J are(up to a normalization constant depending on α and N,which we will neglect henceforth)weak solutions of(1.3),namely,they satisfy,for all ϕ ∈ X(Ω),

Theorem 1.5 Let f satisfy(f1)–(f4).Then,problem(1.8)admits a nonnegative solution and a nonpositive solution which are not identically zero.
Definition 1.6 A solution u of equation(1.3)is called a ground state,if u satisfies

where N is the corresponding Nehari manifold of(1.3)given by

Theorem 1.7 Under assumptions(f1)–(f4),there exists a ground state of(1.3).
The proofs of Theorems 1.5 and 1.7 are variational and based on the mountain pass theorem[1,42].
Our next aim is to study the existence of the sign changing(nodal)solutions of(1.3).
Definition 1.8 We call u a least-energy sign-changing solution to(1.3)if u is a solution of(1.3)with u±6≡ 0 and
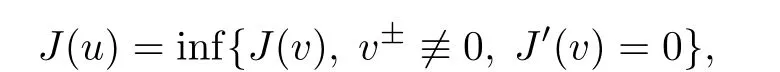
where u+(x)=max{u(x),0}and u−(x)=min{u(x),0}.
There are various methods in the literature to obtain sign-changing solutions for equations involving the elliptic-type operators.The classical operator is the local Laplacian and the semilinear elliptic equation

The frontier results were reported in[8]and[29].In[8],Berestycki and Lions used the minimax method and proved,under some Ambrosetti-Rabinowitz-type conditions[1],the existence of a radial sign-changing solution of(1.11).Jones and Küpper in[29]proved the radial sign-changing solutions of(1.11)by the dynamical systems approach.
Considering a(x)u+f(x,u)instead of f(x,u)in(1.11),Bartsch et al.in[6]used minimax arguments in the presence of invariant sets of a descending flow to prove the existence of a nodal solution for superlinear and subcritical nonlinearity f.They controlled the number of nodal domains by a nonlinear version of Courant’s nodal domain theorem.Furtado et al.in[24]obtained,under analogous assumptions on f,nodal solutions for(1.11)by seeking minimizers on the sign-changing Nehari-type manifold when a(x)may change sign and satisfy mild integral conditions.In bounded domains,Noussair and Wei in[35]established the existence of signchanging solutions via the Ekeland variational principle and the implicit function theorem.Bartsch and Weth in[7]combined the variational method to the Brouwer degree theory and show the existence of the nodal solutions without any geometrical or topological assumption on the domain except of boundedness.
To prove the existence of least energy sign-changing solutions,motivated by[7],we define the following constrained manifold
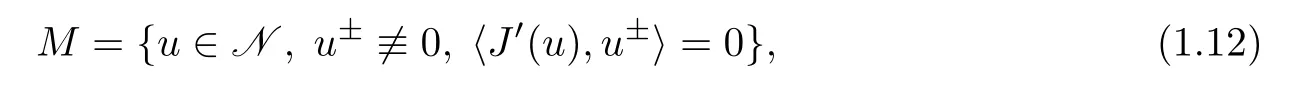
where

All methods mentioned above heavily rely on the following two decompositions

But equation(1.3)contains a nonlocal term and does not satisfy(1.13).So the above mentioned methods seem not to be applicable for(1.3).To overcome this difficulty,by borrowing some ideas from[43,44],we use a constrained minimization on the sign-changing Nehari manifold combined with the Brouwer degree theory(see[2,7])and proved that(1.3)has a sign-changing solution.We should remark that the method presented in[43]strongly depends on the fact that the nonlinearity is homogeneous,so it is difficult to apply it to deal with problems with more general nonlinearities.It requires a more delicate analysis.By using a different approach from[43],we establish for each u∈X with u±6=0 that there are positive constants t and s such that tu++su−∈M.Then it can be showed that there is a least-energy sign-changing solution of(1.3).Indeed we show by a quantitative deformation lemma and using the Brouwer degree theory that this solution is indeed a critical point of J.
Our main results are as follows.
Theorem 1.9 Assume that conditions(f1)–(f4)hold,then problem(1.3)has at least one least-energy sign-changing solution u∈ X(Ω).
Remark 1.10 However,in this framework,because of the nonlocal term(−∆x)αwe can not prove the exactly nodal domains corresponding to the sign-changing solution obtained in Theorem 1.9.
We also apply the ideas of Ros-Oton and Serra[38](see also[37])by proving a suitable variational inequality and give a nonexistence result of solution u ∈ W(1),r(Ω)of problem(1.3).The space W(1),r(Ω)is the generalized fractional Sobolev-Liouville space(see[18]).
Theorem 1.11 Let Ω ⊂ Rn×Rmbe a bounded star-shaped domain with respect to the origin satisfying the semirectangular condition,andW(1),r(Ω)for some r∈ (1,∞)m+n,is a critical point of J,then u ≡ 0 provided that f is supercritical,in the sense that

for all(x,y,t)∈Ω×R with t 6=0.
The concentration phenomena for(1.3)will be studied in forthcoming paper.Some concentration results associated to(1.4)can be studied in[15,16].
The paper is organized as follows.In Section 2,we show some estimates to check the validity of mountain-pass geometry.The Section 3 is devoted to prove the existence of sign-changing solutions of 1.3.The proof of Theorem 1.11 is given in Section 3.
2 Sign-Constant Solutions
In this section,we study the existence of sign-constant solutions of(1.3)through Theorem 1.5.The proof is based on mountain pass theorem by applying the following lemmas.
Lemma 2.1 Suppose that f satisfies(f1)–(f4).Then there exist ρ >0, β >0 and e∈ X(Ω)such that J(u)≥ β >0>J(e),for any u ∈ X(Ω)with kukX(Ω)= ρ Proof Let u be in X(Ω).It follows from(f1)and(f3)that for any ǫ>0 there exists Cǫ>0 such that for all t∈R and a.e.(x,y)∈Ω.Thus we have from Remark 1.4 that where C>0 is the constant of the embedding X(Ω)into Lq∗(Ω).Then by choosing ρ and ǫ sufficiently small such that β >0 we get J(u)≥ β. On the other hand,it follows from(f1)–(f4)and[40,Lemma 4]that for all t∈R and a.e.(x,y)∈Ω,where m(x,y)and M(x,y)are two positive measurable functions in L∞(Ω).Hence it follows for any t>0 and u ∈ X(Ω)with kukX(Ω)=1,that as t→+∞.Hence the proof is complete by choosing e=tu and t>0 sufficiently large. ? Lemma 2.2 Let f satisfy(f1)–(f4).Suppose that c ∈ R and the sequence{uj}is in X(Ω)such that Then{uj}is bounded in X(Ω). Proof For any j∈N,it easily follows from(f2)and(2.1)that where C1=C1(K,µ,|Ω|,q).On the other hand,it is deduced from(2.3)that{J(uj)}is a bounded sequence and which implies that This inequality together with(2.4)shows that Therefore{uj}is a bounded sequence in X(Ω). ? Lemma 2.3 Let f satisfy conditions(f1)–(f4).Suppose that{uj}is a bounded sequence in X(Ω)such that(2.3)holds.Then there exists u ∈ X(Ω)such that,up to a subsequence, Proof Since X(Ω)is a Hilbert space and{uj}is bounded in X(Ω),then it follows from Theorem 1.3 and Remark 1.4 that there is a subsequence,still denoted by{uj},and u∈ X(Ω)such that uj⇀ u in X(Ω),uj→ u strongly in Lq(Ω)and uj(x,y)→ u(x,y)a.e.in RN,as j→∞.Hence by(2.1)and the dominated convergence theorem we get and as j→∞.Thusly,we have from(2.3)that Therefore we deduce that and So that we have that We are now ready to give the proof of Theorem 1.5. Proof of Theorem 1.5 Since the functional J has the mountain pass geometry and satisfies the Palais-Smale condition,the existence of a nontrivial critical point u ∈ X(Ω)of J is obtained by the mountain-pass theorem[1,42].Moreover J(u)>0=J(0).In order to show the existence of a nonnegative solution of(1.8),we consider f±(x,y,t)=f(x,y,t)χ{±t≥0}(t).The conditions(f1),(f3)and(f4)are valid for f±,while(f2)is verified by f+and F+a.e.in Ωand for any t>R,and by f−and F−a.e.in Ω and for any t< −R.Corresponding to f±if we consider J±,we see that Moreover J±satisfy Lemmas 2.1–2.3.Note from[23,equation(2.10)]that e in Lemma 2.1 can be nonnegative by taking its positive part.Hence there exists a nontrivial critical point u±∈ X(Ω)of J±.We show that u+is nonnegative in RN.Let ϕ be the negative part of u+.Then ϕ ∈ X(Ω)and Therefore kϕkX(Ω)=0,so that u+≥ 0 a.e.in RN.We can analogously show that u−≤ 0 a.e.in Ω. ? Proof of Theorem 1.7 By Theorem 1.5 we obtained a nontrivial positive critical point u of J.We claim that Assume by contradiction that there is a sequence{un} ⊂ X(Ω){0}with kujkX(Ω)→ 0 such that J′(uj)=0,which implies that=RΩujf(x,y,uj)dxdy.By Theorem 1.3 and Remark 1.4,we note for any ǫ>0 that Then we can obtain a contradiction and thus the claim is right.Now we shall show that J is bounded from below on N.Indeed,if not,there exists a sequence{uj}⊂N such that J(uj)< −j,∀j∈ N.Similar to the proof of Lemma 2.1,we can get for any ǫ>0 that where C2=C2(ǫ,|Ω|),which implies that kujkX(Ω)→ ∞,as j → ∞.As in the proof of Lemma 2.2,we can obtain that{uj}is bounded in X(Ω),which is a contradiction.Thus J is bounded from below on N.Define Clearly,cmin≤J(u).Let{uj}⊂N be a minimizing sequence for cmin,i.e.,J(uj)→cminandwith Lemmas 2.2 and 2.3,{uj}is bounded in X(Ω)and it has a convergence subsequence,still denoted by{uj},such that un→ u0in X(Ω).Thus,u0∈ X(Ω)is a nontrivial critical point of J with J(u0)=cmin>0 and hence u0is a ground state positive weak solution of(1.3). ? In this section we show the existence of a least energy nodal solution of(1.3). We start with some technical lemmas. Lemma 3.1 There exists C>0 and ρ >0 such that kukX(Ω)≥ ρ and for all u ∈ N.Moreover ku±kX(Ω)≥ ρ for all u ∈ M. Proof For any u∈N,we have from(f2)and(2.1)that On the other hand,since u ∈ N,then it follows from(2.1),by choosing suitable ǫ>0,and Theorem 1.3 that and consequently we get kukX(Ω)≥ ρ >0. Similar to above,the last claim is directly deduced from the fact hJ′(u±),u±i<0. ? Lemma 3.2 Let u ∈ X(Ω)with u±6≡ 0.Then there are s>0 and t>0 such that hJ′(tu++su−),u±i=0. Proof For any s,t∈ R+and u ∈ X(Ω),it follows from(2.1)and Remark 1.4 that and similarly Hence there is σ1>0 such that for all s,t∈R+.From(f2),we have for all|t|>R and a.e.(x,y)∈ Ω.Hence it follows from the continuity of tf(x,y,t)on Ω×[−R,R]that for all(x,y)∈ Ω and t∈R(see(2.2)).This implies that Hence,there is σ2>0 such that for all t,s ∈ [σ1,σ2].The proof of the lemma is now complete from(3.2)and(3.5)by applying Miranda’s theorem[34]. ? Lemma 3.3 Suppose u ∈ X(Ω)satisfies u±6≡ 0 and hJ′(u),u±i ≤ 0.Then there are t,s∈[0,1]such that tu++su−∈M. To prove Lemma 3.3,consider,for u ∈ X(Ω)with u±6=0,the functions A:[0,+∞)×[0,+∞)→R and A:[0,+∞)×[0,+∞)→R2defined by Lemma 3.4 Let u be in M.Then A(t,s) Proof Since u∈M,then(1,1)is a critical point of A.By the continuity of A and the factwe get that A attains a global maximum in some point(κ,ν)∈ [0,+∞)× [0,+∞).If ν=0,then κ 6=0 and and consequently it follows from hJ′(u+),u+i<0 that Combining(3.7)and(3.8),we have Note from(f1)and(f4)that κ≤1 and the nonnegative function2F(x,y,t)is increasing in|t|with t>0 for any|t|>0.Hence which contradicts(κ,ν)being the global maximum point of A.Thus κ 6=0 and similarly ν 6=0.Through direct calculations,we see from hJ′(u),u±i=0,A′(κ,ν)=0 and(f2)that κ,ν ≤ 1.Now suppose by contradiction that(κ,ν)6=(1,1).Then,similarly to(3.9),we have Therefore A(t,s) The proof of(3.6)is straightforward.Indeed,we have for u∈M that Proof of Lemma 3.3 The proof is an immediate consequence of the arguments used in the proof of Lemma 3.3 using(f2)and(f4). ? Lemma 3.5 If csis the infimum of J on M and is achieved by w∈M,then w is a critical point of J. Proof The proof follows the same lines as in[2,Theorem 1.3].Suppose by contradiction that there is ℓ>0 and v ∈ X(Ω)such that kvk=X(Ω)=1 andcontinuity of J, fix r>0 such thatfor all ϕ ∈ Br(w)⊂ X(Ω).Let I=(a,b)×(a,b)⊂R2with 0 (i)(1,1)∈I and A(t,s)=0 in I i ff(t,s)=(1,1); (ii)cs6∈A(∂I)and{tw++sw−;(r,s)∈}⊂Br(w). Let r1>0 be such thatand B∩{tw++sw−;(r,s)∈ ∂I}= ∅.For each g ∈ X(Ω)we denote by Θ(τ)= Θ(τ,g)the unique solution of the system where d(g,Bc)=dist(g,Bc).Since hJ′(Θ(τ)),Θ′(τ)i<0,for all Θ(τ) ∈ B,the map τ 7→J(Θ(τ,g))is decreasing for any g ∈ B;moreover Θ(τ,g) ∈ B for all τ>0.Furthermore it follows from the definition of J and Θ that there exists τ0>0 such that J(Θ(τ,w)) ≤J(w)−,for all τ∈[0,τ0].Now define the maps γ:→X(Ω)and Λ:I→R2by It is clear that max(t,s)∈ IJ(γ(t,s)) This means that Λ has a zero ζ∈ I.Hence hJ′(γ(ζ)),γ(ζ)±i=0;which is a contradiction.? All the elements are now in place to mount a proof of Theorem 1.9. Proof of Theorem 1.9 Let{uj}be a minimizing sequence of J on M.Then it deduced from Lemma 3.1 that{uj}is bounded in X(Ω),and consequently for any p ∈ (2,q∗).Moreover,it can be supposed,without loss of generality,that there is u∈ X(Ω)verifying On the other hand,it is straightforward to see from(f1)and(f3)that from where it follows together with(3.11)that u±6=0.Lemma 3.2 implies that there are t,s>0 such that We have from(3.13)that Assume without loss of generality that s≥t.We deduce from(3.14)and(3.15)that which implies that s≤ 1.We show that J(tu++su−)=cs.We see from(3.14)that tu++su−∈M.Thus by the properties ofF,defined in the proof of Lemma 3.3,we obtain that Consequently,w=tu++su−∈M and J(w)=cs.Then Lemma 3.5 shows that w is a critical point of J with w±6=0. ? Finally we give the proof of Theorem 1.11. Proof of Theorem 1.11 Define,for any λ ≥ 1,the function uλ(x,y)=u(λx,λαy).Since Ω is star-shaped,uλ∈ X(Ω),and then we have from(1.8)that Now we differentiate both sides of(3.16)with respect to λ at λ =1+. First we obtain from u ∈ X(Ω)∩ L∞(Ω)∩ W(1),r(Ω)and Lemma 4.2 of[38](with slight modifications)that On the other hand,since Ω is star-shaped, The second term in the right hand side of(3.20)is nonpositive from(3.19),hence it follows from(3.19)and(3.20)that which is a contradiction to(1.14)unless u≡0.
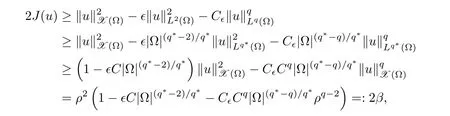

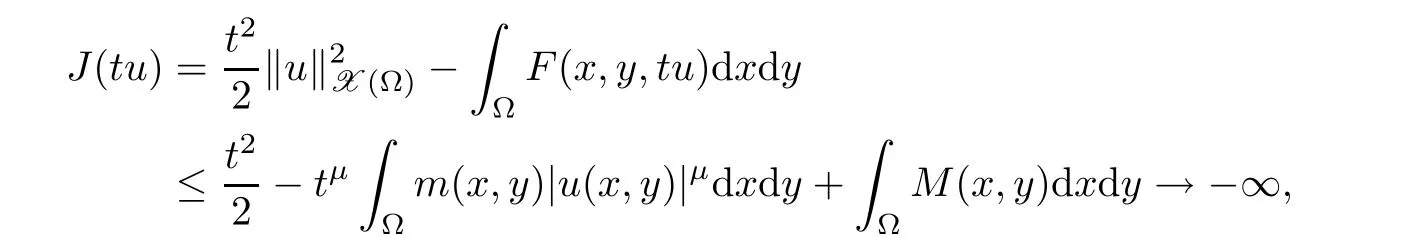

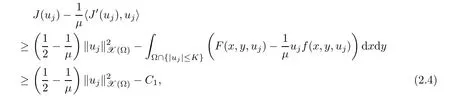



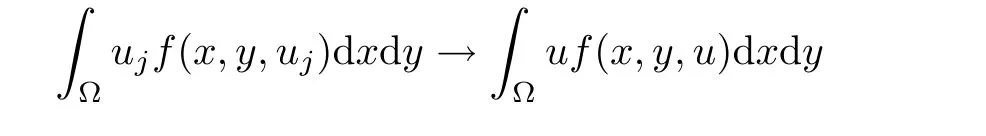
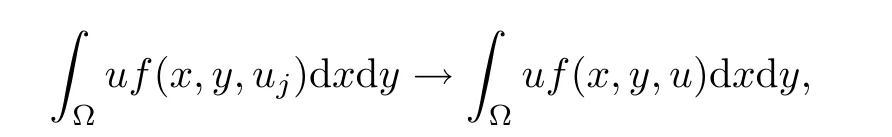





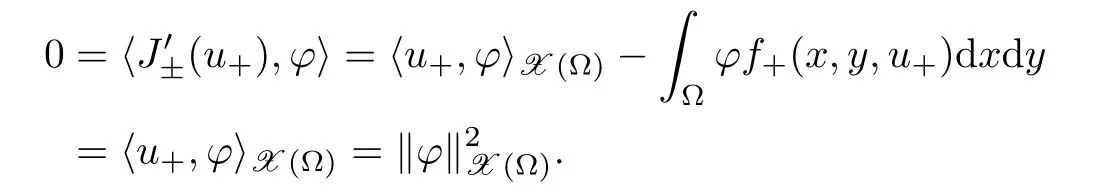
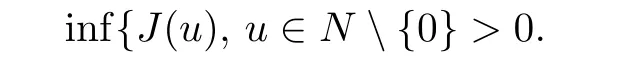
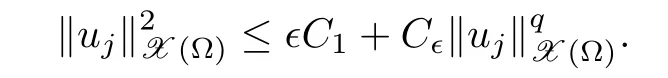

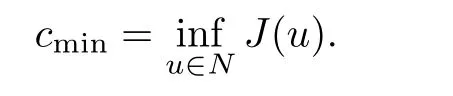
3 Sign-Changing(Nodal)Solutions

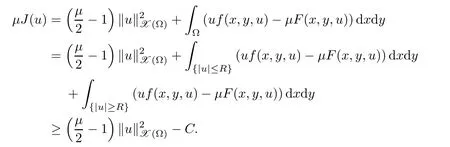


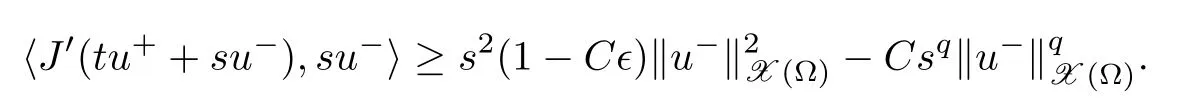

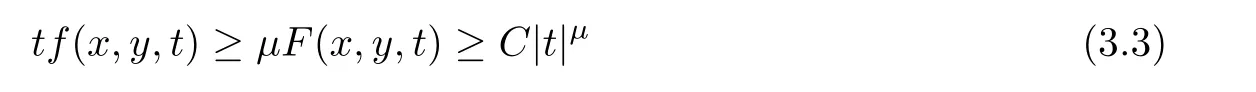


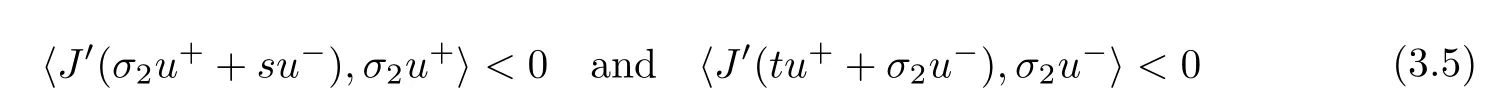
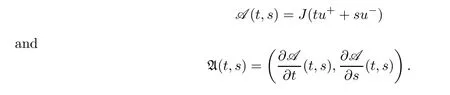




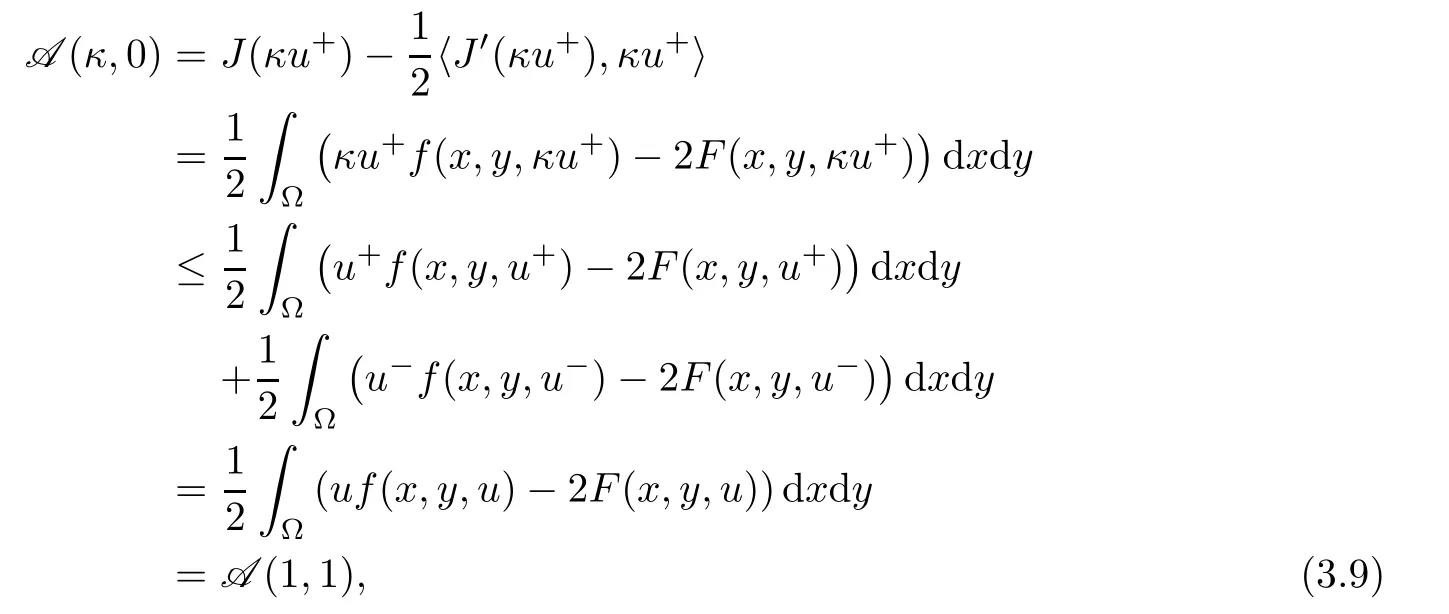






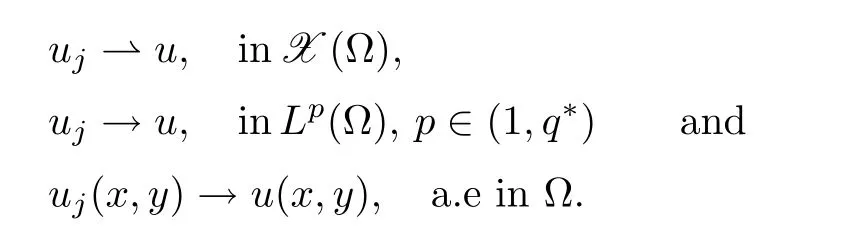
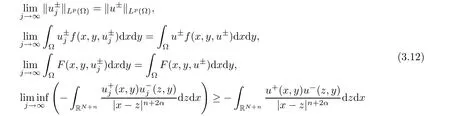
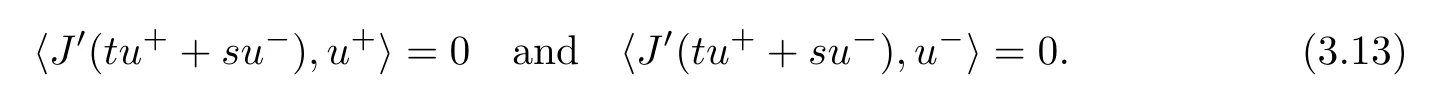







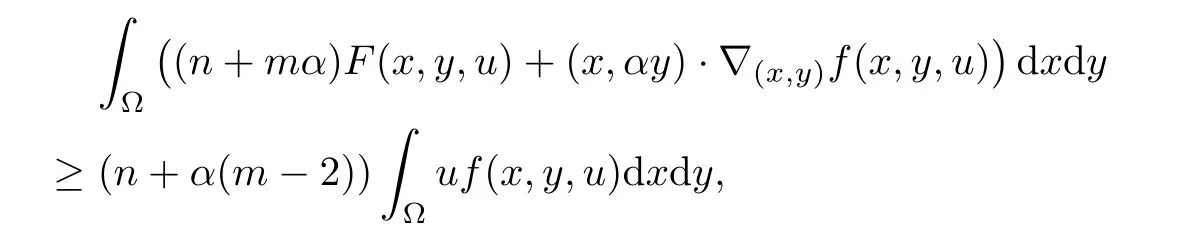
 Acta Mathematica Scientia(English Series)2018年4期
Acta Mathematica Scientia(English Series)2018年4期
