钙钛矿型氧化物非常规铁电研究进展∗

赵国栋 杨亚利 任伟

(上海大学理学院物理系,上海大学材料基因组工程研究院,上海大学量子与分子结构国际中心,上海市高温超导重点实验室,上海 200444)

(2018年5月10日收到;2018年6月6日收到修改稿)

1 引 言

晶体和薄膜铁电材料可用于制作压电、光伏、信息存储和换能传感等电子器件[1,2],而对于铁电性的研究也拓宽了人们对对称性破缺等基本效应的认知,促进了新奇物相与相关物理机制的研究进程[3−8].铁电与铁磁两种铁性有序共存的磁电耦合多铁材料近年来一直备受关注,因其具有磁电耦合效应有望实现基于电控磁的低功耗电子器件[9,10],甚至对利用凝聚态物质对高能粒子物理与宇宙学的理解也有潜在的启示和帮助[11].然而,能够在实际应用中取得颠覆性突破的材料并未被真正开发出来,与磁性产生较强耦合的铁电极化是关键因素[12],设计筛选这类功能材料也是一个非常复杂的问题[13−15].国内外的研究者们一直在努力寻找具有强磁电耦合的材料,最好是电生磁、磁生电或者磁电共生.研究表明,在类似PbTiO3的传统常规铁电体中寻找电生磁需要满足苛刻的条件[16],而著名的铁酸铋BiFeO3多铁材料中电和磁由不同的金属元素相对独立产生.在非常规铁电(improper ferroelectrics)的铁电相变中,铁电极化P(polarization)不再是自发产生的序参量,而是由氧八面体反铁畸变组合、自旋有序或电荷有序诱导的次级参量,因此使得磁生电或电磁共生更为可能.其实多铁材料中根据铁电性的起源不同有很多种分类方法,更多非常详细的介绍可以参考综述文献[17]的总结.

Landau在1937年提出相变唯象理论之后[18],Ginzburg[19−21]首先将Landau相变理论应用在了铁电理论中,而Devonshire[22−24]也独立为Ba-TiO3的铁电性物理发展了与Landau相变理论类似的唯象理论,并拓宽了这种理论使之应用到一级相变.因此,目前在铁电研究中常用的唯象理论被称为Landau-Ginzburg-Devonshire theory,简称LGD理论.在Rabe,Ahn和Triscone[25]编写的铁电物理学专著中,Chandra和Littlewood对LGD理论做了深入浅出的讲解.通常,铁电体可在铁电态与顺电态之间发生一级相变,其特征是在转变温度之下饱和极化强度发生不连续变化.考虑将其自由能密度F作为极化强度P的函数级数展开,即可得到铁电行为的一个热力学形式表述.对于存在铁电态的材料,我们假定函数的级数展开系数a,b,c等只有a=a0(T−T0)线性地依赖于温度,略去高次项之后展开式可简化写为

式中E是外加电场强度(electric f i eld).一般铁电体的顺电相是空间结构反演对称的,它们不会有极化强度P的奇次幂项.热平衡之下,通过F对P的偏导可找到F的极小值,得到自发极化强度(spontaneous polarization).a0和c对铁电体来说都为正数,则T−T0的正负将决定非极化的顺电体是否稳定相变为极化的铁电体.当b>0时,自发极化强度通过转变温度时会随着温度上升连续变为零,发生二级相变;当b<0时,转变温度附近自发极化强度随着温度上升不连续地跳变到零,发生一级相变[26].

1974年,前苏联的研究者基于朗道的相变唯象理论发表了一篇重要综述[27],该综述详细阐述了非常规铁电的定义与特点,将预测的结果与实验结果进行了比较,并指出Indenbom早在1960年就首先理论预测了非常规铁电相变的存在[28].除了铁电极化并非主导驱动的序参量之外,非常规铁电的介电异常现象与一般的铁电材料也有很大不同,如介电常数对温度的依赖关系不遵守居里-外斯定律(Curie-Weiss law),又如电场无法抑制相变等.非常规铁电的畴结构也具有很特别的性质,它存在极化相同的畴结构,这是因为非常规铁电相变发生时的失稳并非对应于铁电极化.需要注意的是,在某个体系中,若有物理量与极化有线性关系(在相变中同阶出现),而又因为其他的特定考虑将之选为了序参量,那么这种体系不能被归类为非常规铁电:如磷酸二氢钾中选为序参量的阳离子序[27].1973年,Holakovsky[29]还提出一种所谓的触发型铁电相变(triggered ferroelectric phase transition),该相变的能量项中包含了触发参量的平方与铁电极化强度的平方之间的双平方项乘积.

2008年之前,除了对YMnO3体系的少量研究工作以外[30],在多铁领域关注钙钛矿材料中由反铁畸变产生非常规铁电的尚不多见[14,31],即使在2009年Khomskii[32]的综述中,也只是将这一类铁电体描述为“几何”铁电体而并非“非常规”铁电体.当时的主要关注点还是由自旋产生的非常规铁电,如2007年在Cheong和Mostovoy撰写的综述中便特别强调了磁阻挫的非公度自旋有序通过逆Dzyaloshinsky-Moriya(DM)相互作用[33,34]产生铁电性的机理[35].2006年,Sergienko等[36]发现自旋zigzag链结构的E型反铁磁正交钙钛矿锰氧化物和镍酸盐中会出现铁电极化,预测这种与自旋轨道耦合无关的E型反铁磁-铁电产生机制可以产生比类似TbMnO3的自旋螺旋有序铁电极化大两个数量级的铁电极化.人们通过求解微观自旋模型、第一性原理计算结合紧束缚近似研究了系列正交钙钛矿锰氧化物的磁性相图,以及随着稀土离子半径变化而呈现出的丰富物性[37,38].自旋排布结构产生非常规铁电的优点是磁控电易,而缺点则是电控磁难[35];即使是在可能比螺旋磁有序产生更大铁电极化的共线磁有序中,由磁生电的极化强度量级也很小[36,39];同时还有重要的一点就是磁阻挫行为往往是发生在低温条件下的.机制类似于YMnO3但晶体结构却不相同的六角钙钛矿2H-BaMnO3[40]在低温条件下也可以出现反铁磁和非常规铁电极化.另外Park等[41]在2017年的研究发现,在电荷有序的短周期LaVO3/SrVO3钙钛矿超晶格中,通过调控三价和四价状态的钒离子可以存在的一个亚稳态拥有很大的极化强度.稀土锰氧化物RMn2O5磁阻挫多铁体系中的磁电耦合效应也受到了国内外学者的广泛关注[42−48].

2008年,Bousquet等[49]发表了关于非常规铁电实验和理论研究的开创性工作,他们首次在短周期(short-period)的钙钛矿超晶格PbTiO3/SrTiO3中,发现了因异质结界面相互接近使氧原子大部分处于对称破缺的界面环境下而导致的非常规铁电行为.在该体系中,产生了共存且相互竞争的铁电FEz、反铁畸变AFDzi和AFDzo,他们对应于相互独立的参量和其中铁电畸变不稳定性FEz可被抑制,即极化强度Pz不是驱动的首要序参量.作者根据高对称P4/mmm相结构的声子谱在Γ(0,0,0)和M(1/2,1/2,0)两点出现的虚频,考虑到其存在不稳定模FEz(),AFDzi()和AFDzo().查表知ϕzi,ϕzo的乘积转化为Pz,因此Pz不变量项的最低阶是形如的一阶项.线性耦合项的存在加上实验中发现ϕzi和恰有相同的相变温度,至此非常规铁电性的条件便被满足.体系的朗道自由能展开式可以表达为

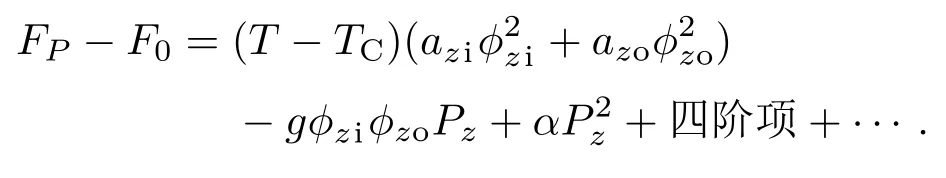
原本纯体态PbTiO3的铁电相变是一级相变,但因为应力与极化强度的耦合作用,实验发现Sr-TiO3在拉伸应变作用之下,PbTiO3/SrTiO3超晶格在任意PbTiO3原胞层数比例下都转变成了铁电二级相变[50].考虑到弹性应变,需在自由能密度的简化展开式中添加应变项.一般来说极化会与一种或多种应变相耦合,而因为对称性的限制,应变与极化的最低阶耦合项可写作ηP2.在弹性应变η与极化P的耦合作用下,压应力能使一个b<0的一级相变会变得更加“一级”(甚至可能使一个二级相变变成一级相变),临界温度T0也会升高.且晶格常数的四方度c/a在此是与平方项P2z耦合,而非长周期超晶格中的线性耦合[51].一般平均场的铁电体满足自发极化强度Ps∝(TC−T)1/2,但在这里的非常规铁电中ϕzi和ϕzo是各自与(TC−T)1/2成正比的序参量,因此从Pz的三线性耦合项可知另外,介电极化率X也不再遵守居里-外斯定律,其数值与温度基本无关,而只在相变点有一个跳变的台阶,这样一个稳定的介电极化率也可能会有潜在的应用价值.这项工作不仅表明了人工超晶格中界面结构的可控性,还指出了其他一些材料中磁性也常与结构畸变有所关联,为人们打开了一个能产生磁电耦合的新思路,引发了在超晶格中利用氧八面体倾转畸变来实现高温磁电耦合的一系列工作.Sai等2009年的研究发现,在非常规铁电薄膜中甚至有希望突破使得铁电极化消失的临界厚度[52,53],进一步增加了人们对非常规铁电体的研究兴趣.

受2008年Bousquet等[49]的超晶格非常规铁电工作启发,Benedek和Fennie[54]于2011年仔细研究了Ruddlesden-Popper层状钙钛矿材料——Ca3Mn2O7,并提出杂化非常规铁电(hybrid Improper ferroelectrics)的概念.Ruddlesden-Popper型氧化物是一种以阳离子为间隔的层状钙钛矿结构[55,56],其中铁电性与磁性可同时由两种对称性不同的氧八面体倾转模式组合而产生的.通过对这一新型材料体系的深度探索,人们希望找到拥有更强磁电耦合效应的材料.2012和2013年相继有文章总结了在杂化非常规铁电体中对于氧转的分析和设计原则[57−59],便于更有目标地去设计类似的新材料.2013年,在金属-有机框架体系中也提出了杂化非常规铁电[60].我们在钙钛矿超晶格中也开展了相关研究,且预测有望在这类新奇体系中实现室温附近的磁电耦合效应[61,62].2014年,我们超越朗道理论的唯象分析方法,创新性地提出了杂化非常规铁电的原子层次上的微观理论解释[63],这将有助于进行更加精准设计的材料开发和应用.2015年,在层状钙钛矿晶体材料的实验中,利物浦大学Pitcher等[64]通过化学元素替代合成并实现了330 K的室温以上的磁电耦合块材(CaySr1−y)1.15Tb1.85Fe2O7.同年,在此类杂化非常规铁电的Ruddlesden-Popper结构中,人们还发现了由于对称性导致的负热膨胀特性[65].2016年,Cheong团队在n=2的Ruddlesden-Popper层状钙钛矿Ca3−xSrxTi2O7结构相界附近发现了伴随复杂氧八面体倾转的八态涡旋-反涡旋对的拓扑缺陷[66].此外,在2017年,Kurushima等[67]通过高分辨电子显微镜技术直接观测到了杂化非常规铁电的带电畴壁,Lee等[68]也利用群论、微观和谱学技术研究了(Ca,Sr)3Ti2O7杂化非常规铁电的反极化序参量和Neel类型带电畴壁.

近年来,很多国内研究小组对非常规铁电的研究也非常活跃.例如浙江大学刘小强和陈湘明等[69]报道了锰掺杂的Ruddlesden-Popper型Ca3(Ti,Mn)2O7陶瓷中的非常规铁电性,实验表明其居里温度高达1000 K以上,并利用第一原理计算揭示了极化翻转的中间过渡正交相结构.他们还研究了Ruddlesden-Popper型Ca3−xSrxTi2O7陶瓷的晶体结构演化与杂化非常规铁电性[70].天津师范大学和天津大学刘卫芳团队[71]在钠离子掺杂体系中观测到了Ca2.94Na0.06Mn2O7杂化非常规铁电体中的交换偏置.华中科技大学陆成亮与南京大学合作者[72]在钛酸锶衬底上利用脉冲激光沉积技术制备了非常规铁电体Ca3Ti2O7外延薄膜,并观测到薄膜面内电滞回线的超低矫顽场.

西安交通大学缑高阳和麻省理工学院李巨等通过第一原理计算预言了Ruddlesden-Popper型钙钛矿硫族化合物Ca3Zr2S7等系列半导体有望成为可见光区室温铁电光伏效应的候选材料[73];缑高阳还与美国西北大学合作者Rondinelli发现A位有序的LaScO3/BiScO3超晶格中出现具有杂化非常规铁电性的“亚铁电相”和常规铁电性的“铁电相”,且在拉伸性外延应变下会发生由“亚铁电相”到“铁电相”的转变[74];另外设计了具有非常规铁电性的A位有序的双钙钛矿(Cs/Rb)SnI3,并研究了其在铁电光伏方面的性质[75].根据对Ruddlesden-Popper钙钛矿卤化物Cs3Sn2I7和Cs3Sn2Br7的研究,浙江大学王杰团队[76]发现压缩应变可以与反铁畸变产生较强的耦合,进一步诱发导致非常规铁电极化的出现,从能带计算得出这些化合物有可能被用于铁电光伏太阳能材料.利用理论施加拉伸应变或静水压,他们在BaSnO3/SrSnO3超晶格的带隙和极化调控研究上做出了类似的用作光伏材料的预言[77].通过对钙钛矿容忍因子和电子能带的定量计算,进一步揭示了Ruddlesden-Popper钙钛矿硫族化合物Ca3Hf2Se7和Ca3Zr2Se7的铁电性可能更加有利于高效率光伏应用[78].通常情况下量子涨落会完全抑制先兆铁电体的铁电相变,由两种先兆铁电体钙钛矿组成的(SrZrO3)m/(BaZrO3)n层状超晶格,也发现了非常相似的杂化非常规铁电性整数定则[63,79],并且总极化强度可以被拉伸应变进一步增大.清华大学朱静院士团队[80]在非常规多铁体单晶YMnO3中利用透射电子显微镜中的电子束研究了涡旋畴和带电畴壁的动力学演化;清华大学朱静和段文晖院士将球差矫正电镜实验和密度泛函理论计算结合报道了YMnO3六角多铁材料中氧空位缺陷可被用于调控表面重构及其磁电功能性质[81].华南师范大学曾敏团队[82]成功制备了外延生长的六角YMnO3薄膜并观测到了20 nm量级的铁电涡旋畴.南京大学刘俊明团队利用唯象理论研究了六角锰氧化物RMnO3涡旋和反涡旋拓扑畴结构的空间各向异性[83],并利用相场模拟研究了外电场驱动下实空间中拓扑畴结构的动力学演化[84].最近他们还给出了六角锰氧化物YMnO3中的两个序参量对温度和电场的依赖关系,提出从高温P63/mmc到极化P63cm结构的相变[85].东南大学董帅团队[86]通过研究不同A位原子有序排列的Y0.5La0.5TiO3化合物,发现其基态结构中钛离子具有铁磁性,其中一些构型可以出现杂化非常规铁电性以及磁电多铁性质,如果A位无序排列则有可能出现弛豫铁电行为.他们预言了铁硒化合物BaFe2Se3是一种磁性诱发亚铁电材料,比其能量略高的全铁电状态将出现较大的铁电极化.铁原子的块状反铁磁结构通过交换收缩的机制可以产生临界温度很高的铁电性[87].2011年,董帅和刘俊明团队合作[88]实验报道了CaMn7O12是一种由磁性产生铁电性的多铁材料;2012年,向红军和董帅团队合作[89]理论计算解释了CaMn7O12由Dzyaloshinskii-Moria(DM)作用与交换收缩作用共同产生的巨大铁电极化.昆明理工大学代建清[90]利用第一原理计算发现了螺旋磁有序结构CaMn7O12中Mn3位的磁矩方向对非常规铁电性的翻转作用.2011年,复旦大学向红军团队提出了一种自旋螺旋序在三角形晶格反铁磁体中诱发铁电极化的普适理论,随后发展了包含电子和离子贡献的自旋导致铁电极化模型[91,92],在中心反演对称空间结构体系中引入反演中心和元素替换,实现了微观上设计出若干非常规铁电材料的新策略[93].对于几个晶胞厚度的二维钙钛矿氧化物薄膜,他们发现了B位离子二级Jahn-Teller效应导致的[110]方向常规铁电,表面效应导致的[100]方向铁电,和[110]方向上的杂化非常规铁电极化,有趣的是后两种铁电极化态随着薄膜的厚度降低不会消失反而会增强[94].复旦大学向红军、龚新高团队[95]综述回顾了自旋有序产生铁电性的微观原理,其中包括Katsura-Nagaosa-Balatsky(KNB)自旋流模型、键极化模型、逆DM作用模型、交换收缩模型等,并且提出了一个统一的铁电理论模型.中山大学郑跃团队综述总结了包括非常规铁电材料的铁磁、铁电和多铁体中涡旋结构的特点和可控性[96].华东师范大学段纯刚团队[97]发表的综述强调总结了在多铁与磁电耦合研究中第一性原理的应用.南京大学万贤纲与段纯刚团队[98]提出一种非阻挫的磁致铁电机制,即简单的原子间短程磁交换作用可以驱动铁电性.中国科学院物理研究所孙阳团队[99]研究了Y型六角铁氧体BaSrZnMgFe12O22螺旋磁有序下的磁电耦合效应,发现其多铁畴壁钉扎作用导致了一种反常的磁电记忆效应,低温下其铁电态可通过降低外磁场而部分恢复.

本文接下来分为以下三个部分:首先具体介绍最近在钙钛矿超晶格结构及双钙钛矿结构中诱导出的非常规铁电;然后详细讨论在钙钛矿单晶(SmFeO3)块体结构中利用反铁磁畴壁诱导出非常规铁电;最后给出结论和展望.

2 超晶格结构诱导非常规铁电

2008年,Bousquet等[49]基于钙钛矿氧化物普遍拥有氧八面体的倾转畸变这一特性,实验上成功合成了非常短周期的PbTiO3/SrTiO3(铁电/顺电)超晶格结构,这一超晶格结构形成了一种新的界面耦合,诱导了非常规铁电的产生.自此,这种原子尺度界面工程的研究方法便被广泛应用于人工合成铁电极化材料的研究,为探索更多此类具有某些独特性质的多铁物质提供了创新的思路和途径.随后Benedek和Fennie[54]在这一实验的基础上提出了一种电极化与磁化耦合的新概念——杂化非常规铁电.随后的研究表明,这些人工合成的钙钛矿超晶格结构突破了传统铁电材料产生极化所需要的d0规则或长程ns2电子对的限制[15],在阳离子d或f轨道电子非零占据的情况下也能产生此种杂化非常规铁电[57,58].究其实质,杂化非常规铁电起源于一个复杂的晶格结构畸变模式组合,该畸变模式组合由不同对称性的氧八面体旋转组成,产生一个PQ1Q2的三线性项耦合.这里P为电极化;Q1和Q2为两种非极化模式,分别代表普遍存在于钙钛矿中的氧八面体同相(Q1)和反相(Q2)倾转矢量.这一解释可以基于经典的朗道理论,从包含宏观序参量的对称参数中推导而得出的三线性项耦合能量.此外,如图1所示,以上述钙钛矿超晶格结构中的杂化非常规铁电为研究对象,Zhao等[63]最近在晶胞尺度上利用解析推导和图分析方法,从材料中基本的原子间相互作用——亦即氧八面体倾转与A位阳离子位移畸变的三线性项耦合的角度解释了杂化非常规铁电的产生机理.有别于此前基于对称性的朗道理论解释,这一微观理论方法使我们能更深刻也更简单直观地理解杂化非常规铁电,尤为重要的是能解释氧八面体旋转、反铁电位移和阳离子有序在杂化非常规铁电中的作用,以至于构建体系的有效哈密顿量.通过直接的分析推导和相应的图形分析,他们首先证明了此前由Bellaiche和Íñiguez提出的在氧八面体旋转和A位阳离子位移间存在的原子间耦合能量和[100]可以解释层状钙钛矿超晶格结构中的杂化非常规铁电.其次,该方法能便捷地处理沿不同方向(例如[001]或[111])和不同晶胞厚度堆叠的钙钛矿超晶格结构.我们可以很容易地解释为何具有a−a−c+氧八面体旋转[101]并沿[110]方向生长的层状钙钛矿超晶格结构并不能产生非常规铁电,与之前Young和Rondinelli[58]提出的结论相一致.由于该方法的普遍性,为预测先前在中其他类型的杂化非常规铁电提供了可能.我们进一步利用该方法成功展示了在超晶格结构中杂化非常规铁电极化强度P随着层数n及层数m的变化而呈现出的正比于1/(n+m)的定量化数学表达式.图1展示了超晶格结构中杂化非常规铁电产生与否以及非零与否所遵循的规则,当n与m均为偶数时,体系呈现P21/c空间群对称性,无极化生成;当n与m均为奇数时,体系呈现Pmc21对称性,有沿着赝立方[110]方向的极化生成;当n与m满足不同的奇偶性时,体系呈现Pbnm对称性,无极化生成.

从实际应用的角度而言,寻找能在室温或高温下具有电极化和铁磁有序的单相材料是目前极为重要的一个研究方向,然而高温条件下多铁序参量共存和耦合的实现仍面临很大挑战[12,15,102−104].对此,Ležaić和Spaldin[102]基于密度泛函理论计算预测了Bi2MnReO6和Bi2NiReO6在室温下可能呈现铁电极化态,又因为Re和Ni/Mn子晶格都为反铁磁序,所以其整体在室温附近可为亚铁磁态.类似情况还有诸如GaFeO3的外延生长薄膜、六角LuFeO3薄膜、由PbZr0.5Ta0.5O3(PZT)和PbFe0.5Ta0.5O3(PFT)组成的固溶体PZTFT以及LiNbO3型的Zn2FeOsO6[104−107]等. 早在2005年,Azuma等[108]成功合成了具有岩盐结构的Bi2NiMnO6双钙钛矿结构,其铁电和铁磁序产生的临界温度分别为485 K和140 K.虽然485 K的临界铁电温度能满足室温条件,但140 K的铁磁序温度却使其无法满足实际应用.尽管如此,Azuma等的研究结果为发现在室温下同时存在铁电和铁磁的其他双钙钛矿结构提供了借鉴和依据.2004年,Bull和McMillan[109]通过拉曼光谱对稀土双钙钛矿结构R2CoMnO6和R2NiMnO6(R为稀土元素,La,Sm等)进行了比较系统的研究.他们发现此双钙钛矿结构在居里温度(TC)下均为铁磁序,且随着R离子半径减小也线性减小,其中La2NiMnO6的临界铁磁序温度高达287 K,Pr2NiMnO6也达到255 K,然而,此双钙钛矿结构并不呈现极化.通过对结构的仔细研究可以发现,R2NiMnO6具有与a−a−c+氧八面体旋转[101]伴随出现的反铁电位移,结合之前对沿(001)方向生长的超晶格结构存在杂化非常规铁电的研究,Zhao等[61]基于第一性原理实现了对沿(001)方向生长的R2NiMnO6/La2NiMnO6双钙钛矿超晶格结构的理论设计(如图2所示)及对其杂化非常规铁电与磁有序的研究.由于镧系稀土离子半径的尺寸存在差别,我们可以充分利用这一化学压强效应,并结合金属氧化物外延生长技术实现的晶格应变来调控电极化和磁有序结果.图3显示了晶体几何结构和原子全优化的R2NiMnO6/La2NiMnO6超晶格特性随化学压[110,111]的变化关系.图3(a)表明随着化学压逐渐减小,即R3+离子半径减小时,超晶格结构(P21对称性空间群)的极化强度逐渐增大.图3(b)给出了不同化学压条件下超晶格中各离子沿b轴方向所受的平均极化力(沿a,c轴方向无剩余平均极化力),可以看出在所有受力离子中R3+离子所受极化力占主导地位,方向平行于b轴;而且随着R3+离子半径减小,其所受极化力将增大.由此可以得出结论:在结构全优化的情况下,R2NiMnO6/La2NiMnO6超晶格中铁电极化主要来源于稀土R离子和La离子的幅度不同的反向反极化位移.图3(c)和图3(d)分别给出了随R3+离子半径变化时,体系在0 K温度下磁化强度及通过蒙特卡罗模拟的顺磁-铁磁转变居里温度的变化情况.可见随着R3+半径减小体系的磁化强度微弱地单调增大,相对应的顺磁-铁磁转变温度随之降低,其中Ce2NiMnO6/La2NiMnO6的290 K为最高,也令Ce2NiMnO6/La2NiMnO6极有希望成为室温多铁材料.进一步的外延应变计算研究表明,对R2CoMnO6和R2NiMnO6超晶格结构施加面内双轴应变时,体系的极化大小不会呈现大的变化,而顺磁-铁磁转变温度将有一个小幅度的涨落,其中Ce2NiMnO6/La2NiMnO6的顺磁-铁磁转变温度将在其面内赝立方晶格常数处于3.70—3.80 Å范围内时出现在290 K附近.

图1 [001]方向生长的及超晶格结构中导致杂化非常规铁电的反铁电位移,其中与均具有a−a−c+氧八面体倾转模式 (a)显示了中[110]方向的反铁电位移,阳离子A′与A′′的相反方向位移(用长度不同的有色箭头表示)未能完全抵消,致使生成杂化非常规铁电;(b)当n与m都为偶数时,超晶格结构相邻A′O层或相邻A′′O层方向位移相互抵消,不产生极化;(c)表示了一个特例,即当n与m同为奇数时, 超晶格结构产生杂化非常规铁电;(d)表示当n与m满足不同奇偶性时,超晶格结构不可产生非零的极化;(e)表示不同的n与m整数组合条件下,沿[001]方向生长的(LaFeO3)m/(YFeO3)m超晶格结构中非常规铁电极化强度幅度与稀土阳离子成分的关系[63]Fig.1.Sketches of the antipolar displacements leading to hybrid improper ferroelectricity in theandsuperlattice grown along[001]direction with bothandhaving an a−a−c+tilting pattern.Panel(a)shows the antipolar displacement in the case of thealong[110]direction.The lack of full compensation between the motions of theandatom(represented by arrows of dif f erent lengths)leads to hybrid improper ferroelectrics.Panel(b)corresponds to the case when both n and m are even and shows that no polarization exist since antipolar motions precisely cancel each other in the A′O and A′′O layers.Panel(c)shows the unique case in which hybrid improper ferroelectrics can occur,that is when n and m are both odd.Panel(d)represents the case when n and m are of dif f erent parity,which also results in a vanishing polarization.Panel(e)provides the magnitude of the polarization of(001)(LaFeO3)m/(YFeO3)msuperlattices as a function of lanthanide composition for dif f erent combinations of n and m[63].

图2 R2NiMnO6/La2NiMnO6超晶格P21基态结构 (a),(b)分别为晶体的三维视图和顶视图;La3+,R3+,Ni2+,Mn4+及O2−等离子分别用绿色、橙色、蓝绿色、紫色及红色球表示;NiO6和MnO6分别用蓝绿色和紫色八面体表示;沿b轴方向,相对于La3+离子的反铁电位移矢量离子的反铁电位移δ2大小不同,这一非均匀性即是铁电极化产生的微观原因;此外RO平面内R3+沿a轴方向的反铁电位移可用+δ3和−δ3表示[61]Fig.2.P21ground state of the studied R2NiMnO6/La2NiMnO6superlattices.(a)Representation in three dimensions.(b)Representation in the(a,b)plane.The La3+,R3+,Ni2+,Mn4+and O2−ions are displayed as green,orange,cyan,purple and red spheres,respectively.The NiO6and MnO6octahedra are displayed using cyan and purple octahedra,respectively.The largest magnitude of the antipolar displacement(δ2)of the R3+ions with respect to those(δ1)of the La3+ions along the b axis is schematized here to emphasize that this inhomogeneity is the microscopic reason for the creation of the electrical polarization.The antipolar displacements along the a axis of the R ions within the RO plane(denoted as+δ3and −δ3)[61].

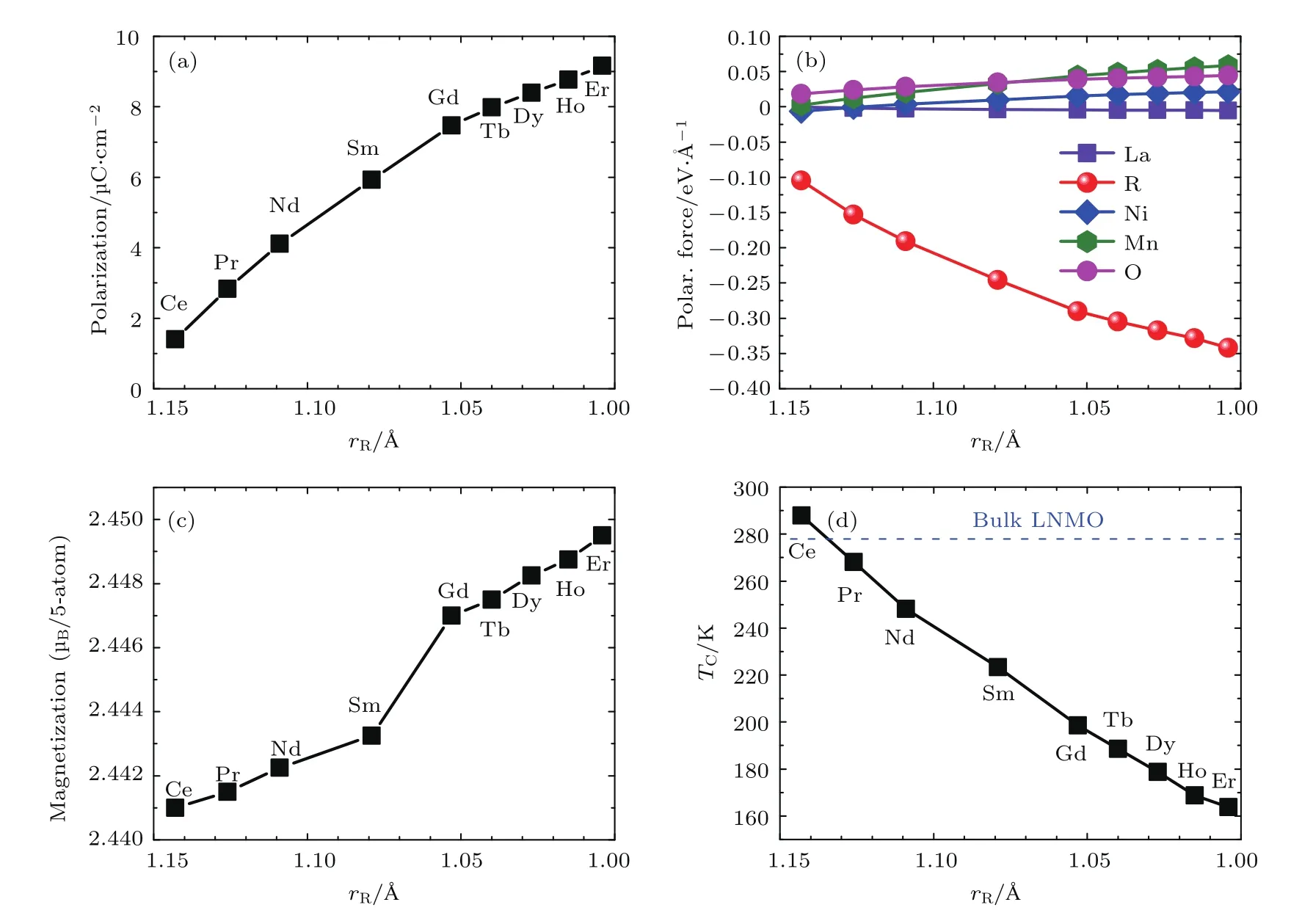
图3 稀土离子半径变化时R2NiMnO6/La2NiMnO6超晶格结构性质 (a),(c),(d)分别为全优化条件下R2NiMnO6/La2NiMnO6超晶格处于P21基态时所预测的电极化强度(基于Berry phase计算)、磁化强度(T=0 K)和顺磁-铁磁转变温度(基于蒙特卡罗模拟);(b)未优化条件下R2NiMnO6/La2NiMnO6超晶格中La3+,R3+,Ni2+,Mn4+及O2−离子沿b方向所受的平均力;此时的晶格常数为La2NiMnO6处于P21/n顺电态时的晶格常数;(d)中绿色水平虚线代表体相La2NiMnO6的磁居里温度[110,111]Fig.3.Properties of R2NiMnO6/La2NiMnO6systems as a function of the rare-earth ionic radius[110,111]:(a),(c),(d)The predicted electric polarization(as computed from Berry phase),magnetization(at T=0 K)and paramagnetic-to-ferromagnetic transition temperature(as calculated by Monte Carlo simulation)in the relaxed P21ground state of the superlattices,respectively;(b)the average forces(along the b direction)on La3+,R3+,Ni2+,Mn4+and O2−ions in the unrelaxed state of the R2NiMnO6/La2NiMnO6superlattice,for which the lattice parameters and atomic coordinates are those of the paraelectric P21/n state of La2NiMnO6and for which the R ions occupy the second AO layer of Fig.1(a);the blue horizontal dashed line in(d)represents the magnetic Curie temperature of La2NiMnO6bulk.

3 反相磁畴壁诱导非常规铁电

稀土铁氧体RFeO3和稀土铬氧体RCrO3(R为稀土元素)拥有钙钛矿材料中最常见的(GdFeO3型)正交结构,晶体空间群为非极性的中心对称结构Pbnm[112,113].然而,最近的理论研究表明[39]在钙钛矿RFeO3,RCrO3结构中,若仅考虑B位(Fe/Cr)的G型反铁磁性而把A位(R)做无磁性处理(即将R元素的4f电子冻结到离子核芯内),则体系呈现中心反演对称性,铁电极化无法产生.若A位(R)和B位(Fe/Cr)同时存在适当的磁结构,则特定的自旋排布将能在ABO3中诱导出非常规铁电.当A,B位均为G型反铁磁排列且相互平行时,体系的极化值最大.图4所示为A,B位磁矩相互平行且分别沿a,b和c三个不同方向排列,体系晶体结构对称性为Pna21,极化沿c方向产生约为−0.4µC/cm2.需要注意的是,在图4中,当A,B位的G型反铁磁沿a轴平行排列时,体系将有朝向c轴的倾角弱铁磁产生;当A,B位G型反铁磁沿c轴平行排列时,倾角产生的弱铁磁朝向负a轴;而当A,B位G型反铁磁沿b轴排列时,体系将无弱铁磁生成.由此可知,体系极化畸变的产生并不依赖于体系净磁矩的产生与否.然而我们知道,在稀土铁氧体和稀土铬氧体中,稀土离子呈现自旋有序排列的温度很低[114,115],因此该多铁性将很难运用于实际器件之中.有趣的是,作为稀土正铁氧体家族中的重要一员,有报道称SmFeO3在温度高达670 K以下能呈现铁电序,引起了国际学者的广泛关注,然而其极化生成的机理却存在巨大争论[116−119].近期,基于实验合成制备、物性表征和第一性原理计算,人们发现在Lu2CoMnO3[120−122]和Y2CoMnO3[123]等双钙钛矿结构中B(B′)位离子存在特定的自旋序,该自旋排列引起的磁畴壁能诱导出非常规铁电极化.有别于前文所述超晶格结构产生的杂化非常规铁电,这里非常规铁电的产生得益于自旋特定排列造成的对称性破缺,可归类于所谓的共线磁结构“第二类”多铁材料[32].

图4 稀土钙钛矿中两套磁子晶格产生铁电极化的自旋构型[39] (a),(b),(c)中G型反铁磁矢量的主磁矩分别沿Pbnm结构中的a,b,c轴取向;图中蓝色较大圆球代表稀土离子,青色较小圆球代表过渡金属离子Fig.4.Spin conf i gurations yielding the ferroelectric polarizations are shown for two sublattices of magnetic ions in the rare earth perovskites[39].In(a)–(c)the dominant G-type antiferromagnetic vectors are along a,b and c directions of Pbnm phases,respectively.The bigger blue spheres represent the rare earth,and the smaller cyan spheres represent the transition metal ions.

图5 铁酸钐晶体SmFeO3中X0磁单畴和几种Xn-m磁畴内Fe3+自旋排布示意图[124](a)G型反铁磁;(b)C型反铁磁;(c)A型反铁磁;(d)F铁磁构型;绿色平面代表磁畴壁处,畴结构中的蓝色和红色箭头分别表示自旋向上和自旋向下Fig.5.Schematic of the Fe3+spin arrangement in the studied X0magnetic monodomains and some Xn-m multidomains of SmFeO3for(a)G,(b)C,(c)A,and(d)F.The green planes locate the domain walls,while blue and red arrows represent spin up and spin down,respectively[124].

Yang等[124]最近基于第一性原理和模型计算,在体相SmFeO3中利用不同种类的特定自旋序构造了人工磁畴结构.我们在此不考虑任何相对论效应及自旋轨道耦合,仅利用简单的共线磁序排布构造出沿(001)方向的反铁磁畴壁.如图5所示,X0为四种磁单畴结构G0,C0,A0和F0(X=G型反铁磁,C型反铁磁,A型反铁磁,F铁磁构型);Xnm表示其磁畴结构,n和m为每个磁畴中所包含的FeO2层数,而相邻的磁畴则组合成反相畴界.在考虑结构弛豫时,一方面我们先将晶格常数固定为实验报道的数值去优化原子位置,可得如图6的铁电极化强度与n和m的依赖关系图,图6(a)—(d)分别对应于Gn-m,Cn-m,An-m反铁磁畴壁和Fnm铁磁畴壁结构.对单畴结构X0而言,反铁磁和铁磁四种类型自旋排布结构的晶体均为Pbnm对称性,不可生成铁电极化.对畴壁结构Xn-m而言,当n和m相等且均为奇数时,体系依旧是Pbnm对称性,不生成极化;当n=m且均为奇数时,体系变为P21/c对称性,但不生成极化;当n和m均为偶数时,体系将变为Pmc21对称性,有沿b方向的极化生成,而且体系的总极化值随n和m之和的值的增大而逐渐减小.这一点很容易理解,因为同取向畴的体积变大而畴壁的密度降低导致铁电极化应当在趋于无畴壁的极限下趋于零.有趣的是图6中铁电极化计算值的量级大小和方向(b轴方向)与实验观测比较一致[116].通过对Xn-m畴结构进行离子平均位移分析得知(如图7),体系内所有原子沿b方向均有位移(沿a,c方向也有位移但无净位移剩余,这与体系沿a,c方向无极化生成相一致),特别是处于反铁磁畴壁处的O2−离子具有比其余离子大得多的位移.然而,对n和m均为奇数的磁畴体系而言,其相邻反铁磁畴壁处O2−离子位移相互抵消,无净位移剩余;对n和m均为偶数的体系而言,其相邻反铁磁畴壁处位移朝向相同,有净位移剩余,生成与净位移方向相反的铁电极化.进一步的理论模型分析表明此非常规铁电的生成机理为磁致交换伸缩效应导致在反铁磁畴壁处O2−离子位移不能相互抵消,存在界面上的电偶极矩.另一方面,我们也对以上结构进行了全优化,计算结果表明尽管与固定晶格常数的结果在定量上有些许差异,但定性上两者的结论完全一致.最后,通过对多种RFeO3和RCrO3的计算表明,我们人工构造的反铁磁畴壁均能在相应体系中普遍地诱导出非常规铁电.

图6 铁电极化的理论计算值与(a)Gn-m,(b)Cn-m,(c)An-m,(d)Fn-m磁畴构型中的n和m组合对应关系图[124]Fig.6.Computed magnitude of the electrical polarization for the various studied combinations of n and m in the(a)Gn-m,(b)Cn-m,(c)An-m,and(d)Fn-m structures[124].

图7 奇偶性不同层数的反铁磁畴壁(绿色线)处氧离子的位移方向(黑色箭头)[124] (a)构型G3-3的两个磁畴中分别包含3层铁氧面;(b)构型G4-4的两个磁畴中分别包含4层铁氧面Fig.7.Displacements of oxygen ions(represented by black arrows)located at domain walls(represented by green lines)in the(a)G3-3 and(b)G4-4 spin confi gurations which contain 3 FeO2planes and 4 FeO2 planes in each domain,respectively[124].

4 结 论

本综述系统性地回顾了非常规铁电的最新进展,根据近期的研究实例详细介绍了在钙钛矿氧化物中诱导非常规铁电的几种不同途径,并对其理论机制进行了阐述.通过对原子尺度层次超晶格结构的构造,利用不同元素离子半径不同的特点可以成功设计出非常规铁电,而且能够突破传统规则的限制使得磁性和铁电性共存,实现钙钛矿氧化物的多铁性.磁电耦合类多铁材料方面还可以利用对双钙钛矿结构的有序排列,寻找出更多具有室温磁序与极化共存的复杂氧化物材料.又或者不同于常规的第一类多铁材料,通过人工构造特定磁结构(例如反铁磁畴壁)产生对铁电极化的诱导,从而实现非常规的第二类多铁材料.我们希望此综述能增进人们对非常规铁电材料以及与之紧密相关的诱导磁电耦合、调控手段方面的系统理解,以促进实验与理论计算研究的结合,探索更多诱导铁电性与多铁耦合材料的新物理.