土壤含水量增墒、退墒预测模型的研建与应用

邹文安 ，吕守贵

（1. 吉林省水文水资源局，吉林 长春 130022；2. 吉林省水文水资源局通化分局，吉林 通化 134000）

0 引言

近年来，由于国内局地性、区域性干旱灾害频繁发生，对墒情信息的时效性要求越来越高，常规的墒情监测频次难以满足抗旱工作需求，探索土壤墒情测报方式改革创新，是各省（区、市）面临的重要课题。由于我国墒情自动测报系统建设起步较晚，土壤含水量监测精度不高，田间持水量成果不可靠，导致墒情自动监测信息尚未全面投入生产实际应用，国内各省（区、市）墒情测报仍以人工烘干称量法监测为主。该法存在监测周期长、成本高、时效性差等弊端。尤其当作物关键生长发育期、旱情发展严峻期间和前期干旱少雨发生有效降雨时，旱情发展变化快，应进行墒情加测、加报，才能满足抗旱减灾工作需求。开展高频次的人工墒情测报，会给墒情监测工作带来巨大的压力。

土壤含水量预测可以解决人工监测存在的问题。国内常见的土壤含水量预测有以下 5 种方法[1]：1）退水曲线法。耕作层土壤含水量一般呈稳定的消退规律，能够用线性关系式表达。2）前后期土壤含水量相关法。通过建立前期土壤含水量与后期土壤含水量相关关系，预测后期土壤含水量。3）水量平衡法。在某种水量平衡系统中，土壤含水量与降水量、蒸散量等要素关系密切，通过水文要素关系转换，可以建立土壤含水量与其它要素某种函数或相关关系，以此预测后期土壤含水量。4）回归分析预测法。根据水文要素之间的相互作用、影响，找出这些因素之间的统计规律，并选用合适的数学方程式加以描述。5）预测模型法。通过预测模型建立起待预测水文要素变量和各影响因子状态之间的对应关系，进而实现该水文要素变量的状态预测。

目前，我国土壤含水量预测理论不够完善，预测技术方法还处于研究探索阶段，许多研究成果尚未推广应用。2000 年，清华大学雷志栋、尚松浩等利用土壤水分变化率与贮水量成正比这一规律，基于土壤水分的消退指数建立了冬小麦生育期土壤墒情预报的经验递推及 BP 神经网络预测等模型；2002 年，河海大学蒋洪庚、夏自强等运用平原水文模型，通过土层蓄水量与土壤墒情之间关系的研究，构建了区域土壤墒情预测模型；2006 年，黑龙江省水科学研究院李芳花等采用“3S”技术，以墒情遥感与土壤水分消退蒸散等模型为核心，综合利用极轨气象卫星的遥感数据源与多点地面监测墒情、气象观测数据，研发了黑龙江省墒情信息管理系统[2]。2016 年，安徽省、吉林省和宁夏自治区的水文部门根据本省（区）实际，利用区域水量平衡原理，建立了区域土壤含水量预测模型[3]，预测成果已应用到墒情评价、旱情分析及 Web 平台墒情信息服务系统中，为地方各级政府指挥抗旱减灾提供了可靠的决策依据。

本研究着重介绍水量平衡法土壤含水量预测模型创建及应用。

1 预测理论依据分析

杨志峰、崔宝山等[4]认为，在天然旱地植被系统中，“四水”（大气水、地表水、土壤水和地下水）水量平衡存在以下关系：

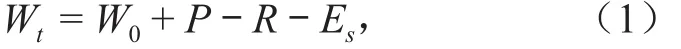
式中：Wt为时段末期土壤含水量；W0为时段初期土壤含水量；P，R 分别为时段内降水量及总产流量；Es为时段内土壤蒸散发量、作物蒸腾量。

如果监测时段内不发生降水，则不会产生径流，即 P = 0，R = 0，这时式（1）转换为 Wt= W0-Es。当蒸散量 Es较稳定时，末期土壤含水量与连续无雨日数 ts有关，于是时段末期土壤含水量 Wt函数表达为

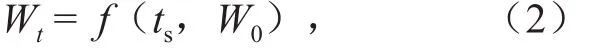
式（2）表明，时段末期土壤含水量 Wt与时段初期土壤含水量 W0、连续无雨日数 ts有关。

通过转换，可得到 Wt- W0= P - R - Es，其中Wt- W0为土壤含水量的变化量/增量，可用 ∆W 表示，则 ∆W = P - R - Es。该式表明，土壤含水量增量 ∆W 与降水量 P、产流量 R 和蒸散量 Es有关。由于区域产流量 R、蒸散发量 Es不易实测，无法具体量化表示，其影响作用可作为非量化处理，于是土壤含水量增量 ∆W 函数可表达为

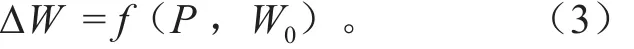
式（3）为天然旱地植被系统中，土壤含水量增量函数表达式。

2 预测模型建立

选用吉林省西部半干旱平原区的西太平川站、胡家店站 2 个墒情站作为研究对象，对应土壤质地为砂土、壤土，田间持水量分别为 14.8% 和 16.0%。

基本资料包括土壤含水量、降水量、连续无雨日数和田间持水量测定等实测资料，其中，胡家店资料系列为 2002—2016 年，西太平川站为 2014—2016 年（新建站）。

2.1 退墒模型建立

以西太平川站为例，阐述退墒模型创建过程。选取该站历史墒情监测资料，整理和统计土壤含水量、田间持水量和连续无雨日数，点绘土壤含水量与连续无雨日数关系图。创建过程如下：

1）数据选用与整理。高水数据退墒采用本站田间持水量测定实验数据，即利用田间持水量测定实验中土壤含水量和累计连续退水时间作为高水退水过程的相关图点距。

中低水部分采用本站历年常规监测成果。筛选出具有连续无雨测次的墒情实测资料，统计各测次土壤含水量及连续无雨日数，以此作为中低水退墒过程的相关图点距。

以西太平川墒情站 2014—2016 年田间持水量测定实验和部分常规墒情监测资料为基本数据，按土壤含水量从大到小依次排列，整理土壤含水量与连续无雨日数对应关系，如表 1 所示。

2）测次间的数据衔接处理。由于自然状态下很少会出现连续几十日无雨的情况，实际统计出来的各测次连续无雨日数是独立的、阶段性的，给点绘退墒曲线带来一定难度。为了保证土壤含水量各量级数据能够连接为一个完整的、连续的退墒过程，本次分析采用按土壤含水量相同量级进行链接处理的方式，即将整理出的相同土壤含水量进行重合叠加，连续无雨日数进行累加的方式处理，实现从高水到低水是完整的、连续的退墒过程，符合土壤水消退规律。

3）退墒曲线绘制。将连续无雨日数与土壤含水量数据录入 Microsoft Excel 工具表，利用工作表中“图表”中的“XY 散点图”绘图功能，以连续无雨日数 ts作为 x 轴，以人工烘干称量法监测的土壤含水量 W 作为 y 轴，点绘各测次 W 与 ts关系图。生成散点图后，根据关系图数据点距及分布情况，确定选择添加趋势线类型并拟合出二者关系式。经分析，西太平川站土壤含水量与累计连续无雨日数趋势线为对数曲线，曲线如图 1 所示。

4）拟合精度检验。为了检验退墒曲线拟合精度，需对参加退墒曲线拟合点距进行精度评定。评定指标为：实测值与退墒模型计算值（预测值）差值的绝对值 ≤ 2%，视为合格[5]，合格率（合格点距个数与参加检验点距总个数的百分比）≥ 80%，检验合格[6]。通过对西太平川墒情站退墒曲线 39 组拟合点距检验，误差均 ＜ 2%，合格率达 100%，表明该站退墒曲线拟合精度较高。

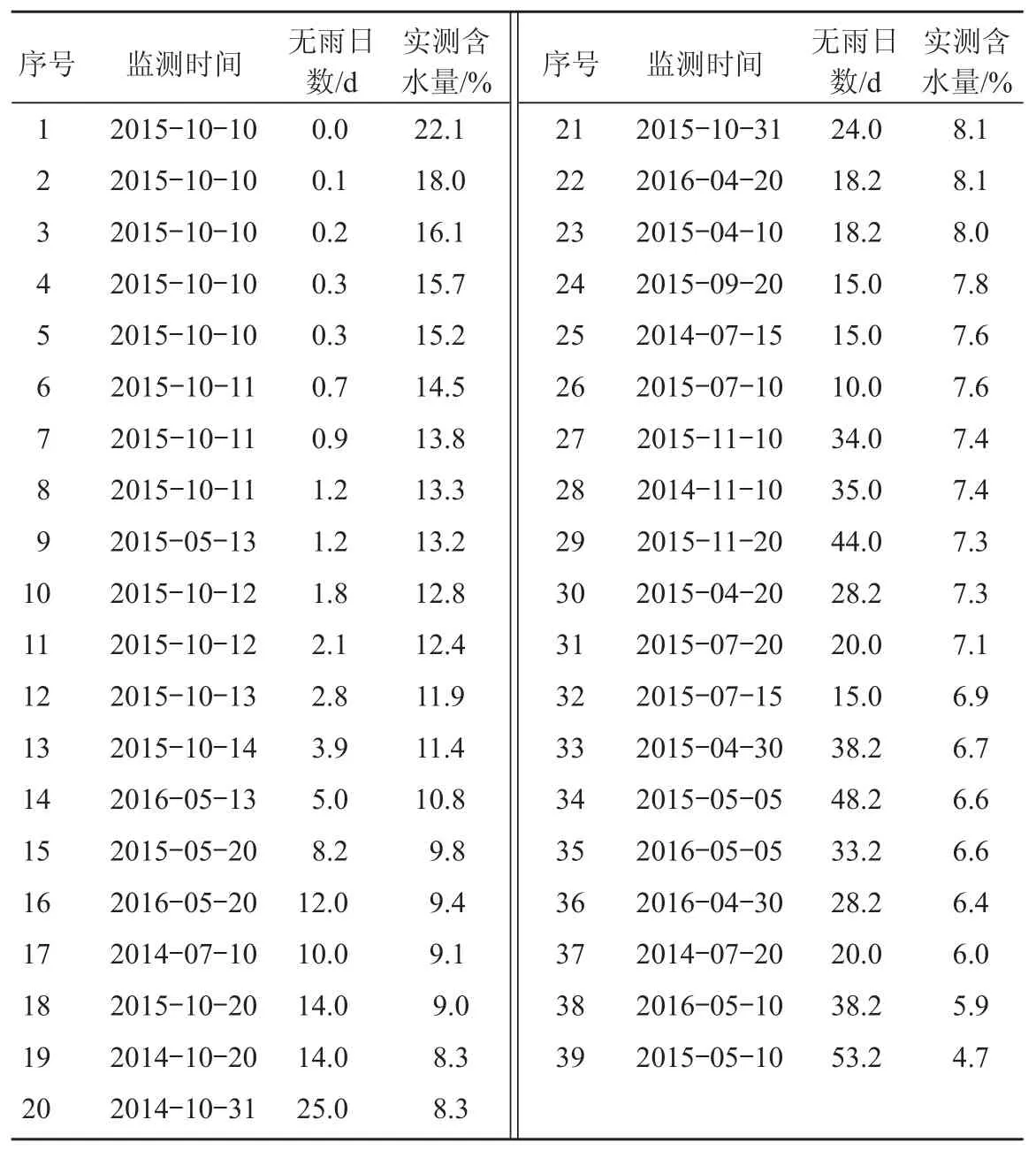
表 1 西太平川站土壤含水量与连续无雨日数对应关系表

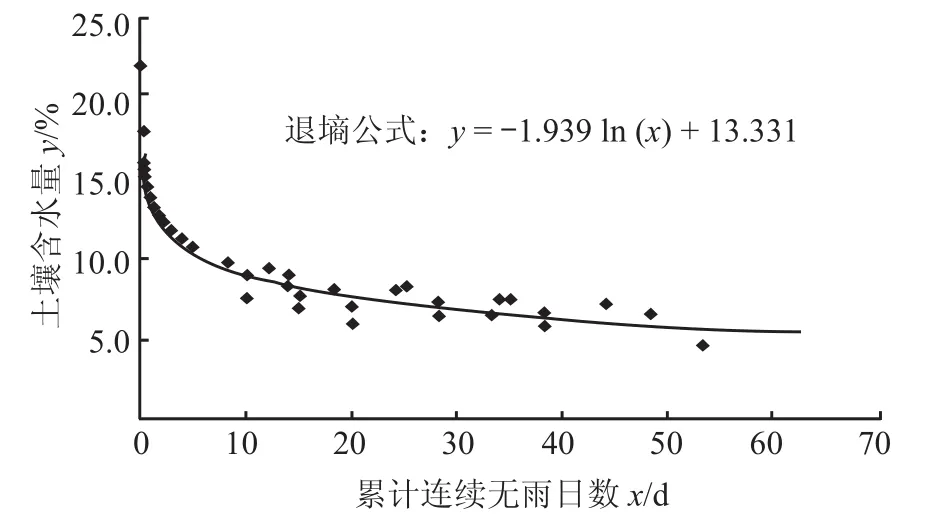
图 1 西太平川站退墒曲线图

5）预测精度检验。选取西太平川墒情站 2014和 2016 年共 15 组实测墒情数据（未参加退墒曲线拟合，前后测次间无有效降水）进行验证。根据前次实测土壤含水量及两测次间连续无雨日数，用退墒公式计算后测次对应土壤含水量（预测值），与后测次实测值进行对比，计算出合格率。

同拟合精度检验一样，预测检验精度按实测值与退墒公式计算值（预测值）差值的绝对值 ≤ 2% 视为合格。经检验，西太平川站退墒预测有 13 组数据合格，合格率为87%，超过规定的 80%，精度满足规定要求，可以应用到生产预测。

2.2 增墒模型建立

以胡家店站为例，阐述增墒模型创建过程。选取该站历史实测墒情资料，进行雨前土壤含水量、雨后土壤含水量（部分数据采用本站退墒模型计算）统计，计算各次土壤含水量增量 ∆W、时段累计降水量P，点绘土壤含水量增量与时段累计降水量相关图，拟合出土壤含水量增量计算关系式。

2.2.1 数据整理及退墒计算

1）资料选用。土壤含水量、降水量采用实测资料，选择时段降水量 ＞10 mm，雨后增墒明显、代表性好的测次。

2）时段降水量计算。根据本站降水日表，摘录、计算测次间对应的时段累计降水量。

3）雨前土壤含水量计算。选用的墒情资料中，如果墒情监测后即开始降雨，则雨前土壤含水量即为雨前实测土壤含水量；如果在墒情监测日后经过一段时间间隔才发生有效降雨，则雨前土壤含水量为雨前实测土壤含水量利用本站退墒模型向后推算到降水前一日的土壤含水量。

4）雨后土壤含水量计算。雨后第 2 日有实测土壤含水量则为雨后土壤含水量；如果雨后第 2 日无实测土壤含水量，那么根据雨后首次实测土壤含水量利用本站退墒模型向前推算到雨后第 2 日土壤含水量，该含水量作为雨后土壤含水量。

2.2.2 土壤含水量增量计算

列表统计雨前土壤含水量、雨后土壤含水量（退墒模型推算值视为实测值）和降水量，计算实测土壤含水量增量，增量等于雨后土壤含水量与雨前土壤含水量之差。

胡家店站土壤含水量增墒曲线拟合精度检验结果显示，参加拟合精度检验的 29 组数据中，27 组检验合格，2 组不合格，合格率达 93%，如表 2 所示。

2.2.3 增墒曲线绘制

在 Excel 工具表中利用图表向导中的散点图进行增墒曲线绘制。以累计降水量 P 为自变量（x 坐标），以实测土壤含水量增量 ∆W 为因变量（y 坐标），点绘胡家店站 P 与 ∆W 相关图，如图 2 所示。根据相关图数据点距分布情况添加趋势线，拟合出累计降水量与土壤含水量增量计算公式：当 7.5 ＜P ＜ 67.0 时，土壤含水量增量 ∆W = 2.696 ln (P) -5.418 2；当 P ≥ 67.0 mm 时[7]，∆W = 5.9%。

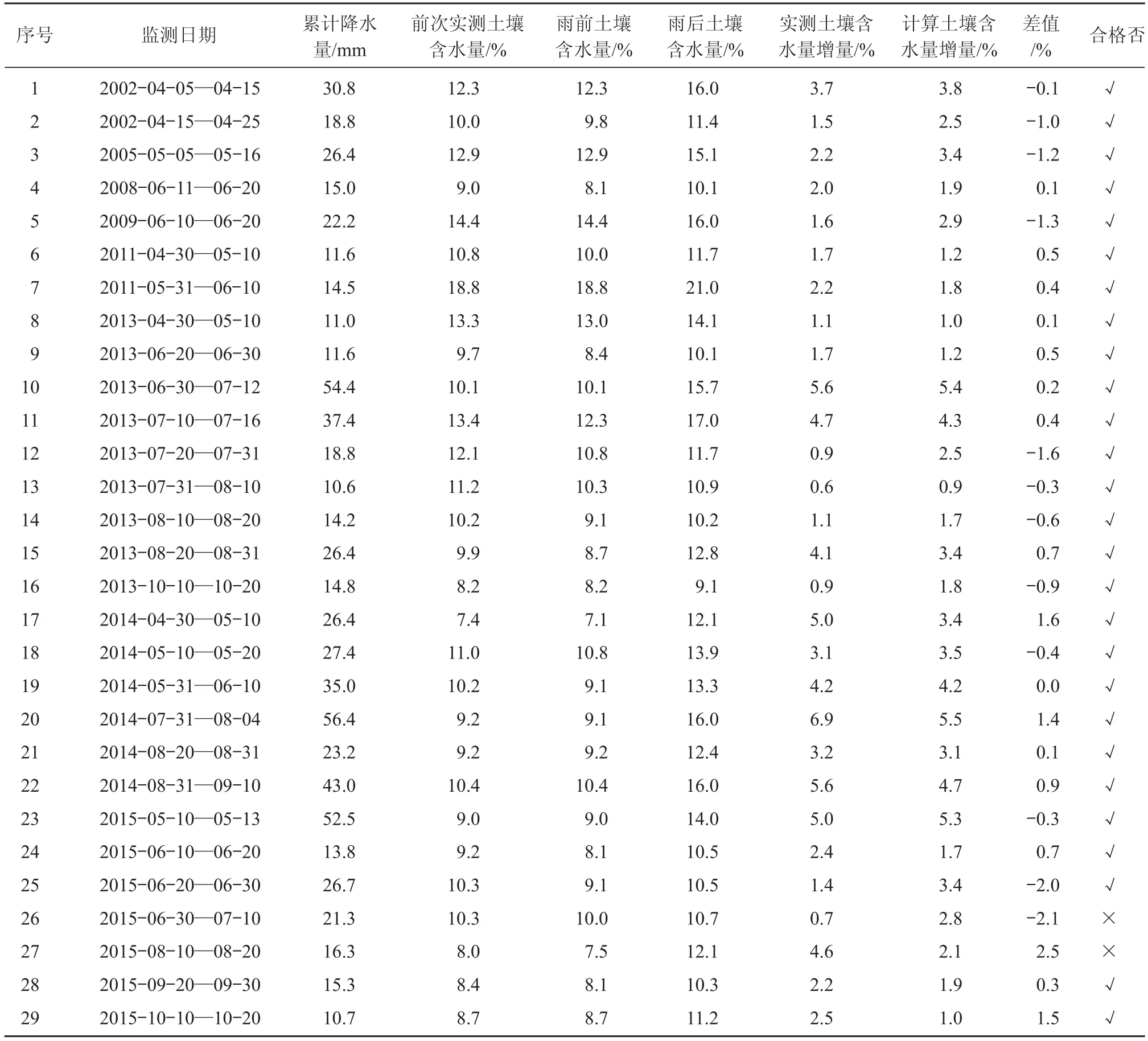
表 2 胡家店站土壤含水量增量计算及增墒曲线拟合精度检验表

2.2.4 拟合精度检验

为检验增墒曲线点距拟合情况，需对本站参加增墒曲线拟合点距进行精度评定。检验精度按实测土壤含水量增量与预测土壤含水量增量差值的绝对值 ≤ 2% 规定控制（视为合格），合格率（合格点距个数与参加检验点距总个数的百分比）≥ 80%，则通过拟合精度检验。经检验，参加胡家店站增墒曲线拟合精度检验共 29 组数据，合格率达 93%。

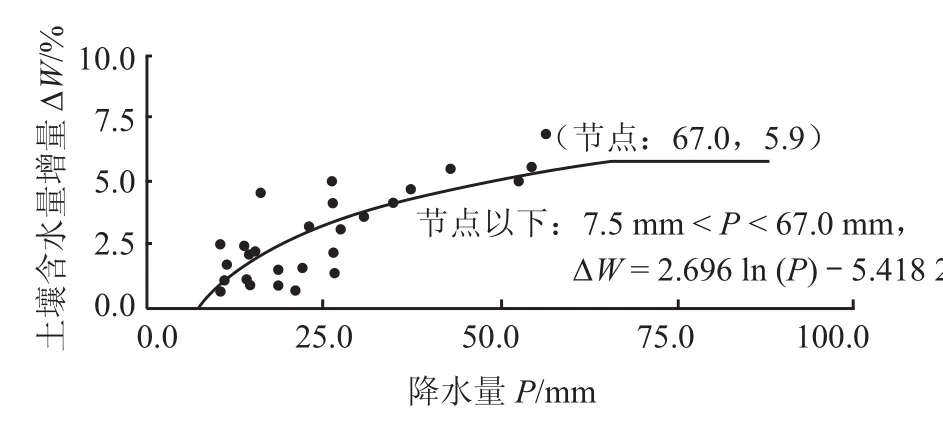
图 2 胡家店站降水量与土壤含水量增量关系图

2.2.5 预测精度检验

选取胡家店墒情站 2016 年 11 组实测墒情数据进行验证（实测数据选取要求：未参加拟合定线，相邻两测次中间发生有效降水）。根据前后 2 次实测土壤含水量及无雨时间间隔，利用退墒模型推算出降水前一日（雨前）和降水后一日（雨后）2 次土壤含水量（如果雨前、雨后有实测土壤含水量则不需进行退墒模型推算），二者差值即为实测土壤含水量增量。根据实测降水量、雨前土壤含水量，利用增墒公式计算出土壤含水量增量（预测值），该值与实测土壤含水量增量差值的绝对值 ≤ 2%，则视为合格。

经检验，11 组数据中有 9 组数据检验合格，合格率为 82%，可以应用到生产预测。

3 预测模型应用

已知 2017 年 5 月 10 日 8 时监测的胡家店站实测土壤含水量为 9.0%，监测到 5 月 12 日降水量为10.0 mm，应用时利用预测模型预测 5 月 15 日 8 时的土壤含水量。胡家店站增墒、退墒关系式如表 3所示。

表 3 胡家店站增墒、退墒关系式表

采用先退墒、后增墒、再退墒的办法进行预测。退墒时段分为两段，分别为：5 月 10—11 日，5 月 13—15 日；增墒时段为 5 月 12 日。

首先计算出 5 月 12 日 8 时雨前土壤含水量。由于 5 月 10 日 8 时实测土壤含水量为 9.0%，＜ 12.8%，选用该站节点以下退墒公式，即 y = 15.034 e-0.016x。当 y1= 9.0% 时，计算连续无雨日数（初始值）x1=32.1 d。5 月 10 日 8 时到 12 日 8 时无雨，对应连续无雨日数为 2 d，即至 5 月 12 日 8 时，累计连续无雨日数 x2= 34.1 d，计算 5月 12 日 8 时土壤含水量（雨前）y2= 8.7%。

5 月 12 日实测降水为 10.0 mm，＜ 67.0 mm，应选用增墒公式 ∆W = 2.696 ln（P）- 5.418 2。当 P =10.0 mm 时，计算土壤含水量增量为 ∆W = 0.8%，则5 月 13 日 8 时土壤含水量（雨后）y2+ ∆W = 8.7% +0.8% = 9.5%；再应用退墒公式 y = 15.034 e-0.016x，计算 3 d 后即 5 月 15 日 8 时土壤含水量为 9.1%。5 月15 日 8 时实测土壤含水量为 10.3%，预报差值为9.1% -10.3% = -1.2%，符合 SL 364—2015《土壤墒情监测规范》规定的 ± 2% 精度要求。土壤含水量预测成果如表 4 所示。

表 4 土壤含水量预测成果表

4 结语

基于水量平衡法建立的土壤含水量预测模型，因果关系清楚，理论依据充分，建模简单，预测精度较好，适合影响因素较集中（如降水、蒸散发、前期土湿）的墒情站创建预测模型。预测模型在实际应用过程中，会有增墒、退墒交替出现，应用起来较为繁琐。为了方便应用，可将本方法创建的增墒、退墒关系式进行数值化处理，并开发成计算机应用软件，实现在计算机平台上预测。预见期内如发生大强度降水或监测地块灌溉等特殊情况，不宜用本模型进行土壤含水量预测。本模型是在多年实测水文资料基础上创建的，模型具有明显的地域属性。但是，对于土壤质地、气象和下垫面等条件相似的墒情站可移用。对于影响因素较多（如降水、蒸散发、风力、温度、前期土湿等），影响力均衡且显著的墒情站，建议采用多影响因子预测模型（如多元回归、人工神经网络 BP 等预测模型）进行土壤含水量预测。