提高多重线性回归分析实践技能的实证分析
罗文海,张庆凤
(1.滨州医学院烟台校区,山东 烟台 264003;2.烟台毓璜顶医院,山东 烟台 264003)
多重线性回归是常用的统计分析方法,然而在多重线性回归分析中有时会出现一些问题,如由于多重线性回归的实践技能不强,致使多重线性回归分析的结论不够准确和合理。因此,应当不断增强多重线性回归分析的实践技能,以获得更加准确和合理的统计分析结果。
1 多重线性回归分析的习惯做法
许多人在进行多重线性回归分析时,有习惯做法,以案例1进行说明。案例1:随机抽取27名糖尿病病人的血清总胆固醇(mmol/L)、甘油三酯(mmol/L)、空腹胰岛素(μU/ml)、糖化血红蛋白(%)、空腹血糖(mmol/L)的测量值(见表1),试分析血糖的影响因素。
以血糖作为因变量y,血清总胆固醇、甘油三酯、空腹胰岛素、糖化血红蛋白作为自变量 X1、X2、X3、X4。逐步法是多重线性回归分析的常用方法,采用软件SPSS19.0进行统计,取检验水准的默认值α入=0.05、α出=0.10,逐步法的模型检验有统计学意义(P<0.001),其偏回归系数及其检验结果见表2。
由表2可见,按α=0.05的水准,只有X4和X1被选入多重线性回归方程,这是许多人习惯做法的结果。从专业知识上讲,空腹胰岛素是公认的能够对血糖产生重要影响的因素,为何没有被选入回归方程?而在专业上认为对血糖没有重要影响的血清总胆固醇却为何被选入回归方程?因此,该结果不够合理,应该进一步探讨其原因。
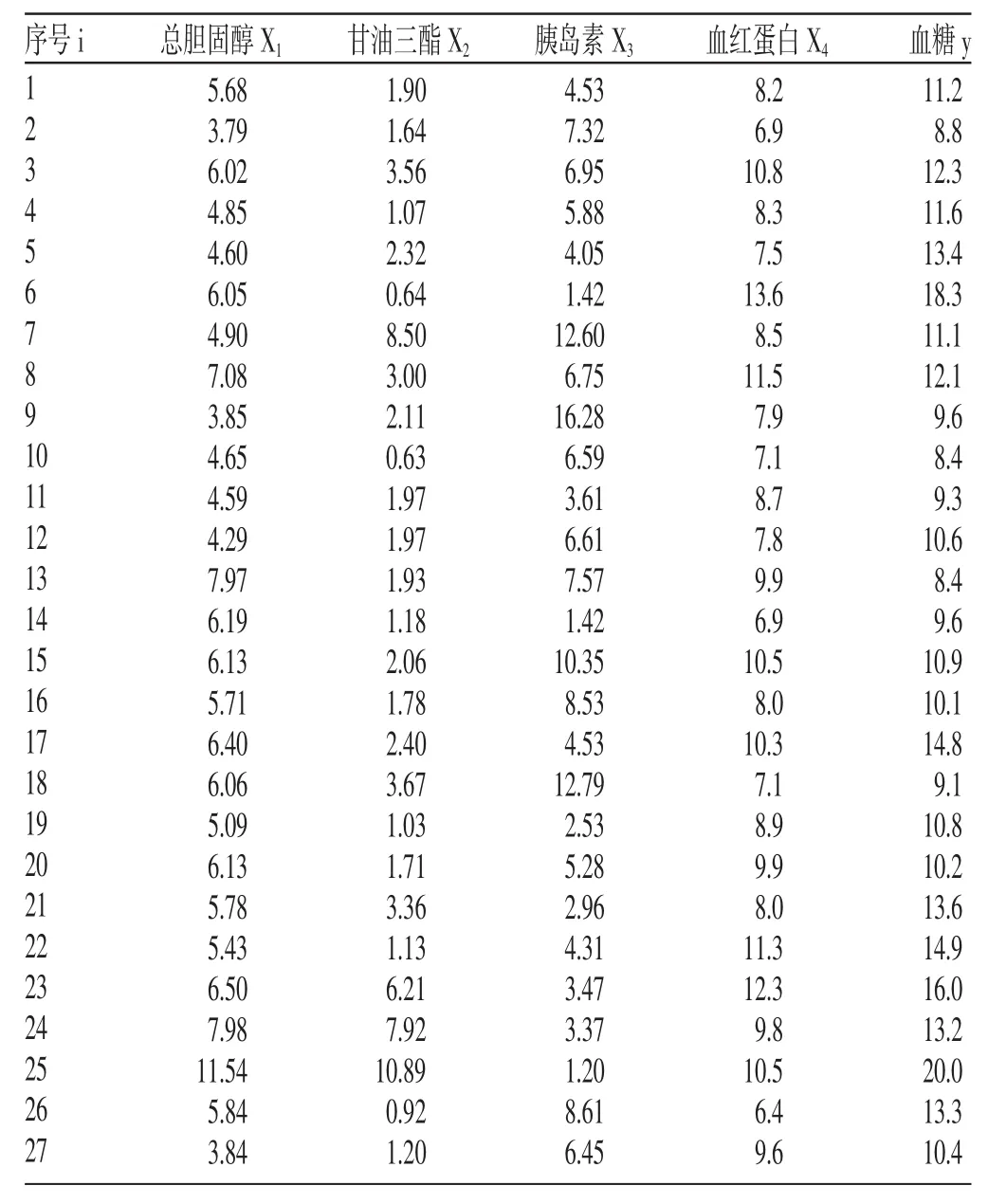
表1 27名糖尿病病人的血糖及有关变量测量结果

表2 逐步法偏回归系数估计及其检验结果
2 多重线性回归分析的常见问题
使用多重线性回归模型需要一定的前提条件,其前提条件包括多个自变量之间无多重共线性。使用多重线性回归分析的常见问题是不重视审查多重线性回归分析的前提条件,从而导致许多问题,甚至会导致错误的分析结果和结论。如可以导致专业上认为非常重要的自变量无统计学意义而不能进入方程;偏回归系数估计值大小或符号与专业知识不符;自变量对因变量作用的实际意义难以解释,有悖常识而产生悖论。
3 多重线性回归分析的高级技能分析
为了便于评价上述逐步法的结果,给出强制法全模型的结果。取检验水准的默认值α入=0.05、α出=0.10。强制法模型检验有统计学意义(P<0.001),说明4个自变量对血糖有作用。其偏回归系数及检验结果见表3。
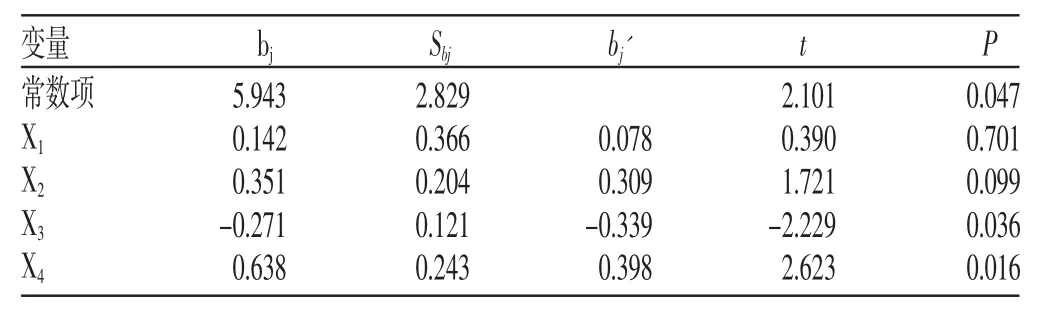
表3 强制法偏回归系数估计及其检验
由表3可见,按α=0.05水准,强制法的结果只有X3、X4有统计学意义(P<0.05),而 X1、X2均无统计学意义(P>0.05)。从标准化偏回归系数 bj'绝对值可见,X4、X3、X2、X1对因变量 y的作用依次减小。X1对因变量y的作用最小,这与专业解释的血清总胆固醇X1不是对血糖有重要影响的因素相吻合,说明上述逐步法的结果将X1选入多重线性回归方程不合理。
导致多重线性回归分析结论不合理的常见原因是自变量多重共线性所致。上述逐步法的不合理结论可能是由于自变量多重共线性所致[1],现试着进行分析。
3.1 自变量多重共线性诊断
案例1的自变量多重共线性诊断结果见表4。

表4 案例1多重共线性诊断结果
在表4中第4、第5维度的条件指数均大于10,第4维度含有方差分量>0.5的自变量X1和X4,因此认为多重共线性严重存在[2]。有多重共线性严重存在,因此可能导致在逐步法结果中对y作用比较大的X3不能被选入而对y作用最小的X1反而被选入模型的不合理情况。为了消除多重共线性的影响,需要先确定主要的多重共线性变量,分别从一个自变量与另一个自变量的简单相关系数rx、一个自变量与其他自变量的决定系数R2和校正决定系数R2adj进行分析[3],结果见表5~8。注:*为P<0.01
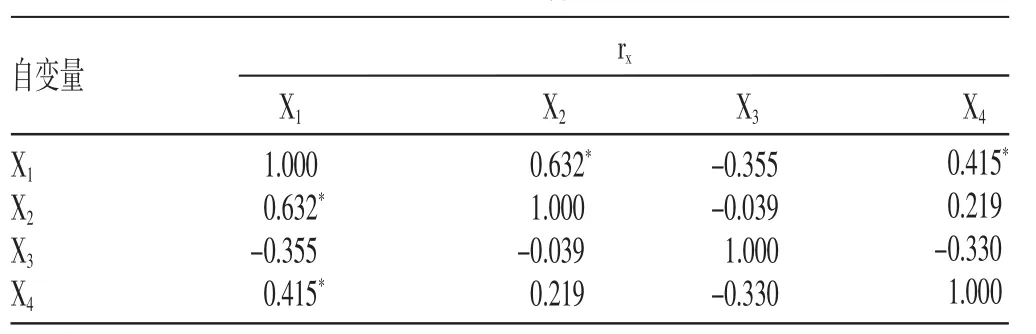
表5 主要多重共线性变量分析1
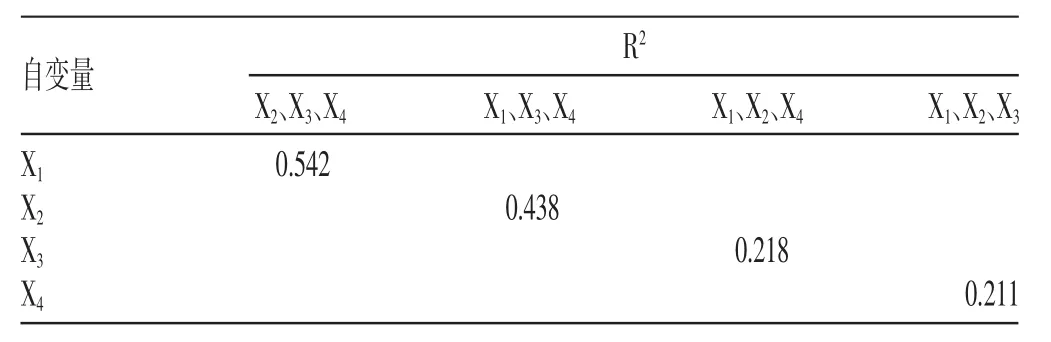
表6 主要多重共线性变量分析2

表7 主要多重共线性变量分析3
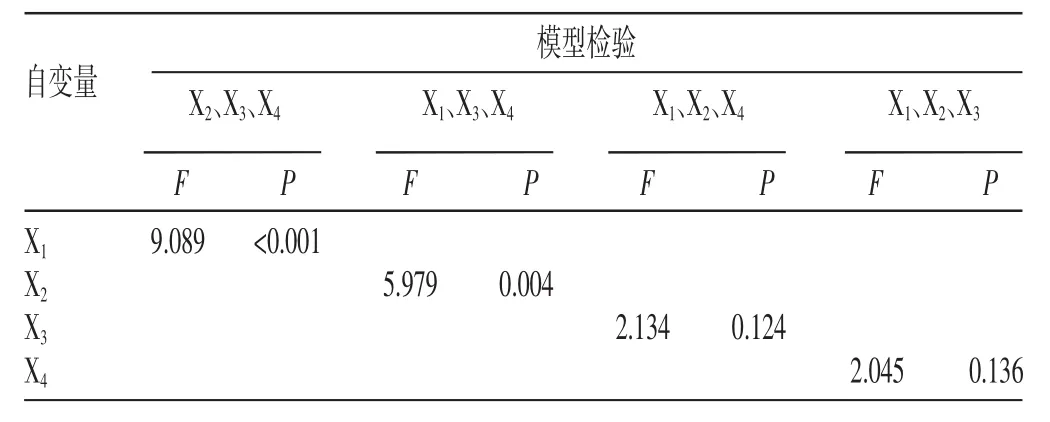
表8 主要多重共线性变量分析4
表 5~8 表明,从 rx、R2、R2adj、假设检验的 F、P 值几个方面均说明 X1与 X2、X3、X4的多重线性回归关系比 X2与 X1、X3、X4,X3与 X1、X2、X4,X4与 X1、X2、X3的多重线性回归关系更强,提示X1与X2、X3、X4的多重共线性最强。在表4中X1对应的VIF和方差分量最大(0.74),并达到了多重共线性严重存在的程度,也提示X1与X2、X3、X4的多重共线性最强。因此,X1是导致多重共线性的主要变量。
3.2 自变量多重共线性处理
3.2.1 删掉主要多重共线性变量 当自变量多重共线性严重存在时,常见的处理方法是删掉导致多重共线性的变量,因此案例1应当删掉X1。删掉X1的逐步法回归模型检验有统计学意义(P<0.001),说明甘油三酯、空腹胰岛素和糖化血红蛋白对血糖有作用。删掉X1逐步法的偏回归系数及其检验结果见表9。
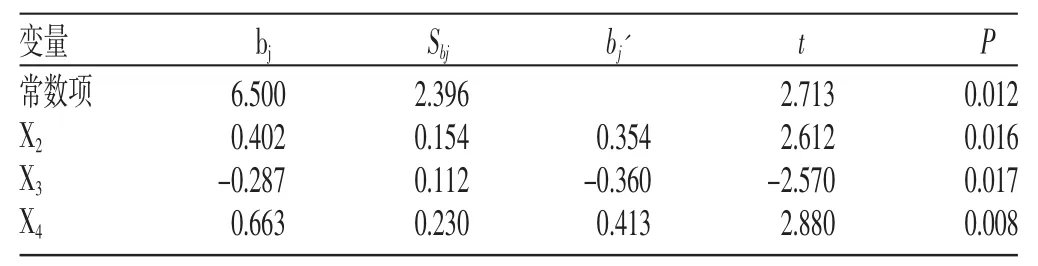
表9 删掉X1逐步法偏回归系数估计及其检验
由表9可见,删掉X1逐步法的X2、X3、X4偏回归系数均有统计学意义(P<0.05),从标准化偏回归系数bj'绝对值可见,X4、X3、X2对因变量y的作用依次减小。对血糖有重要影响的空腹胰岛素等因素均被选入回归模型,符合专业解释,该分析结果和结论合理。这样就消除了在保留X1时对血糖有重要影响的空腹胰岛素未被选入而对血糖没有重要影响的血清总胆固醇反而被选入回归模型的不合理情形。
删掉X1的逐步法结果与含有4个自变量时的强制法、逐步法结果比较见表10(均取默认值α入=0.05,α出=0.10)。
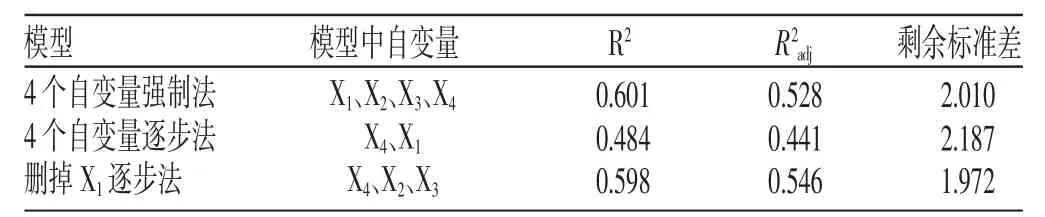
表10 删掉X1逐步法结果与含有4个自变量时的强制法、逐步法结果比较
在表10中,因全模型含有无统计学意义的X1、X2,一般不会选用。通常逐步法能够弥补向前法和向后法的不足,其结果常被选用。但是案例1由于自变量多重共线性的影响,使得4个自变量的逐步法结果R2adj比全模型小、剩余标准差比全模型大,说明回归效果比较差,该模型不满意而不宜采用[4]。而删去X1逐步法的结果R2adj比全模型和4个自变量逐步法模型均大、剩余标准差比全模型和4个自变量逐步法模型均小,说明删去X1逐步法回归效果比较合理,模型比较满意,应该采用。
3.2.2 岭回归分析 当自变量多重共线性严重存在时另一种常见处理方法是岭回归分析。岭回归是处理多重共线性比较的专用方法,尤其是当多重线性回归分析结果不合乎专业解释时,岭回归分析常能给出比较合理的结果[5]。
案例 2:现测得 22例胎儿的身长(cm)、头围(cm)、体重(g)和胎儿的受精周龄[4]。多重线性回归分析主要结果见表11。
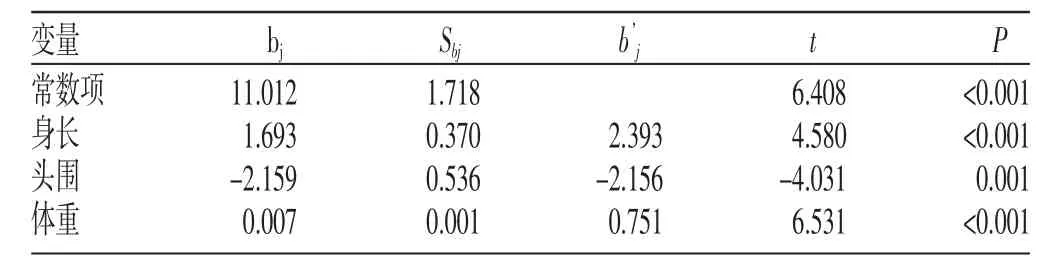
表11 22例胎儿受精周龄影响因素分析
表11表明,头围与受精周龄呈负相关关系,有统计学意义(P<0.01),这显然有悖医学常识。分析其原因,是由于自变量身长、头围、体重的多重共线性所致。经岭回归分析得到的多重线性回归方程为=8.836+0.220身长+0.111头围+0.005体重。可见,头围的回归系数已由原来的负值转化为正值,这符合医学常识,回归分析结果比较合理。案例1当删去X1后在α入=0.05,α出=0.10的水准下逐步法的回归方程为:=6.500+0.402X2-0.287X3+0.663X4;而相应岭回归方程为:=7.817+0.291X2-0.213X3+0.504X4。同样说明了岭回归方法能够使多重线性回归的回归系数发生改变,从而有利于获得符合专业解释的结果。
综上所述,在进行多重线性回归分析时,应当做多重线性回归分析前提条件的判定分析。若判定分析的结果是所分析数据的特征不符合多重线性回归分析前提条件,则必须采用多重线性回归分析的高级技术才能得出正确的分析结论。如案例1的习惯性分析没有将重要变量空腹胰岛素X3选入回归方程,而是将不太重要的变量血清总胆固醇X1选入回归模型,而运用自变量多重共线性诊断技术、确定主要共线性自变量技术和消除自变量多重共线性的删除主要共线性自变量技术,才得到了符合专业解释的合理结果和结论。只有具备良好的实践技能,才能拥有更强的创新能力[6]。因此,与其他良好的实践技能一样[7-8],培养和提高多重线性回归分析的高级技能,对于及时、准确发现科研和管理领域的内在规律具有十分重要的意义。
——以多重共线性内容为例

