基于铁岭市水资源价值评价研究
(辽宁省铁岭水文局,辽宁 铁岭 112000)
在社会经济、水资源以及生态系统这个大体系探讨水资源价值对于规避水资源需求过度膨胀、城市水价科学管理具有重要意义。为最大限度地提高水资源综合效益,提高利用效率并准确定量地分析城市水资源的提升空间,探讨水资源潜在的应用价值,国内外学者分别从多个角度提出了不同的评价方法并在各个社会领域、水利行业,以及水资源价值评价等方面得到了广泛的应用和推广。目前所运用的主要理论有专家测度原理、运筹学理论、数理统计理论、模糊数学理论以及智能理论等,如姜文来[1]等基于水资源价值评价方法和理论构建了相应的评价模型;韦林均[2]等对各评价指标的权重利用模糊层次分析法进行确定,从而构建了基于模糊层次分析理论的灰色评价模型并将其应用于水资源价值评价;张国珍[3]等以兰州市为例利用模糊评价法评价了研究区域水资源价值;董胜男[4]等结合区域地理特征和水资源系统内涵构建了指标体系并利用模糊可变模型进行了综合的研究分析。然而,在水资源价值评价过程中利用可变模糊集法其核心内容是科学、合理、客观地确定指标权重,不同的确定方法可显著影响评价结果的有效性与精确度。因此,针对目前在可变模糊综合评价中指标权重、距离参数以及平方准则确定过程中存在主观性判断的问题,为减少人为因素对评价结果的不利影响,本文在详细分析了模糊优选理论及求解过程的基础上进行了深入的探讨分析,利用神经网络的自学习功能将网络的结构进行调整以替代传统的专家打分法确定指标权重,然后以铁岭市为例利用模型评价了其水资源价值,通过对比分析可变模糊集法评价结果验证了模型的适应性与准确性。
1 构建模糊优选神经网络模型
1.1 神经网络与模糊优选模型
随着科技的进步和发展,人工神经网络因具有自适应学习和非线性映射等特性得到快速的发展和应用,它是一种属于工程性系统可通过识别理解并模拟大脑组织结构而形成的一种智能模拟方法。人工神经网络法建立在数学(数值分析、线性规划)、统计学(编码、统计计算)以及信息处理(压缩、编码、密码)等学科领域的基础上,具有记忆、学习、计算以及智能处理功能,可利用神经元逼近至任意分线性作用函数并被广泛应用于模式识别、经济管理以及优化控制等领域[5]。
考虑到多数情况下客观事物本身尚不存在统一的、公认的判定标准,为便于计算并提高决策效果相关专家给出了模糊优选模型,对于模型参数为α=2、p=1时其激励函数模型表达式如下:
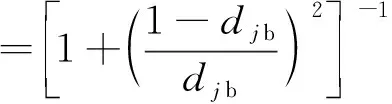
(1)
式中wi——各指标的权向量;
rij——样本j的第i个指标特征值对识别模糊概念A的相对隶属度;
djg、djb——待评价样本j对应于优、劣广义海明权的距离。
因未形成统一、标准的主观定权理论方法,因此,在指标权重确定过程中很难避免因主观意识不一致造成权重结果存在一定差异的现象,为提高指标权重的客观性文中利用神经网络模型的自学习能力进行计算并建立模糊优选神经网络模型。结合陈守煜等提出的神经网络激励函数相关参数及特征,以3层次结构形式即输入层、隐含层和输出层为模糊优选神经网络模型结构类型,对综合评价值V可利用所构建模型进行确定,在各评价等级上水资源价值的隶属度即为评价结果。
为更加客观、准确地反映水资源综合价值,在求得水资源综合评价值V时利用下式进行模糊综合指数的转化:
W=V·T
(2)
式中W——水资源价值模糊综合评价指数;
V、T——水资源价值综合评价值和评价等级向量。
水资源价值模糊综合评价指数不仅可反映影响水资源价值的诸多因素,而且可将不同层次的各影响因素结合起来客观反映水资源现状,其取值范围小于最大级别并大于1。综合指数值的大小代表了水资源价值的高低,值越小则水资源价值越高;值越高相应的水资源价值就越小。
1.2 建模方法及流程
以3层拓扑体系作为模糊优选网络模型结构,其中输入层和输出层分别为评价指标以及水资源价值等级标准。引入评价对象X的指标特征为m,相应的特征值向量可表示为X=(x1,x2,…,xm)=xi。利用c个级别和m个指标可构建标准区间矩阵如下:
(3)
建模及评价过程如下:
a. 利用指标等级标准相邻两侧区间的上、下限值确定Icd,公式如下:
(4)
式中Icd——指标区间值矩阵。
b. 结合各指标的实际情况和上述公式可确定对应于等级h时指标i的M矩阵,公式如下:
(5)
(6)
c. 利用矩阵M、Icd、Iab以及相对差异函数公式可确定指标相对隶属度矩阵。假定吸引域X区间[a,b]中的一点为M,而x为落入区间范围内的任意点,则x落入M点左侧和右侧时DA(u)可分别采用下述公式:
(7)
(8)
式中,β值为1并符合差异函数相关标准和要求。然后利用上述结果可确定相对隶属度μA(u),其表达式如下:
(9)
针对x值不落入区间[c,d]的情况,相应的DA(u)为-1,μA(u)ih为0,其相对隶属度矩阵μA(u)如下:
(10)

d. 模型神经元个数的选取。结合评价指标具体内涵和特征可将输入层神经元确定为5个,然后根据水资源价值各等级标准确定模型输出层单元个数为1个。可通过下述公式确定模型隐含层神经元个数:
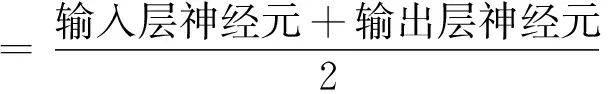
隐含层神经元=(输入层神经元+输出层神经元)1/2
利用上述分析结果和公式最终可确定隐含层元素为3个,因此在3层次神经网络拓扑结构中输入层、输出层以及隐含层的神经元个数分别为5个、1个、3个。原始数据作为输出层初始数据,据此可利用模型进行水资源价值估算。
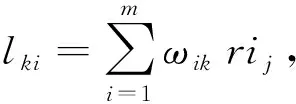
(11)
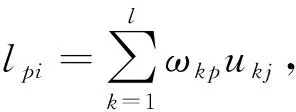
(12)
模糊优选网络模型的权重调整系数计算利用相关文献中的基本公式,对于隐含层与输出层的节点k、p之间的权重调整量采用下式计算:
(13)
式中η——指标学习效率系数;
M(upj)——样本j所期望的输出结果。
输入层与隐含层的节点i、k之间的权重调整量采用下式计算:
(14)
(15)
2 实例应用
2.1 评价指标的选取
本文结合已有研究成果和铁岭市水资源价值实际状况,在遵循科学性、代表性、可获取性、合理性的基础上筛选出5项典型的指标,即X1~X5,分别代表水质、人均水资源量、人均GDP、万元GDP用水量以及人口密度。根据铁岭市水资源公报提供的有关数据对水质综合指数进行计算和求解,结合人均GDP调查数据结果得到人均国民生产总值标准;利用相关学者提出的水紧缺指标确定人均水资源量标准;根据全国人口统计相关数据等级划分结果确定人口密度标准值[6]。铁岭市水资源价值各项指标统计值及评价标准见表1。
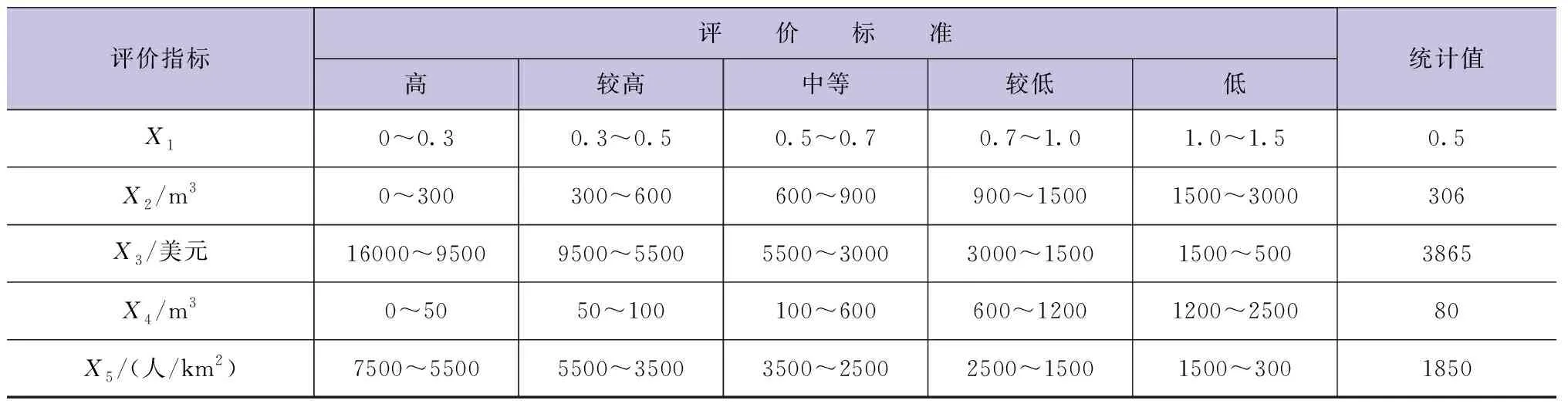
表1 铁岭市水资源价值指标统计值及评价标准
2.2 评价结果分析
根据待评价样本的特征值向量进行归一化处理,并按照文中所述公式可得到相对隶属度矩阵,对网络结构利用生成的样本进行训练(结果见表2)。然后通过运行求解得到模型输出层结果为2.54。对铁岭市水资源价值利用可变模糊集进行评价(结果见表3)。研究表明:对铁岭市水资源价值分别采用可变模糊集方法和模糊优选神经网络进行评价,其评价结果保持良好的一致性,水资源价值等级处于中等与较高水平区间,由此表明铁岭市仍具有一定的水资源价值提升空间[7-8]。

表2 网络模型对各等级区间的权重训练结果

表3 铁岭市水资源价值不同模型评价结果
3 结 论
综合考虑各种影响因素对水资源价值进行评价,不仅可以综合评定水资源的实际状况,而且可为城市水价的科学管理提供一定决策依据和参考。本文以铁岭市为例,利用模糊优选神经网络进行实例研究,并将其评价结果与可变模糊集进行对比分析,得出的主要结论如下:
a.结合铁岭市水资源特点构建了包含水质、人均GDP、万元GDP用水量、人均水资源量、人口密度5项指标的指标体系,所选取的评价指标具有典型的代表性,能够涵盖研究区域水资源价值的各个方面。
b.对评价模型的各层指标权重利用客观权重法进行计算,可有效避免由于主观随意性判断对评价结果造成的误差。对铁岭市水资源价值利用模型进行了评价分析,结果表明评价结果能较好地反映研究区域水资源价值真实状况。
c. 在详细分析了模糊优选和神经网络理论方法、计算流程的基础上构建了评价模型,以铁岭市为例采用两种不同模型进行评价,并对比分析了评价结果。其评价结果保持良好的一致性,水资源价值等级处于中等与较高水平区间,铁岭市仍具有一定的水资源价值提升空间。

