双曲空间下国际贸易网络建模与分析
——以小麦国际贸易为例
吴宗柠,吕俊宇,蔡宏波,樊 瑛
(北京师范大学a.系统科学学院;b.经济与工商管理学院,北京 100875)
0 引言
复杂网络作为复杂系统与复杂性科学重要的研究工具与范式一经提出,就被广泛应用在各个领域。经济系统是典型的复杂系统,而国际贸易是经济系统的重要组成部分,基于统计物理与复杂网络理论,研究国际贸易的拓扑结构和演化特征,有助于从有限的数据中挖掘重要的贸易情报。2003年,Serrano等学者[1]实证发现国际贸易网络同样具有“小世界”、“无标度”以及高集聚性等网络特性,即随机网络不能很好反映国际贸易真实的网络特性,由此揭开了国际贸易网络研究的序幕。许多学者利用这一研究思路,从网络属性与经济周期性之间的关系[2]、国际贸易格局[3-5]、国际贸易危机传播[6-7]和网络演化动力学[8-9]等角度展开了大量的研究。
国际贸易网络反映的是网络拓扑结构信息,从网络拓扑信息去挖掘有效距离,对国际贸易双边流量动因探究有着重要意义。国际贸易领域研究贸易距离主要采用地理信息,但贸易距离对贸易流量的影响力逐年减弱[10-11],说明地理距离不能很好反映贸易的有效距离。而网络嵌入的方法可以利用拓扑信息挖掘有效距离[12-13],进而协助我们探究影响双边贸易流量的距离因素。
近年来,相关学者基于双曲几何学提出了一套网络嵌入的方法,可以帮助我们理解复杂网络背后的蕴藏的几何特性。由Amitri Krioukov等人[14]提出了复杂网络的双曲几何学,并建立了研究复杂网络结构与功能的几何框架。研究表明复杂网络双曲模型的度量特性和负曲率可以反映复杂网络异质性和强集聚性,还能将网络结构和距离完美地结合在一起。由于该研究范式具有明确的实际意义和简明的数学形式,进而产生了一系列的研究工作[15-17]。文献[17]最早将该方法引入国际贸易领域,利用双曲空间中的距离度量刻画了国际贸易有效距离。
为了同时考虑国家经济规模与贸易距离两大因素在国际贸易中的作用,基于国际小麦贸易数据和复杂网络几何测度的理论与方法,重构了国际小麦贸易网络,进而探究小麦国际贸易蕴藏的几何特性。本文旨在复杂网络双曲几何视角下运用新的骨架网络的提取方法生成原始贸易网络,并在此基础上挖掘双曲空间中的几何测度的经济学意义以及国家地位演化规律。
1 数据来源与骨架网络
1.1 数据来源与处理
国际贸易数据主要来自于联合国商品贸易统计数据库,该数据库是由联合国统计署创建并涵盖了全球99%的商品交易。本文在贸易数据库中选取了1995年到2015年的数据作为分析的对象,数据主要由贸易国家(地区)、贸易额、年份以及补充数量所组成。经过数据预处理,最终选取了162个国家(地区)作为研究对象。
1.2 国际贸易骨架网络
国际贸易网络拓扑信息有助于对贸易关系结构、演化的理解。国际贸易是个复杂系统,它的微观结构和演化特性都非常复杂,但从实际意义分析,贸易流量较小的链路对国际贸易全局的影响力不大。因此,我们可以利用这一特点提取国际贸易骨架网络,进而协助我们更好地分析国际贸易系统的结构特征和演化规律。在国际贸易领域常用的提取骨架网络方法有:最小生成树[18]、局部概率骨架网络[17]抽取等方法。
本文结合上述方法的优势,修正了国际贸易骨架网络抽取的方法,抽取的基本思想是:首先根据贸易流量的大小进行降序排序,然后从后往前依次删去贸易额最小的链路,这里在删除链路边的时候,若原始网络节点变为孤立点时,该节点也予以删除。选取合适的阈值就能得到国际贸易骨架网络。由于阈值的选取方法对结果影响重大,我们最后还对阈值的选取做了进一步的约束。数据处理过程中,以当前边数与原始边数的比例(LB/L0)作为横轴,当前节点数与原始节点数的比例(NB/N0)作为纵轴的图形L中(如图1),随着链路的减少,节点数会在某一阈值后迅速减少,节点的相变点骨架网络选取的合理阈值[19],即图1中五角星所在的位置。这样能保障保留原始小麦贸易网络绝大多数的节点而尽可能剔除影响力小的边。纵观1995年至2015年的国际小麦贸易骨架网络阈值,如表1所示,结果发现其逐渐偏离于对角线,说明随着时间的变化,贸易关系显著的国家数变多,小麦贸易一体化趋势愈发显著。此外,2005年到2015年间,阈值曲线基本重叠在一起,说明小麦贸易网络结构趋于稳定。
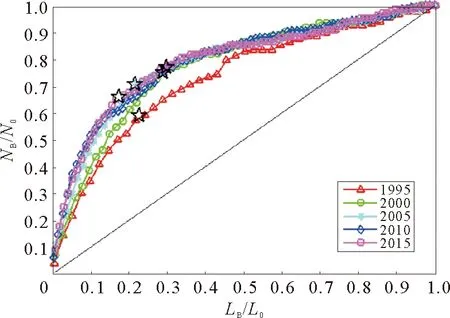
图1 国际小麦贸易骨架网络阈值选取示意图Fig.1 Threshold value of the international wheat trade network
该方法的最大好处在于保留了统计显著的连边,贸易链路大幅减少的同时保证了骨架网络同样具备原始贸易网络的关键特征,即小世界特性、网络异质性和高聚集性。在骨架网络中,节点数占原始网络节点数的66.15%,边数的17.34%,其贸易额占原始网络贸易额的93.43%,骨架网络的平均度为5.81,聚类系数为0.41,这说明骨架网络节点间联系较紧密,网络的连通度较好,是原始网络的重要拓扑结构的集合。
2 国际贸易的双曲网络模型构建
2.1 复杂网络的几何框架
双曲空间是一种各向同性空间,具有负曲率,并且不能被嵌入任何欧式空间中。相关研究表明网络的双曲几何模型与隐藏度量模型是等效的[20]。本文在双曲空间研究方法的基础上,采用更为简单的隐藏度量空间模型,构建复杂网络的双曲空间模型。在隐藏度量模型中,每个节点以坐标(r,θ)嵌入半径为R的庞加莱圆盘上,且由幂律分布获得期望度值κ:
(1)
(2)
(3)
(4)
其中,γ为幂律指数,k为原始贸易网络的平均度,极坐标中的角坐标θ在[0,2π]上随机分配。可以看出κ是网络节点度的隐藏变量,即k(κ)=κ。
定义两个节点的角距离da,ij和双曲距离χij:
da,ij=min(|Δθ|,2π-|Δθ|)
(5)
χij=ri+rj+2ln(da,ij/2)
(6)
复杂网络几何模型的构建是基于有效距离的节点连接机制,即基于双曲距离,定义一对节点i和j的连接概率Pij:
(7)
其中,β为模型的参数。
2.2 国际小麦贸易双曲网络映射
双曲网络几何框架可知,建立国际贸易双曲网络模型的关键在于确定节点内在的隐藏变量和双曲空间的坐标。本文结合García等人[17]和Boguá等人[16]提出的双曲映射方法,建立国际小麦贸易双曲网络模型。贸易网络在隐藏度量模型[20]下,本文从全局参数估计和节点坐标的估计两个方面简要地介绍网络映射过程。
2.2.1 模型全局参数估计

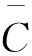
2.2.2 模型节点坐标估计
观测到的真实网络拓扑结构可以通过极大似然估计(MLE)的方法得到双曲空间中的节点坐标,该方法的主要映射思路是贸易网络中国家(节点)的坐标受到网络链接概率的最大化约束,进而得到国家(地区)最佳的坐标。其中似然函数定义为

表1 全局参数估计算法Tab.1 Parameter estimation algorithm
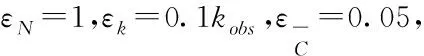

表2 国际小麦贸易骨架网络全局参数估计结果Tab.2 The result on global parameters of the international wheat trade network
(8)
其中,当骨架网络中的节点i,j相连,则aij=1,反之aij=0。
将式(8)处理可得到:
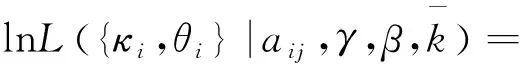
(9)
其中,常数C独立于κi,θi。
1)估计节点径向坐标
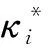
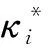
进一步,通过κ-r变换,利用双曲网络节点度的期望值得到节点的径向坐标r,即
(10)
相关研究表明国家GDP和贸易伙伴量有很强的相关关系[1,8],因此双曲模型中的隐藏变量可以衡量国家(地区)的经济规模[17]。
2)估计节点角坐标

(11)
节点角坐标在[0,2π]随机选取,依次访问节点。当节点i被访问时,将移动到使其似然值lnLi最大的角坐标θi上,并在访问其他节点时仍固定在角坐标θi上。实际上,节点移动会导致其他节点的似然值发生变化,但是节点的似然值主要受节点邻居的坐标影响[16]。
3)计算节点间的连接概率pij
为了使重构的双曲贸易网络接近于真实贸易网络,本部分对边的形成加以约束。规定若pij>阈值,则节点连边,反之则不连边,阈值选取标准是让重构双曲网络与骨架网络边数近似相等,进而得到双曲网络上的邻接矩阵。以2015年国际小麦贸易双曲网络为例,其阈值设为0.32,其图像如图2所示。
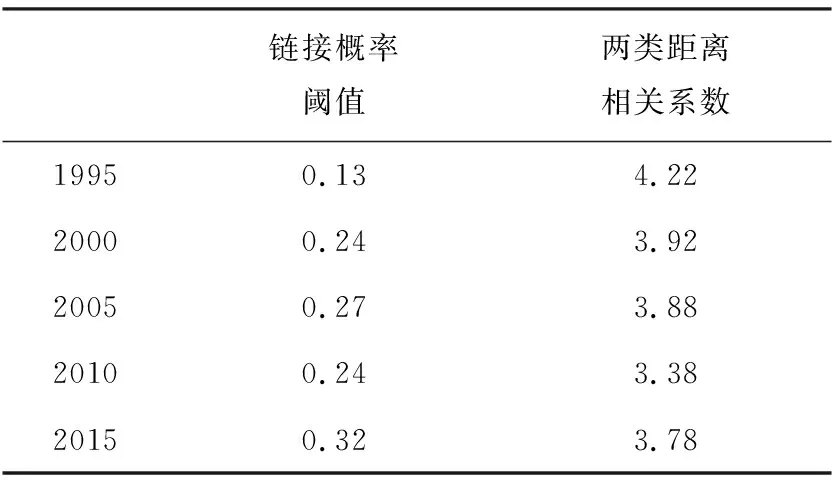
表3 国际小麦贸易双曲网络研究结果Tab.3 The result on the international wheat trade hyperbolic network

图2 2015年国际小麦贸易双曲网络Fig.2 The international wheat trade hyperbolic network in 2015
4)国际贸易双曲网络模型算法检验
为了刻画小麦贸易双曲网络重构的效果,我们采用两种方法检测。首先采用的是评价链路预测方法中最常用的检验方法—AUC,AUC的计算公式为
AUC=(n1+0.5n2)/n
(12)
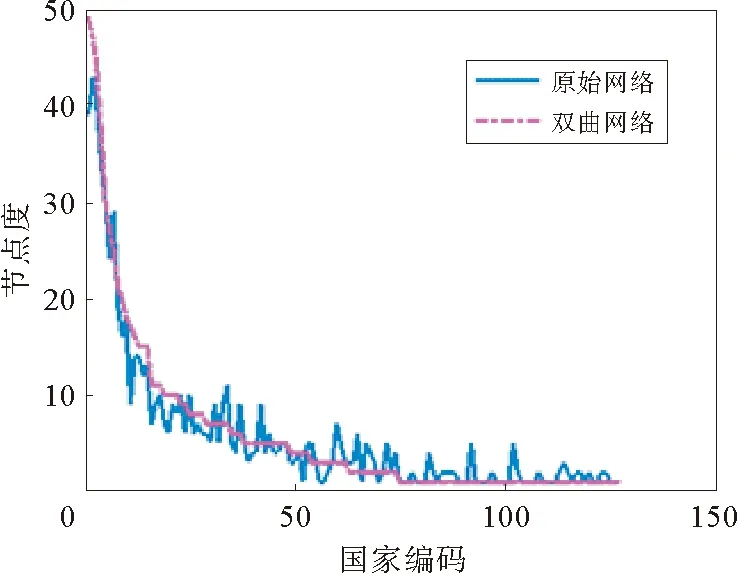
图3 原始网络和双曲网络节点度比较Fig.3 Comparison of node degree between original network and hyperbolic network
其中,n为随机采样的次数,n1和n2分别为测试集内连边的存在可能性评分大于和等于不存在边评分的次数。由式(12)可知,AUC∈[0.5,1]。AUC越大,方法的预测能力越高。在本文中取n=104,通过反复检验,得到本文的双曲映射算法的AUC约为0.95,说明此双曲映射算法的精度较高,双曲映射算法有效。
国际贸易网络中,网络节点度对网络拓扑结构有重要的意义。因此,我们对比了原始网络和双曲网络的度值,如图3,双曲映射算法预测结果比较准确。
3 国际小麦双曲网络特性分析
本文选取了1995年、2000年、2005年、2010年和2015年5个年份的截面数据作为研究对象。结果表明国际小麦贸易双曲网络模型存在“核心-边缘”结构,即在双曲圆盘中,小型经济体总是位于圆盘边缘,而大型经济体则一般位于圆盘中心,如美国、加拿大等。这体现了国际小麦贸易关系具有非均衡性。
双曲空间中的网络测度(极坐标和隐藏变量)同样具有重要意义。文献[14]认为节点间产生连边是由节点的流行性(节点径向测度)和相似性(节点的角距离)决定的,该模型很好地在双曲空间展现了网络的拓扑结构。类似地,在小麦贸易双曲模型中,节点半径可以反映小麦贸易关系建立的容易程度,它的值越小,说明节点越处于圆盘的中心位置,贸易关系的建立就越容易。两个节点间的角距离代表的是节点的相似性,角距离越小说明国家(地区)相似,越容易建立贸易关系。
此外,节点的径坐标(ri,θi)和隐藏变量κ是网络层次结构的粗粒化测度,如图2中对节点期望度坐标赋以颜色进行国家间的层次划分。值得关注的是节点在双曲空间的距离测度可近似为χij=ri+rj+2ln(da,ij/2),然而该双曲距离与地理距离的相关系数同国际贸易网[17]一样都较低,如表3所示,该结果说明贸易的有效距离除了包含地理信息外,还存在其他影响因素,这从贸易拓扑结构的视角印证了地理距离对贸易约束力在减弱。
根据上述分析的结果,我们进一步分析小麦贸易双曲网络的径坐标。双曲网络度中性性排序结果如表3所示,节点径坐标和双曲网络度中性性排序结果的Sperman相关系数为0.876 6,说明双曲网络中的几何性质可以表征网络拓扑结构信息。值得注意的是大部分国家经济增长是以增加贸易关系为前提的[24],因此复杂网络几何模型的径坐标可以作为国家经济增长的测度,这为国际经济增长预测提供了一个新的视角。而从国家排名的角度来看,美国和加拿大处于世界前列,在国际小麦贸易中起到非常重要的作用。联系实际不难发现,在气候、机械化程度、土地资源状况以及国内供求关系等因素影响下,该地区小麦出口量大,在节点重要性排名中占领着核心地位。此外像澳大利亚、俄罗斯、德国和法国等国家,他们的排名波动较大,但都基本处于前五的状态,说明其在国际小麦市场中的作用还是比较显著的。

表4 1995-2015年国际小麦贸易双曲网络度中心性Tab.4 Degree centrality of international wheat trade hyperbolic network in 1995-2015
此外,我们还关注了国家在双曲空间中的发展轨迹,结果如图4所示。1995-2015年间,俄罗斯不断向圆盘中心靠近,它由1995年占圆盘位置的76.81%前进至2015年的41.77%,这说明俄罗斯的农产品贸易越来越好,贸易伙伴变多,这与其现实情况相符。俄罗斯气候适宜,是一个农业大国,是排名仅次于美国、加拿大之后的全球第三大小麦出口国[25]。从1995-2015年俄罗斯的小麦发展情况良好,小麦进出口贸易逐年增长[26],俄罗斯在小麦贸易中具有显著的比较优势,在国际市场占有重要地位,故俄罗斯在国际小麦贸易中的影响力逐渐上升。

图4 双曲空间中国家地位演化图Fig.4 Dynamic evolution of the national status in hyperbolic network
而中国在国际小麦贸易中的影响力呈现逐年下滑的态势,中国在国际小麦贸易双曲网络中由圆盘的中心位置移至圆盘外围位置。我国曾经是世界第一小麦进口大国,近年来随着产业结构的调整,小麦的种植面积正逐年减少,缺乏优质小麦品种,小麦产品的结构性矛盾突出[27]。与进口小麦相比,国产小麦缺乏价格优势,在越来越大的国际竞争压力下,中国在国际小麦贸易的影响力逐年下滑。本文认为我国应着眼于小麦产品的供给侧结构性改革,加快创新小麦科技研发体制,培育优质小麦,建立国产小麦比较优势,才能从根本上解决问题,提高中国在农产品贸易中的地位。此外,中国是贸易大国,但是从骨架网络图中可以看出中国在国际小麦贸易上没有体现其优势,这反映了国际贸易地位在不同产品中具有叠加效应。
4 结论
本文运用复杂网络的双曲几何理论框架,分析了在双曲空间中的国际贸易网络的构建与分析,并以小麦贸易网络为例进行了实证研究。实证结果表明该研究范式的有效性,这套方法可以运用于其他贸易产品空间的映射研究。通过研究我们得出了如下结论:1)随着时间的变化,国际小麦贸易骨架网络中显著的贸易关系逐渐增加,小麦贸易一体化趋势愈发显著;2)双曲空间中国际小麦贸易网络也体现出“核心-边缘”结构;3)国家在双曲空间中位置的演化体现了俄罗斯、中国等贸易大国在国际小麦贸易地位的变迁。

